Таблица 4.1. Классификация принципов управления

а (О - вектора изменения параметров устройства управления;

Р(0 - вектора изменения параметров модели процесса.

Принцип построения устройства управления основан на минимизации некоторых функций разности между желаемой целью и полученным результатом: J (О-3(0 = (О, где ё(0 - ошибка системы, характеризующая абсолютную погрешность в момент времени t.

Погрешность e(t) может использоваться в составе алгоритма управления для замкнутых систем или для оценки качества управления в разомкнутых системах. Сигнал q(t) также может использоваться двояко: для оценки качества системы или для формирования управляющего воздействия.

В табл. 4.1 приведена классификация алгоритмов управления с использованием в качестве признаков введенные выше сигналы.

Анализ таблицы показывает, что часть систем (четыре первые типа) не используют в алгоритме информацию о желаемом значении вектора цели yit), а довольствуются его эквивалентом в виде задающего воздействия g{t). При этом оценка качества q(t) используется лишь для суждения о качестве работы и тем самым носит пассивный характер.

В алгоритме экстремальных систем управления, имеющих своей целью получения экстремума q цель отождествляется с экстремальным значением. В остальных алгоритмах одновременно решаются две задачи: получение оптимальной программы и обеспечение ее вьшолнения.

При выборе принципа управления следует руководствоваться функциями системы и возможностью получения достоверной информации, необходимой для принятия решения и выработки управляющего воздействия. 154

4.2. АЛГОРИТМЫ УПРАВЛЕНИЯ ПАРАМЕТРАМИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

В МПСУ можно выделить преобразования, выполняемые в дискретном времени при реализации алгоритмов в ЭВМ, и преобразования информации, связанные с процессами, происходящими в оборудовании при непрерывном представлении времени. При решении задач управления необходим единый математический аппарат, в качестве которого используются разностные уравнения.

На основании обобщенной модели (см. рис. 4.3) составим структурную схему системы управления (рис. 4.4).

Предположим, что все элементы, указанные на схеме, имеют линейные характеристики, а их описание выполнено с помощью передаточных функций. Отметим передаточные функции элементов, работающих в дискретном времени, и изображение сигналов, представляющих собой решетчатые функции, звездочками. Они характеризуют преобразования, выполняемые в ЭВМ. Передаточные функции на рис. 4.4 характеризуют свойства:

оЬ) - объекта управления;

Wjls), W2is) - измерительных преобразователей у и Ч*; W.{s)-экстраполирующего устройства;

Wti {s), Wtz {s)- алгоритмов преобразования задающего и возмущау<>щего воздействий;

Wi{s) - алгоритма управления;

Wt \s)-желаемого алгоритма функционирования;

Q - алгоритма вычисления критерия качества.

Сигналы, используемые в схеме:

л

у и *F - измеренные значения выходной переменной и

возмущения; л У

л л

-их дискретное представление;

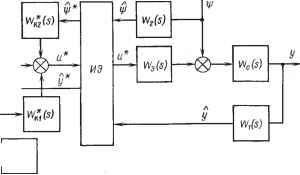Рис. 4.4. Схема системы управления

и*-управляющее воздействие;

е* - ошибка рассогласования замкнутой системы;

у*-желаемое значение выходной переменной.

Пользуясь дискретным преобразованием Лапласа и полагая, что все переменные в описании берутся в дискретные моменты времени, определяемые частотой квантования импульсного элемента (ИЭ), запишем:

[Wo(s)4 (s)]* - Wh (s)[W, (.) У (л)]* , ,

Для воспроизведения без погрешности задающего воздействия g[t) и полного подавления возмущения *F(?) необходимо выполнить условия абсолютной инвариантности:

\ W,[s)W,{s)-\*lW\{s)+WU{s)-\ = \-

[ Wq [s] {s)\ * - Wh [s] [ [s] F {s)\ * = 0.

Поскольку в системе предусмотрены два канала распространения воздействия, то условия абсолютной инвариантности могут быть физически реализованы. При известных характеристиках объекта управления, измерительных преобразователей и алгоритма управления Wsis) можно определить функции Wli(s) и

Условие физической реализуемости функций Wli{s) и iVlzis) требует, чтобы степень полинома числителя была не выше степени полинома знаменателя. Последнее условие в широком диапазоне частот обычно не выполнимо. Однако полученные значения могут быть использованы для оценки желаемого вида преобразования в рабочем диапазоне.

В практике управления параметрами технологического оборудования часто применяют только принцип обратной связи, а элементы с передаточными функциями Wli{s), Wlzis) не используются.

Полагая для схемы рис. 4.4 Wli{s)=Wl2{s) = 0, вычислим дискретное преобразование Лапласа выходной переменной y*{t):

l + Wl{s)[W,(s)iVo(s)W,(s)]* \ + W%(s)[lV,(s)lVo(s)W,{s)y l56

Определим абсолютную погрешность системы: А=;ж {s)-у * {s) = Wl, {s) G* (s)-у* {s) =

\ + Wl(s)[W(s)Wo{s)iV,(s)]* >

Полученное значение A представляет собой полную характеристику погрешности и позволяет рассчитывать показатели качества переходного процесса. Для получения прямой оценки качества, определяемой с помощью показателей: времени регулирования, перерегулирования и установившейся погрешности, необходимо перейти к временным характеристикам погрешности. Расчет временных характеристик зависит от вида экстраполятора, частоты квантования и требований, предъявляемых к точности системы.

Выбор периода квантования. Для преобразования непрерывного сигнала в дискретный МПСУ используют АЦП, в которых выполняется цифровое кван-

тование, включающее в себя как квантование по уровню, так и по времени. Для преобразования цифрового сигнала в непрерывный используются ЦАП и экстраполя-торы.

Если погрешности преобразователей выбраны достаточно малыми, то качество управления существенно зависит от периода квантования. При выборе периода квантования пользуются моделью, структура которой приведена на рис. 4.5, а.

Импульсный элемент (ИЭ) преобразует непрерывный сигнал u{t) в u*{t), который можно представить

uftj

Энстра-полятор

y(t)

ПНЧ

u*(t)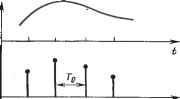

в виде бесконечного

*(0= z и{Щ1-пТ,),

п= - со

где Tq - период квантования; b[t - n Tq)-дельта-функция.

y(t)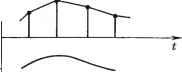

Рис. 4.5. Представление непрерывного сигнала при дискретизации

Последовательное соединение экстраполятора и объекта образует приведенную непрерывную часть (ПНЧ) системы. Задача экстраполятора заключается в преобразовании сигнала между двумя последовательными моментами квантования. Эта задача решается в МПСУ аппаратными средствами.

Применение экстраполяторов призвано решить задачу восстановления непрерывного сигнала по виду решетчатой функции u*{t). В литературе принято называть преобразователи, приводящие к сигналу А'о (г), экстраполяторами нулевого порядка, или фиксаторами, а к x [t) - экстраполяторами первого порядка (рис. 4.5, б). Сигнал на выходе приведенной непрерывной части можно записать, используя импульсную переходную функцию /<: (;-т), следующим образом:

00 оо о, СС

n=-ocO n=-ooO

Выбор периода квантования Tq преследует цель обеспечить восстановление непрерывного сигнала с заданной погрешностью, беря для этого наименьшее число изменений, т. е. увеличивая период квантования. Общие рекомендации по выбору Tq основаны на теореме В. А. Котельникова, согласно которой для воспроизведения сигнала максимальный период квантования Tq не должен превышать Го1/(2/ 1 где Го-период квантования, выбранный на основе теоремы Котельникова; / --максимальная частота в спектре сигнала. В этом случае непрерывный сигнал будет представлен рядом

u,it)= i uinTQlf-jf, (4.1)

где (о, = 2л/ , а дробь, входящая в выражение, носит название функции отсчетов.

Погрешность, получаемая при таком выборе в предположении, что / , неограниченна или достаточно велика, оценивается неравенством

/<--==-1,73

где Е-полная энергия спектра сигнала; -энергия высокочастотной части спектра, т. е. заключенная в полосе частот выше / .

Максимально допустимая величина периода квантования при различных экстраполяторах может быть определена следующим образом.

Пусть непрерывный сигнал u{t) заменен рядом (4.1) с конечным числом членов к. Тогда абсолютная погрешность аппроксимации

Поскольку Го = const, то погрешность можно оценить, пользуясь интерполяционной формулой Ньютона:

Hk = Ho+~{t-to)+{t-to){t-ti)+. ... +

+§it-to)...(t-h-.)+R{t),

где А и-конечные разности п порядка; Wq - значение и при t = tQ; R[t) - остаточный член ряда, который служит оценкой погрешности аппроксимации.

Обозначив разность f + j - г„ = Го = const, п = 0, к и заменив конечные разности производными, запишем

Определим погрешность на интервалах времени между точками квантования, т. е. при 1фпТ^. Обозначим {t - t )/TQ = \ и подставим в (4.2). После преобразований получим

Зададимся условием

R{t) = max\u{t)-u,{t)\, , (4.3)

которое устанавливает требование: максимальное значение абсолютной погрешности на интервалах между точками квантования не должно превышать заданное.

Для усиления неравенства (4.3) подставим в него максимальные значения модуля переменных, т. е.

к

+ °

П v-n

п = 0

<едоп-

Последняя формула является общей. Из нее, задавая значение к, которое соответствует степени аппроксимирующего полинома, описывающего выполняемое зкстраполятором преобразование, можно получить величину Го-

Пример 1. Определить для системы, в которой используется экстраполятор пулевого порядка (см. рис. 4.5, б, Хо(/)).

Так как в этом случае к=0, то max х' 7о<8до , откуда Tg = 8 /max

Пример 2. Определить для системы с экстраполятором первого порядка - линейным (см. рис. 4.5, 6, -\ (t)).

Так как в этом случае к=\, то - То max v(v- 1) <ёдд„, откуда Го = = v88on/max.\- .

Оценим выигрыш от увеличения периода квантования в зависимости от степени воспроизводяшего полинома с помощью коэффициента

Рк - О/с/О'

где Упериод квантования при экстраполяторе к порядка; Го - период квантования при /с = 0. Сопоставим эффективность использования сложных экстраполяторов (табл. 4.2) при различных требованиях к относительной погрешности у системы.

Анализ таблицы показывает, что повышение степени воспроизводящего полинома существенно изменяет период квантования только для прецизионных систем. При удовлетворительной погрешности 5% переход от линейного экстраполятора к квадратичному увеличивает период лишь на 45%, что вряд ли окупится из-за возрастающих аппаратурных затрат. В это же время переход от экстраполятора нулевого уровня к линейному изменит период квантования на порядок.

Типичные алгоритмы управления. Наибольшее распространение в системах управления технологическими параметрами оборудования микроэлектроники нашли линейные законы управления.

В непрерывных системах обычно используются П-, ПИ-, ПИД-законы. Уравнение ПИД-регулятора можно записать так:

cit

Полагая в нем Т^ = 0, получаем ПИ-регулятор, а принимая 7д = 0 и

1 / Г„ = О-П-регулятор.

Если влияние квантования мало, т. е. частота его велика по сравнению с полосой частот непрерывной части системы, выбор

Таблица 4.2. Эффективиосгь экстра1М>лягоров высокого норядка

настраиваемых параметров Г^, и К, выполненный для

непрерывной модели, может быть распространен на дискретный регулятор.

Дискретный ПИД-регулятор можно реализовать в микроЭВМ разными способами. Эти различия связаны с применяемым вычислительным алгоритмом (рекуррентный или нерекуррентный) и принятым методом вычисления интеграла (метод прямоугольников или трапеций). Различные варианты алгоритмов сведены в табл. 4.3. Рекуррентные алгоритмы основаны на вычислении прирагцений, поэтому они характеризуются высоким быстродействием и требуют меньшего объема памяти. Этим и вызвано их более широкое распространение. Замена приращения ошибки системы на выходную переменную обеспечивает уменьшение бросков управляющего воздействия при скачкообразном изменении задания.

Высокое быстродействие ЭВМ дает возможность употреблять при выработке управляющего сигнала несколько замеров выходной переменной. Это используется для усреднения сигналов, что повышает помехоустойчивость системы. Примером таких алгоритмов служит последний алгоритм, приведенный в табл. 4.3.

При существенной частоте квантования выбор параметров настройки регуляторов можно выполнить следующим образом. Запишем алгоритм ПИД-закона в виде дискретной передаточной функции

1-г

Наличие полюса z=l обеспечивает получение .нулевой установившейся ошибки при ступенчатом изменении входного воздействия. Диапазон изменения параметров регулятора должен удовлетворять условиям:

go>0; gi<-go; -{So+Si)<g2<go- (4.5)

Коэффициенты в ПИД-законе связаны с параметрами g следующим образом:

коэффициент передачи K=gQ-g2, коэффициент дифференцирования c=g2/K; коэффициент интегрирования c = {go+gi+g2)/К. Теперь lV-{z) можно представить в виде

Полученный алгоритм управления аналогичен непрерывному ПИД-закону, если выполнены условия (4.5) и Сд>0; с„>0; с„<Сд. Положив в (4.4) g2 = 0 получим

зИ- --гг .

6-2509

Таблица 4.3. Вычислительные алгоритмы ПИД-закоиов

Алгоритмы дискретных ПИД-законов

Особенности реализации

и{к) = К[е{к)+ i e{i-X)+I[e{k)-e[k-\)-\-\

Нерекуррентный, интегрирование методом прямоугольников

u(k) = u{k-\)+ge{k)+g,e{k-\) + g,e(k-2)-

V W V ь Tj To

Рекуррентный, интегрирование методом прямоугольников

и (к) = u(k-l)+goe (к) + g,e{k-l)+ge(k-2);

Рекуррентный, интефирова-ние методом трапеций

О

u(k) = u(k-l)+Kle(k) + e(k-l) + e(k-l)] + +h-y(k)+2y(k-l)-y(k-2)l

u(k)=u(k-\)+K[-y(k)+y(k+l)+-:e(k-l)+ + [-y{k) + 2y{k-l)-y(k-2m

Рекуррентный, с заменой производной ошибки на производную выходной переменной

и {к)=р,и (к-\)+р^и (к - 2)+goe (к) + +g,e(k-l)+g,e(k-2)-

Рекуррентный с улучшенным сглаживанием производной

Pi = So = K

-4б',

\ + 2с[ l-b2ci [l + 2(c, + cJ+c (l+20/2]

2ci-l

\ + 2c

\ + 2ci

ci(2-Ci)-b2C-bO,5ci-l H-2c,

c, = TJTo; с„=Го/Г„; c=TJTo

g2 = K

т. е. ПИ-регулятор. Если при этом положить go = 0, то

Последнее служит алгоритмом И-закона регулирования.

Аналогично можно реализовать П- и ПД-алгоритмы управления.

4.3. АЛГОРИТМЫ УПРАВЛЕНИЯ ПОСЛЕДОВАТЕЛЬНОСТЬЮ ТЕХНОЛОГИЧЕСКОГО ЦИКЛА

Управление последовательностью технологического цикла или состоянием технологического оборудования подразумевает формирование в фиксированные моменты времени дискретных управ-ляюгцих сигналов типа Включить , Выключить , Подать на позицию , Открыть затвор и т. п.

Исходные требования к разрабатываемому управляющему цифровому устройству формулируют обычно в виде словесного описания. Определение структуры устройства, удовлетворяющей этому описанию, подразделяют на две части - абстрактный и структурный синтезы.

В ходе абстрактного синтеза осуществляется переход от словесного описания устройства к формализованному заданию его оператора в виде графов, таблиц, матриц. Сущность задания оператора независимо от его формы состоит в определении перечня входных и выходных переменных устройства и установлении связей между ними.

В процессе структурного синтеза определяется структурная схема устройства. Научной основой этого этапа является аппарат алгебры логики (булевой алгебры), который позволяет перейти к заданию оператора в виде формул и затем упростить последние в соответствии с требованиями к структуре устройства.

В инженерной практике по проектированию управляющих логических устройств промышленной автоматики под логическим синтезом следует понимать процесс составления структурных формул, описывающих схему устройства, по заданным условиям технологического процесса.

Логические функции. Любое логическое выражение, составленное из п двоичных переменных с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую логическую (булеву) функцию п переменных:

F=F{xi, х„),

где F может принимать только два значения: О или 1.