в схеме выполняется условие Y1Y3 - баланса плеч другого моста (его цепь замыкается через очень большие выходную проводимость источника сигнала и выходную проюдимость операционного усилителя), то при Yg= О схема будет иметь коэффициент передачи /Ci5= 1 и очень малую входную проводимость, что позволяет использовать ее в качестве буферного каскада. *

Если в схеме (рис. 5.1) снимать сигнал с узла 6, то коэффициент передачи

Kie= Aie/Aii > (5.36)

будет отличаться от /(15 (5.22) числителем, причем

Aie = A16, £5+0], [3+0] Т P-iAie, (5+0)(4+2), [3+0] + + Н-гАю. [5+0], (3+0) (4+6) + P-sAie, (5+0)(4+2), (3+0)(4+6). (5.37)

Вычисляя аналогично предыдущему входящие в это выражение суммарные алгебраические дополнения

А,б. [5+0]. [3-f 03 = у 9 + П + Vs) {Vs + Y, + Y,) + + F,F , (Y, + Y, + Y, + y, + Y, + Ys) + YYMYi + + Ув) +

+ У..1У..2{У1+У,); Д.6. (5+0) (4+2,: [3+0] = YiYb (Ys + n + - У,У9 (Уг + У, + У в) + + П>вх2(П + У5); (5.38)

А,6. [5+0]. (з+0)(4+б) = УвУ, (У1 + У, + у в) + УвУвх . (Га + Гз); Ai6, (5+0)(4+2), (з+0)(4+б) = YYgY + YzYYg, нетрудно построить с учетом формул (5.24) - (5.30) отношение Ki6= Aie/Aii и выполнить анализ коэффициента передачи /fig.

Р8ссм01ренный пример свидетельствует об эффективности анализа цепей, содержащих интегральные микросхемы, на основе разложения функции цепи по соответствующему параметру.

2. синтез устройств на основе пары преобразований

Соотношения (5.1)-(5.Г0 и (5.6)-(5.9) характеризуют основные свойства линейных электрических цепей. Из них следует, что можно син- тезировать цепь с идеальными активными приборами (6-с ), а затем определить свойства этой же цепи с активными приборами, имеющими конечное значение параметра усиления 6,. и приближенно описывающими сюйства реальных активных приборов.

Представим функцию цепи в виде разложения, например, по усилительному параметру 6 активного прибора

iC(p.e) = A /A = [6 (/7,-e) + L(;7, е)]/[б4/7, e) + L?(/7, е)]. (5.39)

функция цепи с идеальными активными приборами определяется отношением доминирующих полиномов числителя и знаменателя, зависящих только от величин элементов пассивной части цепи;

.......(5.40)

е. lp.e) а^.(е .....(е„)

Такая цепь будет характериьоваться высокой стабильностью и устойчивостью. Поэтому практический интерес представляют схемы, в которых влияние неидеальностей рьальных активных приборов сведено к минимуму. Такую цепь можно описать при помощи идеализированной модели с идеальными активными приборами. Если синтез цепи на идеальных активных приборах выполнен по заданной функции /( (р), определяемой выражением (5.40), то при использовании в этой цепи реальных активных приборов она будет характеризоваться функцией К (р, 0), отличающейся от К (р) остаточными полиномами 6 (/7, 6) и б^р, 6).

Из выражений (5.10)-(5.14) и (5.39), (5.40) следует, что доминирующий полином а характеризует полином числителя и знаменателя функции цепи, в которой включены все идеальные активные приборы (е^.->со). Если включить соответствующее количество активных приборов и найти определитель матрицы полученной цепи, то можно установить вид составных частей остаточного полинома 6 и построить его. Следовательно, выполняя определенные режимы в идеальной цепи (включая или выключая ее активные приборы), можно получить необходимые сведения о свойствах функции такой же цепи, но с реальными Активными приборами.

На основании свойств разложения функции цепи по параметру активного элемента (5.6)-(5.9) можно ввести понятие об эквивалентных преобразованиях и соответствующих им эквивалентных схемах.

Многократное суммарное алгебраическое дополнение Д(В,).....(В„),

характеризующее числитель и знаменатель функции (5.40) цепи с идеальными активными приборами, не изменится, если в нем по определенным правилам [11,12] выполнить взаимную перестановку или перекодирование индексов, обозначающих соответствующие строки и столбцы матрицы проюдимости пассивной части цепи и определяющих узлы подключения активных приборов и внешние узлы цепи. При выполнении этих тождественных матричных преобразований полинома А(е,),(бп) функция (5.40) не изменится, а соответствующие перестановки индексов определят изменения в схеме цепи и приведут к схемам, эквивалентным исходной. Следовательно, эквивалентные цепи характеризуются одинаковым набором элементов,-но различаются конфигурацией схемы. j

Целесообразно построить эквивалентные преобразования, позволяющие непосредственно перейти от даннойреализации к эквивалентной ей. При этом можно не выполнять все этапы синтеза семейства эквивалентных цепей, а получить его при помощи определяемых перекодированием индексов топологических переходов от ранее синтезированной или известной цепи с данной схемной функцией.

Схемы, эквивалентные при использовании в них идеальных активных приборов, €удут приближенно эквивалентны при реальных активных приборах. Числители и знаменатели их функций содержат одинаковые доминирующие полиномы различные остаточные полиномы 6. Поэтому свойства реальных цепей будут отличаться. В частности, они могут иметь различные характеристики устойчивости, чувствительность параметров к изменению величин элементов и другие

свойства, важные при использовании схем. Эквивалентные преобразования позволяют поодной схеме восстановить семейство<схем Данного типа, из которого можно выбрать схему, соответствующую условиям оптимизации.

Одно из эквивалентных преобразований связано с перекодированием индексов подключения выводов активных приборов и определяется тождествами

Ai/г. iv-frw+t). .... (v+m+Di - = Ajz, ig+r)U+i), .... (0+9)(j-f о----=

= Aj/г, iv+na+t).....W+0(O+lh - . , = Уг. {g+r)U+t), . . ., &+g)(0+l), . . . =

- = Ауг, Ig+rHl+t),----W+r)U+th . . . == yz. (g+r)a+t).----W+r)(z+l). . . . =

= уг. (q+r)il+t). .... iy+rKz+t).,. ..= .... (5.41)

При этом Преобразовании происходит перемещение соответствующего вывода активного прибора из одного узла в другой.

Другое эквивалентное преобразование связано с тем, что многократное суммарное алгебраическое дополнение не изменится, если в двух, а в общем случае в любом четном количестве активных приборов, взаимно изменить подключение входных или выходных выводов и в одном из них изменить фазировку входных или выходных выводов. В каком именно зависит от номеров узлов подключения активных приборов схемы, с учетом которых определяется знак суммарного алгебраического дополнения

m+mi+t}.....ii+i)(f+m), , . . = Д(,+)(/+т). .... U+jW+l). =

= А(г+/)(Ж). . . . (g+r)(m+f). .... (5.42)

Для схем, содержащих, например, интегральные микросхемы операционных усилителей напряжения с симметричным (дифференциальным) входом и несимметричным выходом, эквивалентные преобразования индексов f т I + t, I t и i + f q + г, 1- t соответствуют взаимноглу переключению входных или выходных выводов двух операционных усилителей и последующему взаимному переключению входных вьюодов в одном из них.

Другой вид эквивалентных преобразований можно получить при одновременной перестановке и.перекодировании индексов суммарного алгебраического дополнения

\q+r)(l-\-t).....(£Н-Л(г-)-т), ... . = Д(гЧ-/) -Ьт).....{.q+rW+m), ... (5.43)

Функция передачи схемы (рис. 5.1) с идеальными операционными усилителями описывается отношением соответствующих суммарных алгебраических дополнений (5.22). На основании преобразований (5.41)-(5.43) можно записать следующие тождественные выражения:

15. (5-bC)(4-h2). (3-Ь0)(4-Ь6) 15. (Б-Ь0)(4Н-2). (ЗН-0)(2-Ь6) 11. (5-f-0)(4-f-2), (3-f-0)(4-f-6) - \\, (S-f0)(4-f-2), (3-1-0)(2+6) IS. (S-bO)(6-b2), (3-ЬЦ)(4-Ь6)

(5.44)

n, ib+m+i). (3-f-0)(4-f-6) Д- 15, (5-f0)(4-f-2), (3-Ю)(4-Н6) 15. (5-fO)(4H-6), (3-Ь0)(2-Ь4) 11, (5-H))(4-f-2), (3-f-0)(4-(-6) Дп. (5-f-0)(4-f-6)-. (3-t-0)(2+4) A15. а+т+)< (Б-Ю)(4-Ь6> 11. (3-t-0)(2+6), (5+6) (V+6)

Они позволяют перейти от схемы (рис. 5.1) к эквивалентным ей схемам, показанным на рис. 5.2.

В рассмотренных случаях эквивалентных преобразований изменяются узлы подключения активных приборов, а конфигурация пассивной части схемы остается неизменной. Возможны эквивалентные преобразования, связанные с взаимной перестановкой определенных пассивных элементов схемы и, следовательно, с изменением конфигурации пассивной части схемы, при которых сохраняются неизмен--

/ 2

Yexi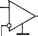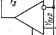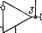

Рис. 5.2. Эквивалентные схемы, полученные из схемы рис. 5.1 на основе: а, б - преобразования (S.41); е - преобразования (5.42); г - преобразования (5.43)

НЫМИ узлы подключения активных приборов. В основе этих преобразований лежит одинаковая зависимость доминирующего полинома схемной функции от проводимости соответствующих элементов. Например, если эти проюдимости входят сомножителями только в отдельный полиномиальный член, то, очевидно,- что соответствующие пассивные элементы можно взаимно переставить местами. При этом форма самого полинома и, следовательно, сюйства схемы с идеальными активными приборами (Э->оо) сохранятся, неизменными.

Еще одним эквивалентным преобразованием пассивной части схемы может бьп-ь преобразование соединенных треугольником ре-зистйвных элементов в звезду. При этом преобразовании максимизируется суммарная проводимость резисторов, что принципиально важно при изготовлении схем методами интегральной технологии.

Целенаправленно выполняя эквивалентные преобразования узлов подключения активных приборов, можно отобрать из функционального семейства схему с благоприятным соотношением основных членов ос-

таточного полинома, например, с малым их абсолютным значением или со значением, при котором обеспечивается взаимная компенсация -влияний этих членов на свойства схемы. При этом должно выполняться определенное ограничивающее условие, накладываемое на основные члены остаточного полинома. Дальнейшую оптимизацию этой схемы можно выполнить на основе эквивалентных преобразований пассивной части путем взаимной перестановки ее элементов. При этом, например, может сниматься накладываемое на основные члены- остаточного полинома или на параметры активных приборов ограничивающее условие, обеспечивающее взаимную компенсацию остаточных членов. Наконец, преобразуя в полученной схеме соединенные треугатьником резистив-ные элементы в соединенные звездой, можно оптимизировать схему по критерию минимума суммарного сопротивления резисторов.

Исходным при решении задачи реализации является аналитическое выражение схемной функции (5.1) с численными значениями полиномиальных коэффициентов а, bj. Оно находится при решении аппрок-симационной задачи и с достаточной точностью отображает поведение схемных функций, обычно задаваемое в общем виде. В связи с ограниченными реализационными юзможностями пассивных цепей RC большинство заданных схемных функций можно реализовать только при помощи активных цепей РС. Они представляют собой сложные устройства с обратной связью, содержащие определенным образом соединенные многополюсную пассивную цепь RC и компенсирующие в .ней потери активные приборы.

Синтез пассивных цепей RC разработан достаточно полно. Поэтому естественно стремление свести путем соответствующих преобразований синтез сложных активных цепей с обратной связью к синтезу более простых пассивных цепей RC, развязанных активными, приборами. Вначале- необходимым преобразованиям должно быть подвергнуто исходное аналитическое выражение схемной функции (5.1), в результате которых особенности исходной функции будут, перемещены и займут в /7-плоскости желаемое или допустимое положение^в плане реализации их в данном классе цепей. Затем осуществляется реализация в этом классе цепей построенной преобразованной функции и выполняется топологический переход от этих реализаций к искомым схемам.

Следовательно, в основе метода синтеза лежит пара преобразований, состоящая из соответствующих друг другу преобразований функции и схемы. Первое из них является математическим и относится к части синтеза, связанного с преобразованием схемной функции. Оно позволяет от заданной функции /( (р) перейти к некоторой дробно-рациональной преобразованной функции (/?) с вещественными коэффициентами, у которой нули и полюсы расположены в определенном участке р-плоскости, в связи с чем ее реализация оказывается простой. В частности, можно построить преобразованную функцию с кратными или различными полюсами, расположенными на действительной полуоси, и нулями, расположенными тамже или в любой части уО-плоскости, за исключением положительной действительной полуоси. Функцию /Спр {р) с такими особенностями имеют пассивные цепи RC, развязанные активным прибором.

.. Исходная аналитическая схемная функция /((/?) может многократно подвергаться преобразованиям. Необходимо только, чтобы после каждого этапа преобразований полученную функцию можно было представить в виде произведения двух функций, по крайней мере одна из которых реализуется известными методами в желаемом классе цепей. Если, например, эта функция - сомножитель удовлетворяет условиям реализации в классе пассивных цепей RC, ее можно реализовать при помощи пассивной цепи RC. Если вторая функция - сомножитель этим условиям не удовлетворяет, то она, в свою очередь, подвергается преобразованиям до получения реализуемых сомножителей. Исходная и преобразованная схемные функции имеют различные особенности, поэтому данный вид преобразований является неэквивалентным. Второе преобразовдние является топологическим и позволяет от реализаций преобразованной функции перейти без изменения количества схемных элементов и величин их параметров к реализациям заданной схемной функцией. Оно связано с преобразованием схемы и состоит во взаимном замещении внешних выюдов преобразованной схемы или перемещении отдельных ее ветвей в соответствующие узлы. Пара преобразований должна быть взаимно однозначной. Каждому виду преобразования функции должна строго соответствовать определенная форма преобразования схемы.

Преобразование, связывающее заданную К(р1 и преобразованную Knpip) функции, должно базироваться на основном свойстве функции линейных электрических цепей - билинейной зависимости их от параметра схемы, т. е. линейной зависимости от этого параметра как полинома числителя, так и полинома знаменателя схемной функции. Преобразовав линейно числитель П/Др) и знаменатель d(p) заданной функции, можно.получить соответствующую ей преобразованную функцию

пр (р) == ft p (p)/dnp (р) = [ttk (р) + Хп (р)]1Ып (р) + Ха (р)]. (5. 46)

Если на преобразующий полином Xn,dip) наложить определенные ограничения, то нули и полюсы преобразованной функции Кпр(р) расположатся в соответствующих участках р-плоскости и, следовательно, их реализация может бьп-ь более простой, чем исходной функции. Многообразие возможных видов полинома х„,а(р) и значений его полиномиальных коэффициентов определяет многообразие решений задачи синтеза. При этом основное ограничение, накладываемое на полином л: ,й(р), связано с физической реализуемостью преобразованной схемной функции и возможностью топологического перехода от ее реализации к реализациям заданной функции.

3. преобразования функций и схем устройств

Простое преобразование схемной функции, при котором изменяется только ее знаменатель, назовем d-преобразованием. Его аналитическая форма следует из выражения (5.46) при л: (р) = О и имеет вид

- К (р) = Uk {p)ldk ip) Kd ip) = ftnp (p)/dnp ip) ==

= n,ip)l[dkip) + Xdip)]. (5-47)

Необходимым условием, накладываемым на преобразующий полином Xaip), является обеспечение принадлежности знаменателя преобразованной функции dnp(p) = й^{р) + х^(р) к классу полиномов Гурвица, что позволяет разложить полином на простые сомножители не выше второго порядка с вещественными положительными коэффи- -циентами. Более жесткое ограничение на полином х^р) вытекает из требования расположения корней всех или части этих сомножителей в желаемом участке р плоскости.

Многообразие возможных видов полинома ха (р) и значений его коэффициентов определяет многообразие решений задачи синтеза. Полиномы dkip) и х^{р) имеют численные значения коэффициентов, поэтому после приведения подобных членов полинома dnpip) в нем исчезнет информация о преобразующем полиноме Xd (р)- Эта информация необходима для выделения в преобразованной схеме ветви, связанной с полиномом х^{р), и топологического перехода к схеме с заданной схемной функцией К{р). Чтобы сохранить информацию, введем полином xip) в числитель преобразованной функции Knip), выделив'его знаком Л-

К (р) Кир(р) = т, (р) + X, {p)\/[d, ip) + X, ip)l (5.48)

Знак А означает, что нельзя объединять выделенный полином с полиномом rifiip) или сокращать общие множители числителя и знаменателя функции Кпр(р). Реализующая функцию (5.48) цепь должна иметь две независимые ветви, одна из которых характеризуется передаточной функцией п^(р)/Ы^(.р) + aip)], а другая -

хЛр)1ЫЛр) + хЛр)]-

Построение преобразующего полинома в случае, когда необходимо переместить только нули исходной функции К{р) выполняется аналогично, причем выделенный полином х„(р) будет находиться в знаменателе преобразованной функции:

К{р) KM = {nk{p)+Xn{p)mdk{p) + Xn{p)\- (5.49)

Объединяя простые dr и пгпреобразования (5.48) и (5.49), можно-построить сложное, при котором перемещаются как нули, так и полюсы исходной функции /С(р)-

К (/) - Кпр (р) + + Ъ (5.50)

Преобразованные функции (5.48)-(5.50) должны допускать представление в форме произведения двух и более функций

К.Р (р) = Кпр, iP) К.Р. ip) = j. . (5.51)

особенности, по К1эайней мере, одной из которых лежат в желаемом участке р-плоскости. Это позволяет в соответствующих им схемах выделить простой в плане реализации каскад на активном приборе или пассивную цепь, развязанную от остальной схемы активным

прибором, в случае преобразования (5.48) заданной функции Kip) соответствующая ей преобразованная функция имеет вид

К{р)--Кг:Ар)--щ;)- d-(). (5-52)

где ftnp г (Р) П„р 2 (Р) = tlk (р) и Ппр 1 (р) Ппр 2 (р) = Ь (р).

Аналогичйо, при преобразовании (5.49) заданной функции К{р) соответствующая ей преобразованная функция имеет вид

пр 1 (Р) flnp 2 Н + %р 2 (Р)

где dnp 1 (р) dup 2 ip) = (/?) и dnp I (p) dnp 2- ip) = .n (p), a при njdi-преобразовании. (5.50) ее

%lW . np 2 W + dnp 2 (P)

ГДе-Ппр 1 (p) Ппр 2 ip) = nft (p), Ппр I (p) Ппр 2 (P) =Xa ip), dnp I (P) dnp 2(P) =

= dk ip), dnp 1 (p) dnp 2 ip) = л: (p).

при всех формах преобразований (5.48)-(5.50) разность между знаменателем и числителем преобразованной функции d pip) - Ппр(р) = = d/lp) - п^(р) не изменяется, оставаясь такой же, как и у заданной функции. Можно построить компактное преобразование, если принять преобразующий полином линейной формой числителя или знаменателя функции К iP), например, xip) = -rikip) или л: (р) = = -dfXp). В этом случае информация о преобразующем поли1Юме непосредственно представлена в числителе или знаменателе преобразованной функции и необходимость введения выделенного полинома Xd(p) или xjp) отпадает. Такое ограничение преобразующего полинома уменьшает количество реализаций и ограничивает возможности преобразования по сравнению с общим случаем произвольного выбора Xdip) .или Xnip), но обеспечивает необходимый минимум свободы при формировании преобразованной функции и дает определенные преимущества практического характера, в частности, упрощает синтез.

Изменяющее только знаменатель функции простое или d2-npeo6-разование, при котором преобразующий полином xip) связан с полиномом nji,(p) числителя заданной функции /С(р). имеет вид

В d2-npeo6pa30BaHHH (5.55) в отличие от di-преобразования (5.48) удается установить непосредственную зависимость между заданной Kip) и преобразованной Kwip) функциями схемы. Выражение (5.55) можно записать в виде

1/К(р)+1/Кпр(р)== 1. (5.56)

Функции комплексного переменного р, сумма которых равна единице, хорошо известны в теории линейных электрических цепей и на-

зываются дополняющими. При этом можно различать прямые дополняющие функции - в данном случае 1/К(р) и 1/Кпр{р) и обратные дополняющие функции - ]<(р) и Кпр(р).

Изменяющее только числитель функции простое или Па-преобразо-вание, при котором преобразующий полином л: (р)связан с полиномом -знаменателя заданной функции К(р), имеет вид

К{р) K p(p)=[nk(p)~dkip)]ldk{p) = i-K(p). (5.57)

Из выражения (5.57) следует, что Пг-преобразованная Knpip) и заданная Kip) функции являются прямыми дополняющими.

В тех случаях, когда необходимо преобразовать числитель и знаменатель функции цепи, можно воспользоваться простыми преобразо- ваниями (5.55) и (5.57), применяя их последовательно или объединяя в одно несколько простых различных преобразований. Можно, например, построить комбинированное преобразование, при котором изменяется как числитель, так и знаменатель заданной функции Kip)-Это преобразование имеет вид

А CP) Д пр ip) - - - - -J [ 1 -

Kk(p)-K(p)

К ip) = [Kkip)-Kr,p (р)]/[1 -Кпр ip)]. . (5.59)

Это выражение можно считать как представление заданной функции kip) через йа-преобразованную функцию Knpip) и отличающуюся от Knpip) только числителем функцию Kkip)-

Полученные после одного или нескольких последовательно выполненных этапов преобразований (5.48)- (5.50), (5.55), (5.58) и (5.59) преобразованные функции Knpip) имеют нули и полюсы, расположенные в определенном желаемом участке р-плоскости. В связи с этим функции Knpip) реализуются в известном классе цепей, которые и составляют семейство преобразованных схем. Для перехода к схемам, соответствующим заданной функции Kip), необходимо подвергнуть преобразованные схемы определенным топологическим преобразованиям, выполняемым путем изменения их конфигурации. Чтобы определить эти топологические преобразования, нужно найти две цепи общего вида, например, в форме четырехполюсника, функции которых связаны соотношениями i,2-, 1,2-1 hidi-n л^г-преобразований, и установить условия взаимного перехода одной цепи в другую. Так как структура цепи полностью определяется ее F-матрицей, то фактически необходимо установить взаимосвязь изменений матричных элементов и функций цепи.

Если /С(/7) есть передаточная функция напряжения (тока) при холостом ходе (коротком замыкании) на выходе схемы, то в записи через матричные соотношения эта функция имеет следующий вид [12]:

ip) = ip)ldu ip) = iablKa, К, ip) = ip)ld, ip) = Ktlbb- (5.60)

Xk (P) Ilk (p)

tik (P)

(5.58)

Из формул (5.60) следует, что при определении функций перелачу из определителя матрицы проводимости исключаются соответствующие столбцы и строки с номерами а и fc, расположенные по периметру матричной решетки, при этом двойное алгебраическое дополнение Д.,д,б(, остается неизменным. Алгебраическое дополнение не изменяется, если изменять элементы в строке или столбце, которые вычеркиваются из матрицы проводимости при построении данного алгебраического дополнения. Следовательно, для независимого изменения числителя и знаменателя функции передачи цепи необходимо изменять элементы, вписываемые по периметру матричной решетки.

В частности, можно изменить одинаковые элементы в строке ив столбце.При этом изменится знаменатель d(p)=AJidi (р)= Д^,) функции передачи напряжения Kuip) (тока КЛр)), а ее числитель Пи(р)= ni(p)= Д^ь сохранится неизменным только в том случае, если в строке Ь(а) матрицы проводимости вместе с изменяемыми элементами входят в качестве слагаемых элементы, величины которых значительно превышают величины изменяемых элементов. Если выходной (входной) узел схемы совмещен с выходным (входным) узлом активного прибора, то в строке fc(a) матрицы будет находиться большой по величине параметр 0;, характеризующий усилительные свойства этого активного прибора.

Имеется несколько способов Т1зменен и я матричных элементов, обеспечивающих независимое изменение числителя или знаменателя функции передачи при постоянном двойном алгебраическом дополнении Дда.и, матрицы. Один из них состоит в добавлении (удалении) в соответствующих клетках строки Ь(а) и столбца Ь{а) матричной решетки параметра Y, характеризующего некоторый элемент или, в об-.щем случае, ветвь цепи. Если, например, элемент Yk включен между некоторым внутренним узлом k и общим узлом, то в матричную решетку он будет входить только в клетку с координатами kk. Переключение выхода элемента Y/ с общего узла схемы на выходной (входной) ее узел приведет к появлению слагаемого Yk соответствующего знака в клетках строки b (а) и столбца Ь{а) с [соординатами kb{ka), bb{aa) и bk{ak). Наоборот, переключение вывода элемента с выходного (входного) узла схемы на базисный приведет к удалению проводимости Fj, из соответствующих клеток строки и столбца Ь{а). Следствием этих топологических изменений схемы будет изменение только знаменателя (числителя) функции передачи напряжения (тока): в нем будет появляться или исчезать слагаемое, связанное с F* и являющееся полиномом Xd(p). Поэтому, если -преобразованной функции передачи напряжения соответствует схема (рис. 5.3,с), содержащая два последовательно включенных звена, причем в первом из них имеется связанная со входньм1узлом выделенная дг-ветвь, то для топологического, перехода к схеме, характеризующейся заданной функцией передачи /((р), необходимо переключить выделенную д;-ветвь с входного узла на выходной. Это же Топологическое преобразование соответствует П1-преобразованию функции передачи тока.

В соответствии с выражением (5.53) пх-преобразованную функцию