микросхемы как многополюсника. При этом составляют матричную решетку цепи без интегральной микросхемы, матричные параметрь!. которой затем вписьшают в соответствующие клетки решетки.

Однако даже при использовании метода вьщеления подсхем анал1{з цепи, содержащей, например, две и более микросхемы операционного усилителя, остается сложной вычислительной задачей, которую целесообразно было бы представить в виде несколькц^х более простых. Кроме того, при анализе практических, схем обычно нет необходимости учитывать все параметры интегральной микросхемы как многополюсника; достаточно ограничиться одним или несколькими определяющими параметрами. Поэтому важно знать аналитическое .представление функции, цепи в зависимости от параметра какого-либо ее элемента и матричных соотношений, характеризующих остальную часть цепи Г4, П].

Известно [3], что функцию линейной электрической цепи, например ее передаточную функцию, можно представить в виде дробно-рациональной функции с вещественными коэффициентами

где tikip) - полином числителя, корни которого могут располагаться в любой части р-плоскости, быть действительными либо состоять в комплексно сопряженных парах; dip) - полином знаменателя, или полином Гурвица, корни которого могут располагаться только в левой части р-плоскости, а в остальном быть по характеру такими же, как и корни полинома (р)-

Выражение (5.1) можно рассматривать как разложение функции линейной электрической цепи по комплексному переменному р. Если в числителе и знаменателе этого выражения выделить слагаемое, эквивалентное некоторой комплексной проводимости, связанной с определенным элементом или группой элементов (ветвью) цепи, или, в общем случае, выделить члены, содержащие параметр 0. любого элемента, то получим разложение полиномов числителя и знаменателя цепи по параметру данного элемента. Оно характеризует зависимость функции одного из параметров цепи, причем как числитель, так и знаменатель оказываются линейными функциями этого параметра [4]:

где п1(р), dkip) и Щ (р), (р) -полиномы числителя и знаменателя функции цепи при 0 = 0 и 0f = oo.

В полиномах nk(p, 0,) или dip, 0.) отсутствуют слагаемые одинакового вида, например 0,А-f-00,-, а также слагаемые, содержащие квадраты и более высокие степени величин параметров элементов, например 0?Д-, OfA и т. д. Если числитель и знаменатель функции (5.2) содержат одинаковые слагаемые, то эти слагаемые

должны иметь одинаковые знаки. Отмеченные особенности полиномов Пй(р, 0,) и dii{p, Ql) являются следствием основного свойства функции линейной электрической цепи, известного как свойство билинейности.

Полиномы rtfc(p) и щ {р), dl(p) и {р) являются функциями одних и тех же элементов цепи, поэтому они взаимосвязаны. Кроме того, форма полиномов зависит от мэста подключения элемента в схеме, но не зависит от величины его параметра 0,-. Эту связь совместного влияния нз свойства функции цепи величины параметра элемента и места его подключения можно представить в аналитической форме. Для этого запишем выражение (5.2) при помощи матричных соотношений. Если матрица' цепи и матрица элемента с параметром Qi представлены в одной системе параметров, то функция цепи

-=-а;-я;;;

в зависимости от вида функции К{р) ее числитель nk{p) и знаменатель dkip) отождествляют с определителем или соответствующим алгебраическим дополнением матрицы цепи, которые согласно выражению (5.3) можно записать в виде суммы этого же определителя или алгебраического дополнения при 0/ = О и произведения 0J- на суммарное алгебраическое дополнение Ае: Д = Д -f- 0/Де,.-Индексы дополнения Д(е^.) определяются узлами подключения элемента с параметро.м 0t. Если, например, он является четырехполюс-ным элементом односторонней связи, на выводах д, г которого появляется отклик при подаче воздействия на выводы I, t, то

A-A + Qi\,+rw+tb (5-4)

где суммарное алгебраическое дополнение Agr)l-\-) получается из определителя Д цепи, не содержащей элемент с параметром 0;, путем поэлементного прибавления строки q к строке г, а столбца / к столбцу t с последующим вычеркиванием строки q и столбца /.

Образованным строке и столбцу придается соответственно номер / и / и производится замена (перекодирование) индекса q яг г, г I на t, если они имеются среди остальных индексов суммарного алгебраического дополнения. Знак суммарного алгебраического дополнения определяется при помощи известного правила [12]: он совпадает со знаком соотношения (-1) + S где I - сумма вычеркнутых строк и столбцов после перекодирования индексов, - полное количество беспорядков среди вычеркнутых индексов строк и столбцов.

Выражение (5.4) имеет общий характер. Оно справедливо как для активного четырехполюсного или трехполюсного (четырехполюсного с общей стороной) элемента, так и для пассивного двухполюсного элемента. Если элемент трехполюсный, то в выражении (5.4) необходимо положить л = тогда

Если элемент двухполюсный, то в выражении (5.4) необходимо положить д = I и г = t, поэтому

Д = Д + 0.-Д(+ (,+ = Дв + QcAi,+ri. (5.5)

Для упрощения записи полученного соотношений повторяющиеся группы индексов, заключенные в круглые скобки, обычно заменяют неповторяющейся группой индексов в квадратных скобках. Определение Д[?+/-1 из Д остается таким же, как и А^д+гх+пу Суммарное алгебраическое дополнение AgrKQ+n = Дсс+г] можно рассматривать как определитель цепи, следующей из описываемой определителем Д цепи при закороченных (объединенных) в ней узлах д и г. Если один из индексов суммарного алгебраического дополнения нулевой, то это означает, что соответствующий вывод элемента с параметром Э/.связан с базисным узлом.

Разграничив входящие в состав цепи пассивные элементы и активные приборы, можно свести задачу анализа или реализации сложной цепи к анализу или реализации составляющих ее более простых цепей, последовательно выделив соответствующие пассивные части цепи. Поэтому важно записать функцию цепи в форме разложения по параметрам активных приборов различных типов [4]. Рассмотрим цепь, которая описывается матрицей проводимости и содержит пассив--ные элементы, и активные приборы, также характеризуемые матрицей проводимости. Такой активный прибор можно представить моделью в виде зависимого источника тока, управляемого напряжением. Если 5 - крутизна проводимости передачи, характеризующая усилительные свойства активного прибора, а <?, г и /, / - соответственно узлы цепи, между которыми протекает ток этого активного прибора от узла д к узлу г, и узлы цепи, между которыми приложено определяющее ток через прибор напряжение от. узла I к узлу t, то функция цепи

К(р, S) = [Д^ + 5Д„. (,+,кгн-/[Д + SAa, i.+mi+t)]. (5.6) Если активный прибор не описьюается матрицей проводимости, а схема без активного прибора характеризуется матрицей проводимости, то можно выполнить преобразование активного элемента (управляющего воздействия и зависимого источника) {12], которое позволяет представить свойства всей цепи при помощи матрицы проводимости. В частности, разложение функции цепи с одним активным прибором типа зависимый источник напряжения, управляемый напряжением, по параметру этого прибора имеет следующий вид [4]:

{Р, tl) = [Дп. [д+г] + ЦДп, [д+П + Ig+rW+t)], (5.7)

где Д[,-1 г] - суммарное алгебраическое дополнение, следующее из определителя матрицы проводимости пассивной части цепи; ц - коэффициент усиления напряжения, характеризующий усилительные свойства активного прибора данного типа.

Индексы в первых круглых скобках у суммарного алгебраического дополнения матрицы проводимости определяют узлы цепи, между которыми действует напряжение зависимого источника от узла q к узлу г (узлы подключения выходных вьюодов активного прибора).

Индексы во вторых круглых скобках - это узлы цепи, между которыми приложено в направлении от узла t к узлу I управляющее напряжение, определяющее напряжение зависимого источника. Следовательно,/ и /- узлы подключения входных выводов активного прибора. Для цепи с интегральной микросхемой операционного усилителя напряжения, имеющей симметричный (дифференциальный) вход и несимметричный выход, индексы суммарного алгебраического допол нени-я Ag+r){l-i-t) проставляются следующим образом. Индекс д соответствует узлу подключения потенциального выхода операционного усилителя напряжения, индекс л -базисному узлу. Индекс / соответствует узлу подключения инвертирующего входа операционного усилителя, индекс /- узлу подключения его неинвертирующего Твхода.

Разложение функции цепи с одним активным прибором типа зависимый источник тока, управляемый током, по параметру этого прибора имеет следующий вид:

К (р, а) = [А„, -t- аАп. (?+о(/-м1/[А<г. и+П + А^, (?-f-r)(/+ ]i (5.8)

где а - коэффициент усиления тока, характеризующий усилительные свойства активного прибора данного типа. Индексы д, г в суммарном алгебраическом дополнении матрицы проводимости соответствуют узлам цепи, между которыми протекает ток зависимого источника от узла д к узлу г, а индексы t, t - узлам цепи, между которыми протекает от узла t к узлу I входной ток, определяющий ток зависимого источника.

Разложение функции цепи с одним активным прибором типа зависимый источник напряжения, управляемый током, по параметру этого прибора имеет следующий вид:

К(р, R) = У +- . (5.9)

где R - сопротивление передачи, характеризующее усилительные свойства активного прибора. В суммарном алгебраическом дополнении матрицы проводимости индексы д, г соответствуют узлам .цепи, между которыми действует напряжение зависимого источника от узла г к узл'у д, а индексы I, t- узлам цепи, между которыми протекает от узла t к узлу / ток, определяющий напряжение зависимого источника.

Сопоставляя выражения (5.6)- (5.9), являющиеся математической записью свойства билинейности функции линейной электрической цепи с активными приборами различных типов, заключаем, что эти выражения характеризуются одной и той же формой суммарного алгебраического дополнения Agr)(l-\-t) и различными формами определителя или соответствующего алгебраического дополнения, описывающего цепь, из которой удален активный прибор. Различие их форм связано с тем, что при удалении активного прибора необходимо сохранить неизменным режим остальных элементов цепи. Для этого в зависимости от типа активного прибора следует совместить соответствующие узлы цепи, к которым подключается этот прибор.

Если цепь содержит несколько активных приборов, то, используй выражения (5.6) - (5.9) и последовательно выполняя преобразования, можно получить выражение определителя или любого алгебраического дополнения цепи в форме разложения по параметрам всех активных приборов:

AL = 6 + L, . (5.i0)

где Z.e = (П 0,) Д,е,).....,е„) (5.11)

- доминирующий полином (в том смысле, что при 6j-oo полином А~Щ;

б == 6 -f 66 - - (5.12)

-остаточный полином.

В правой части выражения (5.11) содержится произведение па-, раметров 0 всех активных приборов и п-кратного суммарного алгебраического дополнения A(ej,..., (е„), следующего из матрицы пассивной части цепи. Его индексами являются номера узлов подключения активных приборов, что в условной форме записи отображено при помощи разделенных запятыми индексов 6, в круглых скобках. При этом запись индексов многократного алгебраического дополнения упрощена: А(е,)( ..., (е ) означает то же, что и

А(выхе,квхб,), .. . , (вых е„)(вх e,j)-

В правой части выражения (5.12) имеется сумма, первое слагаемое которой

б = Д (5.13)

не зависит от параметра активного прибора и является определителем или соответствующим алгебраиче-еким дополнением матрицы пассивной части цепи. Второе слагаемое!

86 = е,Д(б.) + 0Ае.) + + е^О^До.!, (60 + (5.14)

содержит члены, в составе которых все возможные сочетания по одному, по два и больше параметров 6,-. В частности, для цепи с двумя активными приборами'

Д = Д -Ь 01Д,ео + 02Д(е.) + Ф.)- (5.15)

Если в состав цепи входят активные приборы тиг1а источник тока, управляемый напряжением, то определитель или любое алгебраическое дополнение цепи можно описать выражениями (5.10)- (5.14), в которых следует заменить параметр 0,- на параметр 5/, характеризующий усилительные свойства. активного прибора данного типа. При использовании в составе цепи операционных усилителей напряжения (активный прибор типа источник напряжения, управляемый напряжением) ее определитель или любое алгебраическое дополнение можно представить в виде

A=.L8+Li, (5.16)

где доминирующий полином а остаточный полином

б = б + б^ (5.18)

fi = Д[М.....[ : (5.19)

= fi(M.-.), IM. Ш.....[м. ] + М-гДГи,- . (Кг). [Из]. .... [м- 1 +

+----h liili2(M.,), (W. [из] . [м. 1 Н---- (5.20)

Для схемы с двумя операционными усилителями напряжения находим

+ М-г^м-а. (Кз) + И'хИ2А(м.,), (ц,)- (5-21)

Входящие в состав выражений (5.17)- (5.21) многократные алгебраические дополнения определяются по матрице проводимости пассивной части цепи. Аналогичные соотношения, устанавливающие в явном виде зависимость определителя Д или любого алгебраического дополнения матрицы проводимости от параметра 6j, можно записать и для цепей с другими типами активных приборов.

В качестве примера использования приведенных соотношений выполним анализ достаточно сложной схемы (рис. 5.1), содержащей две интегральные микросхемы операционного усилителя, и определим ее коэффициент передачи напряжения с учетом влияния коэффициента усиления pi,2 и входной проводимости Fbxi,2 операционного усилителя. Схему можно рассматривать как обобщенную некоторого класса схем, каждая из которых является ее частным случаем и следует из схемы при наложении соответствующих условий на величины ее элементов. Результаты- анализа схемы (рис. 5.1) будут использованы в дальнейшем для определения свойств избирательных усилителей низкой частоты при конечных значениях параметров активных приборов.

Пронумеровав в произвольном порядке узлы соединения элементов схемы, запишем ее коэффициент передачи напряжения [12] от входного узла J к выходному узлу 5 в виде отношения алгебраических дополнений матрицы проводимости:

Кгь - Ai/Axi. (5.22)

Используя выражение (5.21), представим алгебраические дополнения д15 и Ах1 в форме разложения по усилительному параметру yij2 операционного усилителя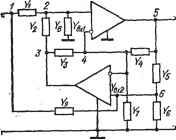

Рис. 5.1. Схема усилителя на цвух интегральных микросхемах операционного усилителя

15 = Al5, tS+0], [3+0] + И1Д1Б. (5+0)(4+2), [3+0] + + М^а^Ш, [5+0]. (3+0)(4+6) + 11215, (5+0)(4+2), (3+0)(4+6); Ац = Ди, [5+0], [3+0]+ 1111, (5+0)(4+2), [3+0] +

(5.23)

+ 211. [5+0], (3+0)(4+6) + M.iMAll, (S+0)(4+2), (3+0)(4+6). (5.24)

Для определения суммарных алгебраических дополнений, входящих в выражения (5.23) и (5.24), составим [12] матрицу проводимости пассивной части схемы (рис. 5.1), отнеся к ней и входную проводимость Увх1.2 операционного усилителя:

mn =

1 2 3 4 5 6

(5.25)

По матрице вычисляем соответствующие суммарные алгебраические дополнения. Например, для определения Ли,[5 + о], [з + о] необходимо в матрице (5.25) последовательно вычеркнуть строки и столбцы с номерами 1,5 и 3: .

Дц, [Б+О], [3+0] =

(5.26)

Для нахождения знака, проставляемого перед правой частью выражения (5.26), необходимо просуммировать индексы вычеркнутых

строк 1+5 + 3 = 9 и столбцов Г+5 + 3 = 9, следовательно. 1=9 + 9= 18. Так как индексы последовательно вычеркиваемых строк и столбцов неупорядочены, причем, общее число беспорядков равно (строка и столбец с индексом 5 вычеркивались раньше, чем строка и столбец с индексом 3), то= 2и, следовательно, определяемый соотношением (-1) + с= (-1)18+2 здар перед правой частью выражения <5.26) будет плюс. Раскрывая по известным правилам определитель, после приведения подобных членов получаем

Д„, [5+01. [3+0] = (К, + Га + Y,){Ys+ Y, + F,)(F, + Y,+ У,) +

+ Fexi {Y, + Y, + Y,){Y, + Y2 + Ys + Y,+ Y,+ Ys) + + Кех2(Г, + Y, + Y,)iY, + Y, + Y,+ Y, + Y,+ Y,) + + Fe.,F3x2(F, + Y, + Ys+y, + Y, + Y,+ Y,+ Y+Y,).

(5.27)

Аналогично вычисляем и остальные суммарные алгебраические дополнения. В частности, для определения Лц,(5 + о)(4 + 2),[з+oj необходимо в матрице (5.25) последовательно вычеркнуть строки с индексами 1, 5 и 3, затем вычеркнуть столбец с индексом I, прибавить элементы столбца 4 к соответствующим элементам столбца 2, вшеркнуть столбец 4 и, наконец, вычеркнуть столбец 3;

Д

п. (5+0)(4+2), [3+0] =

-(-1)

17+2

= (1 + У, + Ys)[УАУь + Уе + П) + Ув.2(У, + Уь)] (5.28)

Действуя аналогичным образом, из матрицы (5.25) находим

Ди, [5+0], (3+0)(4+6) =

(-1)

19+2

{Уь + Ув + Ув) [Уь{У1 + П + у в) + вх! {У, + Ув)]\ (5.29)

= YYY + YY.iY, + Y,) + Y,(YY,-YY,). (5.30)

Особенность последнего суммарного алгебраического дополнения состоит в том, что для его получения необходимо последовательно вычеркнуть в матрице (5.25) строки с индексами 1,5иЗ. Затем вычеркнуть столбец с индексом 1, соответствующие элементы столбцов 4, 2 и 6 сложить, записав результат в столбце 6, и, наконец, вычеркнуть столбцы 4 и 2. Суммирование элементов сразу трех столбцов позволяет сократить вычисления. Если же эти преобразования выполнять подробно, то сначала необходимо суммировать элементы столбцов 4 и 2, .записав результаты в столбце 2. Затем перекодировать индексы суммарного алгебраического дополнения (5.30), т. е. заменить индекс 4 в последних круглых скобках на 2 и суммировать элементы вновь образованного столбца 2 и столбца 6. Знак перед праюй частью вьфаже-нчя (5.30) определяется по приведенному выше правилу с учетом перекодирования индексов: =1 + 5Ч-3-Ь1-+-4-}-2=16. Так как вычеркиваемые индексы не упорядочены, то g = 2 и, следовательно, определяемый вьфажением (-Ip знак будет плюс.

На основе полученных соотношений (5.27) - (5.30) можно установить знаменатель коэффициента передачи напряжения схемы рис. 5.1. Используя матрицу (5.25) и выполняя аналогичные вычисления, можно установить его числитель. При этом

д15. [5-1-0], [3-f-O] = д15, [5-f-o], (3-i-o)(4-f-6) = о, (5.31)

так как по определению суммарное алгебраическое дополнение равно нулю, если оно имеет одинаковые индексы, обозначающие строки или столбцы. В данном случае в суммарных алгебраических дополнениях (5.31) дважды встречается индекс 5, относящийся к номеру столбца.

Остается определить при помощи матрицы (5.25) суммарные алгебраические дополнения

Al5. (5-l-0)(4-f-2), [3-f-O] =

= (-1)21-1-4

= Г1(Гз + Y + F,) (П + Кб + + + Пк2 [Г,(Гз +Y, + Y, + Y, + Y,)-Y,(Y, + Y,)\; (5.32)

Д15, (5+0)(4+2), (3+0)(4+6) =

( 1)20+2

г,Гз (У, + Го) + П (У^У, + У,У,-У^Ув).

(5.33)

Для получения коэффициента передачи /(15 (5.22) схемы (рис. 5.1) необходимо подставить найденные суммарные алгебраические дополнения в выражения (5.23) и (5.24), а затем построить отношение Д15/Ац. Его анализ позволяет определить передаточные свойства схемы, влияние параметров [Л и Гвх операционных усилителей, на коэффициент передачи схемы по напряжению и т. д. При малом Увх можно в первом приближении пренебречь в выражении (5.27) членом, содержащим Fbxi,2> 2 при большом р можно НС учитывать в выражениях (5.23) и (5.24) члены Aii.[5-t-o],[3+oi и Д15,[5 o],[s+o]. В последнем случае в состав числителя и знаменателя коэффициента передачи (5.22) будут входить члены как содержащие, так и не содержащие сомножитель Fp.xi,2/p.i,2, характеризующий качество оцерационного усилителя. При малом значении отношения Ув%/l можно пренебречь влиянием входной проводимости операционного усилителя на передаточные свойства схемы (рис. 5.1) по напряжению. При оо коэффициент передачи определяется отношением доминирующих полиномов

1 Б+п)(4+2). (3+0)(4+6) 11, (5+0)(4+2), (3+0)(4+6) УгУ, (Y, + П) + У^ (У^У^ + yY, - YY) - Y.YY, + Y,Y (Y, + Y,) + Y, (YY, - Y,Y,)

(5.34)

Из формулы (5.34) следует, что включение проюдимости Г, между общим приюдом и инвертирующим входом нижнего операционного усилителя изменяет в схеме характер обратной связи. При этом в знаменателе коэффициента передачи (5.34) появляется отрицательный член и, следовательно, при определенных условиях схема может терять устойчнюсть.

Некоторые свойства схемы (рис. 5.1) характеризуют .ее как схему мостового типа. В частности, при условии баланса плеч моста, образованного проводимостями У 2, Уз, У7 и Fg,

ysys = yy, (5.35)

в схеме нейтрализуется дейсчвие проводимости У, и ее коэффициент передачи при Уд= О не будет зависеть от величины проводимости У, и Fg. Это полезное качество схемы можно использовать для нейтрализации паразитного влияния емкости монтажа, воздействующей, например, как'на неинвертирующий вход верхнего операционного усилителя, так и на инвертирующий вход нижнего. Если,кроме того,