Следовательно, преобразованная схема будет представлять собой каскадное соединение пассивной схемы RC с функцией передачи (7.21/, повторителя сигналов и схемы с функцией передачи (7.22). Так как функцию (7.22) нельзя реализовать в классе развязанных пассивных цепей RC, то ее необходимо предварительно преобразовать. Для этого воспользуемся г-преобразованием (5.55), при котором можно переместить полюс с положительной на отрицательную действительную полуось р- плоскости:

К, (р) -K,d {р) = о/Ф{р -Ь, + бо) (7.23)

Аналогично выражению (7.10) функцию Кгйг (р) можно представить в виде произведения

КыЛр) - К 2{р)КАр) (7.24)

где KUp)=af/{bfp+bT) (7.25)

- функция передачи, соответствующая пассивной цепи RC первого порядка (Оо = bfy,

KAp) = h (7.26)

- функция передачи, соответствующая неинвертирующему масштабному усилителю (см. рис. 6.2,а).

Для нахождения цепи с заданной функцией передачи (7.8) необходимо сначала построить преобразованную схему (рис. 7.2, а) с функцией передачи (7.24), соединив каскадно интегрирующую цепь RC с функцией передачи первого порядка (7.25) и неинвертирующий масштабный усилитель с функцией передачи (7.26). При этом

K2M = \Gj{pCi + Gi)\{\+gJg2) .

и, следовательно,

af = bf = Ci; bf Ci, Л = 1 -f {glg). (7.27)

Подвергая эту схему топологическому йг-преобразованию (см. рнс. 5.3,г), получаем схему (рис. 7.2,6) с функцией передачи (7.23), которую следует дополнить развязанной повторителем сигналов интегрирующей пассивной цепью RC с функцией передачи первого порядка Ki (р) = G.J(pC2+ Сг),. и, следовательно,

albfG,; bV = C,. (7.28)

Образованные в результате этого схемы (рис. 7.2,(?,5) будут иметь функцию передачи (7.9) и после топологического г-преобразования дадут искомые схемы (рис. 7.2,г,е). Чтобы оценить практическое значение схем этого типа, необходимо аналогично предыдущему случаю установить зависимость -собственной частоты (7.2) и добротности (7.3) от параметров b J функций передачи пассивных цепей RC и усилительного параметра ft и выполнить анализ полученных выражений. Для этого необходимо приравнять правые части выражений (7.23) и (7.24), которые следует записать при помощи соотношений (7.25) и (7.26) в явной форме, и найти зависимость параметров и &/ от af, bf и ft, Исполь-

зуя выражения (7.9), (7.10), (7.21), (7.22) и учитывая найденные параметры а, и Ь], получаем следующие зависимости:

Ье = ао [1 + {b/af){bf/haf- 1)];

Ь, = а, [bbf + bf ibf - hdl)\!{hafaf);

(7.29)

0=1=

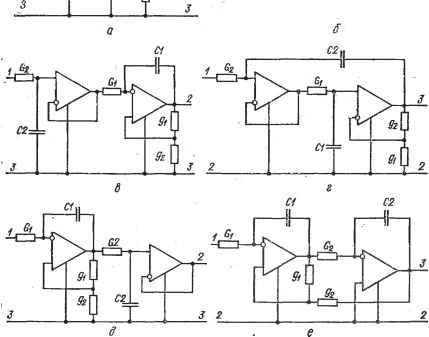Рис. 7.2. Преобразованные и конечные схемы звена нижних частот с функцией передачи (7.31)

которые после подстановки в формулы (7.2) и (7.3) приводят для случая канонической пассивной цепи(Со= fcg, af = Обследующим зависимостям:

cOn = I/CЬo/(ЬГfcf);

Qn = Vbl%fbfbfl[bfbT + bfbf (1 - Л)].

(7.30)

Из выражения для Qn следует, что при Л > О добротность звена будет выше добротности исходной пассивной цепи. Соотношения (7.27)- (7.30) позволяют записать функцию передачи схем (рис. 7.2,г,е) в виде

а собственную частоту Юп и добротность Qn й формах

io = VG-,GJiC,C,)=l/VTiT,; (7.32)

CiG-C,G,(gjg,) T,-T.Ag,/g2) l-4lgi/g.)

где 71= Ci/Gi и 72= CzlG-i- постоянные времени пассивных цепей RC; kx = 72/7i= G1C2/C1C.2- коэффициент, характеризующий отношение величин элементов пассивных цепей RC.

Чувствительность собственной частоты и добротности звена данного типа к изменению величин схемных элементов определяется следующими соотношениями:

Ьт. =Ьтз=-= 0;

Sr = Qn/i]/72/7i = Qn/iKx;

sfi = -i - Q (1 - Л) У fjT-, = 4 - Qn (1 - /I) ]/; S?: = I - Qn Т/Тут; = I - Qn lF,.

(7.34)

Формулы (7.32)-(7.34) полностью определяют свойства звеньев данного типа, которые в сильной степени зависят от коэффициента kx-Свободу выбора значения kx можно использовать для оптимизации свойств звена, в частности, минимизации суммарной емкости конденсаторов, минимизации чувствительности, получения желаемого соотношения величин элементов пассивной цепи RC, максимизации значения добротности звена Qn при данном коэффициенте h, минимизации требуемого коэффициента h при заданной добротности и др.

При благоприятном соотношении величин элементов пассивной цепи {k та \) в звене можно обеспечить независимую регулировку добротности Qn изменением усиления h=\ + gi/g2 и собственной частоты (Оп изменением величин элементов пассивной цепи. Однако чувствительность добротности оказывается высокой, пропорциональной Qn. Для уменьшения чувствительности следует уменьшать параметр h. Минимальная чувствительность добротности Qn достигается при Л = i. Соответствующие h = 1 схемы звена показаны на рис. 7.3,а,б. Они получаются из схем (рис. 7.2, г,е) при gi=0 или оо и характеризуются добротностью

Qn = УСЩС) = yTJTi = У^- (7-35)

Из этого выражения следует, что в схемах рис. 7.3 с низкой чувствительностью добротности к изменению величин элементов отношение

гg/Ti постоянных времени, цепей RC возрастает пропорционально квадрату требуемой добротности. Схемы характеризуются неблагоприятным соотношением величин пассивных элементов уже при доб-ротностях Qn. равных нескольким единицам. Кроме того, регулировки собственной частоты и добротности Q оказываются взаимосвязанными. Отмеченные недостатки ограничивают применение звеньев нижних частот этого типа.

Для получения других вариантов схем следует применить эквивалентные преобразования к схемам, пока.занным на рис. 7.2,г,е и 7.3,а,б. Кроме того, если в схеме рис. 7.3,а исключить повторитель сигналов, то получим известную схему звена нижних частот на одном операционном усилителе, работающем в режиме повторителя сигналов.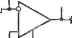

Cl2.

>

Рис. 7.3. Схемы звена нижних частот с функцией передачи (7.31) при gi =

= 0(g,= oo)

Если в преобразованной функции (7.9) выбрать коэффициент Оо- =Ьо. то один из ее полюсов расположится в начале системы координат, а другой - на отрицательной действительной полуоси. При этом функцию (7.2) можно представить в виде

(7.36)

где а„ = Ь„ = c Go йo; h = Ы'ЬГХ; h = bXX < = о-

Первый из сомножителей выражения (7.36) соответствует передаточной функции интегрирующего звена (см. рис. 6.4, а). Коэффициенты функции можно связать с величинами эле;ментов пассивной цепи звена: а .= ЬГ= Cj.

Второй из сомножителей также описывает передаточные свой-ства интегрирующего звена, в котором имеются потери, определяемые коэффициентом Ь^. Эти потери учитываются на схеме интегрирующего звена при помощи проводимости резистора, подключаемого параллельно конденсатору (см. рис. 6.13, б). Поэтому коэффициенты второго сомножителя функции (7.36) можно связать с величинами элементов пассивной цепи интегрирующего звена: = Gg, bf-C и ЬТ == Gg. Третий из сомножителей функции (7.36) соответствует функции передачи инвертирующего масштабного усилителя (рие. 6.1, 6) при flj = gv а'о = а-

Подставляя значения коэффициентов а^, fc,- в формулы (7.2) и (7.3), определяем собственную частоту и добротность Q полюсов звена данного типа:

Из анализа этих выражений следует, что звенья имеют низкую чувствительность собственной частоты сОп и добротности Qn к изменению величин пассивных элементов, которая не зависит от Q, и по абсолютному значению не превышает единицы при благоприятных соотношениях величин элементов (од = af и bf = bf, т. е. Gi = Gg, = Cg). Звенья имеют нулевую чуЕСтвительность Юп и Q к изменению усилительного параметра активного прибора при р,->оо. Ресулировки собственной частоты и добротности выполняются независимо. Добротность Qn регулируется при помощи элемента, проводимость G3 которого соответствует коэффициенту bf = Gg. Так как Gg не входит в выражение для соп, то при этом собственная частота изменяться не будет.

Из рассмотренных трех типов звеньев, соответствующих различным условиям выбора коэффициента ао при преобразовании заданной функции схемы, только последний характеризуется высокими качественными показателями при больших значениях добротности Qn. В каждом случае можно отдать предпочтение тому или иному типу звена в зависимости от конкретных требований задачи. Прн синтезе схем с высокой избирательностью основной интерес представляют звенья последнего типа. Отличительным признаком их синтеза является возможность выделения в преобразованной функции сомножителей, соответствующих функции передачи интегрирующего звена, причем в одном из таких звеньев с целью получения требуемой добротности строго дозируются потери при помощи проводимости определенного пассивного элемента, практически не влияющего на собственную частоту.

Низкая чувствительность звеньев этого типа объясняется тем, что каждый активный прибор обеспечивает определенную компенсацию потерь в связанной с ним пассивной цепи RC первого порядка. Поэтому схема звена с функцией передачи высокого порядка на одном активном приборе будет отличаться сравнительно высокой чувствительностью. Предельно низкую чувствительность можгю обеспечить в звене, число активных приборов которого не менее порядка его функции передачи.

Именно звенья этого типа следует рекомендовать для практического использования. Они рассмотрены в следующем разделе.

Ряд схем избирательньЬс усилителей нельзя синтезировать на основе йз-преобразования. Поэтому проюдимая классификация усилителей по свойствам должна быть дополнена общим анализом схем, синтезируемых на основе di-преобразования.

н. .137

Переходя от заданной функции (7.8) к ее й^-преобразованию (5.48) К(р) -> Ка, (Р) = [ о + d (рШЬ^Р' + ЬгР + Ьо + х, (р)],

можно установить, что преобразование комплексно-сопряженной пары полюсов функции К (р) пару действительных полюсов функции Kd,{p) обеспечивается при различных формах полинома ха(р). Отличные от рассмотренных выше типов схем получаются при выборел: {р)= = Uip . В этом случае преобразованную функцию можно представить в виде произведения двух сомножителей

/ ч a-iP + Op CiP/ft + ajh ,

bp + (b, + fli) P + fco bP + -i- fli) P + feo

При h 1 первый из сомножителей можно реализовать канонической пассивной цепью RC с передаточной функцией второго порядка

К\ [р) = Са\р + а о)тР + Ь р + bS).

у которой Ьо = Со. Второй сомножитель реализуется неинвертирующий масштабным усилителем рис. 6.2, а), у которого /г = 1 -f-+ (gifgi)- Между полиномиальными коэффициентами а^, bi заданной функции Кр (7.8) и а , Ь функции К {р) должна быть следующая взаимосвязь, устанавливаемая из сопоставления К {р) и первого сомножителя Kd, (рУ- а = ajh, о = Ьо = ajh = Ьд, Ь^-Ь^ и bi = = fe - a = b\ - dlh. Подставляя эти зависимости в выражения (7.2) и (7.3), определяем собственную частоту и добротность пары полюсов звена нижних частот данного типа:

При /г > О добротность пары полюсов активной цепи Qn выше добротности исходной пассивной цепии при h -> Ь^/щ может быть получена сколь угодно большой при сравнительно малом усилении. Регулировка величин Шп и Qn независима, если вначале добиваться требуемого значения изменением величин пассивных элементов, а затем требуемого Qn путем изменения усиления h. Чувствительность соп к изменению величин пассивных элементов небольшая и по абсолютной величине равна i/2. Однако чувствительность добротности Qn при h, близком Ь^/а , т. е. при высокой Qn, к изменению h и величин пассивных элементов оказывается очень большой. Поэтому данный тип схем можно рекомендовать для реализации небольших значений добротности порядка нескольких единиц, когда h получается равным или незначительно большим 1. Благодаря малому h такие схемы имеют широкую полосу рабочих частот.

Соответствующая функции. Kdi(p) преобразованная схема показана на рис. 7.4,а. Ее передаточная функция

К. (п^ - - pCiG + G,G. 4- rr /гг

da, (/>) ~ Р'СхС, + Р [СА -Ь С, (G, -Ь G,)J -Ь CG, /eU-

Подвергая эту схему топологическому di-преобразованию (рис. 5.3, а), состоящему в переносе связанной с элементом С1 выделенной ветви со входного узла на выходной, получаем схему звена нижних частот на одном операционном усилителе (рис. 7.4,6). Ее передаточная функция

Ч (Р) --Ха ip)

OlG2(l+gl/g.2)

X, (р) р'С,С, + р [С, (Gi + G,) - Ш81) CiG,] + G1G2

Наивыгоднейший случай в смысле минимизации чувствительности и обеспечения максимума полосы рабочих частот имеет место при ра-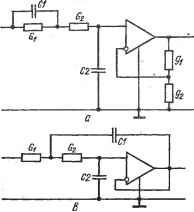

б

Рис. 7.4. Преобразованная {а) и конечные {б, в) схемы звена нижних частот на одном активном приборе

боте усилителя в режиме повторителя напряжения (рйс. 7.4, в). Тогда = 1(ё^2== 0) и функция передачи схемы

К {р) = GfillpCfi -f рС (G, + G,) + G-iGj,

собственная частота ее пары полюсов Юп == yGGjC-fi, добротность Q.Ti=VGGfiJCI{Gx-\-G. При одинаковых величинах элементов Qn = 0,5, а для получения больших Q приходится брать их величины существенно различными.

2. звенья нижних. верхних частот и полосовые

- Звено нижних частот с функцией передачи (7.8) можно синтезировать, например, на основе йа-иреобразования, переходя к преобразованной функции (7.36). Однако для этой цели можно использовать У1щй2-преобразование (5.58), которое позволяет получить и другие типы звеньев, в том числе режекторные и фазовые. При синтезе звена на основе П22-преобразования необходимо записать его функцию передачи (7.8) в форме разложения, в котором преобразованные функции Kk и Кп содержали бы сомножители, аналогичные представленным

Ш

в правой части выражения (7.36). Разделив числитель и знаменатель функции (7.8) на ЬгР^Ч- iP. получим

К iP) = Цйо ЯМ* + ЬгР)] + Mb2P + biP)]}/U + MbP + ЬгР)]\ = = {[йо /(&-2 Р -Ь Ь ) Ь[р\ + [&о/(Ь2 Р + &Г) bi>]}/( 1 + {bj{b2 р +

-fbDb.plf. . - (7.37)

где й5 + &о = а-о, bib; = b, b{bi = b-.

Сопоставляя выражения (5.59) и (7.37), находим

Kn-j.ip) --= -ьЖрЛ- Ь'О ЫР = [-&0/Ф'р + Ь'[)] X

x{-b;ib(p)(-gJg2): (7.38)

К, (р) = йо т^р + Ы') &i Р1 = l-bj цьр + bi)l i-bolbip), (7.39)

причем Ьд = (gbl)jg, gi = g2- Кроме того, при разложении функции (7.39) на сомножители принято а' Ь^Ь^. Это допустимо, так как а' является слагаемым выбираемого при синтезе коэффициента о, с точностью до которого и определяется заданная функция (7.8).

Преобразованная схема с функцией передачи (7.38) показана на рис. 7.5, а. Так как Ьд = Gj, b=:Ci, bl=Gg, bfG яЬ{=С^, то коэффициенты функции (7,8)

Ьо = С^2ёгЫ2> bCGs, Ь2 = СгС2. a,{l+gJg2)GG.{7A0)

Функция передачи сигнала из входного узла в узел k равна Kii (7.39). Выполняя п^йгпреобразование (см. рис. 5.3, д) схемы рис. 7.5, а, получаем схему звена- нижних частот, показанную на рис. 7.5, б. Ее функция передачи, определяемая на основании выражений (7.8) и (7.40), имеет вид

K(p)l{gx + g2)GiG2]l[pC,C2g2 + pC2Gsg + GAgxb (7:41) Собственная частота и добротность ее полюсов

сОп = VG.GgJjCCy, . (7.42)

Qn=il/Gs)VGxG2CxgtKC2gzy (7-43)

при

Gi = G2==G; Ci = Ca = C; g = gg (7.44)

определяются соотношениями

con = G/C; Qn-G/Gg, (7.45)

a передача звена на плоской части амплитудно-частотной характеристики /С1р=о =2.

Если коэффициент усиления операционных усилителей р^.-гххэ, то]в схеме рис. 7.5,6 можно исключить повторитель сигналов и получить схему звена нижних частот на двух операционных усилителях-(рис. 7. 5, в), также имеющего функцию передачи (7.41). При конечном Ру коэффициент передачи схемы рис. 7,5, в отличается от коэффициента передачи (7.41) малыми остаточными членами. Для их оценки необходимо выполнить анализ схемы рис. 7.5,в при конечном р., вычислив

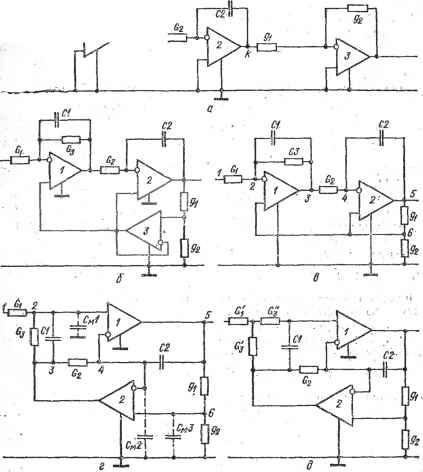si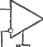

CZb4

Рис. 7.5. Преобразованная {a) и конечные (б, е, е) схемы звена нижних частот с большой добротностью н низкой чувствительностью =5=Д? параметров к изменению, величин элементов

(см. гл. 5) полиномиальные коэффициенты bf функции передачи схемы и определив по ним влияние параметра р, активного прибора на свойства звена. Имеется и другой путь решения этой задачи. Можно непосредственно- записать полиномиальные коэффициенты bf в форме разложения по параметру р^ активного прибора и величинам соответствующих реактивных элементов пассивной цепи. В частности, в полиномиальный коэффициент &2 входит произведение CiC. Поэтому его разложение по параметру р^ активного прибора и величинам элементов Ci, С2 имеет следующий вид:

Ьг =63 + b2 + Ь^ + Ь^ = С^СаДп. (3-1-0){2-1-6), (5-1-0)(4-1-6). [2-f3J, [4-f5] 4-+ ( 12/11) [3-1-0], (5-1-0) (4-f6), 12-f3], [4-f 5] + + (CiCg/Pa) All. (3-f0)(2+6), [5-1-0]. [2-1-3], [4-f 5] + + (QC2/tlH2) All. [3H-0J, [54-0], [2+3], [4+5]. (7.46)

При, pj.-v 00 коэффициент b принимает значение CiCggg (коэффициент при выражения (7.41)). Поэтому суммарное алгебраическое дополнение безреактивной пассивной части цепи (рис. 7.5,е), входящее в состав первого слагаемого коэффициента Ь^ (7.46), равно §2- Вычисления суммарных алгебраических дополнений, входящих во второе и третье слагаемые, дают соответственно g-g и gi+ ga- Отбрасывая четвертое слагаемое ввиду его малости, получаем

Ь^ = QCaga [ 1 + (1/14) + (gi + Я2)/{[2§2)1 (7.47)

Аналогично определяем коэффициенты

f-c,o*[.+€(, + £g)+i(>+-gg)

Ьо = GiCai [ 1 - + lt . (7.49)

Проанализируем свойства схемы рис. 7.5,в при условий, что в диапазоне ее рабочих частот коэффициент усиления операционных усилителей описывается выражением

1,= [Ao1+pW> (7.50)

где = l/(or, сод^. -- граничная частота усиления, т. е. частота, на которой усиление снижается на 3 дБ.

Учитывая соотношения (7.47)-(7.49) и (7.8), можно установить, что при этом условии знаменатель функции передачи схемы рис. 7.5,в будет полиномом третьего порядка

dk (Р) = fcaV + btp + btp + bt (7.51)

в котором

bt = b>-, = + b- + b- bt = bi -f b -f b;

bS==bo + b (7.52)

(7.48)