другие варианты схем получаются, например, при изменении порядка следования звеньев преобразованной цепи и,при дополнении ее повторителем напряжения.

Интегрирующее звено с коршенсацией потерь конденсатора. В ряде случаев применения интегрирующего звена (рис. 6.4,а) возникает задача компенсации сравнительно больших собственных потерь конденсатора, обусловленных проводимостью утечки С. Передаточная функция интегрирующего звена с учетом потерь имеет вид

K(p) = -G/(pC + Gu) . (6.38)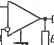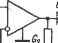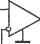

Рис. 6.J1. Пресбразованпые и конечные схемы усилительного звена с регулируемым, коэффициентом усиления h в пределах от 1 до оо (при ц. -> оо).; регулятора нижних частот; регулятора верхних частот ...

Функцию передачи схемы, в которой осуществляется компенсация проводимости Gn, можно записать в форме

K{p)=-aJ{pC + G ~bo). (6.39)

В связи с наличием отрицательного члена в знаменателе функции необходимо проводить синтез цепи на основе йа-преобразования (5.55). Построив йа-преобразованную функцию

i<- iP)Kd, (Р) = t(Co -ШрС +Gn + a,- bo)] [йо/(Со - bo)], (6-40)

устанавлршаем, что первый ее сомножитель соответствует функции передачи интегрирующего звена, содержащего конденсатор С, потери которого определяются проводимостью Gn, и резистор с проводимостью G. Поэтому

1 (Р) = {ао - ЬоЖрС -f G, + с„ - bo) = G/{pC +G + G). (6.41)

Второй сомножитель выражения (6.40) соответствует функции передачи неинвертирующего масштабного усилителя (рис. 6.2,с).

Ка-йо/(ао-Ьо)= 1 (6.42)

При каскадном соединении этих звеньев получаем преобразованную схему (рис. 6.12,й) с функцией передачи (6.40), в которой

a, = G{l +G.,/G,), b = GGjG.

(6.43)

Подвергая ее топологическому а-преобразованию (рис. 5.3,г), полу-чим схему интегрирующего звена (рис. 6.12,6), в котором обеспечивается компенсация потерь конденсатора, учитьгоаемых проводимостью Сп, включенной параллельно его емкости С. Функция передачи схемы определяется выражением (6.39), коэффициенты о и Ьо которого удовлетворяют соотношению (6.34), поэтому

К (р) = -G (1 -f GjG)l(pC + G - GGg/C,). (6.44)

\ I 1

Рис. 6.12. Преобразованная (a) к конечная (б) схемы интегрирующего звена с компенсацией потерь конденсатора

При Gn= GG2IG1 В схеме полностью компенсируются потери конденсатора, при этом ее передаточная функция

. /С (р) = - (G-Ь Gn)/pC. (6.45)

Вместо элементов с проводимостью G и рС -f Gn в общем случае в схеме (рис. 6.12,6) можно использовать двухполюсники сложного вида Yx и Fa- Передаточная функция такой схемы при р, оо .

К{р)==-\Y, (1 + Ga./Gi)]./(ra - F,Ga/Gi)

(6.46)

дает основания назвать ее компенсаторы потерь. Компенсация потерь осуществляется по цепи Gi, Ga и определяется отношением проводимостей Gg/Gi. Если, например, /1= pCgi/(pCi4-gi) представляет собой последовательно соединенные резистор проводимостью gi и конденсатор емкостью Ci, а рСг -\- - параллельно соединенные резистор проводимостью g2 и конденсатор емкостью Са, то функция передачи такой схемы

Р' Р^С,С, + р [Cg, + C,(g,-G,/G,)]+g,g, -

Эта функция с точностью до знака совпадает с функцией передачи одиночного колебательного контура LC с собственной частотой

(6.48)

и добротностью

Q = (VCiC,g,g,)/lC, + С, (g, - G.gi/Gi)], (6.49)

которая изменяется в широких пределах при изменении отношения G2/G1, характеризующего степень компенсации потерь в цепи.

При'использовании двухполюсников и Fа более сложного ъида можно реализовать цепь с функцией передачи высокого порядка и, выбирая определенным уровень компенсации потерь, добиться требуемых параметров.

Для определения влияния конечных величин параметров (х и Fbx интегральной микросхемы операционного усилителя на свойства схемы (рис. 6.12,6) необходимо ее проанализировать. В результате получим ее функцию передачи

(Fl + F,) (Gi + Gi) + Y (Fl + F, + G, + G,)

Y,Gi-YiG,

(6.50)

no которой определяем влияние ц и Fbx на Kip)-

Инерционное инвертирующее звено описывается функцией передачи

К (Р) = -Ко/а + ргКо) = -GAG2 + рС), (6.51)

где Ко = Gi/Cg, 1 = C/Gi, а величина Gg характеризует собственные потери звена.

Функция (6.51) не удовлетворяет условиям Фиалкова-Герста и, следовательно, соответствующая ей схема должна содержать активный прибор. Для ее синтеза используем соотношение (5.55) и определим

Й2-преобразованную функцию Kipf- KdSp) == Gi/(Gi+ Gg-f pC), которой соответствует схема (рис. 6.13,с). Она содержит пассивную цепь Cl, Gg, С и повторитель напряжения и удовлетворяет условиям соответствия аналитической й топологической форм йа-преобразования. Подвергая ее топологическому da-преобразованию (см. рис. 5.3,г), получаем схему инерционного инвертирующего звена с функцией передачи (6.51), показанную на рис. 6.13,6.

Недостатком этой схемы является то, что постоянная времени инерционного звена т и его коэффициент передачи Ко при р = О взаимосвязаны. Одна из этих величин прямо пропорциональна, а другая - обратно пропорциональна Gi, и это накладывает определенные ограничения на выбор величин элементов схемы. В частности, если необходимо обеспечить достаточно большую постоянную времени т инерционного звена, то приходится выбирать малую проводимость Gi, так как увеличение емкости С конденсатора может сопровождаться ухудшением его электрических и эксплуатационных характеристик. При этом для пол^ения большого значения 7(о= Gj/Ga приходится выбирать очень малую проводимость Ga, получение которой с высокой точностью является сложной технической задачей.

Чтобы устранить отмеченные недостатки, необходимо преобразовать сАему (рис. 6.13,6), введя в нее дополнительный пассивный элемент, например резистор, который обеспечил бы относительную свободу выбора величин элементов. Функция передачи напряжения схемы (рис. 6.13,6) не изменится, если между ее входом и выходом (узлы 1, 3) включить дополнительный резистор G, Соединенные треугольником элементы Gi- Сз можно заменить эквивалентными элементами Gi- Gg, соединенными звездой, при этом схема рис. 6.13,6 преобразуется в схему рис. 6.13,6.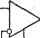

1 Ju

(лг <г

Рис. 6.13. Схемы инерционного инвертирующего звена:

о -преобразовапная; б - конечная; в, е -следующая из, схемы (рис. 6.13,6) после преобразования резистивчой цепи

Так как взаимосвязь G - G3 и G{ - Gg определяется известными соотношениями

Gi = G;G;/(Gi + Са + Оз)1

G, = Cfisl{G + G;+Gs)\ . (6.52)

Сз = G\G-j{G[ + с; + с;), j

то для определения функции передачи схемы рис. 6.13, в необходимо подставить Ci и Gg из соотношений (6.52) в формулу (5.51):

К{р) = -Gi/{C; + рС[Ц- (С, + Са)/С;]}. (6.53)

При этом оказывается, что постоянная времени инерционного инвертирующего звена (рнс. 6.13, в) т = [1 + (Cg + G)iG[] (C/Gs), а ко-эффициенг передачи при р = 0 К^ G/G. Из этих выражений следует, что можно получить большое значение Д' при большом С^ и не слишком малом С'а, тогда значительная постоянная временя

1 C/Gg будет получена прн проводимости Gg, соизмеримой по величине с G. Следовательно, при одних и тех же параметрах инерционного звена суммарное сопротивление резисторов в схеме рис. 6.13, в может быть значительно меньше, чем в схеме р*1С. 6.13, б. Другим полезньцм свойством схемы рис. 6.13, в является достаточно слабая взаимосвязь и т и возможность практически независимой- регулировки их.

Улучшение свойств схемы рис. 6.13, в обусловлено введением дополнительного резистора с проводимостью Сз.При Оз = оо эта схема преобразуется в схему рис. 6.13,6, а выражение (6.53) переходит Б (6.51). Сопоставляя выражения (6.51) и (6.53), заключаем, что введение элемента Gg эквивалентно умножению емкости С конденсатора в [[ + iGi+ Gd/Gs] раз.

В схеме рис. 6.13,6 можно включить резисторы параллельно выходу и-инвертирующему входу операционного усилителя, которые не изменяют ее передаточные свойства. Совместно с Gg они образуют рези-стквный треугольник, который можно преобразовать в эквивалентную цепь и прийти к схеме рис. 6.13,г, яналогичной по свойствам схеме р с. 6.13,в, но содержащей на один 1.С1ССИВКЫЙ элемент больше. Коэффициент передачи этой схемы описывается выражением (6.51), в KOTOpoMG2=G2G27(G2-f G-f Gg)-эквивалентная проводимость резистивной цепи обратной связи.

Преобразователь отрицательного иммитанса описывается входной функцией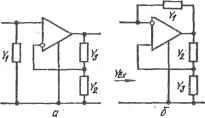

Рис. 6.14. Преобразованная (а) и ко-. нечнаяСб) схемы преобразователя отрицательного иммитанса

(6.54)

в связи с чем может рассматриваться как преобразователь проводимости, так и преобразователь сопротивления. Причем относительно элементов Yi и Ys устройство ведет себя как конвертор отрицательной проводимости, а относительно элемента У а- как инвертор отрицательной проводимости. При синтезе устройства с входной функцией (6. 54) будем считать, что преобразованию с коэффициентом -Уд/У г подвергается проводимость У^.

Учитывая соотношения (5.65) и (5.69), определяем коэффициент усиления по напряжению усилительного блока

-Уз/Уа = 1/[1 - Kui {p)h K. (р) = 1 -Ь Fa/Уз, (6.55)

Подключая параллельно входным зажимам неинвертирующего усилителя (рис. 6.2,а) с передаточной функцией Kaiip) двухполюсник с проводимостью Fl, придем к преобразованной схеме устройства (рис. 6.14,с). Подвергая ее топологическому преобразованию (рис. 5.4,а), состоящему во взаимной замене узла связанного с выходом усилителя, и общего узла, получим конечную схему преобразователя

отрицательного иммитанса (рис. 6.14,6) с входной функцией (6.54).

Если необходимо построить устройство, содержащее пару независи-мых преобразователей, то можно использовать два преобразователя (рис. 6.15,а), каждый из которых выполняется по схеме (рис. 6.14,а). При этом входные проводимости со стороны узлов 1 к4 будут соответственно

Гвх1 = -Y.YsJY, Гвх4 = -Y,Y,/Y,. (6.56)

Рассматривая схему (рис. 6.15,а) как единую, эти входные проводимости можно представить- в форме разложения по усилительному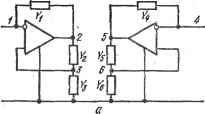

Рис. 6.15. Эквивалентные *хемы двойного преобразователя отрицательного иммитанса

параметру р оо операционного усилителя

у (2+0)(1 + 3). (5+0)(4+6) 1 вк1 - -

Y ъул =

(2Ч-Й)а+3). (5+0)<4+6)

1 1,(2+0)(-(-Э), (5+0)f4+6) 44, (2-(-0)(1--3), (S+0K4+6)

И применить к ним эквивалентные преобразования. Например, используя выражение (5.42), получаем пару из возможных эквивалентных соотношений

лг 5+0)(1+3).(2+0)/6+4)

вх - л >

- Н, (5-(-0)(1+3), {2+0)(6Ч-4)

у Д(5+0)(1Ч-3),(2-Ю){6-И) вх4 - 7*

44, {5+0)(l+.-i), <2+0)(е+4)

которой соответствует схема (рис. 6.15,6). При р, -> оо она эквивалентна схеме (рис. 6.15,а) и ее входные функции со стороны узлов 1 w 4 описываются выражением (6.54). При использовании реальных операционных усилителей с конечным значением р одна из эквивалентных схем может оказаться предпочтительнее, позволяя решить задачу оптимизации устройства по соответствующему критерию.

Глава 7

ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ НИЗКОЙ ЧАСТОТЫ \. классификац!1я уси^иителей по свойствам

Синтез сложных избирательных усилителей низкой частоты, как правило, выполняют на основе каскадного соединения простых звеньев. При этом функция сложной цепи разбивается на сомножители не выше

- второго порядка, каждый из которых'соответствует активному или пассивному звену. Каскадное, развязанное включение определенного количества таких звеньев дает искомую цепь. Каждое из звеньев можно синтезировать при помощи рассмотренного (гл. 5) метода, в основе которого лежит пара преобразований.

Передаточную функцию второго порядка можно представить: в общем виде

К (Р) = fe (Pldk (Р) = ( 2 + а,р + а^Уфр + Ь^р -Ь Ь^). (7.1)

В частных случаях отдельные коэффициенты а числителя могут отсутствовать. Функция (7.1) имеет пару полюсов и пару нулей, расположение которых на /7-плоскости определяется полиномиальными коэффициентами с и Нули и полюсы характеризуются собственной частотой и добротностью.

Собственная частота пары полюсов- это частота, на котор'ой возникают незатухающие колебания в схеме, если в ней компенсированы потери, т. е. обеспечено выполнение равенства &t= 0. Собственная час-дота (Оп определяется из соотношения Ь^р -{- &о = О при р == =/са<в=<Вп и, следовательно, описывается выражением

соп = VbJh- (7.2)

Добротность Qn пары полюсов связана с потерями в. схеме и описывается вьфажением

Qn = K&A/bi. . (7 3)

Аналогичные понятия можно ввести и для характеристики нулей функции /( (/?): собственная частота пары нулей

m ==VWt {7.4)

или ее нормированная величина . . .

г . I .

добротность пары нулей

: \ , ; (7.6)

Коэффициенты Oj-, функции (7.1) определяются параметрами схемных элементов и изменяются при изменении последних'. Влияние изменения коэффициентов Ь^. (а^) на собственную частоту полюса соп (нуля сон) и его добротность Qn (Qn) характеризуют чувствительностью

=. d In H/d \ny= (y/H) (dH/dy), (7.7)

где H - функция схемы или некоторый ее параметр, например соп, (Он или Qn. Qu, у - изменяющийся элемент схемы или связанный с этим элементом параметр, например коэффициент Ь^.

Частные варианты функции (7.1) различаются формой числителя, а форма знаменателя остается общей и является полиномом второй степени. Целесообразно рассмотреть возможные схемы, функции кото-

рых соответствуют функции (7.1) при простейшем ее числителе Пк{р) = Й01 и поставить в соответствие оптимизирующим критериям условия выбора коэффициентов при преобразованиях функции на различных этапах синтеза. Это позволит выполнить классификацию цепей по их качественным показателям, которые и определяют целесообразность использования схемы в конкретном случае.

Рассмотрим варианты выбора коэффициентов преобразования при синтезе, например, звена нижних частот с функцией передачи

К (Р) = Co/(V + biP + bo), (7.8)

где о- коэффициент, с точностью до которого при синтезе определяется функция К (р).

Если полиномиальные коэффициенты Ь,- знаменателя функции (7.8) не удовлетворяют условиям (6.2), то необходимо при помощи.выражения (5.55) построить а-преобразованную функцию

К (Р) (Р) = -аоЦЬР^ + ЬгР + Ьо-а,). (7.9)

Затем следует наложить на коэффициент такие ограничения, при которых полюсы функции (7.9) расположатся на действительной полуоси. При этом функцию Ка, (р) можно будет представить в виде сомножителей, каждый из которых непосредственно или после дополнительного применения к нему а-преобразования реализуется в классе пассивных цепей RC, развязанных активным прибором. Построив преобразованные схемы, можно после выполнения топологической формы da-преобразования перейти к искомым схемам с заданной функцией передачи (7.8). Возможно большое количество вариантов выбора коэффициента о и, следовательно, преобразованных схем с функцией передачи (7.9). В зависимости от вида коэффициента Оо конечные схемы будут иметь различные зависимости свойств от параметров активного прибора.

Имеются два случая выбора коэффициента Оо: Со< 0 = 0-При йо<6о в зависимости от значения коэффициента Oq полюсы преобразованной функции (7.9) могут располагаться либо оба на действительной отрицательной полуоси р-плоскости (pi< О, ра< 0) либо один из них будет находиться на отрицательной, а другой - на положительной действительной полуоси (pi< О, ра> 0)- При pi< О и ра<0 преобразованную функцию (7,9) можно представить в видё произведения двух функций:

Kd{p) = K4{p)f(APy (7.10)

где К (р) = а о/{Ь 2р^ + р + Ьо) (7.11)

- функция передачи двухзвенной пассивной цепи RC нижних частот;

Ыр) = -Н (7.12)

- функция передачи инвертирующего масштабного усилителя (см. рис. 6.1,6).-

в этом случае схемы звена нижних частот с функцией передачи (7.8) будут характеризоваться тем, что в их 2-преобразованных схемах разделяются пассивная избирательная и содержащая активный прибор части.

Чтобы сделать общее заключение о свойствах схем, получаемых при данном выборе коэффициента а^, когда pi< О и О, необходимо определить выражения собственной частоты (7.2) и добротности пары полюсов (7.3) звена в функции коэффициентов bf пассивной цепи RC и параметра/г. Сопоставляя выражения (7.9) и (7.10) - (7.12), находим

&о о [ 1 + bo/iha)]; b = aob?/ftaS; 1 J3

b,a,bl/{haS). j

Учитывая, что для канонической пассивной цепи RC с функцией передачи второго порядка = Ь , после подстановки выражений (7. 13) в формулы (7.2) и (7.3) определяем собственную частоту а>п и добротность пары полюсов Qn звена нижних частот данного типа:

о)п = Vb o (1 + h)/b; (7.14)

Qn = Kfoob (l+/г)/Ь?. (7 15)

Если /г > О, то добротность пары полюсов активной цепи Qn будет выше добротности исходной пассивной цепи RC: Q = Vb gbl/b1< < 0,5. Из формул (7.14) и (7.15) следуют все практические недостатки схем данного типа. В частности, получение больших значений дсброт-ности Qn связано с необходимостью обеспечения большого усиления h: добротность Qn возрастает пропорционально квадрату усиления h. Другим недостатком схёмявляется то, что с увеличением добротности Qn во столько же раз з'велпчивается и собственная частота Юп- При этом для обеспечения заданной (Оп необходимо значительно увеличивать величины элементов пассивной цепи RC, что отрицательно влияет на э-ксплуатационные характеристики звена. Кроме того, регулировки добротности Qn и собственной частоты (Оп оказываются взаимосвязаны, и это существенно затрудняет настройку. Указанные недостатки настолько значительны, что эти схемы используются сравнительно редко, несмотря на то что они имеют низкую чувствительность добротности Qn и собственной частоты ь) по параметрам как пассивных элементов, так и активного прибора, абсолютное значение которой не превышает единицы.

Преобразованные схемы (рис. 7.1, а,б)., соответствующие функции (7.10), содержат двухзвенную цепь RC к инвертирующий масштабный усилитель, при этом

. /С? (р) = Ofij[pC,C + Р (са + CG-i + Cfi) + Gfi] (7-16) и, следовательно,

fig == bl GG,; Ъ\ -f- Cfi + C2G2; bl = С.С^,

KAp)--h---gJg2- (7-17)

Преобразованные схемы (рис. 7Л,а,б) различаются порядком следования каскадов. Подвергая эти схемы d2-пpeoбpaзoвaнию (см. рис. 5.3,г), получаем конечные схемы звеньев нижних частот (рис. 7.1, е,г) с соответствующей выражению (7.8) функцией передачи

/Л ( + gi/g-2) GjG

собственной частотой полюсов

to = -/(l+g,/g2)<?iG,/(CA)

(7.18)

(7.19)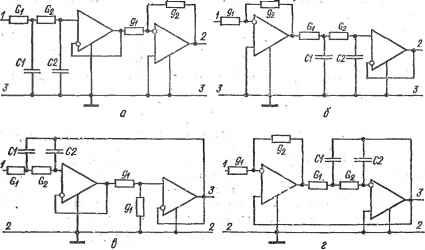

Рис. 7.1. Преобразованные н конечные схемы звена нижних частот с двухзвенной цепью RC .

и добротностью полюсов .

Qn = {У'(} + gi/g2) C.CG.GMCiGi+CG, +-C2G2). -(7.20)

Другие варианты схем звена данного типа можно получить в результате эквивалентных преобразований схем (рис'. 7.1,в,г).

Если коэффициент выбран так , что. полюсы Ьреобразованной функции (7.9) располагаются на действительной оси в разных полуплоскостях, синтез звена выполняется в следующем порядке. Преобразованную функцию (7.9) представляют в виде произведения (7.10) даух функций, одна из которых

КГг ip) = aflibfp + bf), af = b (7.21)

соответствует функции передачи пассивной цепипервого порядка, а вторая

КЛр)=--с1Жр-К), (7.22)

имеющая-полюс в правой полуплоскости,- некоторой активной цепи.