то ее можно реализовать в классе неуравновешенных -пассивных цепей RC. Если в канонической цепи с идеальным активным элементом (0. схэ) независимые от р коэффициенты ао,Ьо соответствуют проводимости G определенного резистора, то коэффициенты Oi, bi при р будут соответствовать емкости определенного конденсатора, поэтому а^р, bip - есть проводимость некоторого пассивного элемента.

Масштабным называют усилитель с заданным абсолютнымкоэффициентом передачи, точность установки которого определяется точностью соответствующих пассивных элементов. К форме амплитудно-частотной характеристики масштабных усилителей не предъявляют специальных требований, необходимо лишь, чтобы она была достаточно плоской в рабочей полосе частот. Масштабный усилитель напряжения, инвертирующий фазу входного сигнала, характеризуется передаточной функцией напряжения

K=ao/b = ~h , h >0, (6.3)

которая получается из выражения (6.1) при ai= bi = 0. Эта функция не удовлетворяет условиям (6.2), и, следовательно, она не соответствует пассивной цепи RC. Представим функцию (6.3) в форме Ц = -hjl и преобразуем ее знаменатель, например, при помощи преобразования (5.55). Полученная при эт м преобразованная функция .

K-Kd, = lhJ(h +l)]{\/l) (6.4)

соответствует функции передачи пассивной цепи RC, развязанной активным прибором.

Первый сомножитель Ki= hJ(h -{- 1) преобразованной функции удовлетворяет условиям (6.2) и его можно реализовать в классе пассивных цепей при помощи Г-образного делителя, в частРюсти, резистив-ного, с функцией передачи /(i= 12/(2+Уi), у которого Y2 - = h Yi, Y.2= С2, Yi= Gi. Второй сомножитель/(2= 1/1 соответствует функции передачи идеального активного элемента, работающего в режиме повторения входного воздействия. Схема преобразованной цепи, в которой выходной узел активного прибора совмещен с выходным узлом цепи и которая, следовательно, удовлетворяет условиям соответствия математической и топологической формам преобразования, показана на рис. 6.1,о. Подвергая ее топологическому з-преобразо-ванию (см. рис. 5.3,г), получаем соответствующую заданной функции (6.3) цепь, показанную на рис. 6.1,6.

Для определения влияния коэффициента усиления .i и входной проводимости Увх операционного усилителя на передаточные свойства инвертирующего масштабного усилителя необходимо выполнить анализ его схемы на основе разложения функции цепи по параметру активного элемента (см. гл. 5). В результате получим выражение

К = {-Y,fY,){ll 11 + -L (1 + Y,/Y, + Пк/Fj)

(6.5)

в котором первый сомножитель определяет передаточные свойства идеализированного (1.1 -> с ) масштабного инвертирующего усилителя.

Отличие второго сомножителя этого выражения от единицы характеризует вносимую за счет конечной величины р и Квх ошибку при использовании формулы

K~YJY (6.6)

для оценки передаточных свойств реального усилителя. Ошибка снижается при увеличении р, уменьшении отношения Квх/и> характеризующего качество опёрацрюнного усилителя, - и при данных у, и Увя ошибка будет тем меньше, чем меньше абсолютная величина к (6.6).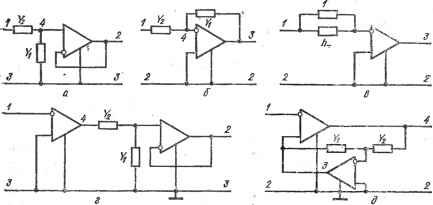

Рис. 6.1. Схемы, по.:]учаемые на раз-пирных этапах синтеза инвертирующего масштабного усилителя напряжении

ВЬфажение (6.5), характеризующее свойства инвертирующего масштабного усилителя с реальным операционным усилителем, можно получить и други.м путем, не прибегая к разложению числителя и знаменателя передаточной функции (5.7) по усилительному параметру (Л активного элемента, составлению матрицы проводимости пассивной части схемы (рис. 6.1,6) и вычислению с ее помощью соответствующих суммарных алгебраических дополнений. Для этой цели можно воспользоваться результатами, получаемыми на промежуточных этапах синтеза, и проследить, как изменяются передаточные функции преобразованных схем.

Обратимся к преобразованной схеме (рис. 6.1,а), состоящей из пассивного Г-образного звена Y-i, Y и повторителя напряжения на операционном усилителе. Синтез последнего выполняется, в частности, при помощи d2-npeo6pa30BaHHfl (5.55), причем исходным является реальный операционный усилитель, работающий в режиме инверсии сиг- нала (рис. 5.6,6) и имеющий коэффициент усиления (л и входную проводимость Fbx. Эти параметры связаны с коэффициентом передачи Кп и входной проводимостью Увх.п повторителя напряжения (рис. , 5.6,1?) преобразованиями (5.55) и (5.65), поэтому

к -(-У) М у х

1вх.п-1 -(

Учитьшая, что входная проводимость повторителя У^.п шунтирует плечо Fl Г-образного делителя в схеме (рис. 6.1,а), записываем коэффициент передачи этой преобразованной схемы

Япр - У,Кп/(Уг + Y,+ П.. п) = [хУЛУх + F) (1 + р,) + FbJ.

Конечная схема инвертирующего масштабного усилителя (рис. 6.1,6) связана топологическим йа-преобразованием с преобразованной схемой (рис. 6.1,а). Поэтому для определения его коэффициента передачи нужно воспользоваться выражением (5.55), подставив в него найденное/(пр, и найти /(. В результате придем к соотношению (6.5).

Этот пример анализа передаточных свойств синтезированной схемы с учетом реальных активных приборов свидетельствует о неразрывной взаимосвязи процедур анализа и синтеза.

Синтез этого же усилителя (рис. 6.1,6) на основе di-преобразования (5.48) проводим в следующем порядке. Представляя заданную функцию (6.3) в форме/С = -hJJ, строим при помощи выражения (5.48) преобразованную функцию

где Хй-выделенный полином. Далее необходимо выбрать значение Хй, при котором Кпр можно представить в виде произведения двух или более сомножителей, реализуемых активным прибором или пассивной цепью RC. Если, например, выбрать Xd=-1, то можно записать Кпр в форме

iCnp= [(Л + 1)/(Л +.1)](-1/0).

Сомножитель -1/0 этого выражения реализуется операционным усилителем (рис. 5.6, б) с заземленным неинвертирующим входом. Сомножитель № -f l)/(ft -- 1) можно реализовать параллельным со-* единением двух резисторов, нормированная проводимость одного из которых равна 1(F= F), а другого -ft(Fg =/iF). Поэтому преобразованную цепь можно представить схемой (рис. 6.1, е), в которой связанная с нормированной проводимостью l(Fi) ветвь является выделенной х^-ветвью. Подвергая эту схему топологическому преобразованию (рис. 5.3, а), т. е. переключая ветвь 1 со входа пре^ образованной схемы на ее выход, придем к схеме инвертирующего масштабного усилителя (рис. 6.1, 6) с проводимостями резисторов Fl и Fg = AFj.

Для синтеза инвертирующего масштабного усилителя можно использовать и другие виды преобразований, в частности, nadnpe--образование (5.58), представив

/(np-(x,-bft )[l/(l+м-

Сомножитель 1/(1 + hj) меньше 1 и его можно реализовать пассивным Г-образным делителем Fj, Fi с функцией передачи F2/(Fi-b + F2) и, следовательно, h = Fi/Fg. Возможны различные варианты выбора х^. В частности, при х^= - оо, т. е. лг =-1/0, сомножи-

гель h) реализуется инвертирующим операционным усилителем. Тогда соответствующая функции/Спр преобразованная схема примет вид, показанный на рис. 6.1,г. Для выполнения соотношения (5.63), обеспечивающего соответствие математической и топологической форм d-преобразований, эта схема допапнена по выходу активным прибором, работающим в режиме повторения напряжения входного сигнала. Для получения конечной схемы инвертирующего масштабного усилителя необходимо схему (рис. 6.1.г) подвергнуть топологическому Rdg-npe-образованию (рис. 5.3,д). Для этого в ней необходимо взаимно заместить узлы 2 и 5 и в полученной схеме снять сигнал с узла 4. В результате придем к схеме (рис.6.1,д) с функцией передачи напряжения К - -h = -Y1/Y2. Это значение обратно по абсолютной величине функции передачи напряжения схемы (рис. 6.1,6) и собсавенной цепи обратной связи, совпадающей с функцией передачи этой схемы. Следовательно, в схеме усилителя (рис. 6.1,<5) происходит обращение функции передачи цепи обратной связи.

Достоинством схемы (рис. 6.1,6) может оказаться малая входная проводимость, значительно меньшая, чем в схеме (рис. 6.1,6). При идеальном операционном усилителе с yi оо передаточная функция преобразованной схемы (рис. 6. \,а) Кир= ~У2I (Yi+ Fg), а еевход-ная проводимость Fbx. пр = 112/(1+ Fg). Так как при топологическом 2-преобразовании цепи (рис. 5.4,а) входная функция меняется по закону (5.69), то входная проводимость усилителя (рис. 6.1,6)

Пх = [Y.YAY, + П)]/11 - У,/{Уг + Fg)] = Fg. (6.7)

что указывает на наличие потенциального нуля на инвертирующем входе идеального операционного усилителя.

При этом же условии ((л оо) входная проводимость схемы (рис. 6.1,5) Fbx= 0. При конечном значении усилительного параметра л операционного усилителя Fbx так же оказывается конечной. Учитывая, что входная проводимость преобразованной схемы (рис. 6.1,г) Fbx. пр равна вхрдной проводимости операционного усилителя Fcxo. а ее передаточная функция

пр =

в соответствии с выражением (5.69) найдем входную проводимость схемы (рис. 6.1,<5)

Fbx = Fb.0/(1 - Кпр) - Fbx0/(X. (6.9)

Она не зависит от проводимостей Fi и Fg, определяющих передаточную функцию, и мала по величине.

Воз.можно большое количество схем инвертирующего масштабного усилителя напряжения. В частности, можно получить ряд схем, есш на входе преобразованной цепи (рие. 6.1) или последовательно-с Fl или Fg дополнительно включить активный прибор, работающий в режиме повторителя входного воздействия, а затем выполнить dg-преобразование полученной схемы. Заданную функцию передачи (6.3) имеют также схемы, отличающиеся от синтезированной (рис.

6.1) повторителем напряжения, включенным на ее входе или выходе. К этим схемам можно применить преобразование (5.43) и. получить ряд эквивалентных схем, которые при оо имеют функцию передачи (6.6), а при конечном (л характеризуются различными свойствами вследствие неодинакового влияния на К параметров р, и Увх активного прибора.

При Fi= Gi и Gg схема (рис. 6.1,6) имеет свойства инвертирующего масштабного усилителя. Выбирая в качестве У^ и У gразличные элементы, эту схему можно использовать в качестве функционального преобразователя, например линейного преобразователя относительного отклонения сопротивления, емкости и индуктивности р напряжение, линейного преобразователя сопротивления (проводимости) и т. д. Если вместо Y подключить нагрузку (У1=У„), то схему можно использовать как преобразователь подводимого к ее входу напряжения в ток. Действительно, точка соединения элементов У^, Уд и инвертирующего входа операционного усилителя при (л оо есть точка нулевого потенциала, поэтому протекающий через ток 1= Ух X X йвь.х. Но так как Ывь.х = -Уаг^вх/ /Уь то ii= - Угвх не зависит от

Yi, что характерно для источника тока. При этом шунтирующее действие, оказываемое схемой на источник входного напряжения, определяется проводимостью Увх. сх = f2/ bx = Уг-

Неинвертирующий фазу входного сигнала масштабный усилитель напряжения характеризуется передаточной функцией напряжения

K = aJb[=K, К>\. (6.10)

Сна не удовлетворяет условиям (6.2) и поэтому ее нельзя реализовать при помощи пассивной цепи RC. Применение к функции (6.10) преобразования (5.57)

позволяет свести ее к функции передачи инвертирующего масштабного усилителя

Рис. 6.2. Схемы, получаемые на различных этапах синтеза неинвертирующего масштабного усилителя

= 1 /г^, /г^ = 1 + й = 1 + У^/У

(6-12)

синтез которого рассмотрен выше. Поэтому, выполнив топологическое Па-преобразование схемы (рис. 6.1,6), получим схему (рис. 6.2,й!) неинвертирующего фазу входного сигнала масштабного усилителя с функцией передачи

/: = /1 = Ц-Уа/У1, Уа/У1 = Л.-1-. (6.13)

Для определения влияния конечных значений параметров (л, Увх операционного усилителя на свойства неинвертирующего масштабного усилителя (рис. 6.2,а) необходимо выполнить анализ схемы.

Пользуясь соответствующим- разложением функции цепи и вычисляя входящие в него суммарные алгебраические дополнения, получим функцию передачи схемы (рис. 6.2,а).

K = (l + Y,fY,)(l/[l+ (I/ (I + Y/Y, + YbJY,)]), (6.14)

которая при лоо переходит в функцию (6.13). Если передаточные функции (6.6) и (6.13) инвертирующего и неинвертирующего масштабных усилителей при р оо связаны п-з-преобразованием (5.57), то при конечном р между функциями передачи (6.5) и (6.14) этих усилителей нет подобного соответствия.

Соотношение (6.14) можно получить и другим путем, если воспользоваться результатами промежуточных этапов синтеза неинвертирующего усилителя. Так как схема (рис. 6.2,а) получена в результате Па-преобразования, выполненного с учетом эквивалентного для передаточной функции перемещения выходного вывода операционного усилителя с входного узла на базисный, но не являющегося эквивалентным для входной.функции, то для определения его входной проводимости следует воспользоваться разложением числителя и знаменателя функции по усилительному параметру р операционного усилителя. Записав это разложение в виде

Fbx = (A[3-f0] + pA(3-fO)(4-i-2))/(A22,[3-f-0] + рАгг, (3-f0)(4-f2))

и составив матрицу проводимости пассивной части схемы

где Fbxo - входная проводимость операционного усилителя, определим (см. гл. 5) суммарные алгебраические дополнения, входящие в Fbk. в результате получим Ар-ю] = Fbxo(Fi + Fg). А(з-н))(4+2) = О. А 22, [3-1-0] = Fl -f- Fg + FbxO и A22, (3+0x4-1-2) = Fj, поэтому

Fbx - F

Yi + Y,

Y2 + Y,o + Yi(l+li)

у 1 4- Y,/Yi

t BxO-.

(6.15)

При синтезе схемы на основе di-преобразования необходимо согласно (5.48) построить выражение Кпр = { + ха)1{1 + Xd) и выбрать Xd~ При Xd == 1 преобразованную функцию можно представить в виде

Кир = (1/ftJ (Л. - 1)/(1 - 1) = I/O + (l/ftJ(-I/0).

Первое слагаемое реализуется при помощи неинвертирующего канала операционного усилителя. Первый сомножитель второго слагаемого 1/й^ меньше единицы и реализуется пассивным делителем

Yi, У2 с функцией передачи YliYx-Y. Поэтому ЦК = YI{Y + + Y= 1/(1 + YlY-, /г+= 1 + Fa/i- причем с этим делителем связана выделенная ветвь Хц. Второй сомножитель -1/0 реализуется при помощи инвертирующего канала того же операционного усилителя. Следовательно, соответствующая преобразованной функции /Спр преобразованная схема будет иметь вид, показанный на рис. 6.2, б. Подвергая ее топологическому di-преобразованию (рис. 5.3, а), состоящему в переключении выделенной ветви со входа преобразованной схемы на ее выход, придем к схеме неинвертирующего усилителя (рис. 6.2, а).

На базе инвертирующего и неинвертирующего усилителей можно построить широко применяющиеся в различных устройствах сум-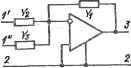

Рис. 6.3. Схемы суммирующего faj и вычитающего {б) звеньев

мирующее и вычитающее звенья. Схема суммирующего звена с двумя входами показана на рис. 6.3,а. Напряжение на выходе звена при р,- -со

вых = -[(KgWexl/ri) + (F3 exr/Ki)]. (6. 16)

Следовательно, напряжения, поступающие на входные узлы 1 и / суммируются звеном с весом Fgg/Fi. При этом наличие нулеюго потенциала на инвертирующем входе операционного усили'геля исключает взаимное влияние входных цепей на точность суммирсвания.

Схема вычитающего звена показана на рис. 6.3, б. Если ко входу Г звена приложено напряжение Нвхг, то схема работает как инвертирующий масштабный усилитель, напряжение на выходе которого г^вых' = -FgBxr/i- Если ко входу / приложено напряжение Ивх1 , то схема работает как неинвертирующий масштабный усилитель, на входе которого включен Г.образный делитель Fg, Y. Следовательно, выходное напряжение схемы при'объединенных узлах У и 2

Bb,x - [Кз/(Уз + У,] [(Fl + Y2)lYi\ Ивхг.

При воздействии на входы напряжений Ывхг и и^г напряжение на выходе схемы (р,-оо)

Ь!вых = Ивых + Ивых = -(Fg/Fi) WbxI +

+[П/(Уз+F,)][(yi-bFa)/>JtBxi . (&-17)

является взвешенней разностью входных.

2. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ

Дифференцирующие и интегрирующие звенья с отрицательной передаточной функцией. Если в качестве элемента схемы (рис. 6.1,6) выбрать конденсатор С, а Y- резистор с проводимостью G, то ее функция передачи

Kj (р) = -pC/G = -рт (6.18)

и, следовательно, схема (рис. 6.4,а) является дифференцирующим звеном. При Уз = G и Yi= рС функция передачи схемы (рис. 6.4,6)

K{p)~GlpC = ~\lp% . . (6.19)

и, следовательно, схема является интегрирующим звеном. Свойства

этих звеньев с учетом влия-С ГТ~-7-Ч ния конечных значений параметров р, Увх операционного усилителя можно установить из анализа выражения (6.5) соответственно при У^ = рС, Ух == G или Y-G, Y-ipC. Синтез дифференцирующего и интегрирующего звеньев можно выполнить при помощи преобразования (5.55) аналогично синтезу инвертирующего усилителя. Заданные функции передачи звеньев

Кл(р) =-ajp/bg, /Си (р) = -aj{bjp), а их -преобразования

Г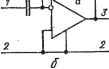

а

Рис. 6.4. Интегрирующее (а) и дифференцирующее (6) звенья с отрицательной передаточ-.;ой функцией, реализуемые на основе инвертирующего усилителя

K{p)-KdAP) =

K.(p)K.dAp}--

aiP+bo 1

Oq 1

blP + Og 1

Схема преобразованной цепи содержит каскадно включенные Г-образный пассивный делитель из элементов G и С и повторитель напряжения. Топологическое преобразование (см. рис.5.3,г) ее приюдит к конечным схемам дифференцирующего и интегрирующего звеньев, показанным на рис.6.4, а, б.

Синтез этих же звеньев можно выполнить и на основе di-преобра-зования (5.48). При этом необходимо построить -преобразованные

функции rf,

/Сд {Р) Kp.d, (р) = [- ар + лгйд ШПК + Xp.d ip)],

/Си (Р) Kd, (Р) = [ -Qo + XdM (pMbiP + Xd (р)]

и, выбрав полиномы XdB,(j}) = в виде произведения

-Ьд и Xd (р) = -Ь^р, представить их

Первым сомножителям правой части этих выражений соответствует*Пассивная ненагруженная (проходная) цепь, содержащая параллельно включенные резистор G и конденсатор С; причем в одном случае выделенная ветвь связана с элементом G, а в другом- с элементом С. Вторым сомножителям вида - 1/0 соответствует инвертирующий фазу входного сигнала идеальный активный элемент.

Включая эти цепи в той же последовательности, получим соответствующие преобразованные схемы. После их топологического rfi-преббразования (рис. 5.3 а), состоящего в переносе выделенной ветви со входного узла преобразованной схемы на выходной ее узел, получим конечные схемы дифференцирующего и интегрирующего звеньев (рис. 6.4).

При создании устройств с интегральными микросхемами часто возникает задача уменьшения величин используемых пассивных элементов. Если необходимо получить значительную постоянную времени т, например цепиС, то можно использовать сравнительно небольшие величины и С, а для обеспечения большого т использовать активную . цепь, работающую в режиме, эквивалентном умножению постоянной времени пассивной цепи RC.

Рассмотрим синтез схемы интегрирующего звена с отрицательной передаточной функцией Кк(р) = -aj{hbip), в котором обеспечивается умножение постоянной времени, пассивной цепи RC, при условии, что один из выводов ее конденсатора связан ,с общим узлом. Используя соотношение (5.48) и выбирая Ха= Ъ^, осуществляем переход к rfi-преобразоБанной функции

iHrf. (р) = (-Оо + xa)l(hbp : ха) = (-+ \)l{hbp + b,).

Так как в конечной схеме один из выводов конденсатора должен быть связан с базисным узлом, то в преобразованной функции K di ip) необходимо выделить соответствующий функции передачи пассивной интегрирующей цепи RC сомножитель вида С/{рС + G). Поэтому разложение функции Kudi ip) на сомножители необходимо выполнить в виде

Кы, {Р) = {~aJbo + 1) [{b,/h)/{bp +.bjh)].

Первый из сомножителей представляет передаточную функцию вычитающего звена (рис. 6.3,6), а второй - Г-образного пассивного делителя на элементах Gg и С. Поэтому соответствующая функции /<Hdi ip) преобразованная схема имеет вид, показанный на рис. 6.5,а. Для обеспечения возможности выполнения топологической формы di-преобразования она дополнена по выходу активным прибором, работающем в режиме повторения напряжения. Передаточная функция преобразованной схемы

K.d (р) = [ + (, + о\

поэтому для получения конечной схемы с требуемыми свойствами на величины элементов преобразованной схемы необходимо наложить сле-

дующие ограничения: bj =.С; bjh = G3; 64(1 + G2/Gi)/(G4+ Gs) = 1, откуда G2G4= g1g5, aJK = GJGi = h.

После топологического di-преобразования этой-схемы (рис. 5,3,й) придем к конечной схеме интегрирующего звена (рис. 6.5,6) с требуемыми свойствами. Ее передаточная функция

к (п\ - ntf, (P)--rf G,Gs (g4 -f g5) .

~ (P) - rf ~ pCGi (G, -f G,) -f g3 (G,G4 - GG,)

ппи условии GiGi Gfi;, соответствует передаточной функции идеального интегрирующего звена с умножением постоянной времени в h ~ = Gi/Gg раз.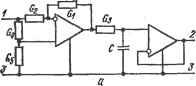

Рис. 6.5. Схема интегрирующего звена с отрицательной передаточной функцией и умножением постоянной времени пассивной цепи RC, у которой один из выводов конденсатора связан с общим узлом

Недостатком схемы является высокая чувствительность ее передаточной функции к изменению величин пассивных элементов, связанная с наличием разностного члена g2g4 - g1g5 в знаменателе.

Приближенно дифференцирующие и интегрирующие звенья с положительной передаточной функцией описываются выражением -

ip) = а^рЦа^р + а^); /Си (р) = c/( iP + с).

в котором коэффициент о связан с проводимостью G резистора, а коэффициент - с емкостью С конденсатора пассивной цепи, имеющей собственную постоянную времени То = CIG.

Соответствующие цепи с умножением постоянной времени должны иметь функции передачи

/Сд (р) = haip/iha + а^) = а^рЦа^р -Ь ajh);

/Си (р) = aj(haip + о) = ( о !) (OiP + ajh).

Подвергая эти функции 2-преобразованию (5.55), получаем пре- образованные функции

Kf,d,{p)~haipja; Kd,(p)=-aj(hatp). ,

Первая из них реализуется, например, каскадным включением дифференцирующего звена (рис. 6.4,6) с функцией передачи Kiip) = =. -pC/G и неинвертирующего усилителя (рис. 6.2,а) с функцией передачи Kz - h= 1 + Gg/Gi- Для построения схемы с другой функцией