передачи напряжения можно представить каскадным соединением звеньев, во втором из которых имеется выделенная х„-ветвь. Для перехода от преобразованной схемы к схеме с заданной функцией передачи К(р) необходимо переключить выделенную д; -ветвь с входного узла на выходной (рис. 5.3,6). Это же топологическое преобразование соответствует di-преобразованию функции передачи тока.

Объединяя рассмотренные преобразования, можно построить топологическое преобразование (рис. 5.3,в), соответствующее nidj-npe-образованию (5.54) схемной функции передачи.

п

/ -Ветвь

с с а

с с б'

в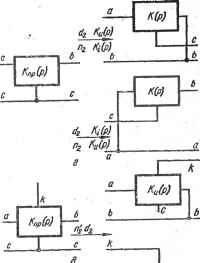

Рис. 5.3. Топологические формы преобразования схемы, соответствующие различным видам преобразования функции передачи

.при данном способе изменения элементов, расположенных по периметру решетки матрицы, часть элементов строки с(Ь) прибавляется к элементам строки b\d), а элементов столбца аф) к элементам столбца Ь(а). Добавление части элементов соответствует переключению вывода элемента или группы элементов схемы с входного (выходного) ее узла на выходной (входной). Другим возможным способом изменения элементов, расположенных по периметру матричной решетки, является прибавление всех элементов строки Ь(а) к элементам строки а(&), а^элементов столбца Ь{а) к элементам столбца аф). Такое прибавление элементов изменяет матрицу схемы. Поэтому функция передачу напряжения (тока) схемы с вновь образованной путем прибавления элементов матрицей проводимости имеет вид

Ки пр (р) = - А(а+Ь)ь/А(а--Й(а-ЬЬ) ~ - /Си (/7)/(1 - й/Сы (р));1 пр (р) -Аа(б+ )/А(а+6)(а-ЬЬ)- = -O.iKi (р)/{1 - а</С^ (р), j

(5.61)

где К„ (/?)(/С,-(р))-функция передачи напряжения (тока) схемы с исходной матрицей проводимости

,( -ff;)/(. = (-ts)/(-Is) <-2)

- При

а„= 1 {al= 1) (5.63)

функции передачи конечной и преобразованной схем будут связаны г-преобразованием (5.55). Это условие будет выполнено, если подвергаемая з-преобразованию схема характеризуется большой однонаправленной функцией передачи тока (напряжения) Ааь/АьбЭ> 1, Ац / Afca < 1, (А„ь/А„д>1, ba/bb- !) Чтобы установить топологическую взаимосвязь этих схем, следует обратиться к неопределенной матрице схемы. Матрица проводимости искомой схемы с функцией передачи /((/?) и матрица проводимости преобразованной схемы.с функцией передачи Кщ>(р) получаются из неопределенной матрицы вычеркиванием соответствующих строки и столбца с одинаковым номером, причем узел схемы с этим же номером становится общим, и перестановкой элементов в зависимости от того, какой узел схемы является входным и выходным. С учетом этого заключаем, что аналитической форме Й2-преобразования (5.55) функции передачи напряжения (тока) соответствует топологическая форма (рис. 5.3,г) преобразования схемы, состоящая в перестановке выходного (входного) и базисного ее узлов. Условием взаимноро соответствия этих форм преобразований является выполнение равенства (5.63).

Топологическая форма Пз-преобразования определяется аналогично и оказьшается дуальной (з-преобразованию. Поэтому топологическое п2-преобразование схемы с функцией передачи тока (напряже--ния) выполняется по той же форме (рис. 5.3), что и з-преобразование схемы с функцией передачи напряжения (тока), и состоит в перестановке входного (выходного) и базисного ее узлов.

Особенностью п-преобразования является то,чтодля еговыполне-ния не нужно накладывать на схему каких-либо дополнительны' условий, обеспечивающих соответствие математической и топологической форм преобразований. Действительно, топологический переход от искомой схемы к преобразованной соответствует переходу от функции (5.60) передачи напряжения (тока) к функции

Ки пр (р) = -Аа(Ь+а)/аа = 1 - аь/Ка = I - Ки (рУЛ

Ki пр (Р) = -A(,+WAbb= 1 - А.ь/Дьь = 1 - /СИР). i

Выражения (5.64) показывают, что при пз-преобразовании схем (рис. 5.3,г) зависимость (5.57) между их функциями передачи выполняется точно.

Соответствующее Пзг-преобразованию (5.58) функции передачи топологическое преобразование схемы показано на рис. 5.3,5. Слева изображена преобразованная схема, функция передачи которой от входного узла а до выходного узла b равна Кпр{р), а от узла а до внут-

реннего узла k - Kkip) - Выполнив перестановку базисного с и выходного b (входного а) узлов и сняв (введя) сигнал в узле k, получим схему, показанную справа на рис. 5.3, д. Она имеет функцию К{р) передачи напряжения (тока), связанную Пза-преобразованием (5.58) с функци- ями Knvip) и Kkip)

При da И Па-преобразованиях (5.55) и (5.57) можно непосредственно по заданной функции /((/?) найти преобразованную функцию Кпр(/>)-Затем, решая задачу синтеза, построить преобразованную схему и, применяя топологическое преобразование (рис. 5.3,г), определить искомую схему. При использовании Паа-преобразования несколько изменяется только характер решения первой части задачи, состоящей в нахождении функции передачи Kkip) и Knpip) преобразованной схемы по заданной функции передачи к{р) путем соответствующего разложения ее. Подвергаемая п'а^а-преобразованию схема, так же как и схемы, подвергаемые di- или а-преобразованию, должны удовлетворять определенному условию: их выходной (входной) узел должен быть совмещен с выходным (входным) узлом соответствую щего активного прибора.

Аналитическая и топологическая формы -преобразований взаи,!-но соответствуют друг другу, если выполняется условие (5.63). Оно обеспечивается при Абь/Аоь<1 и Аьа/Ада < 1 (А а/Д„б< 1 и и Дьа/Дьг,<С 1), т. е. при преобладании одних матричных элементов схемы над другими.

Если схема преобразована к четырехполюснику, то между ее параметрами должны бьп-ь соответствия: . Fij/F1 и Fia/FaaCl J (Ум/У2i<. 1 nFia/Fn-Cl). Следовательно, подвергаемая d-преобра-зованию схема с передаточной функцией напряжения Ки(р) должна иметь большое однонаправленное усиление по току Кшр{р)= У21/ Уц-> со,/(гобрч/?) == Fia/Faa-O, а подвергаемая d-преобразованию f схема с передаточной функцией тока Ki(p) должна иметь большое ,1, однонаправленное усиление по напряжению Кипр {р)= Fai/Faa-oo /Сиобр(р) = Fia/Fii-> 0. Первую из этих схем можно подвергнуть -преобразованию, если ее выходным каскадом является, например, транзистор в схеме включения с общим эмиттером или коллектором или если ее выходным каскадом является интегральная микросхема с соответствующими передаточными свойствами по току. Это преобразование нельзя выполнять, если схема содержит один транзистор, . причем его база соединена с общим узлом (Kj<l)- Для подготовки такой схемы к -преобразованию ее выходную часть следует дополнить каскадом, работающим в режиме повторения входного напряжения. Аналогично, вторую из указанных схем можно подвергать й-преобра-зованию, если ее выходным каскадом является, например, транзистор в схеме вкл ючения с общим эмиттером или базой, или если ее выходным . каскадом является интегральная микросхема с соответствующими передаточными свойствами по напряжению. Это преобразование нельзя выполнять, если схема содержит единственный транзистор, коллектор которого соединен собщим узлом (/( <!). Для подготовки такой схемы к d-преобразованию ее выходную часть следует дополнить каскадом, работающим в режиме повторения входного тока.

При Пз- и £/2-преобразованиях определитель канонической матрицы проводимости цепи сохраняется неизменным, а ее алгебраические дополнения изменяются по определенному закону. По этому же закону будет изменяться знаменатель входной проводимости схемы при холостом ходе на ее выходе Yx = Д/Аоа или знаменатель выходной проводимости схемы при холостом ходе на ее входе Квых = -A/Af,6, а числитель этих функций сохранится неизменным. Учитывая характер изменения алгебраических дополнений определителя матрицы проводимости, можно установить, что по закону

А(а-ЬЬ) (оН-Ь) I У be к. к/(1--Аг (/?))

изменяются при г-преобразовании входная, а при Пг-преобразовании выходная проводимости схемы в режиме холостого хода соответственно на ее выходе и входе. Кроме того, по закону

V V а+Ьна+Ь) j у с к. з (1 - (р)), аа.ЬЬ (Тбск. з(1 -К i{p))

изменяются при яз-преобразовании входная, а при з-преобразовании выходная проводимости схемы в режиме короткого замыкания соответственно на ее выходе и входе. В выражениях (5.65) и (5.66) КЛр) и /(,.(р)-функции передачи напряжения и тока схемы, у которой узел а - входной, b - выходной, с - общий.

Законы изменения входных функций приближенные. Они справедливы при выполнении условий

П. 5=. x (1 - Ки (р)) :>Yacx.x{\-Kuotp (Р)У, Уьск.э{1-Ки (Р)) к. , (1 - ки обр (Р))

или

Уасх.х{1~К^ (Р)) Y . Г1 - Ki обр {Р)У, YacK.s(l-- К, (р)) > Y-bc к. 3 (1 - Ki обр (Р))

(5.67)

(5.68)

где/Ск обр(/7) и /С обр (р) -функции передачи напряжения и тока в направлении от выходного узла b схемы к входному узлу а.

При синтезе схемы по заданной входной функции необходимо в соответствии с выражениями (5.65) и (5.66) построить преобразованную схему с требуемыми входной и передаточной функциями. В наиболее простом случае преобразованная цепь строится путем каскадно-развя-занной реализации из двух блоков. Один из них-двухполюсник с необходимой входной функцией, другой- трехполюсник с необходимой функцией передачи, обеспечивающий также выполнение условий соответствия (5.67) или (5.68) и взаимную развязку блоков.

На рис. 5.4, а показаны топологические преобразования схем, которым соответствует преобразование входных функций

Y==YJ{l-k,{p)). г (5.69)

а на рис. 5.4,6 - топологические преобразования схем, которым соответствует преобразование входных функций

(5.70)

в выражениях (5.69) и (5.70) ki(p), /Сг(р) - функции передачи напряжения или -тока трехполюсного блока от узла / к узлу 2 при общем узле 3.

£

2 Ь Y

1Г

Ь 2- £

1 ь

Рис. 5.4. Топологические формы преобразования схемы, соответствующие различным видам преобразования входной функции

В качестве примеров использования полученных результатов рассмотрим преобразования активных приборов с целью реализации иа их основе устройств с обратной связью. Исходным выберем транзистор в схеме вк.чючения о общим

0(1)-

-b[2)

-С(3)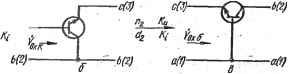

Рис. 5.5. Топологические преобразования транзистора, приводящие к трем схемам вклю.чения

эмиттером (рис. 5.5,а). Ее свойства охарактеризуем функциями передачи напряжения /С„э(р) и тока ki{p), а также входной функцией - входной проводимостью yK.s Так как схема с общим эмиттером инвертирует фазу входного сигнала,- передаточные функции ki,{p) и к({р) должны быть взяты со знаком ми-

нус. Схема характеризуется большим однонаправленным усилением, напряжения и тока. В ней выполняются условия (5.63) и (5.67) соответствия аналитической и топологической форм преобразований, и, следовательно, ее можно подвергнуть как 2-, так и йа-преобразованию.

Осуществим взаимную перестановку в преобразованной схеме выходного Ь и базисного с узлов, сохранив входным узел а (рис. 5.5,6). Учитывая топологические преобразования (рис. 5.3,г), находим, что при таком преобразовании схемы функция передачи напряжения преобразуется по закону а-преобразования (5.55), функция передачи тока - по закону Па-преобразования (5.57), а входная функция изменяется в соответствии с выражением (5.69). В результате найдем функцию схемы с общим коллектором, выраженные через функции схемы с общим эмиттером: функция передачи напряжения

1<иАР) = к^{р)1{\+к^ф)); (5.71)

функция передачи тока

к(Р) =1 + ,э(Р): (5-72)

входная функция

>в..к = лх.э/(1+4э(Р))- (5-73)

Переставим взаимно в схеме (рис. 5.5,а) входной а и базисный с узлы, сохранив узел b выходным. При таком преобразовании схемы (рис. 5.5,е) функция передачи напряжения изменится по закону Ид-преобразования (5.57), функция передачи тока - по закону а-преобразования (5.55), а входная функция изменится в соответствии с выражением (5.69). Поэтому функции полученной схемы с общей базой (рис. 5.5,е), записанные через функции схемы с общим эмиттером, будут иметь вид: функция передачи напряжения

kit (Р) = (р)/(1 + ki, (р)); (5.75)

функция передачи тока входная функция

Кх.б = Увх.в(\+к {р)). (Б.76)

Применение топологического da-преобразования к схеме с общим эмиттером, т. е. схеме без обратной связи, позволило перейти к схеме с предельно глубокой обратной связью по напряжению - схеме с общим коллектором (повторитель напряжения), а применение к ней Па-преобразования позволило перейти к схеме с предельно глубокой обратной связью по току - схеме с общей базой (повторитель тока).

В качестве другого примера рассмотрим применение преобразований к активному прибору типа операционный усилитель напряжения с симметричным дифференциальным входом и несимметричным выходом (рис. 5.6, а). При функции передачи напряжения р±-> оо, входной и выходной проводимостях Y О и Y-oo операционный усилитель считают идеальным активным прибором и описывают моделью зависимого источника напряжения, управляемого напряжением. Усилительные свойства такого идеального активного прибора можно записать в виде дробной функции р±= ±1/0.

Так как а или йапробразованию подвергается трехполюсная схема, то предварительно один из входных узлов операционного усилителя, например неинвертирующий, необходимо связать с общим. Полученная схема (рис. 5.6,6) имеет функцию передачи напряжения Ки= -1/0 и удовлетворяет условиям соответствия (5.63). Подвергая ее da-иреобразованию (см. рис. 5.3,г), получаем показанную слева на рис. 5.6, е схему с функцией передачи идеального повторителя напряжения /< = (1/0)/(1 + 1/0) = 1/1.

Особенность схемы состоит в том, что вывод активного прибора, который служит потенциальным выходом в преобразованной схеме (рис. 5.6,6), соеди-

ней с общим узлом. Это связано с тем, что при топологическом п^- или dg-npe-образовании схемы происходит перемещение ее внешних узлов, в том числе и связанных с этими узлами выводов активных приборов.

В таком активном приборе, как транзистор, любой из выводов можно соединить с внешним узлом схемы независимо от того, является ли ои базисным (общим), входным или выходным. Поэтому при выполнении условия соответствия (5.63) топологические щ-, d- и /гаа-преобразования схемы с транзисторами проводятся без каких-либо дополнительных условий- В интегральной микросхеме операционного усилителя напряжения с несимметричным выходом определенный вывод должен всегда соединяться с базисным узлом, а другой, потенциальный вывод,- с нагрузкой. Поэтому, чтобы схема, показанная слева на рис. 5.6,fi была работоспособной при использовании в ней реальных активных приборов, ее необходимо преобразовать, обеспечив связь потенциального вывода активного прибора с выходным узлом цепи. Для этого следует выполнить эквивалентное преобразование (5.42) функции передачи напряжения и по нему построить эквивалентную схему.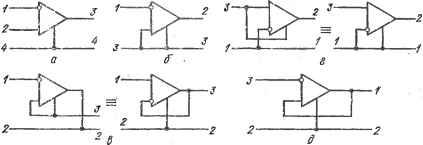

Рис. 5.6. Операционный усилите-пь и схемы, полученные в результате его топологических преобразований

Записываем числитель и знаменатсчь функции передачи напряжения Данной схемы в форме разложения (5.7) по усилительному параметру активного прибора. При .1 оо функция передачи имеет вид

. 13, (2--3)(ГЧ-3)Дп,(2-)-3)(1-1-3)- ()

В схеме с реальным операционным усилителем его общий вывод должен быть связан с общим узлом схемы. Соответственно этому в выражении (5.77) необходимо переставить индексы 2 и 3 в первых круглых скобках суммарных алгебраических дополнений. Чтобы сохранить неизменными значения числителя и знаменателя функции /( , необходимо также выполнить перестановку индексов 1 и 3 во вторых круглых скобках суммарных алгебраических дополнений. В результате приходим к тождественному соотношенрио (5.77) выражению

(5.78)

- 13. (3+2) (3+1)/!I, (3+2)(3+1)-

ПО которому строим эквивалентную схему, показанную справа на рис. 5.6,в и являющуюся повторителем напряжения.

Смысл выполненных эквивалентных преобразований состоит в том, что, если изменена фазировка выходной цепи для обеспечения соединения общего вывода операционного усилителя с общим выводом схемы, то для сохранения неизменной функции передачи необходимо также изменить фазировку его входной цепи.

В дальнейшем при синтезе иа основе преобразования (5.55) схемы с активными приборами, напритиер, интегральными микросхемами операционного усилителя с несимметричным выходом, у которых активный элемент имеет фиксированное положение относительно базисного узла, будем опускать промежуточные схемы, аналогичные приведенной слева на рис. 5.6,в, и считать, что dg-

4* . 99

преобразованием (5.55) связаны преобразованная (рис. 5.6,6) и показанная справа на рис. 5.6,fi конечная схемы. Таким образом, для выполнения топологического а-преобразования схемы с операционным усилителем напряжения, выходной вывод которого совмещен с выходным узлом схемы, необходимо соответственно переместить его выходные выводы и изменить их фазировку.

Выполненное йа-преобразование позволило, так же как и в случае с транзистором, перейти от схемы без обратной связи (рис. 5.6,6) к указанной справа на рис. 5.6,fi схеме повторителя напряжения с предельно глубокой обратной связью по напряжению

Если схему (рис. 5.6,6) подвергнуть топологическому Па-прёобразованию, то получим показанную слева на рис. 5.6,г схему с функцией передачи по напряжению Ки= 1 + 1/0. Однако эту схему нельзя использовать на практике, если входящий в ее состав операционный усилитель должен иметь, определелнкй вывод, связанный с общим узлом. После топологического п-преобразования схемы этот вывод оказался перемещенным с базисного узла на входной. Воспользовавшись эквивалентными преобразованиями, можно возвратить соответствующий БИходиой вывод интегрального операционного усилителя на базисный узел. Действительно, функция передачи напряжения показанной слева на рис. 5.6,г схемы, записанная в форме разложения суммарных алгебраических дополнений ее числителя и знаменателя по усилительному параметру р -оо активного прибора, имеет вид

Ки = Аз2 (2+3)(l--3)/33, (2+3)(1+3)- (-79)

Применим к ней эквивалентное преобразование (5.41), сводящееся к замещению индекса 3 в первых круглых скобках индексом 1 базисного узла. В результате получим тождественное соотношению (5.79) выражение

Ки = Дз2 (2+1)(1+3)/33, (2+1)(1+3)> (5.80)

по которому строим показанную справа на рис. 5.6,г эквивалентную схему с функцией передачи напряжения при идеальном операционном усилителе Ки = 1/0.

Следовательно, при топологическом Па-преобразовании схемы с операционным усилителем, общий вывод которого должен быть связан с базисным узлом схемы, достаточно выполнить перемещение только входных выводов операционного усилителя, а соответствующий выходной вывод не перемещать, оставляя его соединенным с базисным узлом. Однако такому преобразованию инвариантны только передаточные функции, а входная функция аналогичного свойства не имеет. Это объясняется тем, что при перек.чючении выходного вывода операционного усилителя с входного узла схемы на базисный уменьшается нагрузка на источник входного сигнала и, следовательно, уменьшается входная проводимость схемы. Поэтому для определения входной проводимости схемы, полученной путем 2-преобразования некоторой схемы с операционным усилителем, нельзя пользоваться выражениями (5.69) и (5.70) и приходится выполнять анализ на основе разложения числителя и знаменателя функции по усилительному параметру активного прибора р

Например, схема повторителя напряжения, показанная справа на рис. 5.6,г, получается путем da-преобразования схемы (рис. 5.6,6) с учетом эквивалентного для передаточной функции преобразования. Их входные функции связаны соотношением (5.69), поэтому входная проводимость повторителя напряжения Y = KgxQ/(l -j- р), где Kgj- входная проводимость операционного усилителя. Инвертирующий усилитель (рис. 5.6,6) и инвертирующий усилитель, пока-ванный справа на рис. 5.6,г и следующий из первого при Па-преобразовании его схемы, имеют одинаковые входные проводимости, и, следовательно, соотношения (5.69) и (5.70) в этом случае не выполняются.

Данные результаты получены при использовании пары преобразований для решения задачи анализа: исходная схема активного прибора подвергалась со-.ответствующему топологическому преобразованию и вычислялись функции полученных схем. Эти результаты, не только иллюстрируют возможности метода преобразований. Они показывают особенности преобразования активных при-

боров типа операционный з'силитель напряжения с несимметричным выходом н И будут использованы в дальнейшем.

Теперь воспользуемся парой преобразований для синтеза схемы по задан-

ной функции передачи напряжения Ки = -У(-1). Эта функция не .удовлетво-риет условиям реализации в классе пассивны.х цепей RC. Более того, отрицательный знаменатель функции передачи Ки указывает на то, что соответствующая ей схема будет неустойчивой, однако это не является препятствием для синтеза. Подвергнем, заданную функцию Кийг-преобразованию (5.55) и перейдем к преобразованной функции Ки= 1/(-1)/[1 + 1/(-1)1 = 1/0. Ей соответствует схема неинвертирующего каскада на операционном усилителе, показанная справа на рис. 5.6,г. Выполняя над ней топологическое йз-преобразование (рис. 5.3,г), придем к искомой схеме (рис. 5.6,5) с заданной функцией передачи напряжения /С„= -1(-1)-

Воспользуемся di-преобразованием (5.48) для получ-ения рассмотренных схем с функциями передачи напряжения = 1/1 и Ки - -1/(-1)- В первом случае di-преобразованная функция имеет вид /С„пр== (1 + л:)(1 + xJ. Ranee необходимо выбрать значение преобразующего полинома, чтобы преобразованную функцию можно было реализовать при помощи операционного усилителя (рис. 5.6,а). Единственное приемлемое значение х^= -1, тогда К^р - - !-1)/0. Этой функции соответствует схема (рис. 5.6,а) с объединенными входами (узлы / и 2 совмещены в один узел), причем выделенная ветвь х^ =-1 связана с инвертирующим входом операционного усилителя. Перемещая ее в соответствии с топологическим преобразованием (рис* 5.3,а) с входного узла на выходной, придем к показанной справа на рис. 5.6,г схеме повторителя напряжения с заданной функцией передачи.

Во втором случа£ di-преобразованная функция имеет вид К^р = (1 +

+Xd)/(-1 + %). Реализацию этой функции при помощи операционного усилителя (рис. 5.6,а) обеспечивает единственное приемлемое значение преобразующего полинома 1. Тогда функция К„пр=(-1 + 1)/0 и, аналогично предыдущему случаю, ей соответствует схема (рис. 5.6,а) с объединенными узлами / и 2, однако выделенная ветвь xj= \ связана с неинвертирующим входом операционного усилителя. Перемещая ее с входного узла на выходной, придем к схеме (рис. 5.6,5) с заданной функцией передачи.

Рассмотренный метод синтеза линейных активных цепей позволяет решать две основные задачи синтеза.

Первая задача связана с отысканием по заданной передаточной или входной функции функционально полного набора канонических реализаций данного типа. Синтез без ограничивающих условий не однозначен. Поэтому, если не ограничить количество используемых для построения схемы элементов, то заданной функции может соответствовать неограниченное количество реализаций. Однако при определенном количестве используемых элементов, например, каноническом числе реактивных элементов, когда их количество равно степени харак-

теристического полинома, задача синтеза становится однозначной в связи с ограниченностью реализаций, которые и образуют функционально полный набор схем данного типа. Эта задача решается на основе использования рассмотренных видов преобразований и их взаимных комбинаций с учетом перебора всех возможных значений преобразующих ПОЛИНОМОВ Хп Лр).

другая задача состоит в целенаправленном построении некоторой схемы без отыскания всего набора, в состав которого она входит. Такие схемы с идеальными активными приборами могут быть оптималь-

ны в смысле критерия минимальной чувствительности их параметров к изменению величин элементов схем, минимальной суммарной емкости конденсаторов или сопротивлений резисторов, благоприятных или определенных соотношений между величинами пассивных элементов, минимально необходимого коэффициента усиления активного прибора и др. Эта задача решается путем установления связи между полиномиальными коэффициентами заданной и преобразованной передаточных функций, т. е. определения целесообразного положения особенностей преобразованной функции на р-плоскости, которому соответствует определенный вид преобразующего полинома Хп,й{р)-

По промежуточным результатам синтеза схем с идеальными активными приборами можно сделать заключение о свойствах этих схем с реальными активными приборами и из группы схем, синтезированных при решении второй из указанных задач, отобрать ту, которая имеет, например, меньшую зависимость добротности от частоты, более широкую полосу рабочих частот, связанную с взаимной компенсацией частотных свойств реальных активныхприборов и другие полезные практические свойства.

Глава 6

УСТРОЙСТВА С ПРОСТЕЙШЕЙ ФОРМОЙ ПЕРЕДАТОЧНОЙ И ВХОДНОЙ ФУНКЦИЙ

1. масштабные усилители

К устройствам с простейшей формой передаточной функции относят масштабные усилители, интегрирующие и дифференцирующие цепи, а также другие типы цепей, передаточные свойства которых описываются дробно-рациональной функцией не выше первого порядка

/(p) = ( iP + o)/(biP + M. (6-1)

где Oi, о и t>i, Ьо -коэффициенты полиномов числителя и знаменателя.

Нули и полюсы функции (6.1) располагаются на действительной оси р-плоскости. Для устойчивой линейной цепи коэффициенты bt и Ьо могут быть только положительными, а коэффициенты О] и Со могут иметь как одинаковые, так и различные знаки.

При синтезе устройства по заданной схемной функции необходи- . МО знать возможность реализации функции при помощи цепей данного класса. Так как дальше рассматриваются схемы, содержащие пассивные элементы RC и активные приборы, то важно определить необходимые и достаточные условия реализации функции общего вида (6.1) в классе неуравновешенных (с общей стороной) пассивных цепей RC. Эти условия, известные как условия Фиалкова-Герста, состоят в том, что коэффициенты полиномов числителя ai и знаменателя bf должны быть положительными, причем коэффициенты щ меньше или, по крайней мере, равны соответствующи.м коэффициентам bi. Следовательно, если коэффициенты функции (6.1) удовлетворяют условиям

Oi > О, о > О, bi > О, Ьо >0; Оо < Ьо. 1 < Ьг, (6-2)