общие ресурсы поставщиков будут не меньше общего спроса потребителей:

z; i>i:bi- (7.80)

Ддя решения задачи (7.76) - (7.79) ее необходимо представить в канонической форме, т. е. ограничения (7.77), (7.78) записать в виде равенств. Это достигается, если

т п

Z i = 2:br (7.81)

1=1 3=1

в этом случае система ограничений будет совместна.

Для выполнения условия (7.81), в случае необходимости вводят фиктивный потребитель со спросом

т п

?=1 3=1

или фиктивный поставщик с ресурсом

п т

3=1 г=1

Если номер фиктивного потребителя k, то Cik=0. В этом случае груз x,ft рассматривают как фиктивную поставку . Если номер фиктивного поставщика s, то CgjO, /=1,п.

В дальнейшем предполагают, что условие (7.81) всегда выполняется, т. е. ограничения (7.77), (7.78) являются равенствами. Таким образом, модель транспортной задачи будет иметь вид: минимизировать

т п

S Z CijXij (7.82)

г=1 3=1

при ограничениях

п

Txij = ai, i=l,m; (7.83)

gXij = bj, j=l,n; (7.84)

Xij > 0, i l,m; j == T7n . (7.85)

Физический смысл ограничений (7.83) и (7.84) следующий: все Наличные ресурсы поставщиков должны быть вывезены и все потребности потребителей должны быть удовлетворены. Для заданного периода планирования требуется составить такой план перевозки груза, при котором общие транспортные затраты минимальны. Предполагается, что перевозится груз одного вида, так как задача перевозки грузов различных видов (многопродуктовая задача) сводится к рассматриваемой.

Транспортная задача (7.82) - (7.85) обладает следующими свойствами.

Для существования решения транспортной задачи необходимо

т п

выполнение условия баланса 2] г = 2] з-

В связи с этим одно из ограничений является линейной комбинацией всех других, т.е. ранг матрицы ограничений (7.83) -(7.84)

равен т+п-1. Если все щ, i=\,m, и Ь^, j=l,n, представлены целыми числами, то хотя бы одно из оптимальных решений будет целочисленным.

Допустимое решение транспортной задачи (план перевозок) записывается в виде двумерной матрицы, состоящей из т строк и п столбцов:

где Xij - количество груза (продукта), перевозимого от i-ro производителя j-y потребителю.

Допустимое базисное решение транспортной задачи называется ее опорным планом. План является опорным, если из ненулевых его перевозок нельзя составить замкнутый маршрут (цикл).

Опорность плана проверяется следующим образом. Просматривают последовательно строки, а затем столбцы плана X и вычеркивают те, которые содержат не более одной ненулевой перевозки. Весь процесс повторяют, пока после конечного числа вычеркиваний будет один из двух исходов: все строки (столбцы) вычеркнуты; получена подматрица, в каждой строке (столбце) которой содержится не менее двух ненулевых перевозок. В первом случае составить цикл из перевозок (коммуникаций) невозможно - план опорный. Во втором случае можно составить цикл из оставшихся перевозок - план не опорный.

Поставим в соответствие пунктам отправления и пунктам назначения вершины графа, а дорогам перевозок--дуги графа. Таким образом, множество вершин графа V={1, 2, т, т+1, т-\-п), а множество дуг графа L определим так, что {I, i)L, если из пункта i имеется дорога в пункт /.

Для получения транспортной сети поставим в соответствие элементам рассмотренного графа следующие параметры:

gs - количество единиц груза, которое имеется (g s>0) или потребляется (g s<0) в вершине s{s=\, т, т+1, т-\-п);

Уп - количество единиц груза, которое может быть перевезено из вершины (пункта) i в вершину (пункт) /, (i, ])зЬ, т. е. пропускная способность пути {i, j);

Cij - стоимость перевозки единицы груза из вершины i в вершину j (можно интерпретировать как длину пути).

Если Xij - искомое количество груза, перевозимое из пункта i в пункт /, то оно соответствует потоку для дуги {i, j) и удовлетворяет условию

0<Хгз<№з, (i./) sL. . (7.86)

Условие (7.73) также должно выполняться:

Hxij-JlXjigi, iV, (7.87)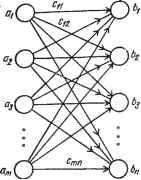

Рис. 7.2. Сеть транспортной задачи

Рис. 7.3. Исходная информация к транспортной задаче

Т. е. разность между количеством груза, отправленным из пункта (вершины) i, и количеством груза, пришедшим в этот же пункт (вершину), должна равняться интенсивности груза (потока).

Поскольку общие затраты на перевозку всех требуемых потребителями грузов равны

(7.88)

CijXij,

ТО задача (7.86) - (7.88) сводится к задаче об оптимальном потоке (7.73) - (7.75), т. е. классическая транспортная задача (7.76) - (7.78) свелась к задаче на сети при условии, что Xij=yij, {i,j)L. Если выполняется условие ХцкСУц, {i. j)L, то модель (7.86) - (7.87) описывает транспортную задачу с ограниченными пропускными способностями.

Таким образом, сеть транспортной задачи имеет вид, изображенный на рис. 7.2.

В сети транспортной задачи имеется т источников и п стоков. Исходная информация, необходимая для решения задачи, может быть записана в виде таблицы (двумерного массива), элементами которой являются стоимости перевозок с - единицы груза от i-ro поставщика к /-му потребителю; в последней строке записывается

спрос bj, j-\,n, в последнем столбце - наличные ресурсы щ, i=

= \,т (рис. 7.3).

Решение транспортной задачи методом потенциалов. Метод основывается на свойствах двойственности задач линейного программирования.

Двойственная задача к исходной транспортной задаче (7.82)- (7.85) описывается следующей моделью: максимизировать

m п

2 aiVi + Ц bjWj 1=1 j=i

(7.89)

при ограничениях

Vi + Wj < Cij, i =Л,т; j = l,n; (7.90)

Vi, Wj, t= 1, m; / = l,n - произвольные. (7.91)

Исходя из теоремы двойственности и теоремы о дополняющей нежесткости, можно утверждать, что если управляющие перемен-

ные Xij, i = \,т; j = l,n, исходной задачи удовлетворяют ограничениям (7.83) - (7.85) и управляемые переменные и° и двойственной задачи удовлетворяют ограничениям (7.90), а также выполняются условия

Xij{v4 -{-w°j - Cij) = О для всех i = 1, т; / = 1, /г, (7.92)

то управляемые переменные Xij, i=\,m; j=l,n, являются компонентами оптимального плана перевозок.

На основании изложенного разработаны алгоритмы решения сетевых задач, основанные на общей идее, что на каждой итерации для управляемых переменных Xij, Vi и Wj всегда выполняются два из следующих трех условий: допустимость исходной задачи, т. е. выполнение ограничений (7.83) - (7.85); допустимость двойственной задачи, т. е. выполнение ограничений (7.90); условия дополня-ющ;ей нежесткости (7.92).

В методе потенциалов (переменные Vi и Wj, i=\,m; j=l,n, двойственной задачи (7.89) - (7.91) называются соответственно потенциалами пунктов отправления и пунктов потребления) на каждой итерации выполняются первое и третье условия. Признаком оптимальности плана перевозок является выполнение третьего ус-, ловия. В рассматриваемой задаче предполагается, что ни в одном маршруте, соединяющем источник с некоторым стоком, другие источники и стоки не могут быть использованы в качестве промежуточных пунктов.

Метод потенциалов состоит в следующем. Имеется некоторый начальный поток (начальное допустимое базисное решение, начальный план), на основании компонентов которого определяются потенциалы вершин сети. Если выполняются условия v°-\-w°.-Cij =

=0, то начальный поток (план) оптимален. Если имеется (поток) дуга, для которой не выполняется условие оптимальности, то поток необходимо изменить, т. е. улучшить план перевозок. По измененному потоку определяются новые потенциалы, улучшается поток (план) и цикл повторяется, пока не будет выполняться условие оптимальности.

Таким образом, для реализации метода потенциалов необходимо уметь составлять начальный поток (план) и в случае необходимости улучшать его.

Рассмотрим построение начального плана (потока). Существует несколько методов построения начального плана (начального допустимого решения). Наиболее распространенными являются метод северо-западного угла и метод минимального элемента , в основе которого лежит метод сеееро-западного угла .

При методе северо-западного угла определяется значение хц, т. е. максимально допустимый поток для маршрута, соединяюшего первый источник с первым стоком:

Хц - min{ai,fci}.

Если й! = bi, то удаляются источник 1 и сток 1 и выбирается для определения Х22, т. е. маршрут, соответствующий Х22.

Если ai>bi, то удовлетворяется спрос стока, т. е. Xu = bi, сток удаляется и выбирается маршрут, соответствующий Xi2.

Если ai<:bi, то предложение источника реализовано полностью, сток не удовлетворен, т. е. A:ii=ai, удаляется источник и выбирается маршрут, соответствующий Х21.

Таким образом, для выбранного маршрута определяется максимально допустимый поток и удаляется либо источник, если его предложение реализовано полностью, либо сток, если его спрос удовлетворен. Если одновременно выполняются условия на пред-лом^еиие и спрос, то удаляются и источник и сток. Аналогично повторяется процедура для определения всех потоков Xrs, т. е.

Xrs = min {aW, bf)}, (7.93)

s-l r-1

где af) == - 2] rj, b(> ~ bs - 2 xis, k - номер итерации.

Ha следующей итерации выбирается переменная Xr,s+u если предложение г-го источника реализовано не полностью, переменная Xt+\,s, если спрос s-ro стока удовлетворен не полностью, и Хг+\, S+1 - в противном случае.

При построении начального опорного плана (выборе маршрута) методом минимального э лемента используется информация о транспортных издержках С = llcijll.-

В матрице издержек С - \\cij\\ нумеруются элементы в по-

рядке их возрастания. Опорный план X заполняется перевозками в последовательности полученной нумерации по правилам, аналогичным методу северо-западного угла .

Рассмотрим правила улучшения начального опорного плана.

Пусть имеется некоторый поток (план) и пусть М{Х) - множество дуг, для которых Xij>0:

М{Х) - {(/,/): >0}.

Опорой потока X={Xij} называется частичный граф {V, М{Х)). Поток X={Xij) невырожден, если его опора (У, М{Х)) является связным графом (все элементы ха>0). В случае вырожденности необходимо незначительно расширить исходную сеть, добавив маршрут с бесконечно малой перевозкой е так, чтобы потоку х(е) в новой сети соответствовал уже связный частичный граф. Для этого в каждой компоненте связности выбирают произвольную вершину-источник и уменьшают ее интенсивность на бесконечно малую величину е. После этого вводят фиктивную вершину с интенсивностью, равной суммарной интенсивности, на которую была

уменьшена интенсивность выбранных вершин. Фиктивную вершину соединяют с каждой из выбранных дугой с нулевым значением стоимости перевозки. Опора любого потока хц{е) в новой сети будет связным графом.

Таким образом, для устранения вырождения достаточно соединить компоненты связности опоры нулевыми потоками. . Введем замену переменных; vt = -щ, i=l, т. Тогда для оптимальности плана перевозок X=IUij необходимо и достаточно существование потенциалов Wj, j=\,n, пунктов потребления и потенциалов i~Ui), i=l, т, пунктов поставок таких, что

Wj - Uidj, i=\,m; j=l,n.

Для перевозок Xij>0 в силу теоремы о дополняющей нежесткости должны выполняться условия:

для всех Xij>0 обязательно Wj-щ-с^. (7.94)

Разность Wj-щ можно рассматривать как приращение ценности единицы продукции при доставке ее из пункта отправления в пункт потребления. В связи с этим, если Wj-щ^сц, то перевозка из пункта i в пункт / нерентабельна и должна отсутствовать, т. е. Xij=0. В противном случае перевозка рентабельна, т. е., если Wj- -Ui=cij, то Xij>Qi.

Поскольку рентабельность зависит только от разности между потенциалами Wj и щ, то, положив, например, щ^- {io - начальная вершина сети), можно вычислить потенциалы вершин сети пй формулам Wi=Ui-]-Cij, Ui=Wj-Cj-j в силу связности графа {V, М{Х)).

Если для начального потока X-{Xtj} будет выполнено условие.

Cij - {Wj -Ui)-0, (7.95)

то поток (план перевозок) является оптимальным. В противном случае план (поток) надо улучшить. Пусть для некоторой дуги {г,1)М{Х) условие (7.95) не выполняется. Из условия построения потенциалов каждой вершины следует, что существует цепь [to, ii,is=i], ведущая из вершины io в вершину г, вдоль которой был определен потенциал Us, и существует цепь [io,-.i(.-., i - ведущая из вершины io в вершину /, вдоль которой был определен потенциал Wj. Частично эти цепи могут некоторыми вершинами совпадать.

Построим цикл. Для этого соединим указанные две цепи ребром [г, /] и получим цикл

I = [io, ii,is = f, i+i = I, it = io]-

Направление дуги (г, /) должно определять направление обхода полученного цикла.

Пусть М+ и М- - множества дуг, ориентированных в направлении обхода этого цикла и соответственно в противоположном.

Построим улучшенный поток Х' - {х'}.} по правилу

Xij + е при (/, /) е Mf; Xij - е при (г, /) е Жб ; (7.96)

.Xij при {i,j)eMi[jM, где

в = min {minXij, min (-Xij)}.

Разность между потоком, входящим в любую вершину, и потоком, выходящим из этой же вершины, при преобразовании (7.96) н изменится. Следовательно, поток (план) Х> = {х'.} будет выгоднее предыдущего потока X = {Xij} сети:

2 CijXj - 2 CijXij = е{ 2 - 2 Cij} =

== 0 (Що - Ui, + Ui,-----Ur - Cri+Wi- Wi+i -f Wi-i----

----WiJ = @{Wi - Ur - Cri) > 0.

Если для полученного потока условие оптимальности не выполняется, то определяем новые потенциалы и улучшаем этот поток. Процедуру улучшения потока повторяем до тех пор, пока поток не станет оптимальным. Оптимальный поток соответствует оптимальному плану перевозок, т. е. решению задачи.

Рассмотрим транспортную задачу с ограниченными пропускными способностями.

Если на пропускную способность путей накладываются ограничения, то имеет место транспортная задача с ограниченными пропускными способностями. Такая задача описывается моделью (7.82) - (7.85), в которой ограничения (7.85) имеют вид

О < Xij < yij, i --- 1, m; / = 1, п.

В этом случае, чтобы поток Х={х } был оптимальным, необходимо и достаточно существование для каждой вершины iV такого потенциала щ, что

Wj - а, < Cij, если Xij = 0;

Wj - щ = Cij, если О < Xij < yij; (7.97)

Wj - Ui Cij, если Xij = yij.

После определения потенциалов по правилам, рассмотренным в предыдущем случае, при невыполнении условий (7.97) возможен один из трех случаев:

Wi - Ur> Cri при Xri = 0;

Wi - и ф Cri при о < Xri < Уг1, Wi - Ut< Cri при Xrl = Уг1-

Тогда улучшенный поток определяется по правилу (7.96),. но величина в - по формуле

в = min { min х^, min (Уц - Хц)},

(г,з)еЛГ- (г,з)еЛГ+

при этом выполняются условия

0<х%уп, еЖ.

Многие транспортные задачи включают пункты для перевозки грузов (пункты распределения, склады, оптовые базы и т. п.). В этом случае требуется отыскать план перевозок грузов, минимизирующий транспортные затраты при любой заданной схеме размещения перевалочных пунктов, т. е. рассматривается транспортная задача с промежуточными пунктами. Такую задачу также можно описать сетью, в которой вершины соответствуют источникам (пунктам поставки), стокам (пунктам потребления) и промежуточным пунктам (складам и т. п.).

Поскольку у источников имеется избыток груза, который необходимо вывезти, то соответствующая вершина характеризуется положительным числом, равным количеству вывозимого груза. Сток потребляет груз, и соответствующая вершина характеризуется отрицательным числом, равным количеству требуемого груза. Вершине, соответствующей промежуточному пункту, приписывается положительное число, обозначающее избыточное количество запаса груза или отрицательное число, обозначающее потребность в дополнительном грузе.

Задача с промежуточными пунктами легко сводится к классической транспортной задаче.

Для каждого промежуточного пункта k определяется чистый запас груза Sh. Если в k-u пункте имеется избыток запасов, то запас Sft должен быть положительным; если в k-м пункте требуется пополнение запасов, то должен быть отрицательным числом.

Пусть а - фиктивный запас груза в каждом промежуточном пункте, т. е. запас, равный суммарному запасу, имеющемуся-во всех пунктах. Для любого пункта k выполняются соотношения:

flft = Sft -f а; bh = а.

Для промежуточного пункта k вводится переменная потока Хии при стоимости перевозки единицы груза 6-=0. При таком построении условие баланса не нарушается. Сумма всех а, остается равной сумме всех bj. Значение аи должно быть настолько велико, чтобы оно могло включить любое количество груза, проходящего через промежуточный пункт в оптимальном режиме. Для этого запас а берется равным сумме запасов, имеющихся во всех пунктах. Поэтому разность а-xh является общим количеством груза, перевезенного через промежуточный пункт k.

Задача о максимальном потоке

Пусть имеется сеть G{V, L) с ограниченными пропускными способностями дуг, в которой один источник (вершина 0) и один сток (вершина р+1)- Требуется определить максимальный поток из источника в сток для этой сети.

Математическая модель задачи имеет вид: максимизировать / (7.98)

при ограничениях

xui = f, k = 0; (7.99)

Z Xui - TiXik = Q, k=l, p; (7.100)

-Exi.p+i = -f, k-P+U (7.101)

0 < Xij < yij, (t, /) e L, yij > 0, (7.102)

где I - интенсивность источника (вершина 0); -/ - интенсивность стока (вершина p+l).

Максимальным является поток, для которого интенсивность / удовлетворяет соотношениям (7.98) - (7.102). Максимальное значение / называется максимальным потоком из источника О в сток Р+1.

Пусть SczV и OeS, p-f-leS. Разрезом сети, отделяющим источник О от стока р--1, называется множество дуг

1(8) = iS,S) = {{i,j) :iS, jS}.

Сумма пропускных способностей таких дуг y{S,S) называется величиной разреза. Минимальным является разрез, у которого наименьшая пропускная способность.

Максимальный поток из источника О в сток р--1 равен пропускной способности минимального разреза, отделяющего источник О от стока р+1.

Если дуга (i, /) входит в минимальный разрез, то максимальный поток по дзге (i, /) равен пропускной способности у,-, этой дуги.

Вводится фиктивная дуга (О, р+1), обладающая неограниченной пропускной способностью Уо, р+1 = оо.

Предполагается, что функция стоимости

hi = 0,j = p+U j3

Cij =

0,i¥=0, j¥=p- 1.

Если поток Хо, p+i минимальный, то через остальные дуги пройдет максимальное количество потока.

При Хо, р+1>0 разность Wp+i- о= 1 (где Wp+i и о - потенциалы стока р-[-1 и источника О соответственно) по условиям теоремы двойственности. Потенциал одной из вершин может быть взят равным нулю, например Uo=0.

Двойственная задача к задаче минимизации потока: максимизировать

/- Z гпуц (7.1.04)

(i,3)sG

при ограничениях

Wj - Ui - Zij < О, (i, /) е G; (7.105)

0 = 0, mp+i=l. (7.106)

Решение этой задачи следующее. Максимальный поток хР.. должен удовлетворять условиям

ьуо - о О при О < А . < yij.

Поэтому все потенциалы и zn равны О или 1. По теореме двойственности

Xo,p+i f - Е г}Уп = f- Е У а, (7.107)

где = {{i,j): Zij = 1}.

Из (7.107) следует, что максимальный поток равен Eytj-

Любой путь от источника к стоку содержит дугу, входящую в разрез; Lz является разрезом, так как если бы существовал путь от О к р+1, не содержащий элементов Lz , то, увеличивая пропускные способности всех дуг, входящих в этот путь, можно было бы увеличить поток. Но z°..= О при (t,/) е La, Поэтому увеличение

пропускной способности всех дуг, не входящих в Lz°, не изменит значений целевой функции двойственной задачи (7.104), а также максимального потока. Так как максимальный поток не больше, пропускной способности любого разреза, то разрез Lz является минимальным.

Приведем алгоритм определения максимального потока.

Ш а г 1. Определить путь из источника О в сток р+1, по которому, поток принимает положительное значение. Если такого пути нет, перейти к шагу 3.

Шаг 2. Определить в = min {(/ij) > О, вычесть в из всех уц для пути из О Б p-f-1 и прибавить в ко всем уц для пути из р+1 в 0. Перейти к шагу 1. Эта операция позволяет использовать оставшиеся пропускные способности и восстанавливает исходные пропускные способности, так как уменьшение пропускной способности в одном направлении увеличивает пропускную способност.л в противоположном направлении.

Ш а г 3. Определить оптимальный поток X = \\хц\\, где

Уи - У*., Ун > У*.;

(7.108)

О, УнУ*:,

Xij =

максимальный поток

Здесь {/ij-- исходные пропускные способности; {/*-пропускные способности дуг,

полученные на шагах 1 и 2.

Таким образом, максимальный поток f равен сумме всех положительных 0. Пусть yij = 1 для всех (i, /) s L.

Рассмотрим любой допустимый поток. Является этот поток максимальным или возможно его увеличение?