-гпртьего - b, единиц. Известно, что в единице сырья Sj содержится ci,- единиц первого компонента, единиц второго компонента и единиц третьего ком-понента (/ К 2, 3, 4).

Требуется так произвести бетон, чтобы его стоимость была минимальной при выполнении заданных условий.

Решение. Пусть Xi, хч, х^, х^ обозначают искомые количества сырья видов Si, Sz, 5з, 54, входящих в бетон.

Общая стоимость бетона

Запишем условия содержания в бетоне каждого из компонентов. Если в одной единице сырья вида S, содержится первого компонента ац, то в х, единицах- ЧцХи в Хг единицах сырья вида - а^х^ и т. д. Общее количество первого компонента в бетоне не должно быть меньше bi; математически это условие запишется в виде неравенства

сцХ] -f 0,2X2 + 013X3 4- 014X4 > bi.

..налогнчно записываются условия для других компонентов:

ОцХ, + 012Х2 + aisXa + 144 > bi;

021Х, + 022Х2 + О23Х3 + 024Х4 > bi, (7.12)

031Х, -f O32X2 + 033X3 + O34X4 > Ьз.

Эти неравенства являются ограничениями, накладываемыми на искомое решение задачи Xi, Хг, хз, Х4.

Таким образом, возникает следующая задача: найти такие неотрицательные значения переменных Хь Хг, Хз, Х4, удовлетворяющие линейным ограничениям, при которых линейная функция (целевая функция) этих переменных обраща-лась бы в минимум:

LCjXj-min. (7.13)

3 = 1

Соотношения (7.12)-(7.13) описывают математическую модель сформулированной задачи.

Пример 2. Цех столярных изделий домостроительного комбината располагает Ni станками типа 1, N2 станками типа 2. Станки могут производить столярные изделия четырех видов: щ, щ, щ, щ.

Станки каждого типа могут производить столярные изделия любого вида, но в неодинаковом количестве.

Станок типа t (t = 1,2) производит в месяц ац единиц изделий U\, ац - изделий 2, 0.П - изделий Ыз, 0,4 - изделий щ.

Каждая единица изделия ы, приносит цеху доход Ci, изделия Ы2 - доход Сг, изделия Ыз - доход Сз, изделия Ы4 -доход С4. Цеху предписан план, согласно которому он обязан произвести за месяц- не менее Ь, изделий щ, не менее Ьг изделий Ы2, не менее Ъз изделий Ыз, не менее 64 изделий щ.

Требуется так распределить загрузку станков производством изделий различных типов, чтобы план был выполнен и при этом месячная прибыль была максимальной.

Решение. Запишем условия задачи математически (построим математическую модель задачи). Обозначим Хц - число станков типа 1, занятых производством изделий Ы], Xi2- число станков типа 1, занятых производством изделий ыг, т. е. Xj, - количество станков типа i, занятых производством изделий ы,-. Первый индекс соответствует типу станков, второй - типу изделий (г =1,2; / = = 1. 2. 3, 4).

Таким образом, необходимо определить восемь переменных:

Хц, Xi2, Xi3, Х14; Х21, Х22, Х23, Х24

так, чтобы месячная прибыль была максимальна.

Запишем формулу для вычисления этой прибыли. Так как каждое изделие 3. / = 1,2,3,4, приносит прибыль с,-, то x,j изделий принесут прибыль CjXij.

Поскольку станок типа 2 тоже может производить изделия Uj, то изделие Uj принесет цеху прибыль

Ci{Xij + X2i).

Общая прибыль

L = с, (Хп + Х21) + С2(Х,2 + Х22) + Сз(Х,з4- X2s) + £4(14 + Xzi). (7.14)

Требуется определить такие неотрицательные значения переменных Хц, i = = 1,2; /= 1,2,3,4, чтобы линейная функция от них (7.14) обращалась в максимум. При этом должны выполняться следующие ограничения:

1) ресурсы по станкам не должны быть превышены, т. е. сумма количеств станков каждого типа, занятых производством изделий всех видов, не должна превышать наличного запаса станков:

Xii+Xi2 + Xii + XnNi; X2,+X22 + X23 + X24 <N2; (7.15)

2) задания по ассортименту должны быть выполнены (или перевыполнены);

ацХп + 021X2, > Ьй ОцХп + a2iX2s >

01212 + Й22Х22 bi, ацХц + ацХц > 64. (7.16)

Сформулируем задачу: определить такие неотрицательные значения переменных Xij, i= 1,2; /= 1,2,3,4, при которых их линейная функция (7.14) обращается в максимум и выполняются ограничения i(7.15), (7.16).

Решения Х= (х Хг, Хп), удовлетворяющие ограничениям (7.4)-(7.7), называются допустимыми решениями модели и образуют допустимое множество (область) решений. Допустимое решение, максимизирующее (минимизирующее) целевую функцию (7.3), называется решением задачи линейного программирования (оптимальным планом).

Задача, описанная моделью (7.3)-(7.7), может не иметь ни одного допустимого решения или может иметь: единственное допустимое оптимальное решение; несколько допустимых оптимальных решений; такое допустимое решение, для которого целевая функция является неограниченной, т. е. неограниченно возрастает для задачи максимизации и неограниченно убывает для задачи минимизации.

Для решения задачи (7.3-7.7), казалось бы, можно применить метод простого перебора: найти произвольное допустимое решение Х<-\ вычислить значение целевой функции fo(XW), затем найти следующее допустимое решение Х'-\

вычислить для него fo(X<2)), сравнить fo(X( )) с foiX)), запомнить лучшее значение fo и соответствующее допустимое решение; такую процедуру повторять

для всех возможных допустимых решений. Значение Х= (х .... Хп), при котором /о(-) примет максимальное (минимальное) значение, будет решением задачи линейного программирования. Но в силу сложности поиска и невозможности перебора всех допустимых решений такой путь нереализуем.

Допустимое множество решений задач линейного программг-рования всегда является многогранным и непустым множеством, если система ограничений (7.4) - (7.7) совместна, т. е. обладает хотя бы одним решением. Если допустимое множество решений не пусто, то оно является выпуклым многогранным множеством. Поэтому задача линейного программирования представляет собой отыскание максимума (минимума) линейной функции на многогранном выпуклом множестве. С геометрической точки зрения решению задач линейного программирования соответствует одна из вершин множества допустимых решений. Поэтому отыскание решения задачи (7.3) - (7.7) сводится к перебору конечного числа вершин выпуклого многогранного множества.

Для наглядности рассмотрим задачу линейного программи-

рования с т ограничениями и двумя управляемыми переменными:

тгх {CiXi +С2Х2); (7.17) anXi + ai2X2aio ] ...... (7.18)

ClmlXi -j- Clm2X2 j

XuX2>0. (7.19)

Пусть система (7.18) совместна и соответствующая область допустимых решений ограничена, т. е. является многоугольником. Каждое из ограничений (7.18) определяет полуплоскость соответственно с граничной прямой ацХ1-\-Щ2Х2=а{о, t=l, т.

Если функцию цели приравнять некоторой константе 5, то получим тоже уравнение прямой

CiXi -f С2Х2 =

Jмeняя константу получаем семейство параллельных прямых - линии уровня целевой функции.

Пусть область допустимых решений (выпуклый многоугольник) D и линии уровня целевой функции соответствуют рис. 7.1.

Если прямую CiXi-j-C2X2-t перемещать в направлении ее нОр-мали C={ciC2), то значение будет неограниченно возрастать. Линии уровня вначале могут не иметь общих точек с областью D, а затем при некотором прямая CiX\-{-C2X2=i, коснется области D (точка Л^), потом пересечет ее и, наконец, коснется ее в последний раз в точке М; в этой точке функция цели достигнет своего максимального значения.

Если область допустимых решений представляет неограниченный многоугольник, то может быть один из двух случаев: прямая CiX\-{-C2X2=t передвигаясь по нормали, все время пересекает область D или становится опорой к ней. В первом случае целевая функция неограниченно возрастает, во втором - достигает своего максимального значения.

Таким образом, можно утверждать, что целевая функция достигает своего максимального значения в вершине многоугольника (угловой точке). Вершины области допустимых )ешений называют экстремальными точками. 1сш целевая функция достигает максимального значения более, чем в одной точке, то она достигает этого же значения в любой точке, являющейся их выпуклой комбинацией (прямой, соединяющей эти экстремальные точки).

Следовательно, чтобы решить задачу линейного программирования, необходимо рас- Грпмртпи сматривать только решения, соответствующие .J интерпре?а-угловым точкам области допустимых решений. задачи линейно-В связи с этим необходимы правила, следуя го программирования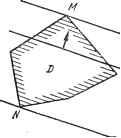

которым можно определять угловые точки и целенаправленно переходить от одной угловой точки допустимой области к другой.

Каноническая форма задач линейного программирования

Существующие методы решения задач линейного программирования применимы к моделям этих задач, представленным в канонической форме, которая характеризуется следующими тремя признаками:

система ограничений представлена в виде системы уравнений;

на все переменные накладываются условия неотрицательности;

производится максимизация (минимизация) целевой функции.

В канонической форме общая задача линейного программирования имеет вид: максимизировать

h = t с,х, (7.20)

при ограничениях

ОгЛ- = го, i - hm; (7.21)

х,>0, /=1,п, (7.22)

где Cj, Cij, ttio - заданные постоянные величины; Xj - искомые управляемые переменные.

Задача (7.3) - (7.7) переводится в каноническую форму (7.20) - (7.22) путем преобразования всех ограничений, имеющих вид неравенств, в равенства. Это достигается добавлением неотрицательных остаточных переменных в левую часть неравенств (7.5) и вычитанием неотрицательных переменных в левой части неравенств (7.6). Ограничения (7.5) и (7.6) примут вид:

ar+i,iXi + r+i,22 Н----+ar+i,nXn+ l-Xn+i = ar+i,o,

tir+2,lXl + Cir+Z,2X2 + + a.r+2,nXn + 0-X +i -j- 1 Xn+2 - Cir+2,o,

anXi + ai2X2 -I----+ ainXn+ 0-a: +i -f----[-О-Хп+ц-ц + l-Xn+i = aio,

Ог+1, li + Gj-(-l,22 + + 0,l+l,nXn- 1 -Xn+l+l = Gj-H,o;

fi!m, 1-1 + 2-2 + + ai+z, nXn - 0 - 1 Xn+i+z - ai+z, c;

OmlXi + m22 H----+ ClmnXn - 0-Xn+l+i----

... 0-Xn+l+m~l -1 -Xn+m = Ctmo-

Таким образом, для приведения задачи (7.3) -(7.7) к каноническому виду необходимо ввести в ограничения (7.5) -(7.6) т-г свободных переменных, из которых /-г - остаточные переменные и т-/ - избыточные переменные. Целесообразно также сделать неотрицательными все элементы правой части ограничений Що- При

наличии переменных, которые не удовлетворяют условиям (7.7), необходимо вместо переменной Хр ввести в модель две неотрицательные переменные х+ и х-:

Хо = х+-- Х-. р р

В результате преобразования модели (7.3) - (7.7) к канонической форме (7.20) -(7.22) количество управляемых переменных Xj возрастет.

Задача минимизации может быть сведена к эквивалентной задаче максимизации и наоборот, если одновременно с изменением знака оптимизации изменить знаки перед всеми коэффициентами

п

В выражении для целевой функции, т. е. минимизация 2] cXj экви-

П 3=1

валентна максимизации 2] {-Сз)Х]. При этом

п п

min 2] CjXj = max 2] (-Cj) Xj.

3=i 3=i

Приведенную к канонической форме модель задачи линейного программирования часто удобно рассматривать в матричном или векторном представлении.

Матричное представление модели: минимизировать (максимизировать)

Хо = СХ (7.23)

при ограничениях

АХ = Ао; (7.24)

Х>0, (7.25)

где Х== {Xi,Хп) - вектор, компонентами которого являются управляемые переменные (в число этих ко мпонентов могут входить -остаточные и избыточные переменные); Ао= (а\о, Ото) - вектор, компонентамикоторого являются неотрицательные правые части ограничений; А = \\ац\\тхп - матрица коэффициентов ограничений, включающая коэффициенты при остаточных и избыточных переменных.

Векторное представление модели: максимизировать (минимизировать)

при ограничениях

Z сл- (7.26)

2] AjXi = Ао; (7.27)

Xi>0, /=- (7.28)

где А= (Аи А2,... An). Векторы Aj и Ао часто называют векторами условий.

Обычно количество ограничений (7.27) меньше количества управляемых переменных, т. е. т<Сп. Если т>п, то система ограничений содержит по крайней мере т-п избыточных уравнений;

если т=п и А - матрица^юлного ранга (все ограничения линейно независимы), то система ЛХ==Ло имеет единственное решение.

В случае m<Zn система АХ=Ло имеет бесконечное множество решений; если эта система несовместна, задача не имеет ни одного допустимого решения.

Допустим система совместна, выберем из матрицы A={Ai,..., Ап)т линейно независимых векторов, обозначив матрицу, содержащую их, через л™х™. Эта матрица образует базисе системы. Матрица А может быть представлена в виде A-{B,N), где N~ матрица, содержащая небазисные векторы.

Ограничения (7.24) перепишутся так:

ВХв + NXn = Ао, (7.29)

где Хв - вектор базисных переменных, связанных с матрицей Б; Xn - вектор небазисных переменных, связанных с матрицей Л'. Так как В - невырожденная квадратная матрица, то существует обратная матриц В-. Выразим базисные переменные через небазисные, умножив обе части соотношения (7.29) на В~:

В-тХв + B-NXn = В-Ао.

Так как Л-Ш=1, получим

Хв = В-Ао - (7.30)

Соотношения (7.30) определяют полное множество решений системы линейных уравнений (7.24).

Небазисные переменные могут принимать произвольные значения. Пусть все небазисные переменные принимают нулевые значения, тогда базисное решение

Хв = В-Ао. (7.31)

Если базисное решение ХвО, то оно называется допустимым.

Если все базисные переменные вектора Хв строго положительны, то базисное решение является допустимым невырожденным. Если хотя бы одна переменная вектора Хв равна нулю, допустимое базисное решение называется вырожденным.

Количество экстремальных точек определяется числом сочетаний

Qn - -.

п т\{п - т)\

Т. е. количеством допустимых базисных решений системы АХ = = 11 AjXj = Ао. Невырожденному допустимому базисному реше-

нию соответствует невырожденная экстремальная точка, а вырожденному - вырожденная. Невырожденная экстремальная точка определяется только одним базисным решением, вырожденная - двумя и более.

Симплекс-метод решения задач линейного программирования

Основнаяидея симплекс-метода заключается в целенаправленном последовательном нахождении экстремальных точек с помощью допустимых базисных решений системы ограничений. Этот упорядоченный процесс начинается с некоторой начальной экстремальной точки (исходного допустимого базисного решения) и продолжается до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

В качестве каждой новой экстремальной точки (допустимого ёазисного решения) выбирается смежная с предыдущей экстремальная точка, в которой, по крайней мере, не ухудшается значение целевой функции. Обратный переход к предшествующей экстремальной точке невозможен. Поэтому в процессе вычислительной процедуры после определения нового допустимого базисного решения предыдущее исключается. Максимальное количество итера-х^ереходов к смежным экстремальным точкам) не превышает С™ [п - количество переменных, am - количество ограничений задачи (7.20) -(7.22)].

Смежные экстремальные точки отличаются только одной переменной. Поэтому каждую последующую экстремальную точку определяют заменой одной из текущих базисных переменных новой из числа небазисных.

Таким образом, симплекс-метод предполагает следующие процедуры:

1. Определение начального допустимого базисного решения. Это решение получается приравниванием нулю п-т небазисных переменных. Исключение из выражения для целевой функции базисных переменных.

2. Определение из числа небазисных переменных переменной, которая должна быть включена в число базисных переменных. Эта новая базисная переменная должна улучшить значение целевой функции.

3. Определение из числа базисных переменных переменной, которая должна быть исключена из базисного решения, т. е. заменена новой базисной переменной.

Две последние процедуры повторяются до тех пор, пока возможно улучшить значение целевой функции.

Определение начального допустимого базисного решения осуществляется просто, если в ограничениях (7.24) имеется единичный базис, т. е. они имеют вид:

AXn + ЕХв = Ло; (7.32)

Xn>Q, Хв>0, . (7.33)

где Е - единичная матрица.

Такой вид имеют ограничения (7.24), если при переводе модели задачи в каноническую форму в каждое ограничение была введена остаточная переменная.

Если при переводе модели задачи в каноническую форму в каждое ограничение были введены избыточные переменные или некоторые ограничения исходной модели имели вид равенств, то для приведения ограничений к виду (7.32) в них вводят искусственные переменные таким образом, чтобы организовать единичную матрицу Е. Так как в исходную задачу (7.23) -(7.25) искусственные переменные не входят, то в оптимальном решении задачи они должны равняться нулю. Это условие достигается введением в исходную целевую функцию искусственных переменных с коэффициентами, принимающими большие значения, т. е. введением больших штрафов . Так преобразованную задачу называют М-задачей.

Пример:

max (Зх, - Х2 -Ь 2хз -Ь Х4); 4х, -Ь Хг - 2хз = 4; 2х, -Х2 4-4x3-1-Х4= 10; х, > О, Х2> О, ХзЖС Х4> 0. -Зх, + 2X2 + Хз- 2X4 = 8; Введя три искусственные переменные уъ yt, уз, получим М-задачу: max (Зх, - Х2 -Ь 2хз -f- Х4 - Л1</, - Му2 - Муз); 2xi - Х2-Ь 4хз-Ь Х4-I-1-i/i = 10; -Зх, + 2x2 + Хз - 2x4 -Ь 0-i/i -Ь 1 -2 = 8; 4х, -ЬХ2 - 2хз -Ь 0-Х4 + 0-У1 + 0-У2 +1-Уз = 4;

Xi>0, Х2>0, ХзО, Х4>0, У1>0, У2>0, </з>0.

Предполагается, что М > с,-, / = 1, 4; Л1 > 0. Начальное допустимое базисное решение: yi =

10; у2 = 8; </з = 4.

Таким образом, в случае ограничения вида (7.32) начальное допустимое базисное решение имеет вид

Хв = Ао.

Новая базисная переменная определяется по симплекс-критерию: если в выражении для целевой функции (после исключения базисных переменных предыдущей итерации) имеются небазисные переменные, за счет которых можно увеличить значение целевой функции, то в базисное решение вводится та переменная, которая дает наибольшее приращение целево функции (задача максимизаци^). Е^ли базисные переменные Хв выражены через небазисные Хв=В-Ло-B~NXn, которые исключены из выражения целевой функции, то целевая функция примет вид

Хо = СвВ-Ао - {CbB-N - Cn) Xn, (7.34)

где Св и Cjv - векторы, компонентами которых являются соответственно коэффициенты целевой функции при базисных и небазисных переменных.

Так как небазисные переменные Xn==0, то каждая итерация имеет допустимое базисное решение

Хв = В-Ао,

а целевая функция

Хо = СвВ-Чо.

Очевидно, что значение целевой функции может быть увеличено

п ча счет той переменной, для которой выражение (CbB-N-Cn) будет отрицательно. Поэтому в новый базис необходимо включать тот вектор Aj (ввести новую базисную переменную Xj), для которого разность

CbB-Ij - Cj (7.35)

имеет наибольшее отрицательное значение. Если такого вектора нет, то полученное допустимое базисное решение является оптимальным. Выражение (7.35) называется симплекс-разностью.

Чтобы выделить в текущей матрице условий единичную подматрицу, т. е. выразить все базисные переменные через небазисные, пользуются методом полного исключения Жордана - Гаусса. Этот метод основан на эквивалентных преобразованиях системы уравнений с целью разрешения на каждом шаге одного уравнения относительно одной неизвестной (базисной переменной) и исключения ее из всех остальных уравнений, что приводит систему к единичному базису, состоящему из единичных векторов-коэффициентов.

П- -менная, выводимая из базиса, определяется из условия, что базис должен все время оставаться допустимым, и при вводе в базис новой переменной одна из его переменных должна принять значение, равное нулю. Поэтому из базиса должен быть выведен вектор Ai, для которого справедливо соотношение

(B-Ao)i

- - mm

г

iB-Ao)i

{B-j)i > О

(7.36)

где {В~Ао) г.-1-й компонент вектора В-Ао,. 1= 1, пг.

Если все {B-Aj)iG, то выбор Aj для ввода в базис не может привести к допустимому базисному решению.

Реализовать симплексный метод решения задач удобно в виде таблиц, заполняемых на каждой итерации в соответствии с симплексными преобразованиями, которые являются модификацией метода полного исключения Жордана - Гаусса.

Таблица 7.1

Алгоритм решения задачи методом симплекс-таблиц содержит следующие этапы:

1. Заполнение исходной таблицы параметрами, соответствующими начальному допустимому базисному решению (табл. 7.1). Такими параметрами являются: базисные переменные хи iI, где / - множество индексов базисных переменных (столбец Вх); ба-зисные переменные Що (столбец Ло); элементы матрицы А= - WctijWm.n, содержащей допустимый единичный базис (столбцы Аи -2,.... Л„); коэффициенты целевой функции (строка С); коэффициенты целевой функции при базисных переменных (столбец С); оценки векторов условий (симплекс-разности)

= aoj = Е Сгйц - Cj, j g /, (7.37)

где Д - индексная строка; Ооо - целевая функция: аоо=2сгаго.

Если все AjO, то данное допустимое базисное решение является оптимальным; если Ак<0 и все элементы столбца AkO-ikO,

i=l,m, то задача неразрешима; если в каждом столбце А^, для которого Aft<;0, имеется хотя бы один положительный элемент, то возможен переход к новому допустимому базисному решению, более близкому к оптимальному. В последнем случае осуществляется переход ко второму этапу.

2. Выбор вектора Ар, вводимого в базис, из условия

Ар = аор ;= min [uoi \ < 0). (7.38)

3. Выбор вектора Aq, выводимого из базиса, из условия

Ото

- = min

OrpX)

(7.39)

4. Осуществление одного шага симплекс-преобразования с направляющим элементом йдр, для чего используют формулы:

(ft)

T=- = 0.1.:...,n; (7.40)

4+ О, Г 1, 2,т; гфд; = 1; (7.41)

(ft)

а}Г' = aS-.- ,Л Ф р, г Ф q, (7.42)

где k - номер итерации (симплексного преобразования). Элементы индексной строки новой таблицы вычисляют тоже по соотношениям (7.40) -(7.42).

Правильность вычислений элементов индексной строки контролируют по формулам:

dm = I] Cittio ; (7.43)

Chi = I] Сгйц -Си (7.44)