налы либо дискретные, причем длительность дискретных сигналов обычно значительно превышает длительность сигналов управляю-шей информации. В связи с этим система связи ЭВМ с объектом управления должна содержать технические средства, запоминающие управляющую дискретную информацию до замены ее новой информацией или формирующие управляющие воздействия, воспринимаемые входами исполнительных устройств.

Связь ЭВМ с объектом в системе автоматического управления может быть синхронной, асинхронной и комбинированной.

При синхронной связи процесс управления с помощью тактовых сигналов устройства текущего времени (УТВ) разбивается на циклы одинаковой продолжительности. Каждый цикл начинается с появлением тактового сигнала на входе блока прерывания. Вначале цикла осуществляется последовательный опрос датчиков, контролирующих состояние объекта управления. Сигналы датчиков преобразуются в форму, необходимую для ввода этих сигналов в ЭВМ. Поступившая в ЭВМ информация обрабатывается и выра-

:.1заются требуемые управляющие воздействия на объект, которые после соответствующего преобразования в системе связи ЭВМ с объектом передаются на исполнительные устройства. Затем ЭВМ либо останавливается, либо выполняет другие программы, не связанные с системой автоматического управления. Выполнение этих программ прерывается следующим тактовым сигналом УТВ. Управляющие воздействия, сформированные в начале цикла, остаются неизменными в течение всего цикла.

При асинхронной связи с объектом ЭВМ реагирует на сигналы прерывания, поступающие от датчиков прерывания, непосредственно связанных с объектом. Каждому сигналу прерывания соответствует переход ЭВМ к выполнению соответствующей программы, определяемой характером прерывания. Сигналы прерывания отрабатываются ЭВМ с учетом уровня приоритета.

При комбинированной связи ЭВМ с объектом управление осуществляется как по тактовым сигналам УТВ, так и по сигналам прерывания, например по сигналам аварийного режима объекта управления.

В ряде случаев целесообразно использовать прямое цифровое управление объектом на базе ЭВМ. В этих случаях ЭВМ выполняет функции регулятора контура управления. Датчик заданных значений величин, сложение задающих сигналов, сигналов обратных связей и регулятора реализуются в виде программных алгоритмов, а устройство сбора и регистрации переменных состояния и выдачи управляющих воздействий - в виде программируемого функционального устройства. На рис. 6.13, а представлена схема взаимодействия аппаратных и программных средств в системе прямого цифрового управления объектом.

На выходе объекта управления (ОУ), а следовательно, на входе вычислительной системы элементами системы сбора и регистрации информации осуществляется контроль переменных, характеризующих управляемый процесс. Результаты анализа состояния процесса (объекта) Ху с выхода устройства ввода данных управ-

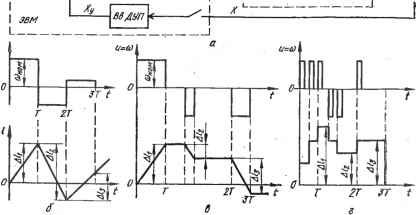Рис. 6.13. Взаимодействие аппаратных и программных средств в системе прямого цифрового управления:

- функциональная схема; б -управление с использованием амплитудно-импульсной модуляции; в - управление с использованием временно импульсной модуляции; г - управление с использованием числа импульсов

ляемого процесса (ВвДуп) поступают в точку смещения (ТС), где с учетом программ, генерируемых датчиком (ДПр), преобразуются в сигнал регулирования e\i), определяющий соответствующий алгоритм управления (АлУ) и выработку сигнала управления и на выходе устройства вывода данных управляемого процесса (ВДУП). Цифровые управляющие сигналы и передаются в соответствующие каналы контуров управления через мультиплексор (М) и заносятся в регистр ЭВМ.

ЭВМ выдает на каждый контур управления управляющее воздействие A fe = Uh-Wfe-i. При этом цифровые сигналы преобразуются в аналоговые для исполнительного органа и фиксируются в схеме задержки (СЗ). Функция задержки осуществляется для выдачи процессорных данных.

Между управляющим воздействием на объект управления y{t) и переменной е() имеет место следующая зависимость:

If de(t)

где k - коэффициент усиления; Ти - время изодрома; Тз - время задержки.

Величина y{t) определяет либо положение / выходного органа объекта управления, либо частоту вращения со выходного вала. В соответствии с этим реализуется либо алгоритм определения положения

(6.23)

либо алгоритм определения частоты вращения

На рис. 6.13, б показано изменение положения / в последовательные моменты времени опроса Т, 2Т, ... после того, как сформирован сигнал управления и = соном, где Т - промежуток времени между двумя соседними опросами.

На рис. 6.13, в для управления требуемым положением регулируемого органа использована импульсио-временная модуляция, а в случае, представленном на рис. 6.13, г, регулирование осуществляется генерированием определенного числа импульсов для пошаговой установки двигателя.

Алгоритмы прямого цифрового управления могут быть построены подобно алгоритмам аналогового регулирования, разработан-HbiN на основе заданной структуры системы и требуемых показа-тс.ей качества регулирования. При достаточно малом времени опроса ЭВМ, используя схему задержки (СЗ), может с достаточной точностью обеспечить моделирование соответствующего аналогового регулятора.

Рассмотрим формирование цифрового алгоритма управления на основе аналогового алгоритма (6.23). Непрерывные функции e(t) и y{t) при цифровом управлении определяются своими значениями впвп-и Уп, Уп-ъ ... только в моменты времени опроса кТ, k-l,n. На основании (6.23) в каждый момент времени управляющий сигнал

(1 бп -е„ 1 \ en--i:ekT + Ts---j (6.24)

Значение уп рассчитывается в каждый момент времени на основании значений Хп или c и предшествующих им значений Xn-i или

Алгоритмы прямого цифрового управления представляют собой дискретные аналоги дифференциальных уравнений аналогового регулирования. Интервал опроса состояния системы выбирается таким, чтобы цифровой регулятор был квазианалоговым. Квази-аналогоБЫЙ алгоритм часто имеет форму

т т

Уп = Ei ЬиУп-к + Сквп-к,

где fefe и Cfe - постоянные.

Прямое цифровое управление позволяет реализовать также алгоритмы, которые технически трудно преобразовать в аналоговую форму. Кроме того, цифровые регуляторы значительно расширяют типы возможных структур систем управления динамическими объектами.

На рис. 6.14 приведена система прямого цифрового управления электроприводом.

I I

с уапр УС

ЗУ

ОЗУ

свР

УВИ

Рис. 6.14. Система автоматического цифрового управления электроприводом

САУ используется для управления двухкоординатной системой воспроизведения движения, например, в периферийных устройствах вычислительных машин, в двухкоординатных станках с числовым программным управлением и т. п.

Объект управления (ОУ) представляет собой два малоинерционных электродвигателя - Дь Дг с полым якорем, подключенных на силовые преобразователи Cfli и СПг, которые выполнены как транзисторные импульсные усилители мощности. Двигатели оснащены датчиками положения (ДП), на выходе которых фиксируются значения управляемых переменных - координат х и у. Эти значения поступают на вход арифметического устройства (АУ), где обрабатываются вместе с выходными сигналами запоминающего устройства (ЗУ), оперативного запоминающего устройства (ОЗУ) и устройства формирования команд (УФК). На вход ЗУ поступают сигналы с выходов АУ, УФК и устройства ввода УВв. На вход УВв поступают сигналы с УФК и пульта управления (ПУ), а также автоматически вводимый сигнал правления (АВв). Устройство управления (УУ) получает сигналы САУ и передает их на устройство формирования команд (УФК) через совокупность элементов, включающих в себя синхронизатор (С), устройство выборки программ (УВПр) и устройство сравнения (УС).

Специализированное вычислительное устройство (СВУ) в целом осуществляет следующие функции: вырабатывает и преобразует управляющие воздействия; реализует выбранный закон управления; отрабатывает сигналы обратных связей по управляемым координатам. Эти функции выполняются с помощью устройств, входящих в СВУ. В арифметическом устройстве (АУ) осуществляются операции сложения, вычитания, умножения. Текущие координаты задающих сигналов, обратных связей и результаты промежуточных вычислений хранятся в ОЗУ, содержимое которого в течение отработки одного кадра многократно меняется. В ЗУ хранятся значения параметров объекта управления, информация о содержании текущего и следующего кадров, постоянные для отрабатываемого

кадра результаты промежуточных вычислений. УВ и ПУ обеспечивают ручной (РВв) и автоматический (АВв) ввод информации.

Устройство управления вырабатывает команды управления вводом, отработкой и выводом информации. Устройство вывода (УВИ) преобразует информацию, поступающую на его вход с АУ, в ши-ротно-импульсные управляющие сигналы бж и 6у, используемые для управления силовыми преобразователями СПь СПг- СВУ выполняется на интегральных микросхемах. В этом устройстве жестко заложены программы: 1) подготовка; 2) интерполяция; 3) расчет управляющих воздействий бж; 4) расчет управляющих воздействий 6у.

Программа ПОДГОТОВКА осуществляет установку исходного состояния, ввод следующего кадра и расчет коэффициентов закона управления координатами х п у. Программа реализуется один раз в начале каждого кадра.

Программа ИНТЕРПОЛЯЦИЯ управляет движением систем в режимах разгона, равномерного движения, торможения, ползучей ci.UjjoCTH. Программа реализуется после появления сигнала интерполяции и заканчивается с отработкой электроприводом координат конечной точки.

Программы РАСЧЕТ бх и РАСЧЕТ реализуются после появления сигналов X я у.

Прямое цифровое управление позволяет создавать системы автоматического управления с высокими динамическими показателями. Например, в рассмотренной схеме управления воспроизведением движения диапазон регулирования частоты вращения достигает ЫО, время отработки ступенчатых воздействий около 0,01 с, время перехода с максимальной частоты вращения до остановки с точностью до 1 мкм - около 0,1 с. Создание электромеханической системы автоматического управления с такими высокими показателями качества управления на основе традиционной элементной базы невозможно.

Сравнивая схему прямого цифрового управления с электромашинной системой управления частотой вращения, рассмотренной в гл. 1 (см. рис. 1.7), следует подчеркнуть отсутствие датчика частоты вращения - тахогенератора. Быстродействующее вычислительное устройство обеспечивает время вычисления управляющих воздействий в пределах интервала неуправляемости импульсного преобразователя.

Жесткая логика управления в схеме, приведенной на рис. 6.14, снижает возможности САУ, выполняемых по этому принципу. В частности, новые требования и задачи приводят к необходимости существенной перестройки или полной замены СВУ. Алгоритм управления должен разрабатываться на самом детальном уровне, вплоть до шагов, отражающих элементарные операции.

Существенно расширяются возможности управления в системах, функционирующих на базе микроЭВМ, с сохранением или даже со снижением стоимости программно-аппаратных средств. Здесь становится возможным использовать все преимущества микропрограммирования, позволяющего реализовать набор машинных ко-

<1>

ЦАП j г 11$мк1Т1роприбодам

звм

Рис. 6.15. Автоматизация многокоординатного управления динамической системой на базе микроЭВМ

манд стандартных ЭВМ, а также специальные наборы команд, эффективные для определенной области управления. Кроме того, можно реализовать конструкции языка программирования высокого уровня, ядро операционной системы реального времени, диагностические функции для быстрого обнаружения ошибок и сбоев. Возможность распараллеливания на микропрограммном уровне отдельных элементарных операций позволяет значительно повысить быстродействие исполнения алгоритмов.

В качестве примера на рис. 6.15 приведен аппаратный состав микропроцессорного управления многокоординатной динамической системой. В состав системы управления входит микроЭВМ с постоянным запоминаюш,им устройством (ПЗУ), устройством отображения - дисплеем (Д), системой ввода и вывода информации датчиков сигналов (ДС). Управляющая программа может вводиться с перфоленты (ПЛ), с клавиатуры дисплея или с пульта оператора (ПО). С помощью дисплея можно осуществлять коррекцию программы в памяти, задание системных параметров, расширенный диалог с системой.

Возможности системы в значительной степени определяются вйзможностями входного языка. Управляющая программа обеспечивает обработку контура, состоящего из отрезков прямых и дуг окружностей. Возможно управление вручную в режиме диалога с оператором.

Отметим особенности постоянного запоминающего устройства, использованного в схеме (рис. 6.15). ПЗУ - это память, позволяющая только прочитать то, что в ней записано, и не допускающая возможности хотя бы частичного изменения информации, занесенной в нее. Основное достоинство ПЗУ - неразрушаемость: хранимая в ПЗУ информация не разрушается при выключении питания. В ПЗУ хранятся неизменные программы: микропроцессор только считывает команды из ПЗУ и организует их выполнение, но не записывает новой информации в эту область памяти. Программа управления автоматической системой фиксируется в ПЗУ при условиях, не допускающих случайного или умышленного изменения информации, содержащейся в ПЗУ.

Примером эффективного входного языка систем рассматриваемого типа может служить язык КОНТР АН, разработанный в лаборатории электромеханических систем воспроизведения движения Новосибирского электротехнического института (НЭТИ). Язык

КОНТРАН предназначен для программирования обработки деталей на фрезерных пятикоординатных станках. Средства языка позволяют описать контуры, включающие отрезки и дуги окружностей, расположенных в различных плоскостях, задать контурные скорости для прохождения различных участков контура, обеспечить построение эквидистанты и выполнение ряда технологических функций.

Глава 7

МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ УПРАВЛЕНИЯ СЛОЖНЫМИ СИСТЕМАМИ

7.1. ОБЩАЯ ХАРАКТЕРИСТИКА. ОСНОВЫ МЕТОДА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Задачи управления сложными системами являются типичными оптимизационными задачами, которые описываются функциональными зависимостями (моделями), сложными с математической точки зрения, но простыми по структуре:

fo = fo{X,Y); (7.1)

и = fi {X,Y) (, =, 0, f =. 1, т. (7.2)

Здесь fo--полезность или значение критерия, характеризующего качество функционирования системы (всегда скаля:р); X - вектор переменных, которыми нужно управлять; Y - вектор переменных (и постоянных), не поддающихся управлению, но влияющих на fi. Соотношения (7.2) выражают тот факт, что управляемые переменные могут изменяться в определенных пределах. Уравнение (7.1), выражающее целевую функцию, совместно с ограничениями (7.2) образуют модель системы (задачи), которую необходимо решить.

Модель используют для отыскания точных или приближенных оптимальных значений управляемых переменных, т. е. таких значений, которые обеспечивают наилучший показатель качества функционирования системы при заданных значениях неуправляемых переменных. Как именно получается решение задачи, зависит от характера модели.

Модели могут быть линейными, если соотношения (7.1), (7.2) - линейные функции, и нелинейными, если эти функции нелинейные.-Для решения оптимизационных задач (7.1), (7.2) существуют различные методы. Независимо от метода, всегда находится оптимальное или близкое к нему решение. Оптимальным является решение, которое минимизирует или максимизирует (в зависимости от существа задачи) критерий качества (целевую функцию) на модели при заданных условиях и ограничениях, представленных в ней. При этом следует учитывать степень адекватности математической модели описываемой задаче. Вследствие того что модель никогда

точно не описывает задачу, полученное таким путем оптимальное решение никогда не является единственным наилучшим решением реальной задачи, а является аппроксимацией ее оптимального решения.

Если ограничения (7.2) представляют собой строчки равенства и в модель входит небольшое число управляемых переменных, то для отыскания решения часто можно использовать все классические методы математики, например дифференциальное исчисление или уравнения в конечных разностях. Если же эти методы оказываются неспособными привести к результату из-за отсутствия замкнутого аналитического выражения для /р вследствие сложности ограничений или большого числа переменных (большой размерности задачи), то прибегают к какому-либо итеративному методу математического программирования, являющемуся составной частью теории принятия решения - исследования операций. Сущность такого метода заключается в том, что вычислительный процесс начинают с некоторого пробного (допустимого) решения, а затем применяют алгоритм, обеспечивающий улучшение этого решения. Исходное пробное решение заменяют улучшенным решением, и процесс продолжают до тех пор, пока не станет ясно, что либо дальнейшее улучшение решения невозможно, либо стоимость дальнейших вычислений слишком высока. Ввиду громоздкости и большой размерности такие методы реализуют на ЭВМ.

В качестве метода решения оптимизационных задач используют линейное программирование (ЛП), представляющее собой раздел математического программирования, изучающий задачи нахождения экстремума линейных функций при линейных ограничениях в виде равенств или неравенств.

Линейное программирование - наиболее изученный и широко применяемый метод' исследования операций. Впервые идеи линейного программирования были изложены советским математиком Л. В. Канторовичем в 1939 г. в работе Математические методы организации и планирования производства .

В 1947 г. американский ученый Дж. Данциг опубликовал симплекс-метод решения оптимизационных задач, описываемых линейными моделями, а сам термин линейное программирование впервые появился в 1951 г.

Общая задача ЛП описывается математической моделью следующего вида:

максимизировать (минимизировать) линейную функцию

при ограничениях

fo{X)=±CiXi (7.3)

п

2] uijXj =: Gio, i = 1, -, П (7.4)

Z ацх^ < flio, t = г -f 1,I; (7.5)

2] 0 i = i + h ; in; (7.6)

Xj>0, /= (7.7)

T e. необходимо найти точку Х=(л:ь х„) п-мерного пространства, которая удовлетворяет системе ограничений (7.4) -(7.7) и максимизирует (минимизирует) целевую функцию (7.3). Иногда условие (7.7) отсутствует.

С организационно-экономической точки зрения модель (7.3) - (7.7) можно охарактеризовать так: есть возможность производить несколько видов продукции (/=1, п); для производства единицы продукции каждого вида (/) необходимо затратить различные ресурсы ац,1=\,т; количество имеющихся ресурсов каждого вида ограничено и равно am,i=\,tn; удельная прибыль от произведенной продукции или стоимость реализации ее равна Cj. Необходимо опредепить объемы (уровни) производимой продукции Xj, при которых оптимизируется (максимизируется или минимизируется) ре-),:.uii. производственной деятельности системы в целом без нарушения ограничений, накладываемых на использование ресурсов.

Линейные модели строятся при следующих допущениях:

1) пропорциональность - затраты ресурсов на производство вида продукции и вклад производственного продукта в целевую функцию прямо пропорциональны его уровню;

2) аддитивность - общая сумма ресурсов, расходуемых в системе при производстве всех видов продукции, равна сумме затрат ресурсов на отдельные виды продукции; общая прибыль (стоимость) складывается из частных прибылей (стоимостей), получаемых при реализации (производстве) каждого вида продукции;

3) неотрицательность - объемы произведенной продукции не могут характеризоваться отрицательными значениями.

Два первых допущения обеспечивают строгую линейность целевой функции (7.3) и ограничений (7.4) - (7.6).

Линейное программирование широко применяется при управлении сложными системами (отраслью промышленности, производственными процессами, запасами, транспортом, производственными предприятиями и т. п.).

При описании задач динамического характера коэффициенты модели (7.3) - (7.7) являются функциями некоторых параметров. Часто линейное программирование применяется для решения задач динамического характера, в которых результат предыдущего периода управления определяет исходную информацию последующего. Иногда линейное программирование используется для решения задач, содержащих информацию вероятностного характера. В этих случаях описание соответствующих случайных величин обычно сводят к эквивалентным детерминированным соотношениям.

Линейное программирование используется при решении задач статистики, при доказательстве основных теорем теории игр. Очень часто задачи, которые описываются нелинейными моделями, ап-

проксимируют линейными моделями и получают достаточно хорошие практические результаты.

Особым классом моделей линейного программирования являются транспортные модели, которыми описываются задачи выбора наиболее экономного плана перевозок сырья (продукта, изделий, товаров и др.) от т источников (производителей) к п пунктам назначения (потребителям).

Математическая модель такой задачи имеет вид: минимизировать

т п

fo{X) ICijXii (7.8)

i=i j=i

при ограничениях

Xij = at, t = l,m; (7.9)

T>Xii = bi, j l,n; (7.10)

Xij > 0, i = 1, m; / = 1, ft, (7-11)

где at--возможный объем поставок от t-ro источника; bj - спрос /-го потребителя; dj - стоимость перевозки единицы сырья t-ro источника к /-му потребителю; Xjj -объем перевозок от источника i к потребителю /.

Предполагается, что перевозимое сырье (продукт, изделия, товары и др.) одного вида.

В постановке задачи (7.8) -(7.11) требуется выполнение усло-

m п

вия 2] г = 2] bj, ЧТО всегда можно сделать, добавив фиктивный

г=1 j=l

источник или пункт потребления с тем, чтобы компенсировать .раз-

m п

НОСТЬ -

i=l j=l

Обобщением задачи (7.8) - (7.11) являются транспортная задача с промежуточными пунктами и транспортная задача с ограниченными пропускными способностями. Эти задачи удобно рассматривать на сети.

К задачам транспортного типа относятся:

задача календарного планирования производства, в которой для каждого из плановых периодов определяется оптимальный объем производства, удовлетворяющий плановый спрос;

задача о назначениях, в которой необходимо распределить т исполнителей по п видам работ. Эффективность использования каждого исполнителя на равных работах неодинакова.

Рассмотрим примеры построения моделей задач линейного программирования.

Пример 1. При производстве бетона для строительства используют четыре вида сырья: S s2, S3, S4; стоимость единицы каждого вида сырья соответственно Ci, Cj, Сз, С4. Бетон должен содержать компоненты трех видов. Количество компонента первого вида должно быть не менее Ь, елиниц, второго -единиц,