где A, B, C, D, E - постоянные коэффициенты.

В теории оптимального управления широко используются следующие математические методы: принцип максимума; динамического программирования; вариационного исчисления; математического программирования. Каждый из перечисленных методов имеет свои особенности и, следовательно, свою область применения.

Принцип максимума позволяет сравнительно легко учесть ограничения на управляющие воздействия, подводимые к объекту управления. Метод наиболее эффективен при синтезе систем, оптимальных по быстродействию. Однако реализация метода даже с использованием ЭВМ значительно затруднена.

Метод динамического программирования обладает большими возможностями. Однако для систем высокого порядка (выше четвертого) использование метода весьма затруднительно. При нескольких переменных управления реализация метода динамического Г(Г. раммирования на ЭВМ требует объемов памяти, превышающих возможности современных машин.

Вариационное исчисление применяется при отсутствии ограничений на переменные состояния и на переменные управления. Получение численного решения на базе методов вариационного исчисления затруднительно. Метод используется, как правило, для некоторых весьма простых случаев.

Методы математического программирования (линейного, нелинейного и др.) широко применяются для решения задач оптимального управления как в автоматических, так и в автоматизированных системах. Общая идея методов заключается в отыскании экстремума функции в пространстве многих переменных при ограничениях в виде системы равенств и неравенств. Методы позволяют найти численное решение широкого круга задач оптимального управления.

Достоинствами методов математического программирования является возможность сравнительно просто учитывать ограничения на управления и переменные состояния, а также обычно допустимые требования к объему памяти.

В настоящей главе рассматриваются принцип максимума и метод динамического программирования. Методы математического программирования рассматриваются в гл. 7, посвященной проблемам управления сложными - организационно-техническими и экономическими - системами.

5.3. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДИНАМИЧЕС1ШМИ СИСТЕМАМИ

Принцип максимума Понтрягина

Принцип максимума был сформулирован советским ученым Л. С. Понтрягиным в 1956 г. и доказан в ряде его последующих работ, созданных совместно с В. Г. Болтянским и Р. В. Гамкре-

лидзе. Этот принцип достаточно общий для определения условий существования оптимального управления щироким кругом систем.

Доказательство принципа максимума базируется на теории множеств, функциональном анализе и представляет определенные затруднения. Поэтому, не останавливаясь на доказательстве рассмотрим методику использования принципа максимума для синтеза оптимальных управлений.

Для использования принципа максимума уравнения объекта приводим к виду

dXi .

= Fi (хи Х2,.... Хп, щ, U2, ...,Цг), i= 1,п, (5.9)

где г - координаты управления,

или в векторной форме - F (X, U). Формулируем функционал качества управления

J = fF{X,U)dt, (5.10)

вычисляем функцию Гамильтона

H = tWi{t)Fi{X,U), (5.11)

где W{t) - вспомогательная функция, определяемая на базе уравнений Гамильтона

dxi дН дН (P¥i

Принцип максимума утверждает следующие условия оптимального управления: для осуществления оптимального управления необходимо существование таких ненулевых непрерывных функций Wi{t), чтобы функция Гамильтона Я как функция переменных управления достигла максимума. Вопрос о существовании функций Wi{t) рещается в каждом конкретном случае с учетом физического смысла процессов, протекающих в системе, и состава ее элементов.

Принцип максимума является методом рещения нелинейных задач оптимального управления, учитывающий ограничения на управляющие воздействия.

Рассмотрим использование принципа максимума для синтеза оптимальных управлений объектом, имеющим передаточную функцию Wo{p) х/и~1/р^, где X - выходная величина объекта управления; и - управление, прикладываемое к объекту.

Из выражения передаточной функции объекта имеем - = ~ и, ограничения [ы] < шах.

Введя обозначения х = хх; = 2, уравнения объекта приведем к виду (5.9)

dxi dx2

-dT ir = - (-i)

Ha основании (5.11) и (5.13) запишем функцию Гамильтона

Н = WiX2+W2U. (5.14)

Используя (5.12) и (5.14), найдем

dxi дН dx2 дН

~1Г ~d¥i dT д^

убедившись в соответствии уравнений Гамильтона функциям основных переменных.

На основании (5.12) и (5.14) получим

dT, дН d2 дН

Интегрируя (5.15), найдем вспомогательные переменные 4\=ci\ -fCidt-C2 - Cif, следовательно, на основании (5.14) имеем:

И = С1Х2+ (C2 - Cit)U = Ci--{- {C2 - Cit)U. (5.16)

в соответствии с принципом максимума оптимальное управление будет обеспечено, если (5.16) принимает максимальное положительное значение, т. е. второе слагаемое должно быть положительным и наибольшим. Это условие соблюдается, если управление обеспечивается по закону

и - Umax sign W2, т. е. ы = Umax sign (Сг - Cit). (5.17)

Оптимальная по быстродействию система управления обеспе-. чивает на фазовой плоскости Х2; Xi наиболее быстрый переход изображающей точки из произвольного начального состояния в на-

чало координат, где Xi = 0; = 0. Так как в (5.17) функция

Сг - Cit, являясь линейной функцией времени, может только один раз изменить свой знак, то указанный характер движения изображающей точки на фазовой плоскости возможен лишь при двух

значениях функции управления и: -f-Umax, - max.

В уравнениях (5.13) примем =1 и исключим время t, после чего получим dXi=X2dx2. Интегрируя, находим:

XI = х112 + с при ы = +1; (5.18)

XI = -ху2 4- с при ы = -1. (5.19)

Выражения (5.18) и (5.19) являются уравнениями фазовых траекторий рассматриваемой системы, оптимальной по быстродействию. При c=Q выражение (5.18) описывает параболу БОВь проходящую через начало координат, а (5.19) -параболу ЛОЛ1, также проходящую через начало координат (рис. 5.1). При сфО выражения (5.18) и (5.19) описывают множество парабол, сдвинутых вправо и влево от оси ординат. В синтезируемой оптимальной сис-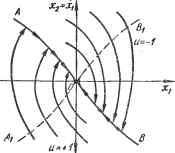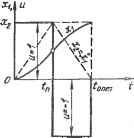

Рис. 5.1. Фазовый портрет системы, оптимальной по быстродействию:

<а - фазовые траектории; б - графики изменения фазовых координат и управляющего воздействия во времени

теме должны быть реализованы только те фазовые траектории, которые при управляющих воздействиях ы = ±1 обеспечивают быстрейщее движение изображающей точки к началу координат. При с=0 и и=\ этому условию отвечает траектория ВО, а при и= - 1-траектория ЛО. Следовательно, ЛОВ является линией, определяющей моменты переключения знака управления для обеспечения оптимального переходного процесса. Аналитическое выражение линии переключения можно получить из уравнений (5.18) и (5.19), приняв с=0:

(5.20)

Очевидно, что для осуществления управления, оптимального по быстродействию, необходимо обеспечивать изменение управляющего воздействия, прикладываемого к объекту управления, по закону

dx I dx \ dx

+1 при~< РИ

-1 при

для всех dx

\ dt h

>

для всех

(-)п>0-

При

\ dt /I

(5.21)

На рис. 5.1 вместе с фазовым портретом представлены графики изменения фазовых координат системы и изменения управляющего воздействия, обеспечивающего управление, оптимальное по быстродействию. Время переключения t-a можно определить из (5.17) в момент, когда ы=0: t-a-clcx.

Уравнения (5.21) выражают результаты аналитического конструирования регулятора системы, оптимальной по быстродействию, имеющей объект управления с передаточной функцией ]!fg(p) = l/p. Очевидно, что физическая реализация системы связана с необходимостью использования переключающего реле, обеспечивающего переключение с ы = -}-1 на и = -1 в момент вре-

jjeHH t = tn, и вычислительного устройства для вычисления и

/ dx \

сравнения этой величины с величиной ( ~L-

Метод динамического программирования (метод Беллмана)

Метод широко применяется для исследования оптимального управления как в динамических (технических), так и в экономически системах. Для реализации метода динамического программирования связи в системе между выходными переменными, управлениями и критериями оптимальности могут быть заданы как в виде аналитических зависимостей, так и в виде таблиц численных данных, экспериментальных графиков и т. п.

В основе метода динамического программирования лежит сформулированный Р. Беллманом принцип оптимальности . Для формулировки принципа Беллмана назовем управление, обеспечивающее оптимальное движение в системе, т. е. оптимальное управление u{t), решением. Принцип оптимальности Беллмана утверждает: оптимальное поведение системы характеризуется тем свойством, что каковы бы ни были первоначальное состояние и решения до некоторого момента вр1мени, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.

Принцип Беллмана вытекает из следующих рассуждений (рис. 5.2). Допустим, что в результате оптимального управления изображающая точка в фазовой плоскости переменных системы Х2, Xi движется по траектории аЬс из начального состояния л:(0) в конечное состояние х{Т). Допустим, что процесс движения начали рассматривать не с момента t=0, т. е. не с точки а, л:(0), а с некоторого момента t=ti, т. е. с точки Ь, x{ti). Очевидно, что дальнейшее управление будет оптимальным, если движение изображающей точки обеспе- чится по траектории bee, т. е. по той части траектории, которая была определена первоначальным решением, обеспечившим движение по траектории аЬес. Действительно, пусть, начиная с момента времени -= определена другая траектория, отличающаяся от траектории Ьес, О

SmxoL ?1занная на рис. 5.2. Рис. 5.2. Принцип оптималь-штриховои линией. Эта траектория обес- ности Беллмана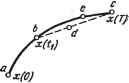

печивает меньшее значение функционала качества, выражающего потери на участке x{tx)-х{Т). Однако в таком случае окажется, что предыдущее решение, определившее оптимальную траекторию аЬес, было не оптимальным, что противоречит условию. .

Для использования метода динамического программирования уравнения объекта нужно привести к виду

- = f(x,u). (5.22)

Должен быть задан функционал, достигающий минимума при оптимальном управлении,

J = fF{x,u)dt (5.23)

и ограничения на управляемую и управляющую переменные: х^Х;

Весь интервал времени управления О- Т разобъем на N одинаковых промежутков

= TIN. (5.24)

Дифференциальное уравнение (5.22) заменим разностным уравнением

dx Ах Xi+1-Xi

= -= (-2)

где

Xi = X(lAt), i = l,N; Xi+i = Xi + Atf (xt, щ).

Переход от непрерывных функций (5.22) к разностным уравнениям влечет за собой замену функционала качества (5.23) приближенной суммой:

J AtF{Xi;Ui). (5.26)

Верхний предел суммы Л* - 1 объясняется тем, что площадь, выражаемая интегралом (5.23), заменяется суммой элементарных площадей с левой ординатой.

Рассмотрим процесс управления на последнем интервале времени, т. е. в интервале {N-\)M.t-NМ=Т.

Допустим, что значение управляемой переменной xn-\ в начале последнего интервала известно. Очевидно, что оптимальное управление на последнем интервале должно минимизировать функционал вида

/jv-i - AtF (xn-u un-i) , (5.27)

представляющий собой последний член в сумме (5.26). Следовательно, решение, т. е. закон оптимального управления на последнем этапе Un-i, обеспечивая /jv-i->min, должен удовлетворить заданным ограничениям.

Таким образом, найдено оптимальное управление на последнем участке как функция управляемой переменной Xn-i в н& интервала Un-i = (xn-i)

Рассуждая аналогично, для предпоследнего интер** (дг - 2)A<<(N-1)Д^ найдем оптимальное управление

UN-2 = 2 {Xn-2)

Приведенные рассуждения справедливы для всех интер^ , NMtO, т. е. {N-i)Att (N-i+l)М; u-i = (д^- Значения и^-г определяем после того, как составлены урав1< для всех интервалов Д^, включая первый, на котором x(0) заЯ^ Таким образом, сложная задача поиска оптимального ynpaBJ5 на всем времени управления заменяется более простой задаче* хождения оптимального управления на каждом шаге Д^.

В случае многомерной системы уравнение (5.22) и функц!* (5.23 становятся векторными, т. е. имеем:

= F{X,U); Х{ХиХ2,...х„}; U {щ, Uz,..., Ur};

J = fW(X, U)dt,

о

где п - число управляемых координат; г - число управлений-

Алгоритм вычисления оптимальных управлений в многомР^ системе аналогичен рассмотренному выше, но на каждом At должна осуществляться минимизация частичного функци(? Jn-1 по всем г переменным управления Ur.

Как видно из изложенного, численные значения управлй^** переменных x{t) и управлений u{t) по методу Беллмана по-У^ ются в дискретные моменты времени. Следовательно, точность Р^ шения зависит от того, насколько разностные уравнения эК лентны соответствующим непрерывным уравнениям. Для cf выше второго порядка замена дифференциальных уравнений Р^ ностными приводит, как правило, к приближенным решения задачи.

В задачах оптимального управления принцип оптималь* Беллмана выражается в виде нелинейного уравнения в ча производных первого порядка, полученного в результате при** ния метода динамического программирования к функции, вы ющей оптимальное значение функционала в зависимости о^ начального состояния. . ,

Пусть интервал управления О - Г не фиксирован, тогда / будет функцией Т. Если J{x, и) является непрерывной фун:* Всех переменных и всюду имеет непрерывные частные произвоД то в интервале t,t At имеем:

t+At

J [X (t) ,T]=mm{fF (x, u)dt + J [x (t+AT),T]}.

ua t

Разложив интеграл в ряд Тейлора по степеням Д^ в окрестности t и перейдя к пределу при Д^->-0, получим уравнение Беллма

S 260 129

dJ Г дПх, t) 1

-= min [F (X, u, t) + 2] --/1 (X, u, t) J (5.28)

Непосредственное нахождение оптимального управления на базе уравнения Беллмана весьма затруднительно и возможно лишь в ограниченных частных случаях. Тем не менее уравнение Беллмана позволяет обосновать некоторые варианты метода динамического программирования, обеспечивающие получение приближенных решений.

Обратимся к уравнению Беллмана (5.28). Если / в явном виде dJ

не зависит от t, то = 0. В задаче об управлении, оптимальном

по быстродействию, F{x,u)l.B результате уравнение Беллмана для систем, оптимальных по быстродействию, принимает вид

Т ri dJ Л

lien

ЪА. ЭКСТРЕМАЛЬНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ

Развитие техники управления потребовало создания таких автоматических систем, которые должны обладать свойством приспосабливания к изменениям внутренних и внешних условий функционирования. В таких системах параметры могут изменяться в широких пределах, причем сведения об этих изменениях обычно недостаточны для формирования управляющих воздействий на основании текущего измерения переменных состояния системы. Рассмотренные выше принципы управления (по отклонению, по возмущению, комбинированные) не только не обеспечивают требуемого качества управления, но в ряде случаев оказываются несостоятельными для создания работоспособной системы. В связи с этим во второй половине текущего столетия началась разработка и широкое внедрение адаптивных систем, способных приспосабливаться к изменениям внешних и внутренних условий (adaptio, лат.- приспособление). Адаптация в таких системах может рассматриваться как процесс накопления и использования информации в системе, направленный на достижение ее оптимального состояния при начальной неопределенности и изменяющихся условиях.

Адаптация применяется тогда, когда факторы, воздействующие на систему, полностью или частично неизвестны. В процессе адаптации система накапливает сведения об этих факторах и определяет их характеристики.

В настоящее время разработано множество типов адаптивных систем, среди которых широкое распространение в различных областях техники нашли экстремальные системы (ЭС) автоматического управления. Эти системы содержат объект с экстремальной статической характеристикой и оптимизатор - автоматическое устройство, обеспечивающее работу объекта в экстремальном ре-

жиме. При этом под экстремальным режимом понимается работа системы в районе экстремума статической характеристики.

В ЭС формируются такие управления на входе объекта (на выходе регулятора), которые обеспечивают экстремум функционала качества J = G(X, F, U), где X - вектор управляемых переменных; F - вектор возмущающих воздействий; U - вектор управлений.

ЭС наиболее эффективны в случаях, когда объект обладает статической характеристикой с достаточно ярко выраженным экстремумом, т. е. существует показатель качества управления, с изменением которого достигается существенное изменение технико-экономической эффективности. Техническая реализация принципа оптимального управления связана с необходимостью определения экстремума функционала качества и соответствующего воздействия на регулирующие органы объекта. Поэтому решение об использовании экстремального управления принимается после анализа его -ехнико-экономической эффективности с учетом дополнительных, иногда значительных затрат на обеспечение экстремального vn ..ления.

В настоящее время налажено промышленное изготовление оптимизаторов- типовых экстремальных регуляторов для использования в различных областях техники управления с целью существенного повышения технико-экономических показателей производственных и технологических процессов.

Примером ЭС может служить система регулирования температуры в газовых печах обжига строительных материалов (рис. 5.3, а). Интенсивность горения топлива и, следовательно, интенсивность нагрева X в печи определяется соотношением количеств подаваемого топлива q и воздуха и. На рис. 5.3, б показаны экстремальные статические характеристики объекта X=f{v) при различных расходах подаваемого топлива. Оптимальный режим работы определяется точкой А, лежащей на экстремуме характеристики Х= =f{v). Форма кривой X(v) и положение максимума зависят от многих факторов (возмущений) - расхода топлива, его калорийности, температуры подаваемого воздуха и ряда других. Задача ЭС в данном случае заключается в том, чтобы в любой обстановке в пределах заданных технических условий обеспечить оптимальный режим работы системы, т. е. режим, характеризуемый точкой А статической характеристики объекта X{v). Это обеспечивается соответствующим регулированием подачи воздуха при различных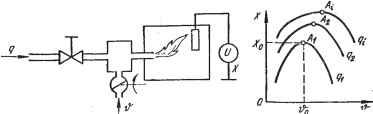

д 1 - 1У

Рис. 5.3. Система экстремального регулирования:

а - схема системы; б - статические характеристики объекта управления

! I I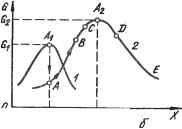

Рис. 5.4. Статические характеристики объектов экстремальных систем: а - с постоянным экстремумом; б - с изменяющимся экстремумом

условиях работы системы, определяемых указанными возмущениями.

В общем случае экстремальная автоматическая система управления должна выводить объект на экстремальный режим и удерживать его в нем. Сложность ЭС в значительной степени зависит от свойств объекта, выраженных в форме и положении его статических характеристик.

В наиболее простых случаях экстремальные характеристики объектов стабильны (фиксированы), и оптимальный режим достигается формированием управлений по отклонению управляемой величины от ее экстремального значения, а сами системы называются статическими экстремальными. ЭС подобного типа аналогичны рассмотренным ранее системам автоматической стабилизации регулируемой величины.

Более характерным типом ЭС являются динамические экстремальные системы, в которых статические характеристики объектов не фиксированы. Их положение может определиться как детерминированными факторами, так и случайными, причем второй тип систем является наиболее общим.

Для простоты рассуждений сначала остановимся на динамических ЭС с одномерным объектом и экстремальным показателем качества G{X, f), где X - регулируемая величина; f - возмущение. Рассмотрим два типа статических характеристик объекта - с экстремумом при фиксированном значении X (рис. 5.4, а) и с экстремумом, изменяющимся произвольно (рис. 5.4, б).

В первом случае уход объекта от оптимального режима сопровождается возникновением отклонения AX=Xq- X, где Хо - значение регулируемой величины в экстремальном режиме; X - текущее значение регулируемой величины. В этом случае ЭС строится как обычная система стабилизации регулируемой переменной с использованием принципа регулирования по отклонению.

Во втором случае задача обеспечения экстремального управления существенно усложняется, так как в зависимости от различных факторов экстремум характеристики G(X, f) смещается как по вертикали, так и по горизонтали. В таких случаях для осуществления экстремального управления необходимо автоматическое слежение за положением точки экстремума характеристики объекта.