В дальнейшем (п. 3.54) будет показано, что вихревые линии движутся вместе с жидкостью.

Если вихрь отличен от нуля, то говорят, что движение вихревое. Говорят также, что жидкость находится в состоянии безвихревого двиясения, если в каждой точке области, занятой движущейся жидкостью, вихрь равен нулю. В этой области жидкости не существует вихревых линий.

2.42. Циркуляция. Рассмотрим замкнутую кривую С, полностью расположенную в движущейся жидкости. Пусть q -вектор скорости в произвольной точке Р этой кривой, а Sj -единичный вектор касательной к кривой в точке Р (рис. 36). Направление касательной выбирается так, чтобы наблюдатель, движущийся из точки Р в направлении Si, описывал кривую в выбранном положительном направлении. Возьмем на кривой точку Q, близкую к точке Р, такую, что дуга PQ имеет бесконечно малую длину 6s. Мы можем тогда в точке Р образовать скалярное произведение qS6s = q6s, где бз -направленный элемент дуги в точке Р (ср. п. 2.20).

Образуя аналогичные произведения в точках Q, и т. д. вдоль всей кривой

снова до точки Р, мы определим циркуляцию вектора скорости вдоль замкнутой кривой С соотношением

Рис. 36.

Г = Ит 2q6s= \ qds-Циркуляция может быть записана в одной из следующих форм: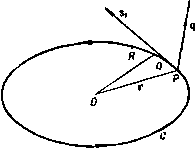

Г= Jqds= 5qdr= 5 qdP.

(С) (С) (С)

каждая из которых означает одно и то же.

Мы можем образовать циркуляцию любого вектора вдоль некоторой замкнутой кривой.

2.50. Теорема Стокса. Пусть 5 -поверхность, ограниченная кривой С*), а п -единичный вектор нормали к элементу площади dS, направленный в ту сторону, которая связана с направлением циркуляции вокруг dS и вдоль С правилом правого винта (рис. 37). Тогда имеет место равенство

J n(Vxq)dS= jj qds = r,

(S) (С)

которое выражает существо теоремы Стокса.

Доказательство. Если мы соединим точки кривой С семейством линий, лежащих на поверхности S так, чтобы образовать сетку, то мы увидим, что каждая ячейка сетки, за исключением тех, которые принадлежат кривой С, имеет линии, общие с соседними ячейками. Так как линии, которые принадлежат двум соседним ячейкам, проходятся дважды в противоположных направлениях, то, следовательно, циркуляция вдоль кривой С равна сумме циркуляции по всем ячейкам.

1) Такие поверхности можно условно представить как пленку, натянутую на контур С

Таким образом, достаточно доказать теорему для одной бесконечно малой ячейки сетки, покрывающей поверхность 5.

Так как любая ячейка может быть разделена на треугольники, то достаточно доказать теорему для одной треугольной ячейки ABC, стороны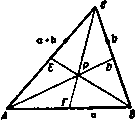

Рис. 37.

Рис. 38.

которой имеют бесконечно малую длину. Пусть D, Е н F -середины этих сторон (рис. 38) и пусть Я -центр тяжести треугольника; тогда можем записать

ЛВ = а; ВС=Ь; СЛ=-(а--Ь).

Обозначим через qm значение q в произвольной точке М. Тогда из определения интеграла следует приближенное равенство

J dsq=ABqF + BCtiD + CA<iB =

= а (QiT-Яе) + b (qo-Яв). Далее, из равенства (5) п. 2.31 следуют соотношения

qF = qp + ()qp; qB = qp + {PEV)qp. Вычитая одно из другого, получим равенство

- Яя = (EFV) qp = - Y (bV) Яр-

Аналогично

Следовательно,

Яс-Яя=(*) Ч^-

Jdsfl=-Ia(bV)-b(aV)Jflp =

= -1[(ахЬ)хУ]ф>-

Далее, ndS = V (axb), где dS-площадь треугольника ABC, и поэтому с той же степенью точности можем записать равенство

5 n(VXq)dS = l(aXb)(VXfl) = I(aXb)xVlflp.

Сравнивая последнее равенство с равенством (3), легко установить спра ведливость теоремы Стокса для бесконечно малого треугольника и, следовательно, для произвольной поверхности, которая может рассматриваться как предел суммы бесконечно малых треугольников. Граничная кривая

ЭТОЙ поверхности может рассматриваться как предел границы вписанных многоугольников.

Теорема Стокса, сформулированная выше, является частным случаем более общей теоремы, которую можно сформулировать следующим образом, если использовать понятие направленной площади:

(S) (С)

где X -произвольная скалярная или векторная функция координат, а ds - направленный элемент дуги кривой С (рис. 39).

Доказательство. Как и в предыдущем случае, достаточно доказать эту теорему для отдельной ячейки сетки. Точно таким же образом, как и при доказательстве предыдущей теоремы, можно получить соотношение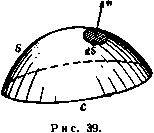

UsX=-la[bi]X--b

1(ахЬ)Х^]л,

а так как величина /< а х b представляет собой направленную площадь треугольной ячейки, то утверждение теоремы доказано для одной ячейки сетки и, следовательно, для общего случая.

В еще более общей форме теорему можно записать следующим образом:

[(Sx)x] = j4(dsX).

Доказательство теоремы в этой формулировке проводится точно так же, как и вышеприведенные доказательства. Необходимо отметить, что первые символы д/дР с каждой стороны равенства (4) мы можем заменить той же самой операцией, повторенной п раз.

2.51. Следствия из теоремы Стокса. Подставляя в формулы п. 2.50

вместо символа X выражения q, ф, xq, мы получим следующие соотношения:

5 qds= 5 (nxV)qdS= J n(Vxq)dS =

(8) <S)

gdS,

= 5ngds= 51

(S) (8)

где С-вектор вихря. Таким образом, циркуляция скорости по любому замкнутому контуру равна интегралу от нормальной компоненты вектора вихря по любой поверхности, натянутой на этот контур*):

J фй8- J (nxV)фdS, (2)

(С) (8)

Jd8Xq= J(nxV)XqdS=- [ n(Vq)dS-f J (V;q)ndS. (3)

<C) (8) (g) (S)

) To есть равна потоку вектора вихря через любую поверхность, натянутую на кон-гур.- Прим. ред.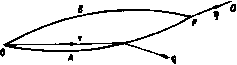

J qd8= J qd8=-фр. (1)

P и с . 40.

(ОАР) (ОВР)

Здесь фр -скалярная функция, величина которой зависит только от положения точки Р (и положения фиксированной точки О) и не зависит от выбора пути из точки О в точку Р. Далее, выберем точку Q настолько близкой к точке Р, что можно считать вектор скорости q постоянным вдоль отрезка PQ.

Обозначим через i\ радиус-вектор точки Q относительно точки Р. Тогда можно записать следующее приближенное соотношение:

- Л?Ф= - Фд--фр= J qds=:qi), (PQ)

где через ф обозначено фр.

Так как Q -произвольная точка, близкая к точке Р, то вектор ij также произвольный и, следовательно,

q=-Vф. (2)

Таким образом, если движение жидкости безвихревое, то вектор скорости является градиентом некоторой скалярной функции') координат -ф.

Эта скалярная функция называется потенциалом скорости. Мы доказали необходимость существования потенциала скорости при безвихревом движении жидкости. Обратно, если существует потенциал скорости, то движение жидкости является безвихревым, так как, согласно формуле (3) п. 2.32,

VXq = - VX (Уф) = 0.

Кроме того, из свойств векторной функции ?ф следует, что скорость жидкости в любой точке перпендикулярна поверхности ф = const, проходящей через эту точку. Другими словами, линии тока ортогональны эквипотенциальным поверхностям.

2.53. Консервативное поле сил. Рассмотрим консервативное поле сил (см. п. 1.42). Работа, совершенная силой поля F при перемещении единичной массы из точки О в точку Р, не зависит от пути. Таким образом

1) Значение этого термина см. в п. 3.70.

2) Одни авторы берут эту функцию со знаком минус, а другие-со знаком плюс. Взяв знак минус, мы следуем Ламбу. В этом случае равно импульсивному давлению, которое вызывает движение в покоящейся жидкости (ср. п. 3.64).

2.52. Безвихревое движение. Пусть О-фиксированная, а Р -произвольная точки некоторой односвязной области, в которой движение жидкости является безвихревым. 0>единим точки О Р двумя кривыми ОАР и ОВР, каждая из которых лежит в нашей области (рис. 40).

Тогда для замкнутой кривой ОАРВО, согласно теореме Стокса, имеет место соотношение

J qds+ \ qds= J n(Vxq)dS,

(GAP) (PBO) (S)

где S-произвольная поверхность, натянутая на контур ОАРВО и целиком лежащая в рассматриваемой области. Так как движение безвихревое, то

V X q = О и, следовательно.

Векторы 59

(см. рис. 40), можно записать соотношение

J Fdr= J Fdr=-Qp,

(oap) (овр)

где Qp -скалярная функция, величина которой зависит лишь от координат точки Р (и координат фиксированной точки О).

Формально это уравнение не отличается от уравнения (1) предыдущего пункта, и поэтому, проведя те же рассуждения, мы можем получить равенство

F= -Vfl.

где й-скалярная функция, называемая силовым потенциалом. Физически величина Q равна потенциальной энергии поля, т. е. энергии, преобретаемой единицей массы при перемещении от точки О к точке Р.

В дальнейшем знак минус в формуле (2) п. 2.52 обеспечит математическую (но не физическую) аналогию между потенциалом скорости и силовым потенциалом.

2.60. Теорема Гаусса. Рассмотрим замкнутую поверхность S, ограничивающую объем V. Пусть X -скалярная или векторная функция, зависящая от координат точки в пространстве. Тогда, если обозначить элемент объема V через dx, а элемент поверхности S -через dS, то можно записать следующее равенство, которое выражает теорему Гаусса*):

J (VX)dT=-J nXdS,

(V) (S)

где n -единичный вектор внутренней нормали к элементу поверхности dS.

Доказательство. Разобьем объем V на элементарные объемы тремя семействами параллельных плоскостей. Если бт-один из таких элементарных объемов, то мы можем записать приближенное равенство [см. формулу (1) п. 2.24J

(?Х)бтх= - 5 nXdS. (>

Этот интеграл берется по поверхности 6S объема бт. Просуммировав последнее равенство по всем элементарным объемам, получим соотношение

\ (VX)dT = lim2:(VX)6T=-2: \ nXdS.

Далее, в произвольной точке общей границы двух соседних элементов внутренние нормали к каждому элементу имеют противоположные знаки. Следовательно, поверхностные интегралы по границам, разделяющим соседние элементы объема, взаимно уничтожаются н остается только интеграл по поверхности S, что и требовалось доказать.

Заметим, что в последней теореме знак минус появился вследствие того, что мы использовали внутреннюю нормаль к элементам замкнутой поверхности S (рис. 41). Таким образом, в приложениях этой теоремы к гидродинамике мы будем применять нормаль, направленную внутрь жидкости, если S будет граничной поверхностью.

>) Gauss С. F., Theoria attractionis. Comm. soc. req. Gott., v. П. Gottingen. 1813. B отечественной литературе эту теорему обычно называют теоремой Гаусса-Остро-тршлаюто.-Прим. ред.]

Следует упомянуть, что строгое доказательство теорем Стокса и Гаусса и различных следствий, выводимых из этих теорем, основывается на некоторых предположениях о существовании и непрерывности частных производных, которые появляются при формулировке теоремы.

Разрывность параметров движения жидкости проявляется физически, если движение жидкости разрывное, и поэтому мы не будем рассматривать условия, при которых справедливы сформулированные теоремы, так как

это увело бы нас слишком далеко от главной темы.

Если область, ограниченная поверхностью S, является т-связной областью (см. п. 3.70), мы превратим ее в односвязную, проведя т- 1 перегородок В Вг, Bm-i. и будем рассматривать каждую сторону перегородки как отдельную границу. Таким образом, в случае двусвязной области мы получим единственную перегородку В, стороны которой обозначим В* (положительная сторона) и В' (отрицательная сторона). Тогда из теоремы Гаусса, примененной к полученной таким образом односвязной области, следует равенство

5 VXdx=- nXdS- 5 nXdS- пХdS.

Рис. 41.

Для любой точки в поверхности справедливо равенство п*4-п = 0. Введем обозначение скачка функции X при пересечении перегородки В с отрицательной стороны на положительную следующим образом:

х*-х-~\х\.

Тогда теорема Гаусса для рассматриваемой двусвязной области запишется в виде

(V) (S) (В.)

Если m > 2, то мы просто добавим в правой части последней формулы члены для других перегородок.

2.61. Следствия из теоремы Гаусса. Пусть а -некоторый вектор, а ф - некоторый скаляр. Заменим в теореме Гаусса выражение (VX) последовательно на Va, Vxa, Уф, ()Ф, (VV)a, V(q; а).

Тогда мы получим следующие равенства:

5VadT=

<V)

V X а dt =

?ф dt :

- \ nadS,

т = -

nx adS,

J Пф dS,

\ (nV)фdS= - \ -dS, (CM. П. 2.22),

<S) (S)

(2) (3) (4)

HiadSj- n2ad52= VadT = 0,

(S,) (Si) (V)

так как, по определению'), Га = 0 и так как на боковой поверхности векторной трубки nadS = 0.

Таким образом, величина Л= nad5 остается постоянной вдоль векторной трубки. Мы назовем величину А интенсивностью векторной трубки. Следовательно, мы можем определить единичную трубку как трубку единичной интенсивности и говорить о числе единичных трубок N, которые охватывает данный контур С.

2.62. Теорема Грина ). Из (}юрмулы (VI) п. 2.34 для произвольного вектора а можно получить равенство

V (фа) = а (Уф) + ф (Va).

Таким образом, из соотношения (1) п. 2.61 мы получаем равенство

- naфdS= a{V<f)dx+ ф(Va)dт.

(S) (V) (V)

) См. примочанне на стр. 48.

Green G., Essay on Electricity and Magnetism, Nottingham, 1828.

f V2adt= - J {nV)adS, (5)

(V) (8)

jj V(q;a)dT= - n(q; a)dS. (6)

(V) (S)

Последнее равенство может быть названо тензорной формой теоремы Гаусса.

Используя формулу (X) п. 2.34, это равенство можно свести к следующему виду:

а (nq) dS = - [а (Vq) + (qV) а] dr. (7)

(S) (V)

Теорема Гаусса может быть сформулирована также сл едующим образом

\dV=-\dSX. (8)

(V) (S)

Здесь через dV обозначен элемент объема, а через dS -вектор элемента площади поверхности, направленный внутрь объема, ограниченного этой поверхностью.

2.615. О)леноидальный вектор образует трубки постоянной интенсивности. Если векторная функция а задает некоторое векторное поле, то векторными линиями поля называются линии, касательные к которым в каждой точке направлены вдоль вектора а, проведенного в этой точке (ср. линии тока). Векторная трубка образуется векторными линиями поля, проведенными через каждую точку некоторой замкнутой кривой. Рассмотрим часть векторной трубки, заключенную между двумя плоскими сечениями 5, и Sj, внешние нормали к которым обозначим через п, и - п.. Из теоремы Гаусса можно получить равенство

ffi Глава 2

Подставляя сюда вместо вектора а вектор Щ, где -некоторая скаля>-ная функция, и замечая, что n(Vi))=- (см. п. 2.22), мы приходим к следующему соотношению:

J (W)dT= - J q)V i,dT- С q)-dS= - С V <pdT- J t 5-dS. (1)

(V) (V) (g) CO (S)

Второе равенство следует из того, что выражение в левой части не изменится, если скаляры ф и if поменять местами. Равенство (1) представляет собой содержание теоремы Грина, или первое тождество Гршю.

Непосредственным следствием теоремы Грина является второе тождество Г рина

j(9V i,-*V4)dT= - j (-ys. (2)

Положим в равенстве (1) tp - . Тогда

[ (Уф) (Уф) Л = - J фУф dx- 5 ф Л5. (3)

(V) (V) (S)

Определение. Любое решение ф уравнения Лапласа

называется гармонической функцией.

Если ф-гармоническая функция, то из формулы (1) следует равенство

J(Vv)(V)dT=-5-g-dS. (4)

(V) <8)

Положим в этом равенстве =1. Тогда

-dS = 0. (5)

Если ф и - гармонические функции, то из формулы (2) получаем равенство

j (ft-*-) ->- <в>

В теореме Грина функции ф и должны быть однозначными, т. е. каждой точке Р области V должно соответствовать только одно значение функции ф и одно значение функции . В наших приложениях эти функции обычно будут выражать потенциалы скорости, и требуемое условие будет выполнено, если область течения односвязна'). Если же функции Ф и 1> являются потенциалами скоростей в многосвязной области течения, то условие однозначности может быть нарушено вследствие существования циркуляции. При наличии циркуляции формулировка теоремы Грина должна быть изменена.

Предположим, например, что область двусвязна и что на перегородке В, которая делает область односвязной, существует постоянный скачок функций ф и tj;, равный соответственно х и Я. Эти величины называются цик-

i) См. п. 3.70.

шческими постоянными перегородки. Следовательно, имеют место следующие равенства:

Ф* ф- = [ф]-х: Г-Г = № = - (7)

Тогда из предыдущих рассуждений следуют равенства

(v) (V) (S) (в.)

5фУ Ф^т-$Ф^5-х 5d5 =

(v) (s) (в*)

- \ V\dr- 5 *5-dS-?. [ .dS. (8)

(V) (S) (Й*)

Крайнее правое равенство получено с использованием формулы (4), где ф заменено на ф. Эта замена законна, так как при этом выражение в левой части не изменяется.

Формула (8) выражает содержание теоремы Грина для двусвязной области. Для л-связной области в правую часть формулы (8) следует добавить интегралы по всем остальным перегородкам. Например, если п = 3, то формула примет следующий вид:

5w*)dT=- vVdt-jvdS-x. [ dS-x, j dS.

(v) (v) (S) (bj) iBi)

2.63. Приложения теоремы Грина. Возьмем замкнутую поверхность S, охватывающую область, в каждой точке которой справедливы равенства

7 Ф = 0, 7 ф = 0.

Тогда из теоремы Грина следует соотношение

Возьмем точку Р, внутреннюю по отношению к поверхности S, и обозначим через г расстояние от точки Р до элемента поверхности dS. Мы докажем, что если фр-значение функции ф в точке Р, то справедливо равенство

. )та формула определяет значение функции в произвольной точке внутри области через значения этой функции на границе области.

Доказательство. Возьмем ф = 1 /г. Легко доказать равенство V* (1 г) 0. Окружим точку Р сферой 2 с центром в этой точке. Радиус сферы R мал, так что сфера 2 целиком лежит внутри поверхности S. Применим формулу (2) п. 2.62 к области, заключенной между поверхностями 1 и Так как на поверхности 2 имеет место равенство dn = d/?, то получаем соотношение

(V) (S) (S)

Так как первые два интеграла не зависят от величины R, то не должен зависеть от и третий интеграл, который равен, следовательно, своему предельному значению при R-*0 (рис. 42). Если выбрать R настолько малым, что на всей сфере ф = фр с точностью до малых второго порядка, то предел этого интеграла можно вычислить следующим образом: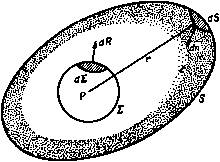

4я/?*= - 4яфр.

Отсюда мы получаем третье тождество Грина

Рис. 42.

(v) (8)

Так как ?*ф = 0, то это равенство и доказывает формулу (2).

Из равенства (1), кроме того, следует, что если точка Р лежит вне поверхности S, то левая часть равенства (2) обращается в нуль.

2.70. Декартовы координаты. Если выбраны три взаимно перпендикулярные оси Ох, Оу, Ог и три единичных вектора i, j, к, параллельные этим осям, то любой вектор а может быть выражен через свои компоненты) а^, йу, Ог. вдоль осей координат в виде

а = аЛ-с„Ц-а^к.

Так как векторы I, j, к взаимно перпендикулярны, то их скалярные произведения выражаются равенствами

i = j =k =l, ij = jk = kl = 0,

а векторные произведения этих векторов -равенствами

lxl = jxj = kxk = 0; jxk = l; kxl = j; ixj = k.

Взяв второй вектор b, мы получим для скалярного произведения векторов а и b выражение

ab = (Icx -Ь\а„ -f- кс,) (16, + \Ьу -Ь к6,) = с,6, + а„6 -\- а^Ь^.

Векторное произведение этих векторов записывается в виде

а X b = (la, -Ь \а„ + кс,) х (ife, + jb + kfe,) = = ia,X(i6x + j6 + k6,)-f

-Ь jay X (ifex + j6 + к6,) -4- ka, x (i6:c + jfey + kfe,) = = I {ayb - aby) + j (a,6x -Oxz) + к iflby - Uyb).

Векторное произведение можно записать более удобно в виде опреде-

к

1) Это обозначение для компонент вектора очень удобно. В соответствии с ним компоненты вектора скорости q обозначались бы Qx, Qy, Qi, хотя чаще их обозначают и, v, w. Мы будем использовать оба обозначения для компонент вектора q.