причем здесь для случая воздуха было принято р = 2,5. Соответствующая линия тока в плоскости годографа представляется кривой

2Р+1 sine

(12)

которая проходит через точки возврата огибающей, причем т здесь определяется формулой (8), а cos29 = -1/2р.

Эта линия тока изображена на рис. 342 жирной линией. Она касается огибающей в точках возврата и проходит в область за этой огибающей. Область справа от этой линии тока является запретной областью, в которой течение физически невозможно. Чтобы получить сопло, можно взять в качестве его твердых стенок любые две линии тока, расположенные левее указанной критической линии тока.

Отметим также, что окружность постоянной скорости, на которой д = с*, определяется значением т=1/(2р + 1). Тогда течение в части сопла, соответствующей области внутри этой окружности (заштрихованная область на рис. 342), является сверхзвуковым. Таким образом, течение Ринглеба, помимо того, что описывающее его решение точно удовлетворяет уравнениям в плоскости годографа, представляет собой еще и пример течения сжимаемого газа, в котором переход от дозвукового режима к сверхзвуковому и обратно происходит без скачка.

Из формулы (12) следует также, что максимальное значение скорости, которое достигается на критической линии тока, имеет место при 9 = п/2 и равно

8g 5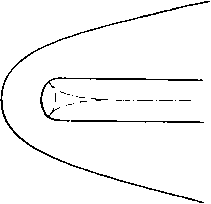

Рис. 343.

jj2- = -9- (для воздуха).

Следовательно, максимальное значение местного числа Маха, которое достигается в течении Ринглеба, равно

= ( ?EI iii Y=2,5 (для воздуха).

Аналогичное исследование можно провести и для решения (3) п. 20.32.

Оказывается, что здесь кривые постоянной скорости представляют собой трохоиды, которые имеют огибающую с двумя точками возврата. Критическая линия тока проходит через точки возврата и разделяет течение на две области, в одной из которых течение физически невозможно, а в другой, напротив, возможно (рис. 343). В этом случае течение из дозвукового переходит в сверхзвуковое и затем обратно без скачка. Максимальное число Маха для воздуха достигает здесь значения, примерно равного 2.

Сравнивая рисунки, приведенные в этом пункте, с рис. 341, видим, что в несжимаемом случае запретная область течения вырождается в прямую линию.

20.40. Движущееся возмущение. Прежде чем обратиться к сверхзвуковому течению, рассмотрим одну специальную задачу. Пусть в неподвижном воздухе в некоторой точке Р возникает слабое мгновенное возмущение, такое, KiK. например, резкий звук.

Такое возмущение будет распространяться в виде сферической волны, центр которой находится в точке Р и которая движется со скоростью звука с. Следовательно, в момент времени t, 2t, 3<, . . . возмущение достигнет точек, которые лежат на концентрических сферах радиусов ct, 2ct, Set, ... с центром в точке Р (рис. 344). Но если воздух не покоится, а движется слева направо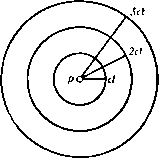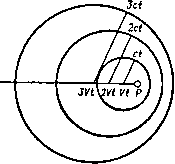

Рис. 344.

Рис. 345.

СО скоростью V, то точки, которых возмущение достигает в моменты времени nt, будут лежать на сферах радиусов net с центрами, расположенными на расстояниях Vnt от точки Р. Если У < с, то эти сферы не будут пересекать друг друга, и, как это показано на рис. 345, в этом случае возмущение достигнет

в конце концов любой наперед заданной точки пространства.

Однако если У > с, то картина будет иной (рис. 346), так как в этом случае возмущения никогда не достигнут точек, лежащих вне конуса, у которого вершина находится в точке Р, ось направлена по скорости V, а угол раствора равен 2]i, где sin (i = с/У = 1 /М, Угол ц называется углом Маха, а соответствующий конус - конусом Маха.

В плоском движении конус Маха переходит в клин, а линии, по которым этот клин пересекает плоскость движения, называются линиями Маха.

Аналогичное явление наблюдается и тогда, когда равномерный поток со скоростью V > стечет параллельно стенке (рис. 347), которая является гладкой всюду, за исключением одной точки Р, где имеется небольшая неровность (такая, например, как выступающий шов). В точке Р возникает возмущение, которое непрерывно поддерживается набегающим потоком, когда он достигает точки Р. Волны, непрерывно возникающие в точке Р, создают заметное возмущение только там, где они расположены наиболее концентрированно, т. е. на линии Маха т, исходящей из точки Р. В установившемся движении возмущение в любой точке на линии Маха т будет одинаковым; при перемещении от стенки вдбль линии m возмущение не затухает (по крайней мере теоретически). Если на стенке имеется несколько таких небольших неровностей, то каждая из них будет вызывать свою линию Маха. Вдоль такой линии плотность воздуха несколько отличается от плотности невозмущенного.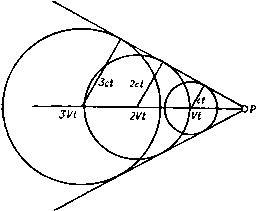

Рис. 346.

течения, и это обстоятельство делает возможным фотографирование линий Маха, существование которых, таким образом, хорошо подтверждается.

Из сказанного выше ясно, что сверхзвуковое течение, в котором скорость воздуха превосходит критическое значение, отличается физически от дозвуко-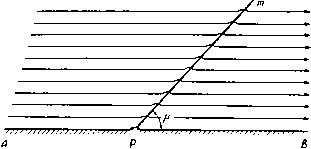

р и с. 347.

вого течения. Математически это проявляется в том, что дифференциальные уравнения меняют свой тип, переходя из эллиптических в гиперболические.

20.41. Характеристики. Рассмотрим геометрическую поверхность С, которая предполагается движущейся в газе. Пусть точка Р, принадлежащая этой поверхности, имеет скорость Цс и пусть q представляет собой скорость той частицы газа, с которой точка Р совпадает в данный момент. Тогда скорость точки Р этой поверхности относительно газа будет равна (qc - q).

Определение. Характеристикой называется поверхность, которая движется в газе таким образом, что в каждой точке Р этой поверхности величина составляющей скорости относительно газа в направлении нормали к этой поверхности равна местной скорости звука.

Следовательно, в символической форме

n(qc-q) = ±с,

где с - скорость звука в точке Р, а п - единичная нормаль к характеристической поверхности в точке Р.

Поскольку малые возмущения распространяются со скоростью звука (см. п. 14.86), то отсюда следует, что фронт волны, вызванной малым возмущением, является характеристикой i).

20.42. Характеристики в установившемся движении. В случае плоского установившегося движения, которое мы здесь только и будем рассматривать характеристики представляют собой неподвижные цилиндрические поверхности, которые пересекают плоскость движения по некоторой кривой. Таким образом,

nq = ±c или qn=±c, (1)

где q - нормальная составляющая скорости газа.

Итак, если линия РГ, (рис. 348) представляет собой касательную к характеристике Ci и если PQ - есть вектор скорости газа в точке Р, то проекция PQ на нормаль в этой точке Р будет равна скорости звука с. Далее, если р -

) Levi-Civita Т., Caratteristiclie е propagazione ondosa, Bologna, 1931. *) Теорию характеристик можно применять также в осесимметрнчных установившихся движениях. Для простоты изложения здесь мы рассматриваем только плоский случай.

острый угол между касательной к характеристике и вектором скорости, то

sin 11 = -= я

Угол fl называется углом Маха (см. п. 20.40).

Из формулы (2) ясно, что угол Маха может существовать только для числа Маха М> 1. Следовательно, действительные характеристики в смысле

О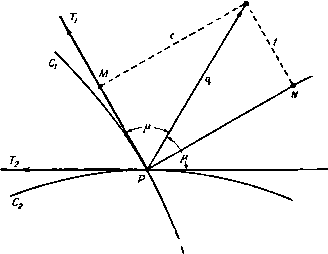

Рис. 348.

данного выше определения существуют только там, где течение является сверхзвуковым. Из рис. 348 и формулы (2) следует также, что имеются два возможных направления касательной к характеристике в точке Р, а именно PTi и Т'гР, каждое из которых образует угол (i с направлением скорости PQ.

Таким образом, в сверхзвуковом течении газа через каждую точку проходят две характеристики.

Направление характеристик можно просто найти с помощью адиабатного эллипса (рис. 349), уравнение которого в плоскости годографа в декартовых координатах и, V имеет вид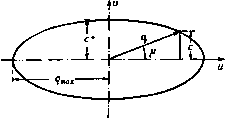

Рис. 349.

i7max

Чтобы с помощью этого эллипса ) определить направление касательных

к характеристикам в точке Р, проведем из точки Р вектор скорости PQ = q и расположим эллипс так, чтобы центр его находился в точке Р, а сам он проходил через точку Q. При этом возможны два положения эллипса, в каждом из которых большая ось эллипса будет направлена вдоль касательной к соответствующей характеристике в точке Р.

Что касается знака направления касательных к характеристикам, то можно условиться принимать за положительное направление нормали такое

1) В соответствии с п. 1.63, с*/(7ща1= У^{у-U/(Y+1). поэтому для различных значений Y все адиабатные эллипсы подобны.

направление, которое образует острый угол с вектором скорости, а за положительное направление касательных РГ и РТг принимать такое направление, которое получается поворотом нормали на прямой угол против часовой стрелки. В таком случае касательная PTi на рис. 350 составляет угол fl с вектором q, а касательная РГг -угол я -(i.

Оютветствующие касательные составляющие скорости имеют вид q cos \i = t w. - <7 cos л = - t.

Нормальные составляющие скорости по определению в обоих случаях равны с, и поэтому уравнение Бернулли (4) п. 1.63 дает

= (9S.ax - <?cos fl) = {qUx - n (3) * Yzii (4)

Линии Маха, рассмотренные в п. 20.40, аналогичны характеристикам, изученным

в этом пункте. Для установивщегося движения термины линия Маха и характеристика по существу равнозначны.

20.43. Изменение скорости вдоль характеристики. Для установившегося плоского течения уравнение неразрывности (3) п. 19.82 имеет вид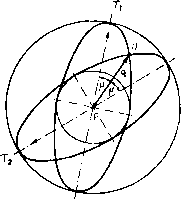

Рис. 350.

+X Q, = 0,

где ds -элемент дуги линии тока, х„ = 59/5п -кривизна ортогональной траектории к этому элементу. Здесь Э -угол, который касательная к линии тока составляет с некоторым произвольно выбранным направлением.

Если, кроме того, течение является безвихревым, то g = 0, и поэтому, согласно уравнению (4) п. 19.82, получим

где x, = (39/5s -кривизна линии тока. Предположим теперь, что течение является гомэнергетическим. Тогда по уравнению Крокко из п. 20.01 следует, что это течение является также изэнтропическим. Таким образом, формула (3) п. 1.61

qdq=-=-c

будет иметь место не только для линии тока, но и для любого другого направления.

Из уравнений (1) и (3) последовательно получим

Q ds

дд I дд ds с ds

Рассмотрим теперь изменение скорости q при перемещении по характеристике от точки Р до некоторой соседней точки R. Пусть касательная PTi к характеристике образует острый угол ц с касательной PS (рис. 351)

К ЛИНИИ тока, проходящей через точку Р. Из формул (2) и (4) имеем

Но, как видно из рис. 351, dn = dstgn и поэтому dg=qigVi(§dn + §ds)=qtgVide.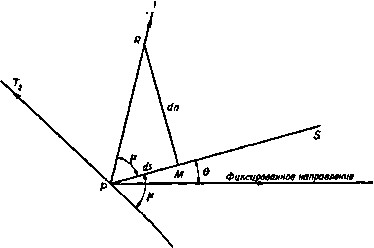

Рис. 351.

Т. е. вдоль PTi имеем равенство

Для другой характеристики, проходящей через точку Р, при замене р. на я -А вдоль PTi выполняется равенство

= -ctgn.

20.44. Характеристические координаты. Рассмотрим характеристику, касательная PTi к которой образует в точке Р угол ц с вектором скорости. Если / - составляющая скорости q вдоль PTi, то t = qcQS,yi, и поэтому с помощью равенства (5) п. 20.43 получим

dt = cos i d(7 - <7 sin А di = (7 sin ц (dO - dA), Используя формулу (3) п. 20.42 и замечая, что (7 sin ц = с, находим

dO -du= - = - ,

<?тах 2

6 -i= -arcsin;r--4 +О'

где (а - я - произвольная постоянная интегрирования. Для критической скорости звука q=c* получаем А = уЯ, и, следовательно, 8= о.

) Т е m р 1 е G., The method of characteristics in supersonic flow, R. and M., Ns 2091 (1944). Излагаемое нами описание метода характеристик, первоначально развитого Бузема-ном, основано на этой статье Темпла.

С ПОМОЩЬЮ формулы (3) п. 20.42 еще раз получим

arcsin = arctg - = arctg (k ctg ц).

Ятах с

Таким образом,

0 = p + --arctg(*ctgi)-yn + a. (1)

Далее, из уравнения Бернулли (4) п. 1.63, полагая c = qsin\i, найдем

о2= . (2)

+ Y-l

Следовательно, формулы (1) и (2) определяют полярные координаты q, 0 точек той характеристики в плоскости годографа, которая образует острый угол ц с вектором скорости q. Различные характеристики этого семейства можно получить, изменяя величину а. Обозначим

f{li) = li + jiTcig{kctgix)-n (3)

и заметим, что / (я -л)= -/(ц). Тогда уравнение (1) примет вид

0-/(И)=а. (4)

Соответствующее уравнение для семейства характеристик, которые образуют угол я -л с вектором скорости q, имеет вид

е + /(1А) = р. (5)

Итак, уравнения (4) и (5) представляют собой уравнения двух семейств характеристик в плоскости годографа. На характеристиках первого семейства постоянна величина а, а на характеристиках второго семейства постоянна величина р. Таким образом, аир являются некоторыми криволинейными координатами. Для заданных аир точка в поле течения определяется пересечением двух соответствующих характеристик. Каждой точке в поле течения соответствует пара чисел а, р. Следовательно, если аир известны в каждой точке течения, то течение тем самым полностью определено, потому что при этом могут быть построены характеристики и получены линии тока, как это будет объяснено ниже.

Практическое применение метода характеристик упрощается, если ввести новые обозначения. Путь D -величина 0 в градусах, Р= 1000 -[величина в градусах].

Тогда уравнения (4) и (5) можно заменить на следующие:

P + D=2A, P-D=2B, (6

где А н В -новые постоянные интегрирования. Таким образом,

Р = А-\-В, D = A-B. (7)

Заметим, что по заданному значению Р можно определить р по формуле (3), q - по формуле (2) и, следовательно, можно вычислить давление. По этой причине Буземан назвал величину Р числом, определяющим давление. Темпл *) употребил для величины D термин число, определяющее направление скорости; эта величина представляет собой угол между местным

направлением скорости течения и некоторой произвольной фиксированной линией.

Для облегчения расчетов течения воздуха (у = 1,405) по методу характеристик в нижеследующей таблице даются соответствующие значения величин Р, р/ро и л.

Таблица

20.45. Сопло с прямыми стенками. На рис. 352 показано несколько характеристик и линий тока для сверхзвукового течения внутри расширяющегося плоского сопла с прямыми стенками. Такое течение можно рассматривать как течение, вызванное источником (см. п. 8.90), помещенным в точке пересечения стенок сопла. Характеристики течения разбивают поле на ромбовидные ячейки.

Через вершину каждой ячейки проходят две характеристики; вдоль одной из них постоянна величина А, а вдоль другой постоянна величина В.

Можно провести приближенный расчет поля течения, если криволинейную сторону каждой ячейки заменить прямой линией. Криволинейная сторона, представляющая собой дугу характеристики семейства А = const, соединяет две вершины ячейки, координаты которых равны, например, величинам А, В VI А, В - г.

С некоторой степенью точности, которая зависит от малости величины е, прямая ЛИНИ11, соединяющая эти вершины ячейки, будет параллельна той характеристике семейства А = const, которая проходит через точку с координатами Л, В - у е (рис. 353). Угол между линией и местным направлением скорости течения является углом Маха, который соответствует числу, определяющему давление, Р = Л -f- В--е. Местное направление скорости течения получается по числу, определяющему направление скорости, D = = Л-В + \г.

Аналогично этому прямая линия, соединяющая точки с координатами А, В к А - г. В, будет приблизительно параллельна характеристике семейства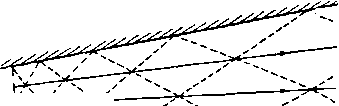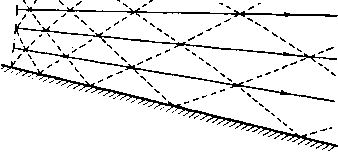

Рис. 352.

В= const, которая проходит через точку А -уе, В. Угол, который эта прямая образует с местным направлением скорости течения, является углом Маха р, который соответствует значению P = A-V В-уВ, а местное направление скорости течения определяется величиной D = А - В - ~е.

Чтобы построить диаграмму поля тече- jf ния, подобную той, которая изображена на рис. 352, следуя Темплу, предположим, что нам задана величина давления в сече- т.ш НИИ сопла V Z (рис. 354), равная р = = 0,449ро. Тогда из таблицы находим соот-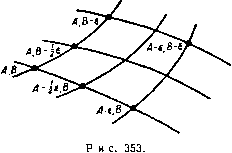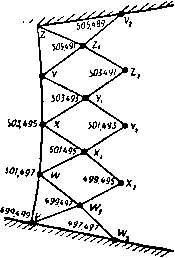

Р и с. 354.

ветствующее значение числа, определяющего давление, оно равно Р = 998. Предположим, далее, что угол между стенками сопла равен 16°. Разделим дугу VZ на четыре равные части точками W, X, Y.

Рис. 355.

отклоняется вниз от потока, имея торой прямолинейный участок ВС. Для равномерного потока угол Маха известен и определяется равенством sinno = = Cp/Vo. В рассматриваемом течении поток будет разворачиваться около угла В, начиная от прямой характеристики или линии Маха /По (рис. 355). Пред-

Примем, далее, линию стенки сопла, проходящую через точку V, в качестве начальной линии, от которой измеряются направления. Тогда числа, определяющие направление скорости, в точках V, W, X, Y, Z будут равны О, 4, 8, 12, 16. Таким образом, характеристические координаты этих точек соответственно будут (499,499), (501,497), (503,495), (505,493), (507,491).

Следующий шаг состоит в проведении линий Wi, , ttX Х^Х и т. д. Покажем, как рассчитывается одна типичная точка, например точка Х^.

Точка X лежит на характеристике А = const, проходящей через точку (501,497), и на характеристике В = const, проходящей через точку X (503,495). Следовательно, точка Xi является точкой с характеристическими координатами (501,495). Поэтому прямая UXi имеет такое же направление, что и та характеристика семейства А = const, которая проходит через точку с координатами (501,496).

Число, определяющее давление, в этой точке равно Р = 501 496 = 997, а число, определяющее направление скорости, D = 501 - 496 = 5. По таблице находим соответствующий угол Маха, он равен ц = 58°, 18. С помощью транспортира проведем через точку прямую линию, которая составляет угол D + ц = 5°-f 58°, 18 с направлением стенки, проходящей через точку V. Аналогично проведем через точку X прямую линию, имеющую то же направление, что характеристика семейства В = const, проходящая через точку с координатами (502,495). Пересечение этих двух прямых линий и определяет точку Xi. После того как рассчитаны точки Vj, ttj, Xi, Yy, Zi, можно перейти к расчету точек Wz, Xi, Yi, и т. д.

Мы проиллюстрировали расчет методом характеристик в случае сопла с прямыми стенками. Если стенки являются криволинейными, то их приближенно заменяют ломаной, у которой угол наклона двух последовательных звеньев отличается на выбранную величину е.

Применение рассмотренной схемы метода характеристик ограничено непрерывными течениями без ударных волн, на возникновение которых указывает пересечение соседних характеристик одного семейства и появление огибающей этих характеристик.

20.50. Обтекание угла. Рассмотрим поток газа, текущий с постоянной скоростью параллельно прямой стенке ЛВ. Пусть эта стенка в угловой точке В