q=(k+JyT.

Отсюда с учетом равенства (7) находим

Cp = k + R = c +R,

следовательно,

R = {Cp-c ). (8)

Гипотеза. Для совершенного газа Ср и с^ являются постоянными величинами.

Эта гипотеза также основана на результатах экспериментов.

Малую величину количества тепла мы обозначили здесь через q, а не через dQ, что казалось бы более естественным. Причина этого состоит в том, что, вообще говоря, не существует такой функции Q, полным дифференциалом которой является q. Однако можно записать равенство

q = TdS, (9)

где dS - дифференциал некоторой функции 5, которая называется энтропией.

Чтобы проверить равенство (9), заметим, что из равенств (6) и (7) с помощью соотношений (2) и (8) находим

dS = c. + -fdv = c..f + Cp.

поскольку Ср и с„ -постоянные числа, то это равенство и доказывает, что dS является полным дифференциалом. Обозначим теперь

У = Ср/с„, (10)

и тогда сразу получим

d5 = c,dln {роУ).

следует, что

dE = kdT, (5)

и тогда равенство (4) примет вид

q=kdT+pdv. (6)

Если при подводе к газу малого количества тепла q газ не имеет возможности расширяться (du = 0), то его температура возрастет, скажем, на величину dT. Тогда можно записать, что

q = c dT.

Величина с„ называется удельной теплоемкостью при постоянном объеме. Она представляет собой количество тепла, которое требуется для того, чтобы повысить температуру газа на один градус при условии, что объем газа остается постоянным. Полагая в равенстве (6) dv=0, получим

k = c . (7)

Подобным образом определим удельную теплоемкость при постоянном давлении Ср как количество тепла, которое требуется для того, чтобы повысить температуру газа на один градус, при условии, что давление газа остается постоянным. Но если р постоянно, то из соотношений (3) находим dv/v = dT/T и, следовательно, из уравнения (6) получим

и, следовательно, с точностью до произвольного слагаемого получим следующие различные формулы для внутренней энергии:

Е-==с.Т. (И,

Энтальпия, или теплосодержание, I представляет собой количество тепла, которое надо подвести к единице массы совершенного газа, чтобы при постоянном давлении поднять температуру газа от абсолютного нуля до данной температуры.

Поскольку р есть постоянная величина, то из равенства (4) имеем

=В + = = (15)

и, следовательно, из равенств (4) и (9) получим

dI = vdp+TdS. (16)

В изэнтропическом случае, когда энтропия S постоянна вдоль линии тока, но не обязательно имеет одно и то же постоянное значение на различных линиях тока, должно быть выполнено равенство

dl = - вдоль линии тока. (17)

20.10. Уравнение Крокко. Уравнение Бернулли из п. 1.62 можно записать через введенную в п. 20.01 энтальпию следующим образом:

/ = --<7* = Я вдоль линии тока. (1)

Если состояние газа изменяется от (ри Vi) до (Pi, v-i), то приращение энтропии равно

5 - S. = с. In (р^иу) - с. In (pit;y). (11)

Второй закон термодинамики утверждает, что энтропия изолированной системы не может уменьшаться, т. е. всегда dS>0.

Если энтропия сохраняет одно и то же постоянное значение во всем газе, то говорят, что такое течение является гомэнтропическим. Следовательно, условие для гомэнтропического течения таково: dS = 0. Из равенства (11) следует, что в гомэнтропическом течении

риУ = х, или pxQy, (12)

где к - постоянная, которая зависит от энтропии. Это равенство выражает закон адиабатичности (см. п. 1.62).

Установившееся течение газа подчиняется уравнениям движения и неразрывности

--lVp=(qV)q. V(Qq) = 0. (13)

Так как здесь имеются три неизвестные величины р, q, q, то этих уравнений недостаточно для определения движения. Однако в случае гомэнтропического течения можно присоединить еще уравнение адиабатичности и получить таким образом полную систему уравнений. Чтобы вычислить внутреннюю энергию, запишем

1) Fori t sky Н., У. Appl. Mech., 13 (1946), 53-60.

Функция Я называется полной энергией, или энтальпией торможения (т. е. энтальпией при q=0) для данной линии тока. Вообще говоря, Я имеет различные значения на различных линиях тока. Течение, в котором Я имеет одно и то же значение в любой точке, называется гомэнергетическим.

В случае установившегося движения при отсутствии внещних сил уравнение движения (3) п. 3.43 примет вид

qxS = v(<7) + -i-Vp. (2)

Исключая отсюда р и с помощью соотношения (16) п. 20.01 и условия (1), получим уравнение Крокко

дхе = УЯ-т. (3)

Следовательно, пренебрегая вязкостью и теплопроводностью, можно найти в поле течения вихрь в том случае, когда распределение полной энергии Я или энтропии 5 является неравномерным. Такое распределение имеет место, например, тогда, когда движение газа начинается из состояния покоя, но распределение температуры в этом состоянии является неравномерным, или тогда, когда рассматривается течение за искривленной ударной волной (см. п. 20.60).

Из уравнения (3) следует, что если установившееся безвихревое течение является гомэнергетическим, то оно будет также и гомэнтропическим и, наоборот, если такое течение является гомэнтропическим, то оно будет также и гомэнергетическим.

20.12. Наложение постоянной скорости. Пусть F представляет собой заданное плоское течение в плоскости х, у. Будем относить это течение к декартовой системе координат х, у, г, которая движется в направлении оси z равномерно со скоростью -V. Тогда течение F, которое наблюдатель видит в этой движущейся системе координат, будет отличаться в каждой точке от течения F на дополнительную постоянную скорость V, направленную нормально к плоскости последнего течения. Составляющие скорости и, v, давление, температура и плотность будут в течении F такими же функциями от х, у и времени, что и в течении F. Наложение такой постоянной скорости не влияет на ускорение частиц газа или на вихрь ).

Таким образом, наложение постоянной скорости, например, на течение для сжимаемого вихря, рассмотренное в п. 13.80, приводит к спиральному течению около оси. Линии тока здесь представляют собой спирали на соос-ных цилиндрах. Любая пара этих линий тока может быть принята в качестве границ течения. Этот пример интересен в связи с течением газа в патрубке вентилятора. Такой же способ наложения постоянной скорости можно применить при рассмотрении скользящего или стреловидного сверхзвукового крыла или косого скачка уплотнения.

20.13. Установившееся движение. Пренебрегая вязкостью, теплопроводностью и излучением, для установившегося течения газа получаем следующую систему уравнений:

уравнение неразрывности V(Qq) = 0, (1)

уравнение движения (qV)q=-~-Р< (2)

уравнение состояния р = g, S), (3)

где 5 -энтропия.

Таким образом, имеется три уравнения для четырех неизвестных q, р, q,5. Чтобы сделать задачу определенной, требуется еще четвертое уравнение. Такое уравнение получается из предположения, что течение является изэнтро-пическим. Тогда получим уравнение постоянства энтропии вдоль линии тока

(qV)5 = 0. (4)

Удобно также воспользоваться формулой

= (при 5 = const). (5)

где с -местная скорость звука (см. п. 14.86). Тогда из уравнения (3) получим

Vp=cQ+VS. (6)

Умножая обе части уравнения (6) скалярно на вектор q, найдем с помощью уравнений (4) и (1) соотношение

(qV)p = qcVe=-cQVq. (7)

Но в соответствии с формулой (IV) п. 2.34

(qV)q=V (-i-<7 )-qxS,

точно так же умножим обе части уравнения (2) скалярно на вектор q н используем соотношение (7). Поскольку векторы q и qx5 перпендикулярны, то

qV(]-9 )=caVq. (8)

Это уравнение представляет собой уравнение, которому удовлетворяет скорость; величину с* здесь можно рассматривать как величину, определенную уравнением Бернулли (4) п. 1.63

c=(Y-l)(7b.x-7). (9)

которое выполняется вдоль линии тока вследствие равенства (4).

20.20. Установившееся безвихревое движение. В этом случае имеет место уравнение (8) п. 20.13 вместе с условием q= -Уф. Отсюда в декартовых координатах находим

- ) +С - i ж+- 5-+

где

=-!. °=-0. ---f; (2)

.=4(v- [.~.-Cy-(y-(ty]-

Если величины (2) и (3) подставить в уравнение (1), то получим нелинейное уравнение, которому удовлетворяет потенциал для течения сжимаемого газа.

В случае несжимаемой жидкости (с = оо) это уравнение сводится к уравнению Лапласа.

Простые примеры установившегося безвихревого движения были уже даны для источника (п.8.90) и вихря (п. 13.80).

Значительного успеха можно добиться при помощи линеаризированной теории течений сжимаемого газа, в которой рассматриваются малые возмущения равномерного потока, создаваемые расположенным в нем тонким телом').

20.30. Метод годографа. Рассмотрим плоское установившееся движение. Пусть PQR (рт. 340)-дуга некоторой кривой в плоскости течения (х, у), которую принято называть физической плоскостью. В точках Р,

Q, R, ... проведем векторыPPi.

QQi, RRi, изображающие скорость газа в этих точках. От некоторой фиксированной точки Н отложим векторы HP, HQ,HR.....

равные и параллельные этим векторам скорости. Тогда точки Р', Q, R, ... опишут годограф данной кривой PQR. Плоскость кривой PQR называется плоскостью годографа данного движения. Если ось Ни в плоскости годографа взять параллельной оси Ох в плоскости течения, то скорость в точке Р будет равна

u + iv = qe,

а точка Р' будет иметь декартовы координаты и, v я полярные координаты q, 0.

В п. 20.20 мы видели, что потенциал скоростей безвихревого течения сжимаемого газа удовлетворяет нелинейному дифференциальному уравнению. Покажем, что если в качестве независимых переменных взять q, О или и, V, то это уравнение станет линейным.

Здесь целесообразно ввести в рассмотрение функцию тока ф. Уравнение неразрывности в случае установившегося движения имеет вид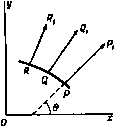

R- Q Р'

Г

Физическая пяосмап

Пмскост годографа

Рис. 340.

а (ем) , a(Qo)

= 0.

дх ду

Этому уравнению можно удовлетворить, полагая

где бо -некоторая постоянная величина, которую, например, если рассматривается обтекание крыла, удобно отождествлять с плотностью потока. Функция ф представляет собой функцию тока. Таким образом, если ф - потенциал скоростей, то имеем

- d(f = udx + vdy.

- M.dp= -vdx + udy.

1) Milne-Thomson L. M., Theoretical aerodynamics, 3rd ed., Lnd., 1958, гл. 15,20. (Линеаризированная теория течений газа излагается также в советских изданиях, например в книгах: Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, ч. 2, изд. 3, Гостекиздат, 1948; ФраикльФ. И., Карпович Е. А., Газодинамика тонких тел, Гостехиздат, 1948.-Прим. перев.)

1)Вывод уравнения Чаплыгина см., например, также в книге: За у эр Р., Введение в газовую динамику, ГИТТЛ, 1947, стр. 152-153.

[Это уравнение было приведено С. А. Чаплыгиным в 1902 г. в работе сО газовых струях (см. Чаплыгин С. А., Собр. соч., т. II, М., 1948), которая явилась основой для развития метода годографа.-Ярмж. перев.]

и отсюда, как нетрудно проверить, следуют равенства

- ( d9 + dMp = ( - iv) dz = qe- dz.

Следовательно,

dz-(d + -fdi,). (2)

Если соответствующие частные производные обозначать индексом, например, Zq = dz/dq, то тогда, очевидно,

а поскольку Zqe = ZBq, то получим

Выполняя дифференцирование, приравнивая действительную и мнимую части этого выражения и замечая, что q является функцией только от q, придем к уравнениям

Эти уравнения называются уравнениями в плоскости годографа.

Выведем уравнение, которому удовлетворяет функция тока. Поскольку Фчв = фед, то

i(f*0=*[*i(t)]

или

так как q не зависит от 9.

Но с помощью уравнения Бернулли (3) п. 1.61 и формулы с* = dp/dg получим равенство

J (Qo\ ?oi£. 5o J пп-9-Я-

\ Q J~ dp dq с* e с*

Тогда уравнение (4) примет окончательный вид

я+яи+т^,+и-т^=о, M=-f. (5)

Это уравнение, которому удовлетворяет функция тока, является линейным. Оно было получено С. А. Чаплыгиным).

20.31. Уравнение в плоскости годографа для гомэнтропического течения. Исходя из адиабатического соотношения р/ро = (q/Qo)! введем в качестве переменной безразмерную скорость

т = -, р = -Ц-(р = 2,5 для воздуха). (1)

Заметим, что 0<т<1 и что М* =2рт/(1 -т).

1) Milne-Thorn son L. М., Calculus of finite differences, Lnd., 1959, § 9.8.

*) Значительный успех в исследовании установившихся изэнтропнческих течений был достигнут С. Бергманом. См., в частности, его работы в NACA TN № 972, 973, 1018, 1096. См. также работу: Lighthill М. J., The hodograph transformation in trans-tonic flow. Proc. Roy. Soc. (A) 191 (1947), 323- 369.

Тогда нетрудно показать, что уравнение Бернулли можно представить в форме

Q = eo(l-T)P, (2)

а уравнения в плоскости годографа примут вид

2т(1-т)Р+1фт=-[1-(2р + 1)т]фе, (1-т)Рф9=2тф,. (3)

Исключая отсюда ф, придем к уравнению Чаплыгина (5) п. 20.30 в новых переменных, а именно

2т (1 -т)Р+ [2т (1 - т)-Рф.] -f [ 1 - (2р + 1) т] фее = 0. (4)

Так как это уравнение является линейным относительно ф, то его решение можно искать в виде суперпозиции элементарных решений типа

ф = BxhF (т) sin (me -f е; ), (5)

где Вт, бт -произвольные постоянные. Подстановка этого выражения в уравнение (4) приводит к гипергеометрическому уравнению

Til-x)F,n{x) + [m+\-{m + l-)x]fm{T) + -m{m + \)Fm(r) = 0, (6)

которому удовлетворяет гипергеометрическая функция)

F M-f ., 4; c;.)=l + gt-°°,+ .>>j+

где a--6 = m -р, с = т + \, аЬ = -Pm(m-l-l).

Соответствующее решение ф находится тогда из уравнения (3) и имеет вид

ф= -В^т'2т(1 т)-Р [f (T)-hm(T)] COS (mO-f-8). (7)

При m=0 или m=-1 решения получаются в замкнутой форме. Случай m = О является исключительным, и решения уравнений (3) здесь можно представить в виде

ф = Ле или ф = Ве. (8)

Отсюда следует, что соответственно ф или ф являются функциями одного только т. Решения (8) включают решения для источника (см. п. 8.90) и для вихря (см. п. 13.80) в физической плоскости, а также более общий случай спирального течения, которое получается комбинацией течений источника и вихря и было рассмотрено для несжимаемой жидкости в п. 13.33).

20.32. Случай /п=-1. В этом случае уравнение (6) п. 20.31 приобретает вид

(1-т)Г ,(х) + Р£1,(т) = 0.

F 1(т) = Л(1-т)Р+Ч-В.

Таким образом, в этом случае имеется пара фундаментальных решений

fi\(t)=l, fi>,(t) = (l-t)P+ . (1)

В соответствии с первым решением из уравнений (5) и (7) п. 20.31, в которых положим е 1 = 0 (что, очевидно, допустимо) и B i = A/2g, получим равенства

-А -А 2)

ф = s- т-V2 sin 0, ф = т-V (1 -t)-Pcos 0.

<7max 2<7max

В соответствии со вторым решением уравнения (1) получим равенства

-А 2дшах

T-V (i T)P+isin6, ф =

- А

T-V [l+(2p+l)T]cos0.

Когда 9max- оо (и, следовательно, т- -0), течения, определяемые равенствами (2) и (3), превращаются в течения несжимаемой жидкости,

определяемые формулами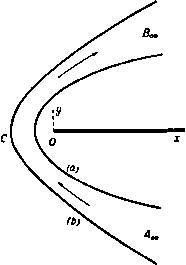

ф= -sinO,

= cos0.

Если W является комплексным потенциалом, соответствующим уравнениям (4), то

-А А dz 2qe-

2 dw

И, следовательно, vi - Az. Отсюда /Ъс = ф*-ф*, Л / = 2фф,

Рис. 341.

Таким образом, здесь линии ф = const представляют собой софокусные параболы (см. пример 20 гл. 6).

Если из этих парабол взять какие-либо две [например, (а) и {Ь) на рис. 341] в качестве границ течения, то получим течение несжимаемой жидкости в плоском канале или внутри сопла. Поперечное сечение этого сопла меняется следующим образом. Начиная от сечения Лоо, где скорость равна нулю, сопло сужается. В точке С сопло имеет самое узкое сечение, а затем расширяется до сечения 5оо, где скорость снова равна нулю. Можно ожидать, что решения (2) и (3) представляют собой течения типа, подобного в каком-то отношении вышерассмотренному течению. Течение, описываемое уравнениями (2), изучил Ринглеб'), а течение, описываемое уравнениями (3), изучил Темпл.

20.33. Течение сжимаемого газа внутри сопла, которое сначала сужается, а затем расширяется. Рассмотрим течение, которое описывается уравнениями (2) п. 20.32. Здесь удобно заменить величину А на aqx тогда

ф= - 2a(7maxf~ sin0, ф= - 2a9maiT~(l - f)-cos0. (1)

Из уравнения Бернулли в форме (2) п. 20.31 находим dф-fdф = dф--/(l-т)-P dф.

1) Ringleb F , Exakte Losungen der Differentialgleichung einer adiabatischen Gas-stromung, ZAMM, 20 (1940), 185-198.

Тогда формула (2) п. 20.30 после некоторых преобразований примет вид dz=2a [a- (l-T)-Pe2*ed0 + pT- (l-T)-P- (1 +e)dx-

- x-Ц\-x)- eЫx~ . Следовательно, после интегрирования получим формулу

-1-=т-1(1-т)-Ре29+р т-1(1-т)-Р- йт, (2)

а

где а - произвольная постоянная величина, значения которой находятся в интервале от О до 1. Выбор этой постоянной определяет только положение начала координат в физической плоскости.

Линии тока ф = const определяются путем исключения т и 9 из формулы (2) и первого из уравнений (1). Если положить

X = X (т) = ар J т-1 (1 - т)-Р- dx, (3)

а

R = Rix) = ax-{\-x)- , то из формулы (2) находим

г = Х+Ле в. (4)

Следовательно, после исключения 0 получим

{z-X)(z-X) = R\ (5)

Таким образом, линии постоянной скорости (т= const) представляют собой окружности, центры которых z = X(t) лежат на действительной оси, а радиусы равны R{x). Кроме того,

dX ар dR aT(P-f-l)-а ,g.

dx t(l-T)P+i dx t*(l-t)P+*

Следовательно, когда т увеличивается от нуля, величина X постоянно возрастает, а R уменьшается до минимального значения при т=1/(1-Ьр), а затем снова возрастает.

Условие того, чтобы две соседние окружности из семейства (5), соответствующие значениям т и т-1-бт, пересекались, состоит, как легко видеть, в следующем:

-ЙХ< 67? < бХ. Это означает, как показывают равенства (6), что

(2р-М)-1 <т< 1.

Отсюда, если воспользоваться формулами (1) п. 20.31 и (3) п. 1.63, находим

С < (7 < (7ах.

Следовательно, в сверхзвуковой области соседние окружности постоянной скорости всегда пересекаются, а в дозвуковой области, напротив, никогда не пересекаются. Критический случай имеет место тогда, когда две соседние окружности касаются друг друга. Тогда огибающая семейства (5) разделяет плоскость z на две области - одну, в которой соседние окруж-

ности ПОСТОЯННОЙ скорости пересекаются, и другую, в которой они не пересекаются.

Чтобы найти эту огибающую, продифференцируем уравнение (5) по т. Тогда с помощью равенства (4) получим

(2-f2-2X)= -2;?cos26.

Применяя затем формулы (6), находим соотношение

-:=l + P(l+cos2e).

Таким образом, огибающая семейства (5) определяется соотношением (7) и двумя уравнениями, получающимися из равенства (4).

Если в равенстве (4) рассматривать т как функцию от 9, определяемую соотношением (7), то в особой точке огибающей должно быть dz/d0= О,

что после простых преобразований дает равенство cos 29= - 1/(2Р).

Соответствующее значение т получается из соотношения (7) в виде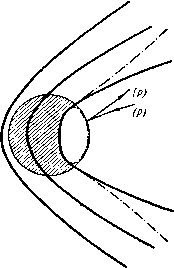

мул

Рис. 342. (1) и (7), получим для т

2р-Ь1

откуда q = c* Y2 .

В этой точке огибающей две соседние окружности касаются друг друга, и, следовательно, эта особая точка является точкой возврата. В силу симметрии имеются две такие точки возврата, расположенные симметрично относительно оси х. На рис. 342 огибающая изображена штрих-пунктирной линией.

Если в плоскости годографа взять в качестве полярных координат т и 9, то огибающая будет представлять собой эллипс, определяемый соотношением (7), а линии тока ф = const можно найти с помощью первого из уравнений (1). Исключая Э из фор-квадратное уравнение

2a2q*aai

t2-(2p-f 1)т+ 1 =0.

(9>

Таким образом, каждому значению ф здесь соответствуют два значения т; поэтому в области, где соседние окружности постоянной скорости пересекаются, получается физически невозможный характер течения. Линия тока {р), показанная на рис. 342, имеет на огибающей точку возврата. Значения т, определяемые уравнением (9), будут мнимыми при

(2р+1)2

ф2>

2р

(10)

критический случай имеет место тогда, когда в условии (10) вместо знака неравенства стоит знак равенства, т. е. при

1,342,

(11)