чину р В этих формулах надо заменить на p-\--jyiVq, где Vq выражается формулой (2) из п. 2.72.

19.42. Установившееся вращательное движение. Рассмотрим двумерное движение, представляющее собой вращение относительно оси х с угловой скоростью п, которая является функцией только расстояний S от оси вращения. Очевидно, что в этом случае скорость имеет единственную составляющую а>п, перпендикулярную к радиусу-вектору. Следовательно, все составляющие вязкого напряжения, рассмотренные в п. 19.41, кроме составляющей (ш, обращаются в нуль, а эта последняя равна \1[д{ып)/д(л -п] = = \1мдп/д(й.

Поэтому момент относительно оси вращения силы вязкого сопротивления, действующей на круговой цилиндрической поверхности радиуса ш и отнесенной к единице длины, будет равен шцо) (Зп/ш) 2п(й.

Если движение является установившимся, то момент количества движения жидкости, заключенной между двумя такими цилиндрическими поверхностями с осью z, не будет меняться во времени. Поэтому приведенная выше величина момента будет одинаковой (но противоположной по знаку) для рассматриваемых внутренней и внешней цилиндрических поверхностей. Таким образом,

где А не зависит от со. Следовательно,

п=--i + B.

Если жидкость ограничена изнутри цилиндрической поверхностью радиуса а, вращающейся с угловой скоростью л а снаружи концентрическим цилиндром радиуса Ь, вращающимся с угловой скоростью п^, то мы должны иметь

и поэтому

В этих рассуждениях не накладывается ограничения, что п, и имеют один и тот же знак. Если положить 2= - з. причем 1 и Пз имеют одинаковый знак, то угловая скорость п будет обращаться в нуль, когда

~, od ( i-b 3)

Жидкость, расположенная по разные стороны определенной таким образом заторможенной цилиндрической поверхности, будет вращаться в противоположных направлениях.

Далее, если в формуле (1) положить Ь=со и П2=0, то получим n/rii ~ а^со*, что дает распределение скорости в том случае, когда жидкость ограничена только изнутри. Если же жидкость ограничена только снаружи (но не изнутри), то а = 0 и, следовательно, п = Пг- Тогда вся система при установившемся движении будет вращаться как твердое тело.

Тейлорпоказал также, что если внешняя цилиндрическая поверхность неподвижна, а внутренняя вращается, то движение будет устойчивым только при достаточно малых угловых скоростях внутренней цилиндрической поверхности.

В более поздней статье Тейлор) показал, что если внутренняя цилиндрическая псюерхность покоится, то движение хотя и остается устойчивым в указанном выше смысле, но при достаточно большой скорости Па может наступить турбулентное движение.

19.51. Влияние вязкости на волны в воде. Когда волны малой амплитуды

т] = а sin {тх - nt)

распространяются по глубокой воде при отсутствии вязкости, комплексный потенциал (см. п. 14.17) будет а)= асе-*< - ), следовательно, комплексная скорость будет равна u - iv= шасе-*(* - >, что дает и = тасе sin {тх - nt), v= -mace cos {mx - nt).

Если же несжимаемая жидкость является вязкой, то напряжения на свободной поверхности при у = 0, соответствующие этим составляющим скорости (см. п. 19.41), равны

уу= -р--2ц = -p - 2iimac cos {mx - nt),

l* (-£ + ) = 2imacsin(/7ue-nO.

Если эти напряжения приложены к свободной поверхности как внешние воздействия, то указанная выше волна может существовать и тогда, когда жидкость является вязкой.

Работа этих напряжений в единицу времени равна

yyv + ухи = ртас cos {тх - nt) + 2цта'с',

а среднее значение этой работы составляет 2ц/п'а*с*.

Но полная энергия волны (на единицу площади ее поверхности), согласно п. 14.21, равна

agQ=amc\.

При отсутствии же упомянутых выше внешних воздействий скорость диссипации энергии волны должна равняться среднему значению работы вязких сил в единицу времени. Следовательно,

(у а /пс*о}= - 2jima c, или - 2vm*a.

1) Taylor Q. I., Phil. Trans. (A), 223 (1922). ) Taylor Q. I., Proc. Roy Soc. (A), 157 (1936).

Если внутренняя цилиндрическая поверхность покоится, то

1,2 ш2 аа

Это установившееся движение, как показал Тейлор, будет устойчивым для всех значений п^. Пара сил, обусловленная трением н действующая на внешней цилиндрической оболочке, будет в этом случае равна

Отсюда а = аоехр ( -2vm*/), где Оо -значение а в начальный момент времени. Значит, волна в момент времени t имеет профиль, определяемый выражением

т] = Оо ехр (- 2\тН) sin {тх - nt),

т. е. с течением времени амплитуда непрерывно уменьшается. Время, за которое показатель экспоненты достигает значения-1, равно

1 - o::r-L -

2vm2 8n2v

По прошествии этого времени амплитуда волны будет равна

аое-=0,37ао.

Если для воды взять значение v= 0,0178 см/сек, то получим /i = 0,711 Я* сек, где длина волны к измеряется в см.

Таким образом, при Х=\ см время ti меньше чем 1 сек, а для Я,= 100 см время 1 составляет около 2 час. Следовательно, капиллярные волны будут гаситься из-за вязкости почти немедленно, тогда как на гравитационные волны вязкость будет влиять очень мало.

19.61. Осесимметрнчное движение. Возвратимся опять к соображениям, приведенным в п. 18.50, и воспользуемся соответствующими обозначениями. Чтобы в уравнении (5) учесть вязкость, необходимо изменить левую часть этого уравнения, добавив член, соответствующий wvV X{V X S).

По формуле (4) из п. 2.72 последовательно получим

Vx={al)-1-§{ai),

0) оо) 0)

1 , д

ш да у -

о) 0)

поскольку

0) ao) У

Тогда уравнение, которому удовлетворяет функция тока, примет вид

Второй член здесь является иной формой записи определителя, входящего в уравнение (5) из п. 18.50. Этот определитель называется якобианом, или функциональным определителем; обращение его в нуль означает наличие функциональной связи между ф и а) £ф.

Отметим, что движение, которое представляется уравнением (1), является необратимым, так как прн изменении знака ф изменятся знаки первого и последнего членов этого уравнения, но знак среднего члена сохранится.

19.62. Медленные движения. Общее уравнение движения вязкой жидкости, являясь нелинейным уравнением, оказывается очень сложным, когда оно применяется не для каких-либо специальных, а для общих задач.

Это уравнение было бы линейным, если бы в нем отсутствовал квадратичный член (qV)q. Отбросив этот член, придем к следующему приближенному уравнению:

§-=-y(f+Q)+vy4 (1)

Для того чтобы получить некоторое представление о сделанном приближенном допущении, заметим, что квадратичный член, которым мы здесь пренебрегли, имеет физическую размерность U/a, где {/ - характерная скорость и а - характерная длина; например, можно рассматривать сферу радиуса а, движущуюся со скоростью U. С другой стороны, член, обусловленный вязкостью, имеет размерность \U/a. Таким образом, пренебрежение квадратичным членом сводится к предположению, что число Рейнольдса

Re = (2)

Далее, если воспользоваться формой (7) уравнения движения из п. 19.03 и пренебречь квадратичным членом - q х S, то приближенное уравнение будет иметь вид

W--(i + Y + )+- (3)

Порядок приближения здесь такой же, что и в предыдущем уравнении (1). В случае установившегося движения оба уравнения (1) и (3) можно представить как одно уравнение

vy q = yp, (4)

где скаляр Р можно рассматривать как p/Q, p/q+Q, p/g--9*--Q в соответствии с тем, пренебрегаем ли мы внешними силами и принимаем ли в качестве основного уравнения (1) или (3). Очевидно, что задача, в которой пренебрегают внешними силами, отличается от задачи, в которой они учитываются, лишь несущественными деталями, так как оба эти случая связаны с решением уравнения типа (4).

Другой и совершенно иной метод решения применил Озеен, который положил

ч = ч' + и\,

где i-единичный вектор в направлении характерной скорости U, и пренебрег квадратичными членами (qV)q.

Тогда общее уравнение движения сводится к следующему:

+ f/(iV)q- -У ( + Q)-}-vyV.

или в случае установившегося движения

i/(iV)q=-yp + vVV. (5)

Сравнивая это уравнение с уравнением (4), видим, что оно в некоторой степени учитывает квадратичные члены. О применении этого прибли-

Поэтому предпринимались попытки построить приближенные решения путем замены этого уравнения некоторым приближенным линейным уравнением. Уравнение (6) из п. 19.03 имеет вид

женного уравнения можно будет получить представление из примеров 31-34, приведенных в конце этой главы.

19.63. Медленное обтекание сферы. Пусть твердая сфера радиуса а неподвижно расположена в равномерном установившемся потоке несжимаемой жидкости; скорость потока направлена по отрицательной оси х. Если пренебречь квадратичными членами в уравнении движения, то функция тока должна удовлетворять (см. п. 19.61) уравнению

£*ф = 0. (1)

Граничные условия при этом будут таковы: на поверхности сферы

на бесконечности

-1.uZk (3)

Преобразовав уравнение (1) к полярным координатам x = rcos9, ш = г sin 0, получим

- = cose--sin9; A = sin9i-fcos9.

дж- ал лае- ~ гдв'

и уравнение (1) примет вид

г аг sine а / i a\-i\. ...

.572 + -авСже-аеЛ 1=0. (4)

Граничное условие на бесконечности ф = - i -*sin*9 показывает, что решение надо искать в виде

ф = /(г)sin*e. Подстановка этого выражения в уравнение (4) дает

(.4-l)G4-,4)w=o.

Этому линейному однородному уравнению четвертого порядка удовлетворяет сумма членов вида Лг при условии, что справедливо равенство [(л-2) (п-3)-2] [л(п-1)-2] = 0. Отсюда п = - \, 1, 2, 4, и, следовательно, общее решение имеет вид

f{r) = + Br + Cr + Dr*,

где А, В, С и D - постоянные, которые надо определить из граничных условий.

Условие (3) показывает, что С =-6/, D = 0, следовательно, ф=(-fБг-fi-f/r*)sin9.

ф=(/(-Заг + у)5ш е.

Если Р -сила сопротивления сферы, то работа, совершаемая этой силой в единицу времени, равна PU, и эта величина должна равняться скорости диссипации энергии, определенной в п. 19.21.

Вихрь выражается формулой (5) из п. 19.63; следовательно,

со я

PUndr 1 sin9.2nrsin9d9 = 6niiU4.

a 0

Таким образом,

P=6nnUa;

это соотношение носит название формулы Стокса.

Эта формула дает также величину силы, которую надо приложить к сфере, чтобы удержать ее в неподвижном состоянии в установившемся потоке скорости U.

Следует напомнить, что вышеприведенное исследование применимо только к движениям, у которых число Рейнольдса Ua/v мало. Например, в этом случае для сферы радиуса 1 мм, движущейся в воде, скорость должна быть меньше 0,2 см/сек. Основное приложение формула Стокса имеет при изучении движения мелких частиц.

Пусть сфера, состоящая из вещества с плотностью а, падает под действием силы тяжести в вязкой несжимаемой жидкости с плотностью q. Чтобы найти предельную скорость (т. е. ту скорость, при которой результирующая сила, действующая на сферу, равна нулю), надо приравнять вес сферы сумме выталкивающей силы и силы сопротивления; тогда

у лаа?д = nqag + бяцЦа, U = ag.

19.70. Векторная циркуляция. Пусть С -некоторая кривая в плоскости, в которой происходит двумерног движение, и пусть к - единичный

Составляющие скорости равны

.=FI?-f-e-(i-f)si 6.

Полагая г = а, из условия (2) получаем A = /iUa, В = -/iUa, и, таким образом,

Т -1 Т Т) Q = I г-а)Н2г+а)

Эта функция обращается в нуль при г=а. По формулам (4) и (7) из п. 2.72 определим величину вихря

19.64. Сопротивление медленно движущейся сферы. Если в только что рассмотренной задаче наложить на всю систему скорость U в направлении оси X, то жидкость станет неподвижной, а сфера будет двигаться вперед со скоростью и. Тогда соответствующая функция тока будет такой:

К= I qdr.

Если С является замкнутой кривой, ограничивающей область 2, то скалярная величина К будет представлять собой циркуляцию вдоль этой кривой (см. п. 2.42) и по теореме Стокса

/С= \ k(yxq)dS = k 5 SdS.

Если, как это обычно делается в случае плоского движения, рассматривать слой жидкости единичной толщины, то величину J dS можно назвать векторной величиной внхря в объеме dS цилиндра единичной толщины. Тогда, поскольку Z = к^, циркуляция К будет скалярной величиной вихря в объеме 2 цилиндра единичной толщины.

В более общем случае определение (1) можно распространить на незамкнутую кривую С (плоскую или пространственную), определяя циркуляцию по этой кривой С как скаляр К-

Рассмотрим теперь вектор

Г= 5 nXqdS, (2)

где интеграл берется по поверхности S. Если S является замкнутой поверхностью, которая ограничивает объем V, то по теореме Гаусса, рассматривая п как внешнюю нормаль, получаем

Г= 5 VXqdT = 5 Zdx. (3)

(V) (V)

Таким образом, Г является мерой (векторной) величины вихря в объеме V. Остается только в качестве простого упражнения показать, что для рассмотренного плоского движения, в котором через S теперь обозначим всю поверхность цилиндра с основанием 2, будем иметь К = кГ.

Определение. Вектор Г, определенный формулой (2), называется векторной циркуляцией по замкнутой или незамкнутой поверхности S.

Для векторной циркуляции по зсшкнутой поверхности о имеется еще другое полезное выражение, а именно

r = J r(nS)dS. (4)

Доказательство. Если X -любая непрерывная функция от радиуса-вектора точки, то из теоремы Стокса следует, что

5 (nxV)XdS = 0, (5)

так как любая замкнутая кривая С, проведенная на поверхности 5, делит ее на две частя S, и каждая из которых ограничена кривой С, а поверхностные интегралы по этим частям поверхности равны контурным интегралам, которые берутся по С в противоположных направлениях и поэтому уничтожаются при сложении.

вектор нормали к этой плоскости. Обозначим

V(g; q)dx=-\ (ng)qd5.

(V) (S)

Отсюда следует, что циркуляция Г остается постоянной на замкнутой поверхности, образованной вихревыми линиями, как, например, в случае сферического вихря Хилла (см. п. 18.51).

19.71. Вихревой след. Когда некоторое тело, например крыло, движется через жидкость или когда жидкость обтекает неподвижное крыло, образуется

Рис. 336.

вихревой след, который состоит из жидкости, прошедшей вблизи поверхности крыла. Вихри, как было отмечено в п. 19.11, сосредоточены в основном в той части жидкости, которая образует вихревой след (рис. 336).

Мы предполагаем изложить здесь несколько следствий, которые вытекают из двух следующих гипотез:

а) вихревой след состоит из жидкости, совершающей регулярное движение, которое может быть описано линиями тока или вихревыми линиями;

б) вне вихревого следа вихри пренебрежимо малы, т. е. можно считать, что там g = 0.

Гипотезу (б) можно рассматривать как определение вихревого следа.

Применяя диадные обозначения и формулу (2) из п. 2.71, показывающую, что единичный тензор / = V; г, будем иметь

(nxV) (q; r) = (nxV) (qo , г) + (n-f V) (q; Го) = [q (n X V)] г + -b[(n + V)q]r=q[nX(V; r)] +[n(V X q)] г = q(n x/) + 4-r(n£)= -(nxq) + r(nS).

Результат (4) получится, если проинтегрировать последнее равенство по S и воспользоваться формулой (5), где надо положить X = q; г.

Следствие. Для безвихревого движения ? = 0, и поэтому Г = 0.

Важно отметить, что приведенное выше доказательство построено так, что оно позволяет избежать рассмотрения объемных интегралов и при вычислении интеграла в выражении (4) не интересоваться тем, что происходит внутри поверхности S. Единственное ограничение прн выводе формулы (4) накладывается равенством (5), которое требует, чтобы X было ограниченной, однозначной и непрерывной функцией.

В случае замкнутой поверхности S, движущейся с жидкостью, из выражения (3) и уравнения неразрывности в форме d{Qdx)/dt - О получим скорость изменения циркуляции

(V) (V) (V)

причем здесь была использована формула (2) из п. 3.53. Но, согласно формуле (X) из п. 2.34,

V(g; q) = (SV)q-fq(VS) = (Sy)q, поскольку VS = 0; поэтому dr

19.72. Суммарный вихрь в кормовом вихревом следе. Теорема. Пусть S - замкнутая поверхность, каждая тонка которой соприкасается с жидкостью и которая пересекает вихревой след по вихревым линиям. Тогда, если скорость жидкости на S ограничена и непрерывна, то векторная циркуляция noS обращается в щ/ль.

Доказательство. По формуле (4) из п. 19.70

Г=5 r(nE)dS.

Вне вихревого следа g = О, а на участке поверхности S, проходящем внутри вихревого следа, ng = О, поскольку вихревые линии лежат на этом участке поверхности S. Следовательно, Г = О, что и требовалось доказать.

Следствие. Суммарный вихрь в любом участке вихревого следа, который вырезан с помощью некоторой замкнутой поверхности, пересекающей вихревой след по вихревым линиям, равен нулю. Действительно, по формуле (3) из п. 19.70

суммарный вихрь = g dt = Г = О,

где объемный интеграл вычисляется по всему рассматриваемому участку вихревого следа.

В этом следствии предполагается, что весь объем внутри рассматриваемой замкнутой поверхности заполнен жидкостью.

Пусть некоторая замкнутая поверхность Si содержит внутри себя крыло А и пересекает вихревой след по вихревым линиям. Рассмотрим в этом случае жидкость, находящуюся между крылом А и поверхностью Si. Тогда циркуляция по Si в силу доказанной теоремы будет равна нулю, а циркуляция по А также будет равна нулю, поскольку на крыле А в случае вязкой жидкости q = О, где q - скорость жидкости относительно А.

Таким образом, суммарный вихрь в пограничном слое и в той части вихревого следа, которая заключена внутри поверхности Si, равняется нулю.

Полученные результаты являются чисто кинематическими. Они имеют место для сжимаемой вязкой жидкости; при этом движение не предполагается установившимся.

19.73. Перенос вихрей. Обратимся к рис. 39. Пусть

Ts = 5 (nq); iS-5 v-g-dS. (1)

т т

Первый интеграл здесь представляет собой скорость переноса вихрей, обусловленную конвекцией, через незамкнутую поверхность S, а второй интеграл - скорость переноса вихрей, обусловленную диффузией.

Если на рис. 39 линию С рассматривать как вихревую линию, а диафрагму S, которая натянута на С, рассматривать как поверхность, образованную вихревыми линиями, то S можно назвать вихревой диафрагмой, натянутой на вихревую линию С.

Итак, величина Ts есть скорость переноса вихрей через вихревую диафрагму, обусловленная конвекцией и диффузией.

Теорема Престона). 5 установившемся течении однородной жидкости с одинаковой во всем потоке вязкостью скорость переноса вихрей

1) Эта теорема для случая плоского течения принадлежит Престону (Preston J. Н., А. R. С. Rep. № 6732).

через вихревую диафрагму, которая натянута на вихревую линию С, равна Ts=-J xds, х=-+4-9 + - (2)

Доказательство. Положив в уравиеиии движения (8) из п. 19.03 dqidt = О, умножим результат векторно на п и проинтегрируем noS; тогда

nx(qxS)dS + vJ nX(yxS)dS = -J (nxV)xdS.

(S) (s) (S)

Ho no формуле (II) из п. 2.32 VC = V (V X q) = О, a поскольку 5 является вихревой диафрагмой, то ng = 0. Поэтому, применяя формулу для двойного векторного произведения, будем иметь

nx(VxS) = (nxy)xE-(nV)S + n(VS) = (nxV)xS-§, nX(qxS)= -(nq)S--(nS)q= -(nq)?.

Подставим последнее выражение в уравнение (3) и воспользуемся равенством (1). Тогда по теореме Стокса

Ts=-v J (nxV)x;dS-j (nxV)xd5=-V dsxg-J dsx-

Ho контур с является вихревой линией, поэтому на С векторы ds и g параллельны, следовательно, ds х g = О, что и требовалось доказать.

19.74. Сила, действующая на крыло. Рассмотрим трехмерное крыло А, расположенное неподвижно в установившемся потоке жидкости со скоростью V=iV; массовыми силами будем пренебрегать.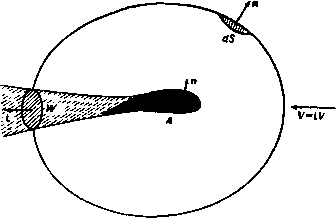

РИС. 337.

Пусть 2 - некоторая воображаемая фиксированная замкнутая поверхность (не являющаяся физической границей), которая охватывает все крыло (рис 337). Уравнение установившегося движения (1) п. 19.04 имеет вид

y[0-Q(q; q)] = 0.