причем мы применили здесь такое же преобразование, что и выше. Кроме того, бф - бф= б/С (л:), поэтому

ь ь

J 6K{x)-dx-W \ bK{x)dx = 0. -ъ -ь

Но если это равенство выполняется для любой произвольной вариации ЬК{х), то отсюда следует, что

=XU = consi = V. ду

Таким образом, вихревая пелена ведет себя как плоская пластинка шириной 2Ь, движущаяся со скоростью V в направлении, перпендикулярном к Своей длине. Накладывая скорость -У на решение, полученное в п. 6.34, будем иметь комплексный потенциал

w= -iV [z-Vr-b ), z = x4-iy, и, значит, на плоскости у=0 получим

Ф= +VVb-x\

причем знак плюс берется для верхней стороны пластинки.

Следовательно, циркуляция, соответствующая уменьшению потенциала Ф при обходе вокруг пластинки, будет равна

К{х) = 2УУЬ^-х^. Циркуляция в среднем сечении (х= 0) равна

и, таким образом,

К(х)=-!УЬ-Это выражение можно записать так:

что представляет собой уравнение эллипса, описанного точкой с координатами X, К{х)).

ПРИМЕРЫ К ГЛАВЕ 18

1. Пусть S - поверхность, ограниченная кривой С; доказать, что

[F X ds] = [п div F-grad (Fn)] dS, где через n обозначена нормаль к S.

1) Подробное обсуждение вихревых слоев в связи с теорией крыла см. в книге автора Theoretical Aerodynamics, Lnd., 1958.

ДЛЯ любой вариации К{х). Далее, согласно формуле (1) из п. 18.60,

ь

где г-расстояние между Р и элементом ds.

Показать, далее, что q = -xgTadQ/4n, где О представляет собой телесный угол, под которым данная замкнутая нить видна нз точки Р.

2. Пусть вихрь ю задан во всех точках внутри жидкости. Доказать, что значения вихря заданы правильно, если

v=rot А,

где

1 Г dT

а интеграл распространен по всей области, занятой жидкостью.

Пусть известна также дивергенция скорости 9. Показать, что это можно учесть, прибавив к написанному выше выражению для v член

4я J г

Пусть циркуляция k равна нулю по любому контуру в жидкости, за исключением таких контуров, которые охватывают тонкую вихревую нить. Доказать, что циркуляция будет одинаковой для всех контуров, которые охватывают эту вихревую нить, и что вихревая нить не может окончиться внутри жидкости. Доказать также, что

4п ] г

где векторный интеграл берется вдоль вихря.

3. Показать, что если а, Ь, с, /, g, h являются составляющими скорости чистого растяжения, то

А-=-2-ехр \ (aXa+b(i2-(-cva+2/tiv+2gvA,+2AXti)d<, С Со J

где %, ц, V - направляющие косинусы элемента <о вихревой нити.

Интерпретировать этот результат физически и рассмотреть его связь с теоремой Кельвина о сохранении циркуляции по контуру, движущемуся с жидкостью.

4. Показать, что скорость, вызванная прямолинейным участком АВ некоторой вихревой нити, перпендикулярна к плоскости РАВ и равна

4яр

(cos РЛВ-)-соз РВА),

где р-перпендикуляр, проведенный из точки Р к АВ.

Вычислить в любой точке скорость, вызванную прямоугольной вихревой нитью, если этот прямоугольник определен равенствами г = 0, и х=-±а, у = ±Ь.

5. Цилиндр произвольного сечения, содержащий жидкость, вращается с заданной угловой скоростью около своей оси, а жидкость имеет постоянный вихрь 5- Показать, что в этом движении кинетическая энергия на единицу длины цилиндра превышает кинетическую энергию безвихревого движения на величит

сС* 5 5 WV/dx)>+{dV/dy)*] dxdy.

где V-решение уравнения 7*=11 являющееся ограниченным и непрерывным во всех внутренних точках и постоянным на границе.

6. Жидкость совершает плоское движение внутри эллиптического цилиндра, оси которого 2а и 26. Доказать, что если вихрь имеет постоянное значение ш в каждой точке, то линии тока представляют собой подобные эллипсы, которые описываются за время, равное 2я (a-\-b)/(ab(o).

7. Доказать, что функция тока вида ip=Ax-\-By описывает установившееся движение идеальной жидкости с равномерно распределенным вихрем Zo- движение происходит внутри цилиндра, имеющего эллиптическое сечеиие с полуосями а, 6 и вращающегося

Неограниченная жидкость покоится на бесконечности, а движение в ней вызвано замкнутой вихревой нитью С интенсивности х; показать, что скорость в некоторой точке Р равна

4=-: [grad(l/r)xds].

вокруг своей оси с постоянной угловой скоростью (Оо, которая определяется через 5о-Показать, что траектории частиц жидкости относительно границы являются подобными эллипсами.

Воспользоваться эллиптическими координатами \, х\, связанными с декартовыми координатами х, у следующими формулами:

*=cchgcosri, y=cshsinri.

8. Доказать, что в установивщемся плоском движении жидкости с равномерно распределенным вихрем 2£ при отсутствии силы тяжести имеет место равенство

-5-=сопз1-1<7 +25ф,

где 9-скорость, а ф-функция тока.

Пусть жидкость обтекает неподвижный круговой цилиндр радиуса а. Вихрь в жидкости имеет всюду постоянное значение, равное 2. Если начало координат находится в центре сечения цилиндра, то движение на бесконечности будет движением с поперечным градиентом скоростей

и=и-21у, 0=0.

Пусть циркуляция непосредственно вокруг цилиндра равна К. Найти вид функции тока ф и доказать, что результирующая сила, приложенная к цилиндру и вызванная давлением жидкости, равна q{/(a-f-2na*q и направлена вдоль оси у.

9. Плоское движение несжимаемой жидкости таково, что вихрь имеет всюду постоянное значение 2$. Показать, что функция тока ф определяется выражением

=y S (x*+y*)+f {x+{y)+f (x-iy),

где /-произвольная функция.

Пространство между двумя софокусными цилиндрами с полуосями с ch а, с sh а и с ch В, с sh р соответственно (а > р) заполнено жидкостью с равномерно распределенным вихрем t-Определить функцию тока и доказать, что кинетическая энергия, отнесенная к единице длины, равна

ncS*c* [sh 4а-sh 4-4 th (а-Р)].

10. Цилиндрический вихревой слой таков, что вихревые линии являются образующими цилиндра, а вихрь в любой точке равен 2t/sinG, где 9-угол, измеряемый от фиксированной плоскости, проведенной через ось цилиндра. Доказать что вихревой слой будет двигаться со скоростью U, параллельной этой фиксированной плоскости.

И. Однородная жидкость соверщает круговое безвихревое плоское движение около полого цилиндрического вихря радиуса а с циркуляцией 2ях. Доказать, что давление на больших расстояниях должно равняться Qx2/(2a*).

Доказать, что вся эта система может совершать свободные колебания такого вида, что контур поперечного сечеиия вихря становится синусоидальной кривой, у которой по окружности укладывается я длин волн, и что период колебаний имеет одно из двух значений

2яа 1/2 ( Vj -j- 1) x

12. Масса жидкости, внешней границей которой служит бесконечно длинный цилиндр радиуса 6, находится в состоянии циклического безвихревого движения и испытывает действие равномерного давления Р по внешней поверхности. Доказать, что здесь должен образоваться концентрический цилиндрический канал, раднус которого а определяется уравнением

8яЗа2б2р = л1х2,

где Л1 -масса жидкости на единицу длины, а х-циркуляция.

Доказать, что если жидкость получает малое симметричное смещение, то период малых колебаний будет равен

(4я /х) аЧ [In (ft/a)/(64-a )]

13. Показать, что скорость q в некоторой точке Р в несжимаемой невязкой жидкости, простирающейся до бесконечности (где она находится в покое) и содержащей замкнутую

вихревую нить с контуром С ннтеисивиости х, будет равна q = rot Y, = У

2а

Л- 1 у- , 5г /1-3>,2 7/-8/ьз-блг

а^\2 ) 04 V 4У а* 2.4-бУ

где г < а; вычислить также скорость, когда г > а.

20. Круговая вихревая нить интенсивности х лежит на c(J)epe с радиусом / и центром О. Доказать, что этому вихрю соответствует отображенный относительно концентрической сферы радиуса а вихрь, причем этот отображенный вихрь лежит на концентрической c(J)epe радиуса /; его интенсивность равна х', а его радиус и радиус заданного вихря видны из точки О под одним и тем же углом а при условии, что

= а2, х/=-х'/Г-

Доказать, что в некоторой точке Р, лежащей на оси первого вихря Ох вне жесткой сферы с центром О и радиусом а < /, скорость направлена вдоль Ох и равна

/2 +1 a2i+i

2.ZJ V+.

Pi (cosа),

где Pi (cosa)=sin2adPj (cosa)/d(coso); Pj -зональная гармоническая функция порядка i.

21. Пусть во всех точках внутри несжимаемой жидкости задан вихрь. Тогда возможная величина скорости v определяется равенством

v = rot А,

где составляющие А таковы: 1

4я

причем интегралы берутся по всему объему, занимаемому жидкостью, а g, г\, Z, - составляющие вихря.

Найти в этой задаче связь между y и функцией тока Стокса в случае, когда контур С представляет собой окружность. Отсюда (или иным путем) вывести, что в точке Р вблизи оси составляющие скорости (параллельная и перпендикулярная к оси круговой вихревой нити) представляются соответственно выражениями

= 273-. --\гь

где ш и г-расстояния точки Р от ближайщих точек на оси и на вихревой нити соответственно.

14. Доказать, что скорость в центре кругового вихревого кольца интенсивности т и радиуса а равна т/2а; найти также скорость в любой точке на оси кольца.

15. Доказать, что действие кругового вихревого кольца на большом расстоянии от него приблизительно такое же, что и действие диполя мощности где т-интенсивность вихря и а-его радиус.

16. Вывести приближенную формулу (К/4я6) (1п (86/а) -1/4] для скорости перемещения тонкого кругового вихревого кольца; здесь 6-радиус линии центров поперечных сечений, в-радиус поперечного сечения, /С-циркуляция.

17. Пусть 9 и (/ - скорости жидкости, индуцированные тонким круговым вихревым кольцом интенсивности т и радиуса а в двух точках, находящихся в плоскости кольца на расстояниях г и г' от его центра, причем гг=а^ и г^г'. Доказать, что

я j (r rsiп2 6)/2

18. Доказать, что для тонкого вихревого кольца радиуса а функция тока в точке вблизи кольца на расстоянии х от его плоскости приближенно равна

4(а2 4-л:2)/г

где X -циркуляция вокруг кольца.

19. Доказать, что ск()рость, индуцированная тонким круговым вихревым кольцом радиуса а и интенсивности д в некоторой точке Р, расположенной в плоскости кольца на расстоянии г от его центра, равна

К / а \ /г Г / 2 Л 2

4л где

х2+ (г+а)*

4- 4-

г-расстояние точки Р от оси х, а дс-расстояние точки Р от плоскости вихревого кольца,

22. Доказать, что при определенных условиях (которые следует установить) сила и пара импульса (F, l) и кинетическая энергия системы вихрей даются выражениями

F = 0rxgdT. i.:c = Q 5 (у^+г')5х^т, Г=1е J r(gXq)dT.

Для круговой вихревой нити интенсивности х и радиуса ш с осью, направленной вдоль оси Ох, вывести выражения

где и, ti -скорости вдоль оси Ох и перпендикулярно к ней, а ф-функция тока Стокса. Для кругового вихревого кольца, поперечное сечение которого представляет собой круг радиуса а, малого по сравнению со средним радиусом щ самого кольца, вывести формулы

где S -расстояние от центра нормального сечения (круга радиуса а).

23. Тонкое вихревое кольцо совершает установившееся поступательное движение, причем закон распределения вихря имеет вид (о/ш = соо/Шо- Доказать, что если поперечное сечение кольца представляет собой круг радиуса с, центр которого находится на расстоянии Шо от оси симметрии, то скорость перемещения кольца будет равна

4я(0о

2п

(со-соо cosa) ш* ~ . -d(i>dx

С Г Г Г (<а-

сшо J L J J <(1) 4-ш1!-2(i)(i),

(() +ш5-2a)(i)ocoso4- (с-*) }/

причем интегрирование по ш и л; проводится по поперечному сечению; здесь (о представляет собой суммарный вихрь, а кольцо предполагается движущимся с постоянной скоростью в направлении оси х.

24. Показать, что для крыла конечного размаха индуктивное сопротивление будет минимальным при заданной подъемной силе в случае, когда распределение подъемной силы по размаху является эллиптическим.

Пусть V-скорость крыла относительно воздуха, l-подъемная сила, D-индуктивное сопротивление, q -плотность воздуха, 2s-размах крыла. Показать, что минимальное значение индуктивного сопротивления t) равно

Для круговой вихревой нити радиуса а и интенсивности К с осью х в качестве оси симметрии доказать, что в любой точке Р вектор А составляет прямые углы с осью х и с перпендикуляром, проведенным из точки Р к оси *. Доказать также, что модуль вектора Л равен

Глава 19 ВЯЗКОСТЬ

19.01. Тензор напряжений в идеальной жидкости. В случае идеальной жидкости сила, с которой окружающая жидкость действует на элемент dS поверхности жидкой частицы, направлена по нормали к этому элементу и равна -pndS, где п -единичная внешняя нормаль, а р -давление. Поэтому можно считать, что здесь напряжение (или сила, действующая на единицу площади) получается из тензора напряжений

W=-pl (1)

скалярным умножением на п, т. е.

напряжение = nW = - рп/ = - рп,

где / - единичный тензор (см. п. 2.16).

Если ввести три взаимно перпендикулярных единичных вектора i, j, к, то тогда / = i; i + j; j--к;к. Если в тензоре (1) диадное умножение заменить скалярным, то получим первый скалярный инвариант тензора напряжений, который обозначим через Wj:

¥х=-p(ii + jj + kk)=-Зр. (2)

Таким образом, когда задан тензор напряжений можно по выражению (2) определить давление р.

Тензор напряжений (1) обладает сферической симметрией, т. е. направление напряжения нормально к элементу dS , а его величина не зависит от ориентации dS.

19.02. Гипотеза вязкости. В случае вязкой жидкости, т. е. жидкости, подверженной внутреннему трению, напряжение на элементе dS поверхности жидкой частицы не обязательно нормально к dS и, таким образом, тензор напряжений (если допустить, что он существует) будет иметь вид

0=-p7-fH, (1)

где тензор -р7 обладает сферической симметрией, как и в случае отсутствия вязкости, а тензор S зависит непосредственно от вязкости. Тогда напряжение на элементе,dS будет равно

пФ=-pn-fnE. (2)

В п. 2.40 движение жидкой частицы было разложено на движение этой частицы как единого целого, подобно движению твердого тела, и на движение со скоростью чистого растяжения, в котором направление движения в каждой точке частицы нормально к некоторой поверхности второго порядка. Вязкость можно рассматривать как свойство, которое проявляется в виде действия сил, имеющих характер трения, на поверхности жидкой частицы, окруженной жидкостью. Ясно, что движение, подобное движению твердого тела, не вызывает относительных перемещений частиц и поэтому не может влиять на создание сил, имеющих характер трения. Поэтому в качестве естественной гипо-

тезы следует полагать, что напряжение nS в выражении (2) обусловлено только чистым растяжением.

Рассмотрим сферическую частицу с центром Р и бесконечно малым радиусом Л (рис. 334).

Если п - единичная внешняя нормаль к площадке dS поверхности частицы, то чистое растяжение заставляет площадку dS перемещаться относительно центра сферы со следующей скоростью (см. п. 2.40):

/ (Лп) =. Л (nV) q + X {V X q).

Гипотеза вязкости состоит в том, что напряжение nS пропорционально / (п), или, точнее,

nS = 2n/(n) = 2i(nV)q-bnnX(Vxq). (3)

где \1 называется коэффициентом вязкости. Физическая размерность р, выражается через размерности массы, длины и времени следующим образом: ML Т'.

Далее, из п. 2.16 имеем Рис. 334.

/(n) = (nV)q-f--n(-V;q-fq;V)=4- (: Ч + q; V). (4)

Здесь q; V есть диадное произведение, сопряженное) с диадным произведением V;q.

Тогда из равенства (3) следует, что

S=i(V; q-fq; V)

и тензор напряжений (1) принимает вид

Ф= -p/-bp(V; q-fq; V).

Теперь определим давление р как скалярный инвариант этого тензора напряжений (см. п. 19.01). а именно*)

-Зр = Ф1= 3p-f-2i(Vq).

Наконец, представим тензор напряжений в виде симметричного тензора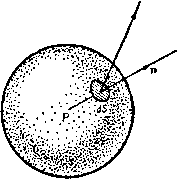

Ф= p/ 4n(Vq)/-fn(V; q-bq; V).

1) Чтобы наглядно интерпретировать и объяснить сопряженное диадное произведение q; V, выпишем V; q в полном виде и поменяем затем порядок векторов в каждом диадном произведении. Следовательно, если q = li(7i-bi2<72-t~3<73, го в декартовых координатах {*!, Х2, Хз) имеем

дХ2*дХз

(liVi-f 1272+1з'7з) = 2 (1г: 1.);. г, s=l, 2, 3,

) При этом возникает естественный вопрос о законности такого определения, поскольку давление определяется из кинетической теории газа и связано с плотностью уравнением состояния (подробности см. в приложении).-Ярил. ред.

1) См. Соре W. F., The equations of hydrodynamics in a very general form, R. and M., № 1903 (1942).

Таким образом, напряжение на площадке dS будет равно

пФ=-pn---nn(Vq) + (n2nV)q + nXn£, (6)

где 5 = V X q - вихрь.

По принятой гипотезе напряжение является линейной функцией от направления нормали к площадке, на которой, как мы предполагаем, это напряжение действует. Выбирая на поверхности сферы различные элементарные площадки, получим соответствующие вязкие напряжения. Для невязкой жидкости ц = 0. Когда жидкость покоится, то q = 0. В обоих этих случаях вязкое напряжение обращается в нуль. Вообще говоря, допустимость применения принятой выще гипотезы требует исследования передачи количества движения, обусловленного случайным движением молекул, которому в конце концов напряжение и обязано своим существованием. Однако обращение к такого рода исследованию выходит за рамки этой книги, поэтому мы просто будем предполагать, что действие внутреннего трения в жидкости описывается тензором напряжений (5).

19.03. Уравнение движения. В случае вязкой жидкости уравнение движения выводится по схеме, применявщейся уже в п. 3.41.

Таким образом, рассматривая объем жидкости V, заключенный внутри проведенной в жидкости воображаемой поверхности S , будем иметь

(V) (S) (V)

откуда, применяя теорему Гаусса, находим

+ Ш (1)

Простейщий способ вычисления УФ состоит в том, чтобы величину пФ под интегралом выразить по формуле (6) п. 19.02 и затем воспользоваться теоремой Гаусса. Тогда получим

Q-J=eF-Vp-v[i (Vq)] + IV (2nV)] q -Ь V Х (nS).

Обозначая o = Vn, легко приведем ) это уравнение к виду

-Ж=--xS+4(ч)+2(av)q-i-axg--a(Vq). (2)

В случае постоянной вязкости о = 0 и

Q = QF.-Vp-jiVxS-f4jiV(Vq), (3)

а для несжимаемой жидкости Vq = 0 и

Q# = QF-Vp-iVxS. (4)

С другой стороны, воспользовавшись формулой (V) п. 2.32, можем записать последнее уравнение в следующем виде:

=-P+ч. (5)

Во многих случаях удобнее применять кинематический коэффициент вязкости v = ц/Q, имеющий размерность L*T. Значение этого коэффициента для воды при ISC равно 1,23-10 фут^/сек (1,14-10 * смсек), а для воздуха 1,59.10 * фут^/сек (1,4810 см/сек). Судя по этим стандартным значениям, воздух является более вязким, чем вода.

В случае консервативных массовых сил, используя преобразования из п. 3.43, можно записать уравнение движения (5) следующими способами:

f==-v(f+Q)-bvV4 (6)

qxS= -v( + 4(7 + Q)-fvV4 (7)

-qxS=-Vx-vVxS, (8)

где %= p/Q + ~q-\-Q, a Q -потенциал массовых сил.

Из этого уравнения видно, что для установившегося безвихревого движения Vx = 0 и, следовательно, х имеет постоянное значение во всей жидкости.

Форма (8) удобна для преобразования уравнения движения к любой системе ортогональных криволинейных координат с помощью приемов, изложенных в п. 2.72.

В частности, из уравнения (8) для плоского движения в декартовых координатах получим

dt дх ду

В этих уравнениях скалярные величины и х не меняются при замене координат, поэтому здесь х м у можно рассматривать как любые ортогональные криволинейные координаты. Таким образом, в случае полярных координат на плоскости (г, G) имеем

дЯт у dt

Выражение для через составляющие скорости при этом будет таково:

ддв . дв ддг дг г гдЬ

19.04. Установившееся движение; отсутствие внешних сил. В этом случае уравнение (1) из п. 19.03 принимает вид

УФ = (oqV) q = V (Qq;q) - q [V (oq)].

причем здесь использована формула (X) п. 2.34. Но, согласно уравнению неразрывности, V (gq) = О и, следовательно,

V(Ф-q;q) = 0. (1)

Последнее уравнение справедливо даже в том случае, когда Q и ц являются функциями координат.

19.05. Граничные условия в вязкой жидкости. Кинематическое условие, состоящее в том, что нормальная скорость жидкости в месте соприкосновения ее с движущейся границей должна быть равна нормальной скорости этой границы, имеет место для жидкости независимо от того, является ли она вязкой или нет.

Когда вязкая жидкость находится в соприкосновении с твердым телом, касательные скорости жидкости и тела в месте соприкосновения также должны быть одинаковы. Это положение имеет характер физической гипотезы и выводится нз опыта. Таким образом, в месте соприкосновения тела и жидкости относительное движение отсутствует.

На поверхности, разделяющей две жидкости, нормальное давление и вязкое напряжение будут непрерывны при условии, что можно пренебречь поверхностным натяжением.

19.11. Уравнение, которому удовлетворяет вихрь. Применяя к уравнению (7) п. 19.03 операцию вихря и замечая, что вихрь от градиента равен нулю (см. п. 2.32), получаем в соответствии с п. 3.53

-g- = (gV)q + vVx(VV

Но по формуле (V) п. 2.32 имеем V X (Vq) = - V X (V X е) = VJ,

если при этом учесть, что, согласно п. 3.52, V=0; следовательно,

f = (SV)q + vVg. (1)

Если движение вязкой жидкости начинается из состояния покоя, то в начальный момент времени g=0 и, значит, уравнение (1) для начального момента времени имеет вид

f=vV (2)

Поскольку на границах вектор вообще говоря, не обращается в нуль, то в соответствии с последним уравнением следует, что в конце концов и внутри жидкости может образоваться вихрь в результате распространения его от границы.

В плоском движении вихрь всегда перпендикулярен плоскости движения, и поэтому в данном случае уравнение (2) применимо для любого момента времени ).

В действительных течениях жидкости вихри заметных размеров существуют только в тех областях жидкости, которые движутся вблизи твердых границ. Этот факт хорошо подтверждается наблюдениями и ярко проявляется на примере кормового следа позади плывущего корабля: след возникает только в той части воды, которая прошла вблизи корпуса корабля. Эти же наблюдения показывают, что возмущенные вихри в кормовом следе затухают вследствие трения.

Известный интерес представляет и другой пример. Время от времени возникает дискуссия относительно того, является ли направление вращения вихря, который часто можно наблюдать при вытекании воды из ванны, различным в северном и южном полушариях Земли. Нетрудно проверить экспериментально, что можно получить любое направление вращения этого вихря в зависимости оттого, наполнена ли ванна горячей или холодной водой. В горячей и в холодной воде, движущейся вблизи границы, возникают вихри противоположного направления.

) (£v)q = Sz-=0, так как q=q{*, у). -Прим. ред.