где г -вектор, определяющий положение точки Р относительно Q (но не наоборот).

Полученный выше результат показывает, что скорость в точке Р можно рассматривать как векторную сумму элементарных скоростей, каждая из которых обусловливается вихрем, находящимся в элементарном объеме dx в переменной точке Q, и равна

Соответствующее расположение векторов показано на рис. 326. Модуль этой элементарной скорости равен

dqp=-Q sin а,

где а -угол между и г. Эту элементарную скорость можно рассматривать как скорость, индуцированную в точке Р элементом, находящимся в точке Q. Рис. 326.

18.23. Вихревая нить. Пусть все вихри в жидкости сводятся к одной-едииственной вихревой нити. В п. 3.52 было доказано, что произведение величины вихря на бесконечно малую площадь поперечного сечения такой нити является постоянным. Назовем это произведение х интенсивностью вихревой нити. Скорость, индуцированная в точке Р элементом ds вихревой нити (рис. 327), будет равна

(siXr).

где si -единичный вектор касательной к вихревой нити.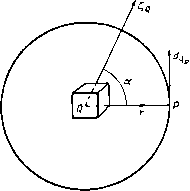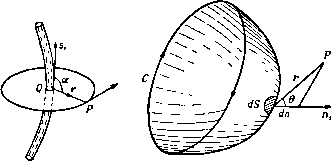

Рис. 327.

В случае замкнутой вихревой нити С (вихревое кольцо бесконечно малого поперечного сечения) будем иметь

(С) (С)

Применяя теорему Стокса в форме (3) из п. 2.51, получаем

= 5Г ( Х^)х[и(7-)]. где 5 -любая поверхность, имеющая своей границей кольцо С.

Далее, по формуле для двойного векторного произведения будем иметь

( х4)хА(Х) = { ,(Л)} {(4-)

причем последний член здесь обращается в нуль, поскольку Mr является сферической гармонической функцией. Так как dnjdQ. = д/дп, то

Отсюда следует, что скорость в точке Р выражается через потенциал скорости )

Но д{\!r)/dn = cosQ/r, где б -угол между dn и прямой, соединяющей элемент dS и точку Р. Этот угол показан на рис. 327 (заметим, что на

этом рисунке величина dr отрицательна). Далее, dScos9 представляет собой проекцию площадки dS на плоскость, перпендикулярную г, и, следо-с/ / 1 ; вательно, dScose/r = da) есть элемен-

тарный телесный угол, под которым площадка dS видна в точке Р. Таким образом, окончательно получаем

Рис. 328.

где сор -телесный угол, под которым в точке Р видна любая поверхность, ограниченная замкнутой нитью С.

Это положение иллюстрируется на рис. 328, на котором показана сфера единичного радиуса с центром в точке Р; телесный угол измеряется на поверхности этой сферы. Можно заметить, что найденная выше величина ф равна потоку через отверстие, ограниченное вихревым кольцом С, который обусловлен точечным источником мощности х/4я, находящимся в точке Р. Если точка Р описывает некоторую замкнутую кривую, которая один раз охватывает вихревое кольцо, то телесный угол при этом увеличивается или уменьшается на 4я в соответствии с выбранным направлением отсчета. Следовательно, потенциал ф является многозначной функцией. Это согласуется с тем обстоятельством, что наличие вихревого кольца делает пространство двусвязным.

Поскольку количество движения М жидкости равно интегралу Q(pdS,

который берется по обеим сторонам 5 [см. формулу (3) п. 17.20], мы имеем

= xq5 dS,

где интеграл, который одинаков для любых поверхностей, берется по одной стороне S, так как dS по замкнутой поверхности равен нулю. Если

1) Сравнивая с п. 15.26, видим, что этот потенциал является также потенциалом скорости слоя диполей, расположенных так, что оси диполей нормальны поперхности S; мощность диполей, отнесенная к единице площади, равна -х (см. п. 15.28).

вихревое кольцо представляет собой плоскую кривую с площадью А и нормалью п, то M = xQi4n.

18.24. Электромагнитная аналогия. Между формулами, полученными для вихревого движения, и формулами, относящимися к некоторым электромагнитным явлениям, имеет место точное соответствие. В этой аналогии вихревая линия соответствует электрическому контуру, интенсивность этой вихревой линии -силе тока, а скорость жидкости -магнитной силе. Таким образом, формула д;1я индуцированной скорости в точности соответствует формуле Био -Савара для магнитного эффекта электрического поля. Эту аналогию можно продолжить, заметив, что источники и стоки соответствуют положительному и отрицательному магнитным полюсам.

18.30. Кинетическая энергия. Кинетическая энергия определяется выражением

Если В -векторный потенциал, то

q = VxB, (?2 = q(VxB) = V(Bxq) + BS,

причем здесь использована формула (1) из п. 2.34. Применяя теорему Гаусса, получаем

T=~q\ BgdT-b-Q S B(nxq)d5.

(V) (S)

где первый интеграл берется по всему объему V, ограниченному поверхностью 5. Если жидкость не ограничена и первый интеграл сходится, то мы имеем

(V) (V)

где Sp, Sq -вихри в точках Р и Q, & dxp, dt - соответствующие элементарные объемы.

Для кинетической энергии можно записать и другое выражение: T=q\ q{rXZ)dT + Q\ [(nq)(qr)-4(nr)(?]dS,

(V) (S)

где первый интеграл берется по всему объему V, ограниченному поверхностью 5.

Докажем приведенный выше результат. В силу формулы для смешанного произведения трех векторов и формулы (IV) из п. 2.34 имеем

q (г Х S) = -г [q X (V X q)] = г [(qV) q] - jrVq = = (qV) (qr) - q [(qV) r] -f 1 qVr -1V (rq).

Vr = 3, (qV)r = q,

следовательно,

q (r X g) = 4 + [q (qr)] - (qr) 7q - j V (rq).

Интегрируя и применяя теорему Гаусса, получаем результат, приведенный выше, поскольку V q = 0. В случае неподвижной границы nq = 0. Если

ЖИДКОСТЬ Простирается до бесконечности, а скорость на большом расстоянии имеет порядок г *, то кинетическая энергия будет представляться лишь одним интегралом по объему.

18.40. Осесимметричные движения. Когда движение симметрично относительно оси X, вихревые линии должны быть окружностями, центры которых лежат на этой оси и плоскости которых перпендикулярны ей. Такие движения удобно рассматривать с помощью функции тока Стокса, существование которой не зависит от того, является ли движение безвихревым или нет.

Для того чтобы получить выражение для функции тока, рассмотрим в некоторой меридиональной плоскости точку Р с координатами (х, ш). Проведем через точку Р в плоскости, перпендикулярной к оси х, окружность с центром в точке М (рис. 329).

Пусть В - векторный потенциал в точке Р. Поскольку q = V X В и поскольку составляющие q лежат в меридиональной плоскости, то очевидно, что

р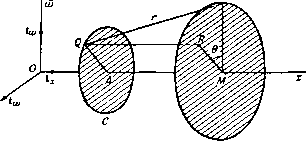

Рис. 329.

вектор В должен быть перпендикулярен к этой меридиональной плоскости. Из симметрии следует также, что векторный потенциал В имеет одну и ту же величину В в каждой точке проведенной окружности. Так как поток вектора скорости через круг радиуса со равен циркуляции вектора В по этой окружности (см. п. 18.21), то этот поток составляет 2яшВ. Если принять, что направление вихря на некоторой вихревой линии С и направление оси х связаны правилом правого винта, то указанный поток будет направлен слева направо. Таким образом, если ф - функция тока, то

2яф = - 2лсйВ, ф = - шВ.

Это выражение дает функцию тока через величину векторного потенциала.

18.41. Круговая вихревая нить. Рассмотрим круговую вихревую трубку С (см. рис. 329) весьма малого поперечного сечения а (вихревую нить). Тогда интенсивность этой нити будет, скажем, t,a = 4ях. Пусть Q - некоторая точка на окружности С с центром А, причем OA = Проведем отрезок MR, равный и параллельный AQ. Пусть угол PMR равен 9 и пусть AQ = г\. Тогда элемент дуги в точке Q будет r\dQ, а вектор вихря в Q будет направлен по касательной к С. Таким образом, вихрь в точке Q равен t cos 9- Ц-S sin9-l-, где im и 1(0 - единичные векторы оси © и перпендикуляра к меридиональной плоскости соответственно. Следовательно, по п. 18.22

I loo cos 9-U sin в

В = х \ ---r\dQ,

о

PQ = г = (л: -1)* + rf + a- 2г\а cos 9.

Коэффициент при 1 обращается в нуль по вышеуказанным причинам; в данном случае в этом легко убедиться непосредственно, выполнив интегрирование; коэффициент же при представляет собой модуль вектора В, и, следовательно, функция тока будет равна

2л

~ f cosedO

ф = - Х(ОГ]

Детальное исследование такого движения требует применения эллиптических функций. Можно, однако, заметить, что для точек, расположенных в плоскости кольца (которое рассматривается как кольцо с бесконечно малым поперечным сечением), радиальные скорости будут равны нулю. Это вытекает сразу из закона Био - Савара, упомянутого в п. 18.23. Таким образом, отсюда следует, что радиус кольца будет оставаться постоянным, а кольцо будет двигаться со скоростью, которая также должна быть постоянной, поскольку движение относительно кольца должно быть установившимся.

Если два таких вихревых кольца с одной и той же осью и одинаковым направлением вращения движутся одно за другим, то действие индуцированной скорости приводит к увеличению диаметра движущегося впереди кольца и уменьшению диаметра другого кольца. Второе кольцо может в конце концов пройти через первое, и тогда они поменяются ролями.

Если два одинаковых вихревых кольца с противоположными направлениями вращения сближаются, то индуцированная скорость будет стремиться увеличить каждое из этих колец, а на плоскости, проходящей посредине между кольцами, скорость будет перпендикулярна оси. Значит, если вихревое кольцо движется по направлению к стенке, которая параллельна плоскости этого кольца, то диаметр кольца будет непрерывно увеличиваться, а его скорость будет непрерывно уменьшаться.

18.50. Уравнение, которому удовлетворяет функция тока. Взяв вихрь от выражения (3) п. 3.43, будем иметь

f-VX(qXS) = 0. (1)

В случае осесимметричного движения

где ix, \~, iu> представляют собой единичные векторы, из которых два лежат в меридиональной плоскости, а один перпендикулярен к этой плоскости. Значит, qx g= i<7- -1~(7д.?; поэтому по формуле (4) из п. 2.72, полагая

hi= Нг= I, Лз=т, получаем

-Vx(qxS)=l.l+

и, следовательно, уравнение (1) примет вид

dl , д(д,1)

dt ~ дх dZ ~

Если воспользоваться уравнением неразрывности из п. 15.10

д(я.+ 1}==0 дх дш

ТО получим

Таким образом, введя функцию тока, будем иметь

dt \ а J 0) асо V W У W am V ш У

Для установившегося движения отсюда получим

- aw

а

4.(4-)

\ а у ды \ (й У

= 0.

Это равенство показывает, что является функцией от ф, скажем,

С = /(Ф). (3)

Уравнение (3) представляет собой соотношение, которому должен удовлетворять вихрь, для того чтобы движение было установившимся (см. п. 4.41). Далее,

дх ш V, дх да

sin со V, 0) у W

0) аш У

где

£2 =

Таким образом, из выражения (2) мы получаем уравнение, которому должна удовлетворять функция тока, а именно уравнение

(£Ф)+

аф ал:

аф асо

\ у аф V сй2 у

= 0.

Если движение является установившимся, то из соотношений (3) и (4) получается более простое уравнение:

£2ф = а2 (ф).

Представив величину = а'Е'г^ в полярных координатах, по формуле (5) из п. 2.72 получим

Таким образом, если / (ф) известна, то функция ф определяется этим дифференциальным уравнением. Сделаем самое простое предположение о виде этой произвольной функции, т. е. примем, что / (ф) = Л является постоянной величиной.

Тогда можно искать решения вида

i>=F(r) sin в.

ЧТО приводит к уравнению

rF {r)-2F {r) = Ar*.

Для того чтобы найти функцию F (г), положим А = 0, F{r) = Kr; это дает л=2 и п= -1. Такая же подстановка дает частный интеграл /г = 4, К = А/10.

Итак, имеем решение

Ф = (-+Сг+-Аг) sine.

18.51. Сферический вихрь Хилла. Только что найденная функция тока будет описывать движение внутри некоторой неподвижной сферы радиуса а, если значение ф будет оставаться конечным во всех точках внутри сферы, а нормальная скорость будет обращаться в нуль на границе. Эти условия означают, что В = О и

дУр

V. г sin 6 rdQ откуда С= -Аа/10. Итак, функция

Ф=--(a-/-2)-sin9. г<а,

удовлетворяет требуемым условиям, какова бы ни была величина А.

Вихрь, который можно найти непосредственным вычислением или по формуле (3) из п. 18.50, при этом будет равен 1 = АгsinQ. Вихревые линии будут представлять собой окружности, расположенные в плоскостях, перпендикулярных к оси симметрии. На всех таких окружностях с одинаковым радиусом вихрь имеет одинаковое значение.

В меридиональной плоскости имеются критические точки, которые определяются решениями совместных уравнений 9, = О и дв = 0, т. е.

(2a2-4r2)sinG = 0, 2 (а^ - г^) cos 9 = О,

откуда 9= + я/2, r = a/Y2. Таким образом, существует кольцо критических точек, имеющее радиус r = a/Y.

Поверхности тока определяются уравнением Рис. 330. (а'-г^) r2sin 9 = cS

где с -некоторая постоянная величина. В эти поверхности тока входят также сама сфера и ось симметрии, которые разделяют течение. Соображения о разделяющей линии тока дают тогда нам возможность построить общую форму линий тока в меридиональной плоскости (рис. 330); линии тока здесь стягиваются вокруг критических точек.

Если воспользоваться произвольностью постоянной А, то можно установить следующее интересное обстоятельство: такой вихрь может находиться в покое в окружающей жидкости, которая обтекает его. Функция тока для течения около сферы в соответствии с п. 15.30 имеет вид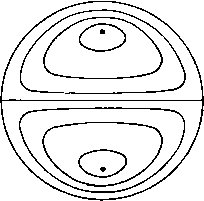

ф = /г Мп9(1-),

г>а.

При А=а уравнения (1) и (2) показывают, что г|)= О и что нормальная скорость на границе равна нулю. Для того чтобы такое движение могло существовать, должна иметь место также непрерывность касательной скорости на границе. Тогда, приравнивая величины д-1дг, получаем

И, следовательно, функция тока (1) для внутреннего движения примет вид

= --S-(a-A)Asin2e.

Если на всю рассматриваемую систему наложить скорость U, направленную слева направо, то будем иметь сферический вихрь радиуса а, движущийся со скоростью и в жидкости, которая покоится на бесконечности. Внешнее по отношению к вихрю движение жидкости является безвихревым и таким же, как движение, которое создается движущейся сферой такого же радиуса.

18.60. Крыло конечного размаха. Профиль Жуковского, изученный в гл. 7, представлял собой цилиндр бесконечной длины, у которого мы рассматривали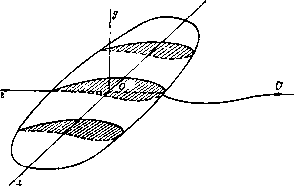

Рис. 331.

просто одно сечение. Применяемые же в действительности крылья имеют конечную длину, или размах, поэтому движение здесь нельзя считать плоским.

Рассмотрим крыло с размахом 26, симметричное относительно среднего сечения, перпендикулярного к размаху (рис. 331).. На этом рисунке крыло считается неподвижным, а поток - набегающим на переднюю кромку, причем направление потока на бесконечности вверх по течению совпадает с направлением оси Z. Ось у направлена вертикально вверх, а ось х - вдоль по размаху, начало координат находится в среднем сечении крыла. На рис. 332, который является чисто схематическим и показывает лишь основной принцип обтекания крыла, каждая линия тока, набегающая на переднюю кромку, разделяется на две линии тока: одна, s, проходит по верхней части крыла, а другая, s, проходит под крылом. Эти линии тока s и s не обязательно направлены вдоль поперечных сечений крыла, и поэтому они сходят с крыла в разных точках задней кромки.

Геометрическое место линий s будет представлять собой некоторую поверхность S , а геометрическое место линий s будет представлять собой некоторую другую поверхность S. Будем предполагать, что непосредственно за задней кромкой крыла эти поверхности совпадают и образуют одну-единственную поверхность 2 , при переходе через которую касательная скорость претерпевает разрыв по направлению, но имеет одну и ту же величину. Поскольку в урав-

нение для давления входит только квадрат величины скорости, то давление при этом будет непрерывным. Поверхность Е представляет собой вихревой слой типа, описанного в п. 13.70, и эту поверхность можно рассматривать как состоящую из распределенных по ней вихрей. Так как в любой точке поверхности 2 скорости сверху и снизу равны, то вихревые линии будут делить пополам углы между направлениями этих скоростей.

Для простоты предположим, что все эти вихревые линии являются прямыми и параллельными оси Oz. В качестве дальнейшего упрощения примем.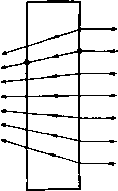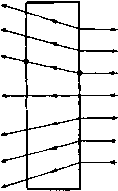

Рис. 332.

Слева - верхняя, справа - нижняя поверхность крыла.

ЧТО задняя кромка является прямой и что поверхность Е начинается у этой кромки. Эти предположения не являются столь ограничительными, как это может показаться с первого взгляда.

Для вычисления силы сопротивления ) удобнее считать, что крыло движется со скоростью и, а воздух, напротив, неподвижен. Рассмотрим две неподвижные бесконечные плоскости PaP.i, проведенные перпендикулярно к направлению движения, причем плоскость Р проведена на большом расстоянии от крыла вверх по потоку, а плоскость Pj - на большом расстоянии вниз по потоку {см. рис. 333, на котором плоскость Р не показана). Проведем вторую плоскость Р параллельную плоскости Pj и расположенную за ней на расстоянии и. Тогда приращение в единицу времени энергии жидкости, заключенной в области между плоскостями Р и Pi, будет вызвано перемещением в эту область той части вихревого слоя 2 , которая лежит между плоскостями Р[ и Pj, потому что безвихревые участки течения впереди и позади крыла не будут влиять на это приращение из-за квазистационарного характера движения между плоскостями Р и Pi. Следовательно, если ф - потенциал скорости, а R - сила сопротивления, то, приравнивая работу искомой силы R в единицу времени и скорость приращения кинетической энергии, получаем

R = -Q\]mdxdyU. (1)

Преобразуя этот интеграл с помощью формулы Грина, будем иметь

-ь -ь

1) Сопротивление, которое рассматривается здесь, является индуктивным сопротивлением, вызванным индуктивными скоростями вихревой пелены. Это сопротивление меньше, чем измеряемое в опытах сопротивление, в которое входят также поверхностное трение и другие эффекты.

где ф относится к верхней стороне 2, а ф' - к нижней стороне. Поскольку нормальная скорость ~д(р/ду непрерывна, то

о

- Ь

Рассмотрим сечение крыла, расположенное на расстоянии х от начала координат О; пусть /С (х)- циркуляция вокруг этого сечения. Когда мы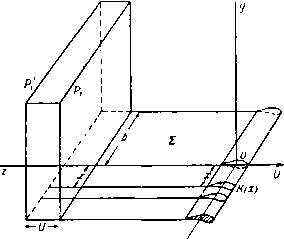

Рис. 333.

переходим через вихревой слой S сверху вниз, потенциал скорости уменьшается на величину этой циркуляции. Следовательно, ф - ф' =/С (л:). Таким образом, окончательно

ь

-ь

Вычислим подъемную силу. По теореме Кутта - Жуковского для участка крыла между х и x+dx подъемная сила равна QUK{x)dx, т. е.

Y=qU k{x)dx.

-ь

18.61. Крыло минимального индуктивного сопротивления. Теперь мы можем установить, какое распределение циркуляции К{х) вдоль крыла будет давать наименьшее сопротивление при заданной подъемной силе. Если иметь в виду обозначения предыдущего пункта, то мы должны будем определить минимум R при условии, что Y задано. Используя метод неопределенных множителей ), получаем

1) См., например, Edwards, Differential calculus. (См. также Лаврентьев М. А Люстерник Л. А., Курс вариационного исчисления, 2-е изд. ГИТТЛ, 1 960.-Прим. перев.)