= J gF, V dt = - 2 S QFb 5 dt = 2 Qi. (18)

где

QL.i=-\QFL-dr. (19)

Используя равенства (14), рассмотрим теперь следующее соотношение:

Применяя к этому соотношению оператор d/dt, получим

Ho в силу формулы (16)

] Qdt -Dt] 2 Qvvat- - ZidQi Dt+2J Dt

i i 4i

Комбинируя последнее равенство вместе с уравнениями (17), (18) и (20), получим

Поскольку величины Dqi/Dt являются независимыми, то мы можем последовательно положить их все, за исключением одной, равными нулю. Таким образом, мы получим уравнения движения для жидкости, а именно

ф-Ш- .....(>

Если положить T=Ts + Tl и сложить формулы (11) и (21), то получим

где

Q = 7s-\9r.dr. (23)

Эти уравнения представляют собой уравнения Лагранжа для всей системы, состоящей из твердых тел и жидкости.

Обобщенные силы Qt представляют собой коэффициенты, стоящие перед величинами D7 D в выражении для виртуальной мощности D (Wg + Wi)lDt, которое получается комбинацией формул (9) и (18). Единственными силами, которые надо учитывать в этом выражении для виртуальной мощности, являются внешние силы системы (третий закон Ньютона), а из других сил здесь

Пусть Fl представляет собой полную силу (включая силу давления), отнесенную к единице массы и действующую на частицу жидкости. Тогда уравнение движения имеет вид

Fl=v, (17)

а виртуальная мощность сил, действующих на жидкость, равна

надо принимать во внимание только силы давления, действующие на неподвижную поверхность Е. Однако эти последние силы не совершают работы, поскольку нормальная составляющая скорости на поверхности Е обращается в нуль. Таким образом, при вычислении обобщенных сил Qt в формуле (23) величины Fs и Fl можно рассматривать как внешние силы, действующие на твердые тела и жидкость. При отсутствии внешних сил величины Qi должны равняться нулю.

17.61. Движение сферы в присутствии стенки. Когда сфера движется в жидкости, которая ограничена бесконечной неподвижной жесткой стенкой, кинетическая энергия в первом приближении, согласно результатам, полученным в пп. 16.31 и 16.41, записывается в виде

Т={Ах + Ву),

где {х, у) - координаты центра сферы, измеряемые соответственно вдоль осей в направлении у перпендикулярно и параллельно стенке (см. рис. 322), а величины Л и В определяются формулами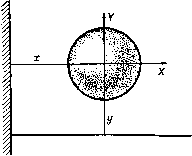

А = М+ М'

8 л:3

Рис. 322.

М' - масса жидкости, вытесненной

причем здесь 7и -масса сферы, а сферой.

Если X, К -составляющие внешних сил, действующих на сферу, то тогда уравнения Лагранжа имеют вид

-Ш^> 2 дх 2 дх

Если внешние силы таковы, что величины х, у остаются постоянными, то эти уравнения примут вид

32л:*

Х = ?( 2>+г/2), Y =

64л:4

Следовательно, если сфера движется в направлении к стенке или от нее (г/=0), то величина X будет отрицательной, и, следовательно, чтобы

сохранять величину х постоянной, потребуется сила, направленная к стенке, т. е. сфера будет отталкиваться стенкой. С другой стороны, если движение происходит параллельно стенке (л: = 0), то величина X будет положительной, и, следовательно, чтобы сохранять величину у постоянной, потребуется сила, направленная от стенки, т. е. будет притягиваться стенкой.

В случае движения двух сфер с помощью уравнений Лагранжа легко можно получить аналогичные результаты.

17.70. Тело вращения, ось которого расположена перпендикулярно направлению потока невязкой жидкости. Рассмотрим поток, имеющий скорость и и обтекающий тело вращения, которое расположено так, что его ось перпендикулярна направлению скорости этого потока.

Пусть П представляет собой плоскость, в которой лежат ось тела и направление потока. Пусть у - окружность поперечного сечения тела плоскостью, проходящей на расстоянии х от некоторой фиксированной точки на оси тела. Тогда любая точка Р поверхности S тела определяется координатами (х, со), где со - азимутальный угол, который меридиональная плоскость, проходящая через точку Р, составляет с плоскостью П.

Скорость жидкости в точке Р можно разложить на составляющую да касательную к окружности у, и составляющую q, касательную к меридиональной кривой, проходящей через точку Р. Тогда можно записать соотношения

qix, (u)=Ufix, со), qa>{x, (i)) = Ug{x, со), где функции f я g не зависят от U. Докажем, что^)

qm (X, со) = qm {х, 0) cos со, q, {х, со) = q {х, п/2) sin со.

Доказательство. Обратимся к рис. 323, где изображена точка Р, находящаяся на окружности у с центром О. Рассмотрим три случая тече-

Uf(xrw)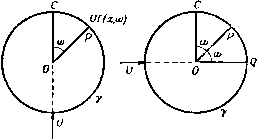

21] cot, w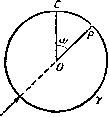

2Ucoswf(x,0)

Рис. 323.

ния. в случае (а) поток со скоростью U направлен вдоль радиуса ОС. В случае {б) поток со скоростью U направлен вдоль радиуса 0Q, причем 0Q и ОС образуют одинаковые углы с ОР. В случае (в) рассматривается поток со скоростью 2U cos со, направленный вдоль радиуса ОР.

Из соотношений (1) следует, что меридиональные составляющие скорости в точке Р в случаях (а), (б) и (в) соответственно равны Vf (х, со), Uf {х, - со)и2{ (х, 0) cos со. Но течение в случае (в) можно получить суперпозицией течений в случаях (а) и (б). Поэтому

Uf{x, (ii)+Uf{x, - со) = 2(7 cos со/0). Из условий симметрии получаем f {х, - co) = /(x, со). Следовательно, и fix, a)=Uf{x, 0) cos со.

а это доказывает, что

Чт (х, со) = q {х, 0) cos со.

Обратимся теперь к рис. 324, где точки С, Р я Q имеют тот же смысл, что и выше. Рассмотрим опять три случая течения. В случае (г) поток со скоростью и движется в направлении ОС, а в случае {д) - ъ направлении Q0. В случае (е) поток со скоростью 2U sin со движется по на-

1) Эти изящные результаты принадлежат Кэмпбеллу; Campbell I. J., Q. J. М, and A. M., IX (1956), 140-142.

правлению R0, причем радиус OR получается поворотом радиуса ОР на прямой угол по часовой стрелке. Из соотношений (1) следует, что составляющие скорости, касательные к окружности у, в точке Р в случаях {г).

ид(х,л-ш)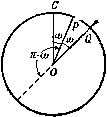

Рис. 324.

l\..2lJslna)g(x.n/2)

2Usinw

(д) и (е) соответственно равны Ug{x, ©), Ug{x, я -со) и 2U sinag{х, я/2). Поскольку течение в случае (е) получается суперпозицией течений в случаях (г) и (д), то отсюда следует, что

Ug{x, ((i) + Ug{x, n - (i)) = 2Usin(og{x, я/2).

Ho в случае (д) при обращении направления потока имеем, что g{x, n - (o) - g{x, со) и, следовательно,

<7ш {х, со) = 9и {х, я/2) sin со, что и требовалось доказать.

ПРИМЕРЫ К ГЛАВЕ 17.

1. Если ф и ф'- потенциалы скоростей двух возможных движений несжимаемой жидкости в односвязной области, то доказать, что

------- 7

где интегралы берутся по границе области.

Некоторое тело погружено в жидкость, находящуюся в неподвижной оболочке. Если тело приводится в движение со скоростью v, то доказать, что жидкости сообщается количество движения - Mv, где М-масса жидкости, вытесненной телом.

2. Определить импульсивную динаму I твердого тела, помещенного в неограниченную жидкость, не содержащую замкнутых контуров, которые не могут быть стянуты в точку. Показать, что эта импульсивная динама, вообще говоря, не совпадает с динамой количества движения жидкости.

Доказать, что динама сил, действующих со стороны тела на жидкость, эквивалентна-величине

V (vV) - ~ vK2

где обозначает динама-интеграл , V - скорость в любой точке Р достаточно большой

неподвижной поверхности Е, охватывающей тело, а V -единичный вектор внешней нормали к поверхности 2.

При каких условиях этот динама-интеграл обратится в нуль в пределе, когда все точки поверхности 2 устремляются в бесконечность?

( Динама-интеграл представляет собой предел суммы бесконечно малых скользящих векторов.)

dt V ди

дТ дТ , дТ дТ

где использованы обозначения п. 17.43, и = (ы, v, w), < = (o)i, cog, щ), V = (X, Y, Z), L = (L, M, N).

6. Эллипсоид с полуосями о, b, с движется в жидкости со скоростью и, параллельной направлению оси, имеющей длину 2а. Потенциал скорости возникающего при этом движения жидкости имеет вид

где С -некоторая постоянная величина. Определить постоянную С. Найти кинетическую энергию жидкости и импульс движения.

7. Вытянутый эллипсоид вращения с полуосями а, b установлен в потоке, имеющем скорость V в направлении, которое составляет угол 9 с большой осью эллипсоида. Определить пару, которая создается давлением жидкости и стремится повернуть эллипсоид так, чтобы его большая ось располагалась поперек потока.

(Жидкость является однородной, несжимаемой и невязкой, а внешние границы при этом отсутствуют.)

8. Показать, что если в жидкости движется тело вращения, то кинетическая энергия Т имеет вид

2Г = Л ( 2 4-г;2) -I- Са-а -f Р (0)?-f- о)) -f /?сй. Доказать, что установившееся движение, для которого

u = v=Q, w = V, (01 = 0)2=0, (03=Q,

будет устойчивым при условии, что Q2 > 4К2/С (Л -С)/Л/?2.

9. Тело вращения, у которого плотность всюду одинакова и в котором не имеется отверстий, движется в неограниченной жидкости. Пусть и, v, и) - составляющие скорости его центра массы, а (o3i, 0)2, <Вз) - угловые скорости его вращательного движения; кинетическая энергия системы при этом равна

[Ли24-в (:,2+a,2)..C(of+D ((о|+м1)].

Тело, в начальный момент времени находившееся в состоянии покоя, движется под действием силы тяжести в неограниченной жидкости. Показать, что уравнение, определяющее отклонение О оси тела относительно вертикали в любой момент времени, имеет вид

D О -I---- 2 sin 9 cos 9 = О,

где М - масса тела, которая меньше массы вытесненной жидкости.

3. Определить потенциал скорости, обусловленный сферой с центром в точке О и радиусом а движущейся со скоростью U в направлении Ох в неограниченной жидкости плотности Q.

Показать, что у жидкости, находящейся между этой сферой и любой другой концентрической сферой, составляющая количества движения по оси х равна нулю; показать также, что аналогичная составляющая количества движения жидкости, находящейся между сферой и любым бесконечно длинным круговым цилиндром с осью Ох, равна /zmU, где т - масса жидкости, вытесненная сферой.

4. Твердое тело движется без вращения в неограниченной жидкости; составляющие скорости тела, параллельные осям, равны {U, V, W), а объем тела равен v. Пусть потенциал скоростей ср возникающего при этом течения представляется на больших расстояниях от тела следующим разложением:

ax+by+cz , S2 i Sg i I Sm I

причем начало координат находится в какой-либо точке на теле, а - поверхностная сферическая гармоническая функция степени т. Показать, что кинетическая энергия Т движущейся жидкости выражается в виде

2T/Q = 4n {aU-\-bV-{-cW)-v (U+V+W).

5. Для тела, движущегося в неограниченной жидкости, вывести уравнения движе->ния в такой форме:

d Г дТ\ , дТ дТ

10. Тело вращения с плоскостью симметрии, перпендикулярной оси тела, движется со скоростью (ю, и). Показать, что для такого тела существует установившееся движение, в котором ИуСОг- 2(0=0, где ось х представляет собой ось вращения. Определить характер этого движения.

11. Кинетическая энергия тела, совершающего плоское движение в неограниченной жидкости, выражается формулой

где (и, v) - составляющие скорости центра массы тела вдоль осей Ох, Оу, связанных с телом, а 0) - угловая скорость вращения тела относительно оси Oz, перпендикулярной осям Ох и Оу. Показать, что если тело в начальный момент движется поступательно со скоростью и в направлении Ох, то в случае малых возмущений движение будет устойчивым при условии Л>В.

12. Пусть А я В - составляющие силы, которые за единицу времени сообщают сфероиду единичные скорости, направляемые соответственно перпендикулярно и параллельно оси тела, а G - соответствующая пара, которая сообщает телу единичную угловую скорость относительно оси, перпендикулярной оси тела. Пусть С есть эффективный момент инерции тела относительно оси, когда тело движется в неограниченной жидкости, покоящейся на бесконечности. Доказать, что полная кинетическая энергия Т в обычных обозначениях выражается следующей формулой:

2Г = Л (u2-f г;2)--Вш20 (p2qr2) j Cr2.

Выразить Т через лагранжевы координаты х, у, z, ср, ф и показать, что если импульс F параллелен оси Oz, тогда имеют место равенства:

а (e2-f ф2 3i 2 е) + сг f. QH+y 2г,

Оф sin2 e-j-Cr cos е = const, ф--фС059 = Г, x=-F -sin 9 cos 9 cos ф,

у- -р ---i- sin 9 cos 9 sin ф,

sin2 9 , cos2 0\

13. Маятник состоит из жесткого стержня, который свободно качается на неподвижной горизонтальной оси, проходящей через его верхний конец, и груза, который имеет форму тонкой цилиндрической эллиптической оболочки, заполненной жидкостью. Образующая этого цилиндра параллельна неподвижной оси маятника, а цилиндр имеет плоские торцы, которые составляют прямые углы с образующей. Центральная линия стержня проходит вдоль малой оси среднего поперечного сечения груза. Масса всего маятника, включая жидкость, равна М; центр массы этой системы находится на расстоянии h от неподвижной оси маятника; масса жидкости равна т. Большая и малая полуоси поперечного сечения груза равны а я b соответственно; приведенная длина этого маятника равна L, а приведенная длина маятника в том случае, если бы жидкость затвердела, равна L. Доказать равенство

(L-L) Mh (a2-f 62) = ma262.

14. Неподвижное кольцо погружено в жидкость, которая движется так, что циркуляция по любому замкнутому контуру, охватывающему кольцо, остается постоянной. Доказать, что такое движение жидкости является безвихревым и что, следовательно, циркуляция по любому замкнутому контуру, который может быть стянут в точку, равна нулю.

15. Цилиндр, массой которого можно пренебречь и сечение которого представляет собой эллипс с осями 2а и 26, наполнен водой и расположен неподвижно на столе; при этом большая ось 2а направлена вертикально. Затем цилиндр начинает катиться по столу. Найти угловую скорость цилиндра в момент, когда его большая ось принимает горизонтальное положение. Рассмотреть случаи: (I) когда стол является абсолютно шероховатым; (II) когда стол является абсолютно гладким. Показать, что квадраты угловых скоростей в этих случаях относятся как

(а2 б2): [(02-62)2-1-462 (а24-62)].

16. Внутри односвязной замкнутой поверхности находятся жидкость и тело. Эта поверхность начинает двигаться по заданному закону. Пусть - кинетическая энергия

жидкости в случае, когда тело остается свободным; Т2 - кинетическая энергия жидкости в случае, когда тело неподвижно; Т' - кинетическая энергия жидкости в случае, когда граница остается неподвижной, а тело движется так, как и в первом случае. Показать, что

T2<Ti+T.

17. Несколько сфер движется в неограниченной жидкости. Показать, что в этом случае импульс складывается из отдельных импульсов, приложенных к центру каждой сферы. Показать также, что если Т - полная кинетическая энергия всех тел и жидкости,

то тогда импульс, приложенный к центру сферы с радиусом-вектором Tq, равен dT/dtQ.

18. Два круговых цилиндра единичной длины находятся между двумя параллельными плоскостями, расстояние между которыми равно единице. Цилиндры могут скользить без трения между этими плоскостями; промежуточное пространство заполнено жидкостью. Цилиндры одновременно начинают перемещаться по направлениям, перпендикулярным плоскости, проходящей через их оси. Доказать, что цилиндры будут испытывать взаимное отталкивание или притяжение в зависимости от того, происходит ли их перемещение в противоположном или в одинаковом направлениях.

19. Две сферы движутся по линии своих центров; расстояние между центрами с велико по сравнению с радиусами сфер а и Ь. Вычислить приближенно величину кинетической энергии движения и записать уравнения движения.

Если сферы совершают малые колебания около некоторых фиксированных положений, то показать, что среднее значение силы, действующей на каждую сферу, равно 3nQ{a?b/c*)kkpi cos г, где k и k - амплитуды колебаний, 2я/р - период колебаний, е -сдвиг фаз.

Глава 18 ВИХРЕВОЕ ДВИЖЕНИЕ

18.10. Уравнение Пуассона. Пусть /q - непрерывная функция, значения которой определены в каждой точке Q, Принадлежащей объему V. Положим

где Р -точка, принадлежащая V, а dtg - элементарный объем, содержащий точку Q. Тогда фр удовлетворяет уравнению

= V4i>=-4it/p, (1)

которое называется уравнением Пуассона.

Доказательство. Рассмотрим замкнутую поверхность S, которая содержит внутри себя точку Р, ограничивает объем у и находится внутри объема V. Функцию фр можно рассматривать как потенциал скорости, вызванный непрерывно распределенными ирточниками; мощность источников, отнесенную к единице объема, обозначим через fq; таким образом, элементарному объему dxq будет соответствовать источник мощности fquxq, т. е. источник с расходом infqdxQ. Тогда поток через поверхность 5 в направлении внешней нормали будет просто равен сумме расходов всех источников, находящихся внутри поверхности S, и, следовательно,

4 л; fQdxQ=4n fpdxp.

(v) (v)

Но, согласно теореме Гаусса, поток в направлении внешней нормали равен

- J WTp-

следовательно,

\ (W + 4n/p)dTp=0,

а поскольку объем у произволен, то отсюда имеем уравнение (1), что и требовалось доказать.

Уравнение Пуассона применимо также и в том случае, когда ф и / представляют собой векторы, и имеет при этом такой вид:

д\р1д^ = V4i>= - 4Jtfp.

Действительно, каждый из векторов можно разложить на три составляющие, а затем применить формулу (1) к каждой из этих составляющих.

18.20. Выражение скорости через вихрь. Рассмотрим жидкость, заключенную внутри неподвижной оболочки Е, и предположим, что в каждой

точке задан вихрь В тех областях жидкости, где движение является безвихревым (если такие области вообще существуют), будем иметь 5=0-Если п -единичный вектор внутренней нормали для элемента dS поверхности Е, то граничное условие имеет вид

nq=0 на Е. (1)

Возьмем некоторую точку Р внутри жидкости и будем считать эту точку фиксированной. Скорость в точке Р будем обозначать через qp, а скорость в точке Q (где Q - любая другая точка в жидкости) - через qq. Рассмотрим вектор

где интеграл берется по объему V, заключенному внутри поверхности Е, а точка Р остается при этом фиксированной (рис. 325).

Здесь при дифференцировании мы будем иногда рассматривать Р как фиксированную точку, а Q -как переменную, иногда же, наоборот, мы будем рассматривать Q как фиксированную точку, а Р -как переменную. Поэтому временно заменим символ V обозначениями d/dQ или д/дР в соответствии с тем, какой случай рассматривается. Элементарный объем dx всегда будет dxQ.

Тогда, согласно уравнению Пуассона из п. 18.10,

Ри с. 325.

а^Ар арг

и, следовательно, с помощью формулы (V) из п. 2.32 получим

X

Г а

хЧ-()-

Но qQ не зависит от положения точки Р, поэтому аЛр 1

ар 4я

(V) (V)

поскольку d/dQ (1/PQ) представляет собой скорость в точке Q, вызванную единичным стоком, находящимся в точке Р, ад/дР (1/PQ)-скорость в точке Р, вызванную единичным стоком, находящимся в точке Q. Эти две скорости являются равными по величине, но противоположно направленными векторами. Далее, в силу формулы (VI) из п. 2.34 имеем

а / 4Q \ 1 3qQ д / I \

ао CpqJ~ pq

а из уравнения неразрывности следует, что dqq/dQ = 0. Поэтому

аЛр

(V) (Я)

согласно уравнению (1). Значит, равенство (3) дает

qp =

ХА,) = ХВ.

(V) (V)

(Е) (V)

Здесь четвертое выражение получено с помощью вторичного применения формулы (VII) из п. 2.34, а последнее -по теореме Гаусса в форме (2) из п. 2.61. Выведенная формула дает выражение векторного потенциала через вихрь и скорость на границе Е.

18.21. Поток через замкнутый контур. Поток через замкнутый контур С может быть выражен при помощи векторного потенциала следующим образом. Если натянуть на этот контур поверхность S, то поток будет равен

J nqdS= J n(V X В) dS.

(S) (S)

Используем формулу для смешанного произведения трех векторов п (V X В) = = (п X 7) В; тогда по теореме Стокса поток через контур С равен

\ Bds,

где интеграл берется по замкнутому контуру. Направление потока устанавливается в соответствии с правилом правого винта.

18.22. Неограниченная жидкость. Если жидкость не ограничена и если скорость на больших расстояниях имеет порядок по крайней мере l/r, где r - PQ, то интеграл по поверхности в выражении (5) из п. 18.20 стремится к нулю, поскольку dS = rdoi, где do - элементарный телесный угол. Следовательно,

= т- qi>=vxBp,

и, значит, скорость является функцией одного только вихря.

Таким образом, используя формулу (VII) из п. 2.34, будем иметь

где Bp представляет собой векторный потенциал, определяемый так:

Вр = АхАр.

Таким образом, скорость получается как вихрь от векторного потенциала подобно тому, как в безвихревом течении она получается как градиент от скалярного потенциала скорости.

Найдем векторный потенциал Bp. По определению и по формуле (VII) из п. 2.34 имеем

(V) (V)