+ XX + uX = L.

Эти уравнения представляют собой уравнения движения в форме, удобной для рассмотрения их в системе координат, оси которой фиксированы относительно движущегося тела.

17.42. Определение импульса через кинетическую энергию. Если (, К) представляют собой составляющие импульса относительно центра приведения О, то динама сил, действующая на тело в течение бесконечно малого промежутка времени бг , изменит скорости (и, <о) до значений (u-f би, &+ б<о), и тогда соответствующий импульс будет равен (Ч-б|, к+бк), причем все приращения здесь являются бесконечно малыми. В соответствии с определением импульса) совершенная при этом работа равна иб-- бЯ и она должна равняться приращению полной кинетической энергии

T = Ts+Tl.

Таким образом,

u6 + 6). = 46u-f-g-6o) = 6r, (1)

Если положить 6u = /iu, бо) = /г<!), где Л - бесконечно малая скалярная постоянная, то, поскольку импульс является однородной линейной функцией скоростей, мы должны также иметь б| = /г|, 8k = hk. Следовательно, согласно равенству (5) п. 17.21, получим

Записывая это уравнение в вариациях, находим

1) Если (F, L) - рассматриваемая динама сил, то совершенная работа равна F (ибо + L (<обг!) = U (FSO -f W (L60 = иб 4- <обЯ.

и ОВ, где

АА =(л(Ихд%, ВВ =(adtx6B.

Таким образом, скорости приращения этих векторов относительно неподвижной системы отсчета R равны соответственно о X и X Я,.

Наконец, наблюдателю, движущемуся с системой координат R, будет казаться, что векторы и Я, изменяются во времени со скоростями, которые мы будем обозначать через d%/dt и dk/dt.

Итак, скорости изменения векторов и Я, относительно неподвижной системы координат R, с которой движущаяся система координат i?мгновенно совпадает, равны соответственно

17.41. Уравнения движения. Поскольку скорость изменения импульса равна внешней силе, то в соответствии с п. 17.32 имеем

ди ды

которые выражают импульс через частные производные от полной кинетической энергии

17.43. Уравнения движения, выраженные через кинетическую энергию.

Уравнения движения, полученные в п. 17.41, можно представить теперь в виде

d / дт -\ , дТ дт \ . ,. дг , , аг

dt V a<D

Эти уравнения называются уравнениями Кирхгофа в векторной форме. Если учесть, что T = Ts + Tl, то эти уравнения можно переписать в виде

dt \ ди ди ~ dt \ ди J ди

di a© аи au dt ды J а<о au

Если бы жидкость отсутствовала {Tl = 0), то тогда правые части этих уравнений содержали бы только векторы F и L. Воздействие сил давления жидкости представляется, таким образом, остальными членами правых частей. Следовательно, воздействие жидкости представляется силой Fl и парой Ll, которые имеют вид

d Г dTL\ dTL

dt да J аи аи

17.50. Установившееся поступательное движение. Если движение является установившимся и тело не вращается, то воздействие жидкости на тело сводится к нулевой силе (парадокс Даламбера) и паре сил

-их. (1)

Эта пара (см. п. 6.42) стремится повернуть тело; она обращается в нуль тогда и только тогда, когда обращается в нуль написанное выше векторное произведение, т. е. в том случае, когда векторы и и dTJdu параллельны.

Следовательно, в этом случае скорость и направлена по нормали к эллипсоиду

dTL ди

1) Этот результат можно получить, комбинируя формулу (3) п. 17.20 и формулы (3) и (4) п. 17.21. Предоставляем читателю выполнить это в качестве упражнения.

Тогда С ПОМОЩЬЮ формулы (1) получим

Так как би и бю являются независимыми, то можем записать равенства

дТ . дТ

где с - постоянная величина). По формуле (2) п. 17.20 для о уравнение этого эллипсоида в виде

О получим (2)

Направление и может быть параллельно нормали к эллипсоиду только в том случае, когда вектор и направлен вдоль одной из главных осей эллипсоида.

Поскольку у эллипсоида имеются три главные оси, то отсюда следует, что в пространстве существуют три взаимно перпендикулярных направления,таких, что если тело движется без вращения вдоль одного из этих направлений,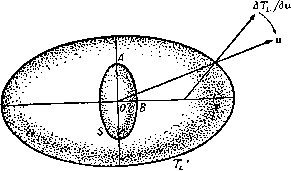

Рис. 319.

то оно будет продолжать такое движение. Эти направления называются направлениями установившегося поступательного движения.

Пусть тело движется со скоростью и по направлению установившегося поступательного движения. Пусть имеется малое возмущение, вызванное изменением скорости от величины и до и -- v и сообщением телу угловой скорости , где V и о в начальный момент времени являются бесконечно малыми. Тогда, если пренебречь членами, содержащими квадраты этих величин, то уравнения Кирхгофа станут линейными. Исследование устойчивости движения связано с решением этих уравнений и является, за исключением некоторых симметричных случаев, довольно сложным делом. Мы можем, однако, получить суждение об устойчивости движения из следующего соображения, при котором мы не будем учитывать влияние <о.

Пусть рассматриваемое тело является эллипсоидом, тогда величина Tl определяется выражением, полученным в п. 16.52. Вычисления показывают, что наибольшая ось эллипсоида (2) будет направлена по направлению наименьшей оси рассматриваемого тела - эллипсоида, и наоборот (см. рис. 319).

На этом рисунке показано также направление пары (1). Если эллипсоид S движется в направлении своей наименьшей оси ОВ, то пара (1) стремится ликвидировать любое малое отклонение движения от этого направления. Наоборот, если направление движения совпадает с наибольшей осью OA эллипсоида 5 , то эта пара будет увеличивать любое отклонение движения. Если же направление движения совпадает с направлением средней по величине оси эллипсоида S, то в зависимости от направления скорости возмущения эта пара будет либо восстанавливать это движение, либо нет. Таким образом, когда в жидкости движется тело произвольного вида, то движение будет устойчивым только в том случае, если тело движется вперед своей широкой стороной.

1) См. пример 27 г.п. 2. Упомянутый здесь эллипсоид представляет собой эллипсоид в пространстве годографа, в котором составляюшие скорости {и, v, w) являются декартовыми координатами {х, у, г).

Сделанное выше замечание дает принципиальное объяснение многим, хорошо известным явлениям. Например, для удержания корабля на курсе необходимо рулевое управление; воздушный корабль продолговатой формы также требует подобного управления. Парусный корабль при брошенном руле не будет все время идти по ветру, а будет стремиться расположиться под прямым углом к ветру. Тело, погружающееся в жидкость, стремится погружаться так, чтобы наибольший размер тела принимал горизонтальное положение.

Наконец, можно отметить, что, для того чтобы неподвижно удерживать тело в равномерном потоке со скоростью и, требуется пара

где Tl - кинетическая энергия жидкости, когда эта жидкость покоится, а тело движется со скоростью и.

Таким образом, на тело, находящееся в равномерном потоке, всегда действует пара, кроме тех случаев, когда тело ориентировано в потоке по одному из трех направлений, соответствующих направлениям установившегося поступательного движения. Этот вывод можно рассматривать как дополнение к парадоксу Даламбера.

17.51. Установившееся вращение. Когда тело находится в установившемся вращении, не совершая при этом поступательного перемещения, то и = О, а на тело действует пара с моментом

Этот момент обращается в нуль, когда векторы <о и дГ/бю параллельны, т. е. когда ось вращения параллельна нормали к эллипсоиду

дТт 1

Следовательно, существуют три оси установившегося вращения; эти оси взаимно перпендикулярны, но не обязательно пересекаются, так как указанный эллипсоид определяет только направление, а не положение этих осей.

17.52. Тело вращения. Если тело обладает тремя взаимно перпендикулярными плоскостями симметрии, то полная кинетическая энергия, отнесенная к осям, являющимся линиями пересечения этих плоскостей симметрии, должна иметь вид

2Т = Ри1 Ч- Qui + Rul +А(л1+ Bal + Cal

Действительно, при изменении знака любой составляющей скорости кинетическая энергия должна оставаться неизменной, поэтому члены, содержащие другие произведения составляющих скоростей, в это выражение не входят. Если тело является телом вращения относительно оси х, то кинетическая энергия Т не будет изменяться при перестановке Uy и и^, или со и со; следовательно, Q = R и В = С. Далее, если ось тела при движении всегда остается в плоскости X, у и вращение вокруг этой оси отсутствует, то = О, соу = = 0. Следовательно, в этом случае

Т = {Ри1 + Qul+ Сш).

Если внешние силы отсутствуют, то уравнения движения имеют вид

\Ри + ]QUy + PdizUx] - QdizUyi = О,

Ca,k + iQ-P)kUxUy = 0,

где i, j, к - единичные векторы вдоль осей координат.

Так как внешние силы отсутствуют, то уравнение (1) п. 17.32 показывает, что составляющие импульса сохраняются постоянными. В рассматриваемом случае составляющая к направлена перпендикулярно плоскости движения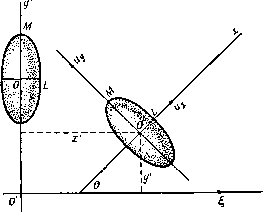

Рис. 320.

и поэтому импульс сводится к одной составляющей , которая является скользящим вектором, направленным, скажем, вдоль линии О'х' (рис. 320). Тогда

Pux = I cos 0, Quy = - g sin 0, cuj = 0,

где 0 -угол наклона линии OL с осью х', линия 0L связана с телом и совпадает с осью X.

Из уравнений (1) следует, что

C0+-~sin0cos0 = O.

Положив 1 = 20, получим

Если Р >Q, то это уравнение представляет собой уравнение движения маятника. Величина %, определяемая уравнением (4), будет периодической, так же как и величина 0, определяемая уравнением (3).

Если (х', г/) - координаты центра тела, то по формулам (2) получим

, Q Q t / cose , sin2e х' = Ux cbs 0 - Иу sm 0 = I -p- + -Q-

1 1 \ C9

y = и sin 0-f Ыу COS 0 = I\p ~~Qj sin0cos0 = -- .

При выводе последнего равенства использовано уравнение (3).

(5) (6)

Уравнение (5) показывает, что величина х никогда не становится отрицательной; следовательно, центр тела движется только вперед и траектория его не имеет петель. Из уравнения (6) получим )

У' = СЩ.

Поскольку 0 периодическая функция, то отсюда следует, что у' также является периодической функцией; поэтому траектория центра тела представляет собой

синусоиду. Последнее уравнение показывает также, что у' пропорционально 9.

Здесь могут иметь место два основных случая в зависимости от того, совершает ли тело полное вращение или совершает колебания между двумя положениями, определяемыми равенствами 0 = а и Э = -а. Оба эти случая изображены на рис. 321. В первом случае величина 9 сохраняет свой знак, поэтому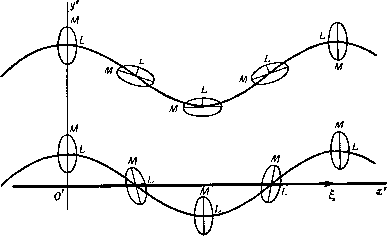

Рис. 321.

траектория не пересекает линии действия импульса. Когда же тело совершает

колебания, то величина 9 (а значит, величина у') обращается в нуль в крайних положениях и траектория располагается симметрично относительно линии действия импульса.

17.53. Устойчивость, обусловленная вращением. В случае тела вращения кинетическую энергию можно записать в виде

Г = 4(Ли + Bui + Pfl + Q + Q)-

Если тело имеет скорости ш, ico, то Ux = u, сйж = со, а при рассмотрении малых возмущений величины Uy, aty, u, to будут малыми величинами. Далее, имеем

= \Aa + \Buy + ]Bu

= iPoix + iQoiy + kQo).

1) Произвольная постоянная интегрирования здесь равна нулю, поскольку момент импульса относительно центра тела обращается в нуль при у' = 0.

dt dt

Следовательно, с точностью до величин первого порядка и^и, С0зс = -С той же степенью точности остальные уравнения примут вид

<3 + (Р-(3)сйСй,+ (Л-В) , = 0,

Q-{P-Q)(i)ay-{A-B)uuy = 0.

= 0.

Для того чтобы найти решение этих уравнений, положим Uy = ae, иг= 6е', (ду = ае*, co = Pe- Тогда получим четыре следующих уравнения:

iSKa -Bab +Au =0,

Baa +iBXb -Aua =0,

{A~B)ub +Qika +(P-Q)cop=0,

-{A-B)ua -{P-Q)aa +Qik =0.

Исключение из этих уравнений величин а, Ь, а, р приводит к определителю

iBk -За О Аи

- Всо -iBk Аи О

О (А-В) и iQk (P-Q)co

{А-В)и О (P-Q)co -iQk

Раскрывая этот определитель, получаем

[BQV - (Р - Q) Ясо^- Л (Л - В) - [В (Р - 2Q) Я-со] = 0. Отсюда получаются два квадратных уравнения для к

BQk - В {P-2Q) ка- В{Р -Q)a - А(А-В) и^ = 0, BQV+B{P-2Q)ka-B(P-Q) а'-А{А-В)и' = 0.

Условие устойчивости состоит в том, чтобы к было действительным, так как в этом случае е'* будет периодической функцией и поэтому возмущение, если оно вначале было мало, так и остается малым.

Корни обоих вышенаписанных квадратных уравнений будут действительными, если

В^ (Р - 2Q)2 со > - 4BQ [В (Р - q) со2 + Л (Л - В) и%

т. е. если

В2р2щ2 4sq -В)и'> 0.

Если Л > Б, то это условие удовлетворяется всегда, а для любых Л и Б это условие удовлетворяется только при достаточно больших значениях со.

Известным примером применения рассматриваемого здесь вопроса является устойчивость, которую придает снаряду вращение, сообщаемое нарезкой в стволе орудия.

1\ См. vnanHPHHfl КипугпАя п 17 43 -Ппии.. пр.д.

Если пренебречь произведениями малых величин, то уравнения движения по направлению оси х примут вид

1) Впервые этот результат был получен Н. Е. Жуковским (см. собр. соч., т. II). Прим. ред.

17.54. Тело, содержащее полость. Если тело имеет полость, в которой находится жидкость, совершающая ациклическое движение, то полная энергия системы будет равняться сумме энергий тела и жидкости. Предыдущие рассуждения показывают, что потенциал скорости жидкости является однородной линейной функцией от скоростей тела (и, ю), поэтому кинетическая энергия жидкости будет, очевидно, однородной квадратичной функцией от (и, (о). Таким образом, влияние жидкости, находящейся в полости внутри тела, заключается просто в изменении присоединенной массы и присоединенного момента инерции тела, а движение всей системы будет таким же, как движение данного тела, но уже с измененными значениями присоединенной массы и присоединенного момента инерции^).

17.60. Уравнения Лагранжа. Положение динамической системы считается известным, если известны координаты каждой точки этой системы, или если их по крайней мере можно определить по каким-либо другим известным величинам. Такими координатами могут быть обычные декартовы координаты X, у, Z или любые другие величины, через которые можно выразить координаты.

Например, в случае волчка, вращающегося в поле силы тяжести около фиксированной точки своей оси, достаточно знать угол наклона 0 оси волчка к вертикали и угол со, который вертикальная плоскость, проходящая через эту ось, образует с некоторой неподвижной вертикальной плоскостью. Если 0 и со заданы как функции времени и если заданы положение волчка и его движение в начальный момент времени, то можно определить положение любой точки волчка в любой момент времени t. Величины Э, со называются обобщенными координатами.

Развивая дальше эту идею, мы можем считать, что положение любой заданной динамической системы определяется некоторым числом обобщенных координат qu .....qn-

Если радиус-вектор г каждой точки системы задан явно с помощью соотношения вида

r = r(<7i, (72, qn), (1)

то говорят, что такая система является голономной. Отсюда непосредственно следует, что скорость определяется равенством

v=r=Sai7b (2)

где индекс i обозначает суммирование от t = 1 до { = п и где

ai = dr/dqi. (3)

Отсюда в силу равенства (2) имеем

Для неголономной системы равенство (2) также выполняется, но при этом, однако, соотношения (3) не имеют места; поэтому вместо уравнения (1) получается уравнение dr = 2 г^ь не являющееся уравнением в полных диффе-

г

ренциалах; таким образом, для неголономных систем, уравнение (4) больше не имеет места.

Рассмотрим теперь систему из нескольких тел S, движущуюся в невязкой жидкости L, которая может быть как неограниченной, так и ограниченной

dqi Dt

a для движения жидкости

Ф = Еф.. (8)

Для краткости мы будем называть работу, совершаемую любой системой сил в единицу времени, мощностью этих сил и будем обозначать ее для виртуальных перемещений через DW/Dt.

Рассмотрим пока только движение тел системы. Если Fs является суммарной внутренней и внешней силой, приложенной в точке Р к отдельной частице системы массы т, то виртуальная мощность сил, действующих на все тела системы, выразится с помощью соотношения (7) следующим образом:

Р Pi i

неподвижной замкнутой поверхностью Е. Мы будем предполагать, что эти тела образуют голономную систему и что движение жидкости полностью обусловлено движением тел, и это движение мгновенно прекратится, если все тела одновременно придут в состояние покоя. Тогда движение жидкости будет безвихревым и ациклическим.

Мы не можем, однако, предполагать, что жидкость представляет собой голономную систему. Поэтому если тела системы движутся циклически, т. е. каждое тело возвращается к своему первоначальному положению, то нельзя утверждать, что каждая частица жидкости при этом также вернется в свое первоначальное положение Действительно, можно построить примеры, которые, оказывается, приводят к противоположному заключению. Таким образом, мы не можем предполагать, что уравнение (1) будет иметь место и для частиц жидкости.

На поверхности тела имеется условие

где ф - потенциал скорости, а У„ - нормальная составляющая скорости на поверхности тела. На поверхности Е имеем Vn ~ 0. По предположению У„

является линейной функцией обобщенных скоростей qi, qz, qn, поэтому уравнение Лапласа и граничные условия (5) единственным образом определяют Ф как линейную функцию обобщенных скоростей. Следовательно, можно записать

Ф = S mqu (6)

г

где Фг представляют собой функции обобщенных координат (но не скоростей) и удовлетворяют уравнению Лапласа. Тогда если вычислить градиент этого потенциала, то можно увидеть, что равенство (2) будет иметь место также и для жидкости.

Рассмотрим теперь работу, совершаемую в единицу времени всеми силами системы в некотором ее виртуальном движении, в котором обобщенные виртуальные скорости (мы будем обозначать их через DqilDt) являются геометрически возможными скоростями. Тогда для точек тела имеем соотношение

Dt дт Dqi

(13)

Кинетическая энергия жидкости равна

= Qvvdt, и, следовательно, в силу уравнения (13) имеем

-?-b=QU4dT = -eUidT, (14)

dqi J dqi J

где интегралы берутся по всему объему, занятому жидкостью. В силу соотношения (8) при виртуальном движении жидкости виртуальная скорость запишется в виде

-Di--2jdr -Ж- (>

г

Поскольку операторы d/dt и D/Dt являются независимыми, то из уравнений (12) и (15) следует, что

где

Qs,=S(Fs7) (10)

р

есть обобщенная сила, соответствующая обобщенной координате qi. Уравнение движения частицы, находящейся в точке Р, имеет вид Fg = шг, и, следовательно, из формулы (10) получаем

р р р

Теперь мы воспользуемся свойством (4) голономной системы. Заменяя dridqi на drldqt и замечая, что кинетическая энергия тела равна

р

получим уравнения Лагранжа для тел системы, а именно

Рассмотрим теперь движение жидкости. Чтобы избежать недоразумений с обобщенными координатами, будем обозначать скорость жидкости через V вместо обычного обозначения q. Тогда, используя равенство (6), получим

следовательно,

дм асрг