ала ф1 в первом приближении имеем

а? cos 9

2 г2

Далее, если с велико, то в точках вблизи сферы В будем приближенно иметь г = с и, следовательно

аЗ cos 9 ar cos 6 ar cos 6

2 л2 ~ 2r3 ~ 2c3

Тогда на сфере В нормальная скорость будет равна

a3cos9 2сЗ

т. е. эта скорость не равна нулю, как это требуется по условию (1). Эту

Р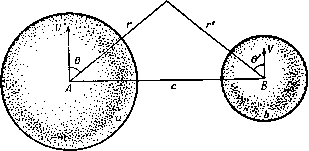

Рис. 314.

нормальную скорость можно уничтожить, если положить

аЗ cose , аЩ cos9 Ф1 = --T2- + -7i-- (2)

Таким же приближенным методом получим, что на сфере

-=COS0-~COS0.

Поэтому, если пренебречь величинами порядка c то по формуле (2) получим приближенное значение искомого потенциала скорости. Вблизи сферы В имеем

a3,-cos9 , аЗбЗ cos 9 41 = -23-4

следовательно, при г=а получим

4сЗ /-2

а при г' = Ь, получим

Ф1 = а cos 0,

(3) (4)

если пренебречь членами, содержащими с' и более высокие степени с.

Тогда кинетическая энергия жидкости, как и в п. 16.30, выражается формулой

Г = -f О Pi + (<?! + 92) иУ + PiV%

16.50. Эллипсоидальные координаты. Уравнение

где а, Ь, с фиксированы, а 0 -некоторый параметр, описывает для любого постоянного значения 0 некоторую центральную поверхность из семейства софокусных поверхностей второго порядка ). В частности, если 0 = 0, мы имеем эллипсоид. Уравнение (1) сводится к следующему:

/ (0) = X (Ь^ + 0) {с' + в) + у' {с^ + 0) (а^ + Q) + + 2 (а* -f 0) + 0) + 0) (62 + 0) (с2 + 0) = О, (2)

которое представляет собой кубическое уравнение относительно 0 и имеет, следовательно, три корня, скажем Я ц, v. Это означает, что если задана точка Р {х, у, z), то существуют три центральные поверхности второго порядка, которые проходят через эту точку Р. Эти поверхности представляют собой эллипсоид, однополостный гиперболоид и двуполостный гиперболоид. Кроме того, эти три поверхности второго порядка являются взаимно ортогональными в точке Р. За доказательством этих утверждений мы отсылаем читателя к книгам по геометрии поверхностей. Мы примем эти утверждения без доказательства.

1) См., например, Bell R. J. Т., Coordinate geometry of three dimensions, 1926, Ch. X.

где

а по теореме Грина получаем = q2.

На поверхности сферы А имеем d)i/dn= - cos 6. На поверхности сферы В имеем (5ф2/<Э = - cos 0.

Таким образом, как и в п. 16.30, получим

2 , аЧ 2

и, следовательно,

где М[ и Mj -массы жидкости, вытесненной сферами.

16.41. Сфера, движущаяся параллельно стенке. Полагая в п. 16. 40 V =и и Ь=а, получим случай сферы, движущейся параллельно фиксированной твердой плоской стенке. Действительно, плоскость, пересекающая под прямым углом линию АВ в ее середине, является плоскостью, через которую жидкость не протекает, поэтому эта плоскость может быть принята за границу течения. Если c=2h, т. е. Л -расстояние от центра сферы до стенки, то получим

г Хму.(1+.).

При этом сфера движется так, как если бы жидкость была безграничной и в ней двигалась бы еще другая сфера, являющаяся зеркальным отражением первой сферы относительно стенки.

Поскольку К, (x, V являются корнями уравнения (2), то имеет место равенство

f(0) = (;.-e)(,x-0)(v-e). (З)

Действительно, функция, стоящая в правой части, обращается в нуль, когда 6 = Х, 9=p,H6 = v, а коэффициенты при 0* справа и слева совпадают.

Если теперь поочередно положить 0 = - а*, 0 = - 6, 6 = - с*, то из равенства (3) получим

(a+ji) (g+v)

( 2 - 62) (а2-С2)

(Ь-+Х) (b+ji) (bi+v) ...

(Ь2-С2) (62 а2)

(С2 + А,) (С2+Ц) (С2 + У)

(са а2)(с2-62)

Отсюда можно найти х, у, г, если известны Я р v. Таким образом, числами Я (x, V можно пользоваться для определения положения некоторой точки в пространстве, и мы будем применять эти числа в качестве ортогональных криволинейных координат. Эти координаты называются эллипсоидальными координатами. Поверхности Я, = const, р,= const, v = const являются софокусными поверхностями второго порядка; мы всегда будем предполагать, что поверхность Я, = const представляет собой эллипсоид.

Для гидродинамических приложений требуется найти выражение для оператора \ в эллипсоидальных координатах. В соответствии с п. 2.72 сначала необходимо вычислить коэффициенты Ламэ hi, h, Лз, где

{dsf = {dxf + {dyY+{dzf = h\ {dxr+К [dY+К (rfv)

Так как

TO, полагая d(x =0, dv= 0, имеем

Из формул (4) с помощью логарифмического дифференцирования получим равенства

дх 1 X ду 1 у дг I г

таким образом, по формуле (5) найдем соотношение

1 4 L (а2 + Х)2 (624-А,)2 (С2 + А,)2 .

(а2+ц)(а2+у) ь^у.){Ь^+у)

L (а2+А,)(а2-&2)(аа с2) t zjX) (Ь^-а^) (Ь'-с^)

(С2 + (Х) (с2 + у)

(С2+А,)(С2 -а2) (c2-i

1 (Х-ц)(Х-у)

4 (а2.4-Х)(Ь2+Х)(с2+Х)

причем второе равенство получено с помощью формул (4), а третье равенство можно проверить, полагая в нем Я, равным -а', -Ь', -с' и получая отсюда отдельные слагаемые второго равенства. Выражения для коэффициентов Ла и Лз можно записать сразу же в силу симметрии.

Если рассматривать х, у, z как функции от Я, и перейти вдоль нормали от некоторой точки Р (рис. 315) на поверхности Я, = const до точки Q на

поверхности A,4-dA, = const, то получим PQ = hidk и

hi дХ

= cos8;c,

где Qx представляет собой угол между отрезком PQ и осью х. Если же, с другой стороны, рассматривать Я, как функцию от х, у, z я перейти в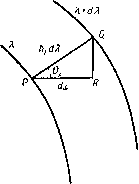

Рис. 315.

направлении х на расстояние dx, сохраняя у и z постоянными, то мы попадем в точку S на поверхности . + = const и тогда

Следовательно,

h, дк п

=COS0,.

, дХ 1 дх дх hi dl-

Если положить

то по формуле (7) находим

i2hik) ={k-i,)(k~ V), {2h2kr = (ц V) (ji - X), i2hsk.r={v-X)(v-i,).

Следовательно,

>2

(П^П^Пз) ---. 2,2,2-

Замечая, что k и kv не зависят от К, получим по формуле (3) п. 2.72 для оператора V* следующее выражение:

vф = -iK-)iy.-v) (V-X) [ -) ж ( It) +

+ (V- ) t) + i~)k.4(k.)]. (10)

Приравнивая это выражение нулю, получаем уравнение Лапласа в эллипсоидальных координатах. Функции, являющиеся решениями этого уравнения, называются эллипсоидальными гармоническими функциями.

16.51. Эллипсоидальные гармонические функции. Пользуясь обозначениями п. 16.50, можно записать уравнение Лапласа в эллипсоидальных координатах в форме

(f-) + - 0. (1)

Пусть а -некоторая функция, удовлетворяющая этому уравнению. Будем искать решения в таком виде:

где X -функция, зависящая только от к. Тогда сразу же получим равенства

д д(аг)

п or, да дх dki дХ , д^Х

Подставляя эти равенства в уравнение (1) и учитывая, что а -решение уравнения (1), получаем R = 0. Последнее равенство можно записать в следующей форме:

Поскольку с левой стороны здесь стоит функция, зависящая только от Я то правая часть не должна зависеть от (д, и v; следовательно, предложенная выше форма решения возможна лишь тогда, когда величина а удовлетворяет полученному условию. Это означает, что величина а должна иметь вид

а = ая/([А, V), (4)

где а^, не зависит от р v, а /(ц, v) не зависит от к. В этом случае равенство (3) примет вид

что после интегрирования дает

где А и S -произвольные постоянные.

Итак, если а -эллипсоидальная гармоническая функция, имеющая указанные выше свойства, то эллипсоидальными гармоническими функциями будут также и функции

? dX С dX .г.

причем вторая функция получается, если положить а = 1, поскольку а=1 является, очевидно, решением уравнения (1).

Уравнение (1) представляет собой обычное уравнение Лапласа У^Ф = О, записанное в специальной системе координат, поэтому функции х, у, 2, ху, уг, гх и любая сферическая гармоническая функция являются фактически решениями уравнения (1).

Функции X, у, г выражаются формулами (4) п. 16.50, и, следовательно, можно принять

а = (а^ + к)У^ (а + n)V!! (а^ + v) V2,

х = Сх\

я, %.

где С - произвольная постоянная, а функции х, у, z выражаются через X, ц, V по формулам (4) п. 16.50. Пределы интегрирования здесь выбраны так, чтобы при Я, = со интегралы обращались в нуль. В приложениях мы будем иметь дело только с этими функциями.

Функции типа (6) встречаются в операторах VF и г х (VV), где

г=\х + ]у + кг,

- \ W+x +62+Х +c2-f X V н

16.52. Поступательное движение эллипсоида. Рассмотрим эллипсоид Л = 0,

02 + 62 + с2 ~

движущийся в направлении оси х со скоростью U. Граничные условия в этом случае имеют вид

поскольку dn = hidX, cosQx = dx/hidX, где 0 -угол между нормалью и осью X [см. формулу (8) п. 16.50].

Таким образом, при Л=0 имеем ф= - Ux, а при Я,->схэ имеем ф- 0. Этим условиям удовлетворяет функция ф^, определяемая равенством (6) п. 16.51. Следовательно,

Ф = Сл: J

Тогда условие (2) дает

дх дх С dX Сх .

-Ж=Ж^ {а^+Х)к,-ШГ гдеХ = 0. о

Из формул (6) п. 16.50 следует dxJdX=Uxla при Я = 0, поэтому

г> аЬШ , С dX ,оч

О

Постоянная Oq зависит только от полуосей эллипсоида а, Ь, с. Для вычисления ее величины необходимо пользоваться эллиптическими интегралами.

ЧТО соответствует функции х, и

а = (6*+ A)V2 (6*+ fx)V2 (62 v)V2 (С2 + Я)2 (С2+ fi)V2 {c2 4-v)V2,

что соответствует функции yz; оба эти выражения удовлетворяют условию (4).

Таким образом, в соответствии с первой функцией (5) можно получить следующие эллипсоидальные гармонические функции:

Итак, окончательно

abcUx С dX

а на самом эллипсоиде, согласно равенству (3), имеем

aoxU

о

Кинетическая энергия жидкости в этом случае выражается в виде

Поскольку cosQxdS представляет собой проекцию элементарной площадки dS поверхности эллипсоида на плоскость х = 0 (рис. 316), то последний интеграл дает объем эллипсоида 4лаЬс/3 и, следовательно,

о

2 2-ао

где УИ-масса жидкости, вытесненной эллипсоидом.

Если положим а = Ь=с, то получаем случай сферы, при этом все интегралы вычисляются элементарно.

Когда эллипсоид имеет еще составляющие скорости V а W, параллельные осям у я z, то потенциал скорости получается суперпозицией результатов, аналогичных результату (4), и имеет вид

Рис. 316.

abcUx

abcVy Г

2-Ро J (b + k)k}.

abcWz P - Yo J

-Yo J {c + k)h

Л

где величины Po и уо можно получить, если в подинтегральной функции формулы (3) вместо а^+Х, положить Ь^к и с^ + Х,.

Сжатый и вытянутый эллипсоиды вращения можно рассматривать как частные случаи изученного выше эллипсоида общего вида.

16.53. Вращающийся эллипсоид. Если эллипсоид вращается с угловой скоростью (О = atj.i + fflyj 4-cojk, то скорость точки г = xi + r/j 4-гк на его поверхности равна о х г. Если сОу = ©г = 0, то тогда скорость равна -КгЧ-ксо^г/.

Если 9у, 0Z -углы между нормалью к эллипсоиду и осями г/ и 2, то граничное условие запишется в виде

- 5 = (- 2 cos е„ + г/ cos е^) ,

или

дХ \ дХ У дХ

Для такого вида граничного условия можно использовать функцию %2, определенную формулой (6) п. 16.51. Таким образом, полагая

Ф = Сг/2 5

(b + X){ci+X)k

получаем при Я = 0 равенство

fzt yz \ Ctjz , г f I yz /

V262 2с2 J ЬЧ-аЬс V 26 2с2 У

где принято ду/дк=Ч2у/Ь^, dzjdl = 42z/c и

о

Поскольку

1 -1 / J 1

то получим

{Ь2 - с2)аЬс

где Ро> Yo имеют тот же смысл, что и в предыдущем пункте. Тогда

(62 -с2)2

~ 2(62-c2) + (62 + c2)(Po-Yo)

а искомый потенциал скорости находится подстановкой этой величины С в формулу (1). Кинетическая энергия жидкости может быть вычислена тем же способом, который применялся выше.

Если эллипсоид имеет еще составляющие скорости соу, сог, то полный потенциал скорости находится суперпозицией результатов, получаемых по соображениям симметрии из вышеприведенных результатов.

16.54. Вращающаяся эллипсоидальная оболочка. Если внутренность эллипсоида

ai Г 63 с2 -

заполнена жидкостью и вращается относительно оси х с угловой скоростью cojc, то граничное условие имеет вид

2 дх 62 ду С2 дг ~ 62 С2 У-

Мы можем удовлетворить этому условию, полагая ф = Лг/2, так как эта функция является сферической гармонической функцией. Тогда получаем

Л (T2- + -) = x(i-)

откуда определяется величина А. Если, кроме того, оболочка имеет скорость Ых вдоль оси х, то должно иметь место равенство ф = - хи. Следовательно, если оболочка движется произвольным образом, то потенциал скорости имеет вид

ft2 c2 С2 - 2 а2 62

ц>=-хих-уиу-ги,-а,хуг-(dyZX-а ху.

ПРИМЕРЫ К ГЛАВЕ 16

1. Пусть (p = r S-сферическая гармоническая функция, причем 5 не зависит от г. Доказать, что S удовлетворяет уравнению

доказать, что 5/r +i является также сферической гармонической функцией.

+ rt(n+l)5=0,

где ц = созв. Показать, что решениями этого уравнения, соответствующими п=0 и а=1, будут Poiix), Pi(V), а также

Qo () = i- In -i±t, Qi(n) = 1 In i±-1.

Показать, что потенциал скорости линейных источников, расположенных на отрезке оси X от точки х=0 до точки х = а, равен [Qo (! ) -Qo (()]. где т -полная суммарная мощность источников, а fx=cos6, где 9 - полярный угол, причем полюс находится в точке х = а.

3. Движение жидкости задано потенциалом скорости

ф = С

Рп (cos 9),

где С-постоянная, а г н 6 - сферические координаты. Определить функцию тока.

4. Сфера радиуса а окружена концентрической сферической оболочкой радиуса Ь, а пространство между ними заполнено жидкостью. Если сфера движется со скоростью V, то показать, что потенциал скорости равен

Va3 /-

Найти также функцию тока.

5. Тонкая сферическая оболочка, массой которой можно пренебречь, окружает концентрическую сферу массы т и плотности а, промежуточное пространство заполнено жидкостью массы т' и плотности q. Доказать, что если внешней сфере сообщить нормальный импульс, то количество движения распределится между сферой и жидкостью в отношении 3me/[m (2а+б)]-

6. Пространство между двумя концентрическими сферами радиусов а л b заполнено жидкостью. Эти сферы движутся со скоростями и 1л V в одном направлении. Найтн потенциал скорости. Доказать, что кинетическая энергия жидкости равна

[аЧз V)a+2 {Ua -Vb.

Определить импульс, который требуется для приведения внешней сферы в движение со скоростью V, если массы сфер соответственно равны Mi и Мг-

7. Пространство между твердой сферой радиуса а и концентрической сферической оболочкой радиуса 2а заполнено однородной жидкостью; вся система покоится, а оболочке сообщается импульс, вызывающий ее движение со скоростью V; известно, что скорость начального движения жидкости выражается в виде (АгВ/г^} cos Q. Показать, что сфера начинает двигаться со скоростью, равной

12qV 7a+5Q

где а, Q представляют собой соответственно плотности сферы и жидкости.

Показать также, что если масса оболочки пренебрежимо мала, то величина сообщаемого импульса равна

где М-масса жидкости.

8. В полой сферической оболочке, внутренний радиус которой равен о, расположена концентрическая твердая однородная сфера радиуса b и плотности а, а пространство между двумя этими поверхностями заполнено жидкостью плотности Q. Оболочка мгновенно приходит в движение со скоростью и. Доказать, что внутренней сфере при этом сообщается скорость V, равная

и-- .

2 (a3 63) ) a3-j-26s

2. Если ф =/- 5-сферическая гармоническая функция, симметричная относительно оси X, причем 5 не зависит от г, то показать, что 5 удовлетворяет уравнению

Вычислить количество движения жидкости в начальный момент времени.

12. Сфера радиуса а и плотности а окружена концентрической сферической оболочкой радиуса Ь, а пространство между сферой и оболочкой заполнено жидкостью плотности Q. Вся система движется со скоростью v- В некоторый момент времени оболочка мгновенно останавливается. Найти скорость сферы непосредственно после удара.

13. Пространство между двумя концентрическими сферами радиусов а и 6, внешняя из которых неподвижна, заполнено жидкостью плотности Q. Показать, что если внутренняя сфера начинает двигаться иэ состояния покоя с ускорением /, то суммарная сила, действующая на внешнюю сферу, в начальный момент движения равна

2щ!аЧЗ/{Ь^~аЗ).

14. Однородная жидкость зани.мает односвязную область, ограниченную изнутри поверхностью Sj, а снаружи неподвижной поверхностью Sq. Если поверхность Si движется произвольным образом, но без изменения заключенного в ней объема, то возникает безвихревое движение жидкости. Доказать, что кинетическая энергия жидкости в этом случае больше, чем если бы внешняя граница отсутствовала.

Проверить теорему об определении кинетической энергии, когда Si и So являются мгновенно концентрическими сферами, а Si остается при движении жесткой границей.

15. Сфера радиуса а движется со скоростью v вдоль диаметра неподвижной сферы радиуса 6, пространство между двумя этими поверхностями заполнено жидкостью. Доказать, что когда расстояние между центрами сфер равняется х, то кинетическая энергия движения жидкости равна

2nQV (0+ 2 .

где

Cn,i(b-xcn) = xb-cn(x-a), Co = x.

16. Сфера массы М и радиуса а находится в состоянии покоя, причем центр ее расположен на расстоянии h от плоской границы. Показать, что величина импульса, необ-

9. Найти величины Л и В, если

есть потенциал скорости движения несжимаемой жидкости, которая заполняет пространство между твердой сферой радиуса а и концентрической сферической оболочкой радиуса 2а, когда эта сфера имеет скорость U, а оболочка покоится. Доказать, что кинетическая энергия жидкости плотности Q равна l0nQaW/2\.

Сфера, имеющая плотность сг, в начальный момент покоится и касается оболочки в ее наивысшей точке, а затем начинает падать вниз под действием силы тяжести. Показать, что скорость сферы в момент, когда она оказывается концентрической с оболочкой, выражается формулой

т - 14ga (a - Q) ~ 7а+5е

10. Пространство между твердой сферой массы М и радиуса а и неподвижной концентрической сферической оболочкой внутреннего радиуса b заполнено жидкостью. Непосредственно на сферу действует импульс /. Доказать, что сфера начинает двигаться со скоростью

где М' -масса жидкости, вытесненной сферой.

Найти для этого движения значение функции тока Стокса в начальный момент времени.

11. Жидкость плотности Q заполняет пространство между твердой сферой радиуса а а плотности а и неподвижной концентрической сферической оболочкой радиуса Ь. Доказать, что работа, которую совершает импульс, приводящий твердую сферу в движение со скоростью V, выражается формулой