Глава 16 СФЕРЫ И ЭЛЛИПСОИДЫ

16.00. Исследование безвихревого движения жидкости в пространстве в случае, когда симметрия относительно оси не имеет больше места, сводится к определению потенциала скорости, удовлетворяющего заданным краевым условиям.

Уравнение неразрывности при этом должно удовлетворяться независимо от краевых условий, иначе говоря, потенциал скорости должен удовлетворять уравнению Лапласа У^ф = 0. Функции, являющиеся решениями этого уравнения, называют гармоническими функциями; для этих функций имеется обширная литература, которую здесь невозможно даже перечислить. Мы рассмотрим здесь некоторые специальные типы решения уравнения Лапласа, которые будут непосредственно применимы к исследованию движения двух сфер и эллипсоида.

16.10. Сферические гармонические функции. Уравнение Лапласа в декартовых координатах имеет вид

Любое однородное решение этого уравнения представляет собой функцию, которая называется сферической гармонической функцией. Очевидными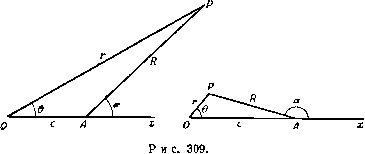

примерами таких решений являются функции 1, х, у, г, уг, х^ - у^. Если Ф есть некоторая гармоническая функция, такая, чтоф = фт + ф„, где ф^ и ф„ - однородные функции от х, у, z разных степеней m и соответственно, то очевидно, что ф^ и ф„ также являются сферическими гармоническими функциями, поскольку в результате применения к этим функциям оператора получаются также однородные функции разных степеней, и, следо вательно, они не могут взаимно уничтожиться при сложении.

Уравнение Лапласа в полярных координатах г, 6, ю, согласно п. 2.72, принимает вид

i(=)+s-Eew(-et) + jJreS = - (2)

Ф = г cos 0 Ч- cos о) = UrPi (cos 0) +

Pi (cos 9)

В это соотношение входят две сферические гармонические функции, которые выражаются через зональную гармоническую функцию Pi(cos0).

В случае диполя мощности ц, находящегося в точке А, согласно п. 15.26 имеем

fxcosa fx (г cos9-с) д 1

~ ~ с2 -2crcos9) ~ (rs-f с2-2crcose)2

Тогда, если г < с, то

cos а / 1 2rPi(cos9) , 3r2P2(cos9) Л

- \ с2 + сЗ с* -Т J

если же г > с, то

= Pi (cos 0) Н- Л (cos 0) + Рз (COS 0) + ... .

Потенциал скорости простого источника (р = т/г представляет собой сферическую гармоническую функцию, как в этом можно непбсредственно убедиться подстановкой в уравнение (2). Если источник расположен в некоторой точке А на оси х на расстоянии с от начала координат (рис. 309), ТОМЫ имеем (f - mIR, где R = AP. Эта функция, являясь потенциалом скорости, должна удовлетворять уравнению Лапласа, как это было установлено в п. 15.20 при рассмотрении уравнения неразрывности. Теперь имеем

= 2 j с2 2сг cos 0 = г2 1 -cos 0 +) = с2 1 - cos 0 +-J )

Если Я, < 1, то имеет место следующее разложение:

(l-2Xcos0 + ?) 2= l+;,p,(cos0)-b?.2p2(cos0)-f

где коэффициенты Pi (cos 0), P2(cos8), ... не зависят от Я,. Положим Я, = г/с, тогда если г < с, то

i = -F + i(°) + -S2(cos0)+....

а если л > с, то

- = -bPi(cos8)-t$P2(cos0)+... .

Поскольку в этих разложениях члены, содержащие г, г^, г',

г', ..., однородны, но имеют разные степени, то, как было отмечено выше, каждый из этих членов представляет собой сферическую гармоническую функцию. Таким образом, мы имеем две последовательности сферических гармонических функций (постоянная с при этом опущена):

1, rPi(cos0), л2р^(соз0),

Pi (cos 9) (cos 9) т- 3 . .

каждая из которых тождественно удовлетворяет уравнению Лапласа. С помощью разложения для бинома легко доказать, что

Pi (cos 0) = cos 0, Рг (cos 8) = Y (3 cos* 9 - 1)

и т. д. функции Pre (cos 8), = 1, 2, 3, ... называются функциями Лежандра, или зональными гармоническими функциями (первого рода). Эти функции встречаются в задачах со сферическими границами. Таким образом, для течения около сферы имеем

Эти соотношения дают потенциал скорости диполя в зависимости от зональных гармонических функций.

Можно сделать следующие дополнительные замечания. Если ф -сферическая гармоническая функция, то все ее частные производные любого порядка по X, у, z также являются гармоническими функциями. Например, d(f/dx является сферической гармонической функцией, как в этом легко убедиться с помощью подстановки в уравнение (1). Так как 1/г представляет собой сферическую гармоническую функцию, то по указанному свойству мы получим также следующие гармонические функции:

jL Х L

гЗ гЗ гЗ

16.12. Теорема Кельвина об инверсии гармонической функции. Если Ф=ф(г, 8, а) - гармоническая функция, то функцижр* = а'1 r[(f{alr, 0, ю)] также является гармонической, причем а -любая постоянная.

Доказательство. Положим R=alr, тогда ф* = ?ф(?, 8, ю). По предположению ф(г, 8, ю) удовлетворяет уравнению Лапласа (2) из п. 16.10, и, следовательно, ф(/?, 8, ю) удовлетворяет аналогичному уравнению, в котором вместо г берется R, а именно уравнению

д 2ф(;?,9, й))л 1 д f д аф {R, е, м) -N i d<(R,Q,a) . WrK, dR у'+ЖеавЛ Ш Ш

и, значит,

а / 2 ЗфЛ 2а* аф (R, 9, ш) , дв di<f(R, 9, ш) а d(R, 9, а) \

дт к! дг J~ Ti dR Т гЗ dRi ay?V dR J

Таким образом,

dr V дт JsinQdQ l aO J + sin 9 aw

,2 Vfsin 8 V ar y+sin9a9 ao y+sin

n r /г.2ф(, e, о)Л 1 a / даф(У?,9, u))-N i а2ф(У?, e, ш)-]

что и требовалось доказать.

Отметим, что точки {г, 8, со) и {alr, 8, со) представляют собой точки, связанные преобразованием инверсии относительно сферы г = а, причем, если одна из них находится внутри сферы, то другая находится вне ее.

16.13. Теорема Вейса для сферы. Для теоремы о круге, доказанной в п. 6.21, имеется аналогичная теорема не только для осесимметричного движения, но и для общего трехмерного движения *).

Теорема Вейса для сферы. Пусть в безграничном пространстве имеется безвихревое течение несжимаемой идеальной жидкости с потенциалом скорости ф {г, 8, со), причем все особые точки этой функции расположены от начала координат на расстоянии, большем чем величина а. Если в область этого течения поместить сферу г=а, то потенциал скорости можно выразить в виде

Ф(г, 8,со) = ф(г, 0,0)) + ! J R.!ldR. (1)

о

Доказательство. Пусть сфера помещена в область течения и пусть теперь потенциал скорости представляется в виде суммы ф(г, 0, со)-{--1-Х(Л 9: ®)i где Х(г, 0, со) - потенциал возмущения, обусловленного

1) Weiss Р., Ргос. Cambr. Phil. Soc, 40 (1945).

сферой. При этом должны быть выполнены следующие условия: должно удовлетворяться уравнение Лапласа, должны отсутствовать возмущения на бесконечности и должна обращаться в нуль нормальная составляющая скорости на сфере. Более точно эти условия выражаются следующим образом: (I) vX = 0, функция X не должна иметь особенностей вне сферы г= а.

(И) Х(л 0, (ii) = o(\ для больших г.

< ) (),=,-°-

Если взять функцию X в виде 5( = - ф (i?, 0, со), где R= alr, то, согласно

п. 16.12, следует, что Vx = 0; кроме того, поскольку все особенности функции ф находятся вне рассматриваемой сферы, то все особенности функции % находятся внутри этой сферы, так как преобразование инверсии отображает внешность сферы на ее внутренность. Итак, условие (I) удовлетворено.

Далее, по предположению, функция ф является регулярной в окрестности начала координат, поэтому она разлагается в ряд вида

Ф(г, 0, а)) = Ло + Л1Г-ЬЛ2/-+...,

где Ло, Ai, Лг не зависят от г. Подставляя этот ряд в выражение для %, легко найдем, что старший член равен

1 , аз

а это показывает, что условие (II) удовлетворено. Чтобы проверить условие (III), вычислим

аФ {т, е, ш)

1 / aN f д^{Я, е, (О)Л

дг дг а \ г' J V dR jRaVr

Эта величина обращается в нуль при г=а, поскольку при этом R=a;

значит, условие (III) также удовлетворено. Итак, теорема доказана.

Заметим, что применение этой теоремы не ограничивается случаем rv осесимметричного движения.

16.20. Концентрические сферы.

Пусть область между твердой сферой радиуса а и концентрической сферической оболочкой внутреннего радиуса b заполнена жидкостью (рис. 310).

К сфере и оболочке приложены некоторые импульсы, приводящие в движение сферу со скоростью U, а оболочку-со скоростью V, направление которой составляет угол а с направлением скорости V. Чтобы рассмотреть движение в начальный момент времени (сферы будут расположены концентрически лишь в начальный момент времени), примем направление U за направление оси х, а начало координат поместим в общем центре этих двух сфер. Тогда граничные условия запишутся в следующем виде: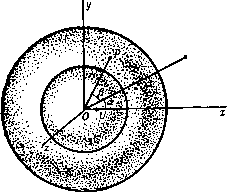

Рис. 310.

=t/cos0 при г=а, 2 = FcosP при г=&,

(1) (2)

где р -угол между направлением V и ОР, причем Р представляет собой точку на оболочке.

Декартовы координаты точки Р равны b cos 0, b sin 0 cos ю, b sin 0 sin со, следовательно, единичный вектор направления OP равен

i cos 0 + j sin 0 cos CO -- к sin 0 sin со.

Если принять, что направление V лежит в плоскости х, у, то единичный вектор направления V равен

icosa + jsina,

где i, j, к -единичные векторы осей х, у, z соответственно.

Скалярное произведение этих векторов, согласно п. 2.11, выражается в виде

cos р = cos а cos 0 + sin а sin 6 cos ® = у cos а + у sin а.

Таким образом, граничное условие (I) показывает, что в функцию ф будут входить гармонические функции х, xlr, а условие (2) показывает, что, кроме того, будут входить и гармонические функции у, у/г^.

Поэтому будем предполагать, что

ср=Ах + §+Су +

или, возвращаясь к полярным координатам, получим Отсюда имеем

Ф= (Аг +-) COS0 + С/--{--) sin0cosco.

дц>

= (-Л-Ь^) cos0 + (-C + )sin0cosco.

Тогда из условий (1) и (2) получим уравнения

(-Л + -) cos0 + (-C-f)sin0cosco = t/cos 0,

(-A + -jcosQ + ( -C + -Jsin0cosco = F (cos а cos 0 + sin a sin 6 cos со).

Эти уравнения должны удовлетворяться при всех значениях 0 и со, и поэтому можно получить следующие уравнения):

-A + =Vcosa, ~C + =Vsma.

Обозначая для краткости с^ = Ь^-а^, находим

D а^бз аЮ-bW cosa В = 2(-<°) =-3-

D=-Vsma, С =

таким образом,

{а^и - bW cos а) г -Ь1 (t/ - V cos а)

1 bV sin а Г , аЗ 1

sin 0 cos CO.

1) Эти уравнения могут быть получены, если последовательно положить 6 равным О и л/2.

Следует подчеркнуть, что этот потенциал скоростей описывает рассматриваемое движение только в начальный момент времени, когда границы расположены концентрически.

16.21. Концентрические сферы, движущиеся в одном направлении.

Если скорости и vi V имеют одинаковое направление, то в формулах п. 16.20 надо положить а = 0, тогда получим

cos i

{aW-bW)r---

Ъ этом случае, когда движение начинается из состояния покоя, величины импульсивных давлений на границах, а именно величины (см. п. 3.64), имеют следующий вид: на внутренней границе

~ acos( СО, =

на внешней границе

~ 6 cos 9 Г ЗаЗ

Импульсивная сила на внутренней границе равна я

/i = J (Dl COS0 sin 0 d0 = у na?Q (a* -Ь(7

Аналогично импульсивная сила на внешней границе равна

, 4 г ЗаЗ

Направления этих сил показаны на рис. 311.

Если изменить направление импульсивных сил /i и /2, то получим импульсивные силы, действующие на жидкость со стороны границ, а их

сумма равна изменению количества движения

жидкости; таким образом, по направлению Ох справедливо равенство

1х-12 = щ {bw - аЮ) = м;у- м;(,

Рис. 311

где Mj и М' соответственно представляют собой массы жидкости, которые могли бы вмещать внутренняя и внешняя границы. Этот результат справедлив не только для сферы, но и для любых двух поверхностей, движущихся произвольным образом. Итак, количество движения жидкости не зависит от плотности внутреннего тела. Следовательно, если представить себе, что внутреннее тело имеет такую же плотность, как и жидкость, то тогда центр массы О этого тела и жидкости будет фиксированным относительно оболочки и будет двигаться со скоростью оболочки V. Поэтому общее количество движения жидкости и внутреннего тела будет равно М'\. Таким образом, количество движения одной только жидкости равно MV -MjU.

Для определения импульса /, требуемого для приведения в движение внутренней сферы, необходимо применить закон количества движения

J-h = MiV,

где Mj -масса сферы.

16.22. Неподвижная внешняя сфера. Если внешняя оболочка находится в покое, т. е. У=0, то тогда

Поэтому, если внешняя граница неподвижна, то присоединенная масса сферы равна

1 263 2аЗ

Эта величина стремится к /zM при 6->со (см. п. 15.32).

Кинетическая энергия жидкости может быть найдена интегрированием или выражена непосредственно через присоединенную массу в следующем виде:

263-2аЗ

Если внешняя оболочка покоится, а внутренняя сфера приводится из состояния покоя в ускоренное движение силой F, создающей ускорение /, то импульс сил за время равен / = F6t, а скорость равна U = fbt, и, следовательно,

16.30. Две сферы, движущиеся вдоль линии центров. Рассмотрим две сферы с центрами в точках А, В я радиусами а, b соответственно; пусть эти сферы движутся одна навстречу другой с соответствующими скоростями и, V (рис. 312).

Рис. 312.

Положение некоторой точки Р в меридиональной плоскости будем определять полярными координатами [г, 8) с полюсом в точке А или полярными координатами (г', 8) с полюсом в точке В. Потенциал скорости ф должен удовлетворять краевым условиям

следовательно, можно записать

Ф = [;ф + Уф2, (1)

л2 2 с2 сЗ

1) Milne-Thomson L. М., Calculus of finite differences, § 11.8.

где каждая из функций ф1 и ф2 удовлетворяет уравнению Лапласа и краевым условиям

Таким образом, функция ф1 есть потенциал скорости для того случая, когда сфера с центром А движется со скоростью, равной единице, по направлению к сфере с центром В, а последняя сфера покоится.

Если бы сфера с центром В отсутствовала, то функция ф1 представляла бы собой потенциал скорости, обусловленный диполем, находящимся в точке Л, ориентированным по направлению АВ и имеющим мощность txo = V2a. Однако наличие сферы с центром В нарушает первое из граничт ных условий (3).

Чтобы удовлетворить этому условию, введем отображение диполя цо относительно сферы с центром В, которое представляет собой диполь мощности (ii, ориентированный вдоль направления ВА и находящийся в точке Ai связанной с точкой Л преобразованием инверсии относительно сферы с центром В. Этот отображенный диполь потребует введения другого отображенного диполя На в точке Л2, связанной с точкой Ai преобразованием инверсии относительно сферы с центром Л и т. д. Таким образом, мы имеем бесконечный ряд отображенных диполей мощности ц^, fX2, цз, ..., находящихся в точках Ai, Л2, Лз, ..., причем нечетные индексы относятся к точкам внутри сферы с центром В, а четные индексы - к точкам внутри сферы с центром Л. Положим fn = AAn. Тогда если обозначить АВ=с, то получим равенства

fi = c--, /2 = 7, /з = с--,..., (4)

tl = Ko(-5), tX2=fil(-(Хз=Ц2(-(-), . (5)

уравнения для функций / сводятся к конечно-разностному уравнению Риккати^), которое в этом случае может быть решено до конца, и тогда можно найти величины х„.

Пользуясь обозначениями, указанными на рис. 312, в результате получаем

хо cos 9 HicosOt , Ц2 cos 92 ,

Ф1 - -+ ri + -Pf-

Это выражение представляет собой точное решение рассматриваемой задачи, но оно имеет неудобную форму.

Для того чтобы получить приближенное решение с точностью до членов с *, заметим, что при отсутствии сферы с центром В потенциал ф1 равен

1 a3cos9 2 г2

Применяя разложение в ряд из п. 16.10 и помещая начало координат в точку В, получим, что вблизи сферы с центром В справедливо равенстве

1 a3cos9 1 аЗ аЗл'Р^ (cos 9) ,

Отсюда нормальная скорость на поверхности сферы с центром В равна

дз cos 6

сЗ

Эту нормальную скорость можно уничтожить, добавляя некоторый член к выражению для функции ф1 в первом приближении; в результате получим второе приближение для функции ф1,

1 аЗсозб , 1 аЗбЗсозе ,сч

ф1=-2-72-+2 1з-Т^. (6)

а нормальная скорость на сфере с центром В обращается теперь в нуль с точностью по крайней мере до членов порядка с . Аналогично с той же точностью получим

1 63 cos 6, 1 аЗбЗсозв ,г,.

ф2 = у-771-+ 7Г-7а- ()

Вблизи сферы с центром А упомянутое выше разложение в ряд имеет вид cos 9 1 2г cos 9 ,

Г'2 - c2 + сЗ +

и, следовательно, при г=а

ф1 = 1асозе, ф2 = 1: + соз0. (8)

Для определения кинетической энергии имеем

причем указанные интегралы берутся по сферам А и В соответственно. Тогда, используя формулы (2) и (3), получаем

7 = 4 Q + (Qi + Q,) UV + P,V4,

Qi=--\dS, д,= 5ф,Ч5в.

По теореме Грина (или путем непосредственного вычисления) получим, что Qi=Q2- Кроме того, А d(pi/dn= -cosQ, dS = 2nasin0 dSna сфере Л и, значит,

cos0sin0de = -. о

Таким образом, с точностью до членов с' имеем и, следовательно,

где Mj и Mg -массы жидкости, вытесненной соответствующими сферами.

16.31. Сфера, движущаяся перпендикулярно стенке. Если в задаче, рассмотренной в п. 16.30, положить V = U и Ь = а, то очевидно, что пло-

где

скость, пересекающая под прямым углом линию АВ в ее середине, будет плоскостью симметрии, через которую не протекает жидкость, (рис. 313). Следовательно, эту плоскость можно заменить бесконечной твердой стенкой, и, таким образом, мы получим случай сферы, движущейся со скоростью и по направлению к стенке. Полагая c = 2h, где /г - расстояние от центра сферы до стенки, запишем выражение для кинетической энергии жидкости в виде

где УИ -масса жидкости, вытесненной сферой.

Сфера при этом движется так, как если бы жидкость была безграничной и в ней двигалась бы еще другая сфера, причем эта другая сфера

является зеркальным отражением первой сферы относительно стенки.

Если сфера движется по направлению к стенке и внешние силы отсутствуют, то полная энергия остается постоянной, т. е.

1(2М + Л1-ь|-)с/2== const.

Рис, 313.

Таким образом, в обоих

Когда сфера приближается к стенке, величина h уменьшается и, следовательно, \/h возрастает. Поэтому скорость и должна уменьшаться, и, значит, сфера отталкивается стенкой. Подобным образом, если скорость сферы направлена от стенки, то с увеличением h величина IJh уменьшается и, значит, скорость U возрастает, случаях сфера отталкивается стенкой. Следовательно, две одинаковые сферы, движущиеся с одной и той же скоростью в противоположном направлении вдоль линии центров, оказывается, будут отталкивать одна другую, когда расстояние между ними будет увеличиваться или уменьшаться. Заметим, что в этом рассуждении речь идет только об относительной скорости, так что сферы могут иметь любые скорости вдоль линии центров. Отмеченное явление уменьшает возможность лобового столкновения между плывущими телами.

16.40. Две сферы, движущиеся под прямыми углами к линии центров.

Если сферы с центрами в Л и S и радиусами а я b движутся соответственно со скоростями и и V, направленными параллельно друг другу и под прямым углом к АВ, то потенциал скорости будет иметь вид (ряс. 314)

Для этого потенциала должны выполняться следующие краевые условия:

Если расстояние с между центрами очень велико, то каждая из этих сфер почти не будет оказывать влияния на другую сферу и для потенци-