для удовлетворения обоим неравенствам необходимо и достаточно, чтобы было D=D*, i)=ij)*.

Доказательство. Пусть Q = ф* - ф, и предположим, что основное течение направлено справа налево, как показано на рис. 306.

На линии у имеем

г|,= 0 и Q = ij)*>0;

на линии Г имеем

1)=1)* и Q = 0.

Согласно принципу максимума, если Й = 0 на у, то Й = О во всей области D. Если Й > О на Y> то Q > О во всей области D.

В точке Р имеем £2 = 0. Следовательно, edQ/dn>0, т. е. q*{P) - -q(P)>0, или q*(P)>q(P).

В точке R имеем Q = 0, следовательно, edQ/dn>0, т. е.

-q*{R)+q{R)0, или q{R)>q*(R).

Это доказывает теорему для плоского или осесимметричного потока, для которого е= 1 или е=\/у, причем обе эти величины положительные. Ясно, что для удовлетворения обоим равенствам мы должны иметь D= D*, ф= ф*.

Если будем удалять Г в бесконечность, так чтобы Q бесконечно увеличивалось, то получим Й = О на Г в каждом ее положении, так что в пределе на бесконечности будем иметь Q = 0.

Второе заключение относительно скорости потока в точке R теряет смысл, а первое остается в виде следующей теоремы.

Теорема сравнения 2. Пусть D и D*- области, занятые двумя плоскими {или осесимметричными) потоками, имеющими одинаковую ненулевую постоянную скорость в бесконечности. Пусть области D и D* ограничены единственными линиями тока у и у*, простирающимися до значений л:=± оо. Если область D является частью области D* и если линии у и у* имеют общую регулярную точку Р, то скорости в точке Р удовлетворяют неравенству

q{P)<q*iP)- (3)

Равенство имеет место только в том случае, если D = D* и оба потока идентичны.

Эти теоремы первоначально были доказаны М. А. Лаврентьевым, а затем в более развернутой форме были даны Гилбаргом^). Теорема сравнения Серрина^).

Пусть Ri и Rz - dee области, занимаемые плоскими или осесимметричными безвихревыми потоками, и пусть Si и S2 -соответствующие линии тока ф=0. Предполагаем, что в каждом потоке ф>0. Пусть Si и S имеют общую дугу MN, так что каждый поток на дуге MN имеет направление от М к N. Далее, предположим, что дуги QM линии Si и NQ линии Sa, имеющие только общую точку Q, вместе с MN ограничивают область

MNQ=.Rs,

внутреннюю относительно Ri и R2. Пусть М и N - регулярные граничные точки и пусть q{M, Ri) - граничная скорость в точке М для потока Ri и аналогично для других точек. Тогда получим

ЖМ, Ri) д(М, R2) ... q{N, Ri) q{N, R2)

1) Gilbarg. J. Rat. Mech. а. Analusis, 1 (1952), 309 - 320. (Л авpe н тьe в М. А Матем. сб., новая серия, 4(46) (1938), № 3 (391-458). -Прим. перев.)

2) Serrin J., Rat. Mech. a. Analysis, 1 (1952), 563 - 572. Теоремы сравнения были применены Серрином и Гилбаргом для доказательства различных теорем единственности для плоских осесимметричвых потоков.

причем знак равенства имеет место тогда и только тогда, когда потоки геометрически подобны.

Доказательство. На рис. 307 изображен тот случай, когда Q находится на конечном расстоянии и в бесконечности.

Если потоки подобны, то в теореме, очевидно, имеет место равенство.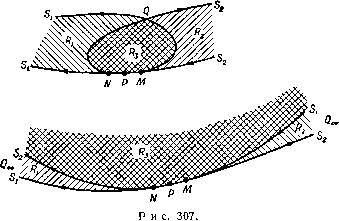

Пусть \pi, фа - соответствующие функции тока и пусть Р точка на линии MN. Пусть

Qp = q (Р, Ri) Фа - (Р, R) Ь- (5)

На QM

Qp=q(P, /?1)фа>0;

на MN

Qp = 0;

на NQ

Qp= -q{P, /?2)ф1<0. Если dn -элемент нормали в точке Р, проведенный в сторону потока, то

в^=,(Р, Ri).-q(P,R,),

= q{P, Ri)q(P, R2)-qiP, R2)q(P, Ri)=0.

Таким образом, линия Cp начинается в точке Р, в которой fip= О (рис. 308).

Рассмотрим область D, ограниченную линиями QM, МР, Ср. На QM имеем

Йр>0; Qp = 0,

Согласно принципу максимума, либо Qp = 0 в области D, либо > О в области D. Должно иметь место последнее условие. Следовательно, (edQp/dn)M>0, т. е.

q (Р, Ri) q (М, R,) - q (Р, R) q {М, R) > 0. (6)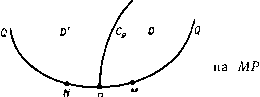

Точно так же в области D, ограниченной линиями Ср, PN, NQ, находим, что Йр < О и {д^р/дп) < О или

q {?, Ri)q (N, R) - q (P, R2) q {N, Ri) < 0. (7)

Из неравенств (6) и (7) немедленно следует утверждение теоремы.

Мы предлагаем читателю доказать, что плоская линия Ср проходит через точку Q.

ПРИМЕРЫ К ГЛАВЕ 15

1. Построить графически в трех измерениях линии тока для источника и равного по мощности стока.

2. Источник мощности т помещен в начале координат в поток несжимаемой жидкости, движущейся со скоростью U в отрицательном направлении оси х. Найти уравнение поверхности равного давления и начертить схематически вид меридионального сечения

трех таких поверхностей, соответствующих р = ро, где ро-давление в бесконечности.

В случае р=ро-гех* и х*< -5-1/ доказать, что плоскость х^Ахт} l*-U касается

о

поверхности постоянного давления по окружности, и найти радиус этой окружности.

3. Если АВ-постоянной мощности линейный источник и А, В - равные стоки такой мощности, что нет ни притока, ни потери жидкости, то показать, что

где с=АВ, Л1 и Л2-соответственно расстояния от точек А, В; С-константа, зависящая от мощностей источников.

4. Два источника мощностей т, т' помещены соответственно в двух точках А, В в бесконечном потоке, текущем со скоростью V параллельно АВ. Получить уравнения линий тока в форме

mcose+m cosG -Уш2/2=соп51,

где (г, 6), (/, 9) -биполярные координаты с точками А я В ъ качестве полюсов; АВ называется начальной линией, ш-расстояние по перпендикуляру какой-либо точки от линии ЛВ.

Показать, что основной поток,поток, вытекающий из точки А, поток, вытекающий из точки В, разделяются геометрическими кривыми, определяемыми уравнениями

т

и

m/(.cos)Vm7(sin-)=V.

5. Пусть в точках А и В бесконечной жидкости находятся соответственно простой источник и сток мощностей х и ц'. Показать, что уравнение линий тока имеет вид

ц cos 9-ц' cos 9 = const,

где 9, 9 -углы, которые отрезки АР, BP образуют с линией АВ, причем Р -любая точка.

Также доказать, что если Ц>ц', то конус, определяемый уравнением

cos9=l -2ц7ц,

делит линии тока, выходящие из точки А, на две серии, одна из которых распространяется до бесконечности, а другая заканчивается в В.

6. Доказать, что если О, Ci, С2-точки на оси х, так что OCi = Ci, ОС2 = С2 и qc2 = a2, то функция тока

ф = т

Л2-л а(х-С2) , X-Cj

а С1Л2 Л1 J

дает движение жидкости, обусловленное простым источником мощности m в Ci при наличии неподвижной сферы радиуса л=а, где л, /-j, /-j -расстояния какой-либо точки соответственно от точек О, Ci, С2, О-начало координат.

15, Масса жидкости плотности q и объема 4ясЗ/3 имеет форму сферического слоя. К внешней поверхности слоя приложено постоянное давление pq. К внутренней поверхио-

7. Найти выражение потенциала скоростей, обусловленного непрерывным распределением источников и стоков вдоль оси x в идеальной жидкости. Если распределение имеет постоянную интенсивность s от точки x-q до точки х-а, то показать, что эквипотенциальные поверхности являются эллипсоидами вращения с фокусами на двух концах линии.

Если в дополнение к вышеуказанному имеется сток равной мощности в начале координат и установившийся поток со скоростью I в бесконечности, параллельный оси х, то показать, что имеется замкнутая поверхность вращения вида дирижабля, полная длина которой является разностью корней уравнения

д;3±л;2а=5а2/(4яК).

8. Интерпретировать движения, для которых функции тока равны

(I) f=:CS2(-l),

где г п г' измеряются от двух фиксированных точек О, О' на оси Ох.

9. Если в начале координат имеется диполь с моментом i в направлении единичного вектора ai, то доказать, что его потенциал скоростей имеет вид

9 = H(aiV)(l,

где г-радиус-вектор точки, в которой вычисляется ф. Истолковать выражение

f.iH2(aiV) (biV)(-l-

10. Определить функцию тока ф, если скорость выражается в виде

11. Доказать, что выражение

f=(-cose-fВл2 sine

представляет собой возможную форму функции тока Стокса и найти соответствующий потенциал скоростей.

12. Сферическая масса жидкости радиуса Ь и плотности Q имеет концентрическую сферическую каверну радиуса а, которая содержит газ при давлении р, массой которого можно пренебречь. Жидкость находилась в покое, когда к внешней границе было приложено импульсивное давление ш.

Показать, что созданная при этом кинетическая энергия равна

2яш2аб/р(ь а).

Если во время последующего движения газ подчиняется закону Бойля н давление на внешнюю границу отсутствует, то найти радиус каверны, когда жидкость успокоится.

13. Масса жидкости плотности Q ограничена двумя концентрическими сферическими поверхностями радиусов ri и г^, и когда жидкость покоится, к этим поверхностям прикладываются импульсивные давления щ и а^. Показать, что поверхности начинают двигаться со скоростями

0)1-0)2 2 Si -0)2 fj

14. Масса жидкости плотности q и объема 4ясЗ/3 имеет форму сферического слоя. К внешней поверхности приложено давление р, а на внутренней поверхности давление равно нулю. Первоначально жидкость покоится и внешний радиус равен 2пс. Показать, что если внешний радиус становится равным пс, то скорость U внешней поверхности дается формулой

j,14p ( з-1)з

1/2аЗ

Р=Ро-Q-27r

[0+)-(-)]

Далее, показать, что если V превышает величину VSpo/Q, то в жидкости образуется полое кольцо вокруг экватора сферы.

23. Сфера радиуса а движется в бесконечной жидкости с переменной скоростью V в направлении оси х. Показать, что давление на поверхности сферы оказывается наименьшим над малым кругом

2а2 dV X--QY2 dt

причем центр сферы находится в начале координат.

24. Получить решение для безвихревого движения несжимаемой жидкости, в которой сфера радиуса а движется со скоростью U. Найти уравнение линий тока в этом

сти не прикладывается никакое давление и никакие другие силы не действуют на жидкость. Первоначально жидкость покоится и внутренний радиус слоя равен 2с. Доказать, что если радиус внутренней поверхности равен с, то ее скорость равна

/14ро 2Уз

16. Бесконечная масса жидкости, находящаяся в покое, подвергается действию постоянного давления ро и содержит сферическую каверну радиуса а, наполненную газом, находящимся под давлением тро- Доказать, что если пренебречь инерцией газа и предположить, что во все время движения справедлив закон Бойля, то радиус сферы колеблется между а и па, где величина п определяется уравнением

1-ЬЗт1п -и3=0.

Если Q-плотность жидкости, а величина т приблизительно равна единице, то показать, что период колебания равен 2я (а^д/ (Зро)).

17. Некоторое количество жидкости, частицы которой взаимно притягиваются согласно закону гравитации, окружает твердую сферу радиуса а, причем радиус внешней свободной поверхности равен Ь. Твердая сфера внезапно уничтожается. Показать, что если радиус внутренней поверхности равен г, то квадрат скорости в каждой точке равен

й/? [3 (rS-aS)-5 (лЗ/?2 аЗб2) 2 (j?8-Ь )] rHR~r)

где i?3 = r3-f-b3 a3 и k - константа.

18. Пусть некоторый объем жидкости, находящийся под действием гравитации, первоначально покоится, имея форму сферического слоя очень большого радиуса, и сжимается под действием собственного притяжения, причем ни на какую поверхность слоя не оказывается никакого давления. Доказать, что если внутренний радиус равен х, то справедливо уравнение

/dx \2 AitvQ

С 5Г j = У(.У--х}(ЗхЗ+6х>у+4ху-{.2у!>).

где £/3 = л:3--сЗ, Y -постоянная притяжения, а §-плотность; 4ясЗ/3-объем жидкости.

19. Сфера движется по прямой линии со скоростью U. Найти действующую силу путем непосредственного вычисления результирующего давления жидкости.

20. Сфера брошена и падает под действием силы тяжести со скоростью U под углом 45° к горизонту. Если плотность сферы равна удвоенной плотности жидкости, то доказать, что наибольшая высота над точкой бросания, достигаемая сферой, равна 5i/2/(8g).

21. Сфера радиуса а помещена в бесконечный поток жидкости, текущей с постоянной скоростью V. Показать, что линии тока задаются уравнением

(аЗ-r3)sin2e/r=const.

Если сферу разделить на две части диаметральной плоскостью, перпендикулярной направлению движения потока, то показать, что результирующая сила между двумя частями меньше, чем в случае, если бы жидкость покоилась, причем давление в бесконечности остается тем же и равным пда^У^/16.

22. Сфера радиуса а движется с постоянной скоростью V в безграничной жидкости, покоящейся в бесконечности. Если ро-давление в бесконечности, то доказать, что давление р в любой точке Р, находящейся на расстоянии г от центра сферы О, причем ОР образует угол 9 с направлением скорости сферы, дается формулой

2sin2e(l-) = 62,

где Ь-константа, зависящая от частицы.

Объяснить, почему это уравнение не тождественно с уравнением линии тока, и показать, что положение частицы на ее траектории выражается в зависимости от времени уравнением

-1/2

-U0-)(--)

25. Сфера радиуса а движется с постоянной скоростью V в бесконечной жидкости. Найти потенциал скорости и показать, что уравнение траектории частицы получается посредством исключения л, 9 из уравнений

X = rCQS

А(лЗ аЗ)(лЗ-аЗ-/-сЗ) y=rsinQ, /-3-аЗ = /-с2 cosece,

где с-произвольная постоянная.

26. Сфера радиуса а является неподвижной в жидкости, которая обтекает ее таким образом, что на большом расстоянии от сферы скорость постоянна. Окрашенную частицу жидкости поместили выше по потоку в точке, лежащей на оси системы, и наблюдают за движением этой частицы. Если, в то время как частица находится выше по течению, ее расстояние от центра изменяется за время Т от Zi до Z2, то показать, что максимальная скорость жидкости на сфере равна

3 2Т

Г £ (z?-a3) (z2-a)3 £ a,(Zi-Z2)K3

Lzi-Z2- g 1П(зЗ дЗ)(2 а)з tg2(ziZ2+a2)+a(zi+Z2) .

27. Поток воды на большой глубине вдоль плоского горизонтального дна имеет постоянную скорость V. Полусфера весом w радиуса а расположена основанием на дне. Доказать, что средняя величина давления между основанием полусферы и дном меньше, чем давление жидкости в каждой точке дна на большом расстоянии от полусферы, если

28. Однородная полупогруженная сфера массы М плавает в горизонтальных направлениях в безграничной бесконечно глубокой жидкости под действием силы тяжести. Если сфера внезапно начинает двигаться со скоростью U, направленной вертикально вниз, то показать, что требуемый импульс равен 3MU/2. Доказать, что направленная вверх скорость жидкости, находящейся в соприкосновении со сферой на свободной поверхности, равна 0,5 U.

29. Сфера радиуса а движется с постоянной скоростью U в бесконечной жидкости, покоящейся в бесконечности. Если ро-давление в бесконечности, то показать, что давление р в каждой точке поверхности сферы, радиус которой образует угол 6 с направлением движения, выражается формулой

Если сферу разделить на две полусферы плоскостью, наклоненной по углом а к направлению движения, то показать, что нормальная и тангенциальная компоненты сил, действующих между двумя полусферами и обусловленных давлением жидкости, равны соответственно

(И -9sin2a) Po-QU--32--

-jg- ngaW sin a cos a.

30. Если два диполя с моментами fi, ц' имеют общую ось, то показать, что один из слоев потока представляет собой сферу.

31. Найти функцию тока для диполя в точке О, находящейся внутри неподвижной сферы радиуса а, центр которой находится на оси двойного источника на расстояний, с от точки О. Рассчитать в этом случае давление в каждой точке сферы.

движении и доказать, что уравнение траектории частицы относительно центра движущейся сферы имеет вид

где нормальная скорость около элемента dS поверхности сферы; интеграл берется по поверхности сферы.

33. Если диполь S помещен вблизи неподвижной сферы радиуса а с центром О, находящимся на расстоянии с от S, то найти функцию тока и показать, что скорость в точке Р на поверхности сферы равна

{Зт(с2-a2)sine}/r5,

фере имеет результир 24т2ела8с/(с2-а2)4,

где r = SP и в-угол SOP.

Доказать, что давление на сфере имеет результирующую силу

направленную к диполю.

34. Определить отображение диполя относительно сферы, ось которого проходит через центр сферы.

Доказать, что если расстояние диполя от центра велико по сравнению с радиусом, то результирующее давление на сферу приближенно пропорционально обратной величине седьмой степени расстояния.

35. Диполь с моментом х помещен в центре неподвижной полой сферы радиуса а, которая наполнена несжимаемой невязкой жидкостью. Показать, как получить давление в любой точке, задавая давление ро в точке А сферы, которая лежит на оси диполя, и показать, что уравнение одной из поверхностей равного давления имеет вид

(r/a)s=(l+itg2 9)/(2- tg2 9).

36. Твердое тело ограничено внешней частью двух равных сфер радиуса а, которые пересекаются ортогонально и окружены неограниченной жидкостью. Если твердое тело приведено в движение со скоростью и в направлении линии центров, то показать, что потенциал скоростей результирующего движения равен

1 , /cos 9 . cos 9 cose Л

где г, г', У?-радиусы-векторы, отсчитываемые соответственно от центров двух сфер и точки, расположенной посредине между ними; 6, 6, в-углы, которые образуют эти радиусы-векторы с направлением движения твердого тела.

37. Найти потенциал скоростей, обусловленный простым источником, находящимся вне неподвижной сферы в неограниченной невязкой жидкости.

Доказать, что сфера притягивается по направлению к источнику; доказать также, что если радиус мал по сравнению с расстоянием до источника, то притяжение в первом приближении, обратно пропорционально пятой степени расстояния.

38. Доказать, что потенциал скоростей, обусловленный отображением источника мощности m относительно сферы радиуса а, равен потенциалу, обусловленному распределением диполей по поверхности сферы, причем оси перпендикулярны к поверхности, и момент, приходящийся на единицу площади, равен

где с-расстояние источника от центра и У?-расстояние от точки инверсии.

32. Диполь с единичным моментом и осью, параллельной оси х, помещен в точке (О, О, с) вне неподвижной сферы радиуса а с центром в начале координат и погруженной в неограниченную жидкость. Доказать, что вблизи сферы потенциал скоростей Ф, обусловленный диполем и его отображением, равен

где г, 9, ф-сферические координаты, (x = cos9, а P i (fx)-зональные поверхностные гармоники степени (п-1). При доказательстве можно использовать соотношение

Показать, что компонента скорости жидкости вдоль оси х в точке (О, О, с), обусловленная сферой, движущейся с данной скоростью (при отсутствии диполя), равна

а r-R

cosG-f-- cosG-f ---

дает движение, обусловленное простым источником S мощности fx, помещенным на расстояние с от центра неподвижной сферы радиуса а, причем R отсчитывается от центра сферы, {г, в) отсчитываются от S и (г', 9) - от инверсии точки S относительно сферы.

41. Источник и сток равных мощностей помещены в точках (О, О, -с) внутри сферы радиуса а с центром в точке (О, О, 0). Найти выражение для потенциала скоростей в точках внутри сферы.

42. Найти отображение источника относительно сферы; О-центр, Р, Q-точки вне сферы на одном и том же радиусе, причем точка Q расположена ближе к сфере, и Р', Q - точки инверсии для Р, Q. Доказать что источник мощности fx в точке Q и источник мощности fxa/OQ в точке Q создают такой же радиальный поток в каждой части поверхности сферы как и линейный источник, равномерно распределенный вдоль отрезка QP полной мощности fi, вместе с линейным источником, равномерно распределенным вдоль отрезка PQ мощности fxa/OQ.

43. Твердая сфера радиуса а колеблется в бесконечной жидкости по простому гармоническому закону ccosp, где с-малая величина. Определить направление и величину результирующего колебания в любой точке жидкости.

44. Центр сферы радиуса а, находящейся в неограниченной жидкости, совершает малые линейные колебания, причем перемещение за время t равно csinn Доказать, что средняя кинетическая энергия, приходящаяся на единицу объема жидкости в точке (т, G), равна

btX (+3cos29).

Причем полюс находится в центре сферы, полярная ось совпадает с линией движения сферы.

Рассчитать периодическую силу, необходимую для поддержания движения.

45. Сфера переменного радиуса а движется в бесконечной жидкости с переменной скоростью V в указанном направлении. Найти давление в любой точке поверхности сферы и показать, что результирующее давление жидкости на сферу равно

46. Жидкость, простирающаяся до бесконечности, окружает сферическую границу, радиус которой в момент времени t равен {а-\-Ь smnt), причем центр ее неподвижен. Если внешние силы отсутствуют, то показать, что давление на границу равно

Ро--- Qbn (56 cos 2nt-4а sin nt-\-b),

где Ро-давление в бесконечности.

47. Сфера радиуса а, окруженная бесконечной жидкостью, покоящейся на очень большом расстоянии от сферы, находится под давлением Ро- Если сфера вибрирует радиально, так что радиус в любой момент времени равен {а-\-Ь cos nt) и массовые силы отсутствуют, то найти давление на поверхность сферы в любой момент времени и показать, что его наименьшее значение равно

Ро-пЦЬ (а-\-Ь).

48. Показать, что движение, возникающее от импульсивного давления, приложенного к границе жидкости, безвихревое.

Сферический пузырь пара в большой массе воды плотности q при отсутствии массовых сил внезапно практически теряет все свое внутреннее давление при конденсации

39. Источник мощности т расположен в жидкости, ограниченной изнутри неподвижной сферой радиуса а, на расстоянии с от центра сферы. Доказать, что потенциал скоростей в точке на поверхности равен

2ffl ffl г-j-c-f-g

г а г-{-с-а

где г-расстояние точки от источника.

Найти величину скорости в каждой точке на поверхности.

40. Определить функцию тока Стокса для движения несжимаемой жидкости, симметричной относительно оси; показать, что возможными функциями Стокса являются следующие функцрги: г-г' и cosO; где г=ОР, г' = 0Р, Ь = РОО', причем 00 -две любые неподвижные точки на оси симметрии. Интерпретировать эти функции.

Доказать, что функция тока

пара. Если в этот момент радиус пузыря равен а, то показать, что пузырь лопается в момент времени

бро

где Ро-давление на большом расстоянии.

49. Бесконечная масса жидкости наполняет область вне неподвижной сферы радиуса а и притягивается к центру сферы^с силой ц/л*, приходящейся на единицу массы. Если давление в бесконечности равно ш и сфера внезапно исчезает, то показать, что мгновенное изменение давления на расстоянии г равно (а)а-\-цд)/г.

Найти скорость внутренней границы жидкости в каждый последующий момент времени. В частном случае, когда давление в бесконечности равно нулю, найти время, необходимое для того, чтобы полость целиком заполнилась жидкостью.

50. Бесконечная покоящаяся жидкость постоянной плотности q, находящаяся под постоянным давлением Р, содержит сферический пузырь радиуса оо, наполненный паром, который несет электрический заряд в, равномерно распределенный по поверхности. Предположим, что этот заряд всегда остается одним и тем же и производит направленное наружу давление на единицу площади поверхности, равное е^/вяа*, где а-радиус пузыря. Предположим также, что пар внезапно конденсируется, причем внутреннее давление падает до нуля. Найти давление на расстоянии г от центра пузыря, если его радиус равен а, и доказать, что тогда

Получить из этого равенства, что если 3e/8naoP = cil-\-alao-haiao, то радиус пузыря будет колебаться между пределами Oq и щ, и найти формулу для периода.

51. Получить дифференциальное уравнение поверхности, которая во все время движения состоит из одних и тех же частиц жидкости.

В момент времени t = 0 сферический пузырь газа радиуса а покоится внутри окружающей его большой массы тяжелой жидкости плотности Q, которая также покоится. Давление газа равно ро, а давление жидкости в горизонтальной плоскости, проходящей через центр пузыря, равно р. Доказать, что в начальном движении радиус пузыря начинает расти с ускорением {Ро-рЖоа), причем центр пузыря начинает двигаться вверх с ускорением 1g, и пузырь приближенно остается сферическим, если прн этом пренебрегать инерцией газа и поверхностным натяжением.

52. Уравнение меридионального сечения поверхности вращения имеет вид г =

= asec-2-6, где 0<е<л. Поверхность помещена в равномерный поток, движущийся со скоростью и. Показать, что функция тока имеет вид

и

-irasinae -a2(i cose) ,

и найти потенциал скоростей.

53. Легкий тонкий круглый диск радиуса с покоится на поверхности неподвижной жидкости плотности Q, бесконечной протяженности и глубины. К центру диска приложен вертикальный, направленный вниз импульс /. Показать, что скорость, сообщенная диску, равна 3 (4есЗ).

54. Сфероидальные координаты , ц, ш получаются из цилиндрических координат ш, X, ш посредством преобразований

a-\-ix = k&m (O-j-iri),

= shAri, fx=cose.

Получить в этих координатах уравнение Лапласа вида

Найти в этих координатах граничные условия, если сплющенный сфероид движется вдоль своей оси со скоростью U в неограниченной покоящейся жидкости.

55. Воздушный корабль в форме вытянутого сфероида с полярной полуосью а и экваториальной полуосью Ь движется со скоростью U параллельно своей оси вращения в воздухе, который можно рассматривать как несжимаемую жидкость. Найти выражение Для потенциала скоростей в каждой точке жидкости, а также для давления в каж-

2 sha cha-а

где М'-масса вытесненной жидкости,

58. Показать, что в сферических координатах {ц, , со), определяемых уравнениями

x = a\iZ у=а)С05Ш, z=<Bsino),

S=a(l-n2)V*(C2+l)V2

уравнение неразрывности имеет вид д

2 au)2

Если тонкий круглый диск радиуса а движется со скоростью U параллельно своей оси в бесконечной массе жидкости, то доказать, что потенциал скоростей равен

= (2aU/n) II {\-lavcctg О, 4

и показать, что кинетическая энергия жидкости равна ураз/уг.

59. Полость между двумя параболоидами х^-\-у^=а2, x-\-y = b{z-c) (где а, Ь, с-положительны и 6>а) заполнена покоящейся жидкостью. Внезапно граничные поверхности начинают двигаться соответственно со скоростями U, V в направлении оси г. Доказать, что образующиеся при движении поверхности, на которых функция тока постоянна, являются параболоидами с фокальным параметром аЬ (U-V)/(aU - bV).

60. Если <в--1лг = /(l-j-tT)), то показать, что уравнение

имеет решение типа ф = ш*17К, где U, К-соответственно функции координат (, т)) при условии, что

(f)+(f) = - >+4-

Если (-j- Ti) (ш--1г) = а, то показать, что имеется решение вида Ф = и^+г1)-в± У1(/гл).

дой точке оболочки воздушного корабля при условии, что давление в бесконечности равно Яо.

56. Доказать, что если сфероидальный диск, в котором а = 6= 100с, движется по воде со скоростью 0,3 м/сек в направлении своей наименьшей оси, то скорость у края равна приближенно 19,2 м/сек.

57. Получить формулу

для кинетической энергии жидкости, находящейся в области, ограниченной изнутри движущейся поверхностью S и покоящейся в бесконечности; причем нормаль п проведена внутрь жидкости.

Доказать, что если S -вытянутый сфероид с эксцентриситетом, равным tha, движущийся параллельно своей оси симметрии со скоростью V, то кинетическая энергия жидкости равна

ImV a-tha