Поэтому из формулы (1) находим

ф= m + mcos6i -(/- - 2) + cos02.

Последние два члена дают отображение источника относительно сферы, которое, таким образом, состоит из источника мощности ma/f в точке инверсии и линейного стока мощности т/а на единицу длины, распределенного на отрезке от точки инверсии до центра.

15.41. Отображение радиального диполя относительно сферы. Рассмотрим диполь с моментом ц, помещенный в точке А на радиусе а сферы с центром О. Примем OA в качестве оси момента ц. Тогда при использовании диаграммы и обозначений п. 15.40 функция тока, обусловленная только диполем с моментом fi, запишется в виде фо= - и sin 8i -i = = - ix (1 - cosOi) -!. По теореме Бутлера для сферы радиуса а мы имеем

sinei iir\-PM/PO (i£in2 ei jxOA12 Ho DM = / sin 62 = (O/f) sin 62- Следовательно,

Таким образом, ось требуемого отображения направлена противоположно оси диполя с моментом ца/f, и отображение расположено в точке инверсии (см. п. 8.81).

15.42. Сила, действующая на препятствие. Пусть имеется установившееся безвихревое движение жидкости. Пусть, кроме того, имеется п особенностей потока, каждая из которых находится на конечном расстоянии от препятствия. Пусть 5о - поверхность, ограничивающая препятствие, и пусть 5; (/=1, 2, ..., га) - сферы бесконечно малого радиуса, каждая из которых окружает одну особенность. Пусть S +i -сфера большого радиуса, окружающая сферы 5г(/ = 0, 1, 2, га), и пусть через V обозначен объем сферы, внешней относительно сфер St, но внутренней относительно сферы Sn+i. Тогда по теореме Гаусса находим

2 5 [nq - 2q (nq)] d5 = - J [V? - 2q (Vq) - 2 (qV) q] dx =

i=0 (Sj) (V)

= [2qX(VXq)-2q(Vq)]dT = 0,

так как Vq = 0 и VXq=0, то получим

2 \ [nq~2q{nq)]dS=- [n-2q(nq)] d5.

Интеграл, стоящий в левой части этого соотношения, не зависит от сферы Sn+i, следовательно, это относится также к интегралу, стоящему справа, и если q = 0{l/R), то ясно, что подинтегральное выражение интеграла, стоящего справа, имеет порядок 0{l/R) и, значит, оно должно стремиться к нулю при R->co. Таким образом, интеграл тождественно равен нулю, и, следовательно, положив

и= -nq + q{nq), (1)

4Kmpq

Р и с. 302.

Si, то для точек, находящихся на поверхности этой сферы, мы можем' написать равенство

q = 7i-+qb

где ф -скорость в точке Гг, обусловленная всеми причинами, кроме имеющейся там особенности. Подставляя эту величину в формулу (5) и учитывая, что ndS = 0 по замкнутой поверхности, получим

Fi = AnmiQC\i, Li = riX 4nmiQqi. (6)

Эти формулы показывают, что в случае источника мы можем считать, что действие жидкости на препятствие обусловлено просто силой Р;, действующей в г-м источнике (/=1, 2, ..., ).

МЫ будем иметь

п

- J ud5 = 2 \ udS. (2)

(So) г=1 (S.)

Точно таким же образом докажем, что

- 5 rxud5=2 J rXud5. (3)

(So) (Si)

Таким образом, если f, l обозначают силу и момент силы, действующей на препятствие, то из п. 3.62 видно, что

п п

f=2q ud5, l=2 5 х - (4)

i=l (S;) i=l (S;)

Следовательно, действие жидкости на препятствие можно рассматривать как результат действия системы сил и моментов (рис. 302)

Fi = Q ndS, Lt=Q J rXudS. (5)

(Si) Фг)

Предположим, что i-я особенность является источником мощности Ши расположенным в точке г,-. Тогда если г -радиус бесконечно малой сферы,

Для нахождения действия диполя рассмотрим сток - m в точке А и

источник т в точке В, где АВ = г\.

Если q -скорость в стоке, обусловленная всеми причинами, за исключением действия источника и стока, то скорость в источнике, обусловленная всеми причинами, за исключением источника, равна

q+=q+( V)q-mтl/1l

в то время как скорость в стоке, обусловленная всеми причинами, за исключением стока, равна

q = q - тц/rf.

Следовательно, из формул (6) получаем, что в источнике действует сила Anmqq, а в стоке -сила - 4nmQq . Силы, действующие вдоль линии АВ, сокращаются и остаются силы, указанные на рис. 302. В пределе, если мы имеем диполь с моментом р.= т]т, то в результате получаем силу и пару сил

F=4nQ(fiV)q, L=4nQiiiXq, (7)

где q -скорость, обусловленная диполем.

15.43. Действие источника на сферу. Из п. 15.40 находим, что система, отображающая источник т, находящийся на расстоянии / от центра сферы радиуса а, вызывает радиальную скорость maf~(P - a)~, и, следовательно, сфера притягивается по направлению к источнику силой

15.44. Действие радиального диполя на сферу. Из п. 15.41 находим, что скорость, обусловленная отображенным диполем в точке {г, 6), равна

2ц, cos 9 aS

причем полюсом координат является инверсия положения диполя. Согласно формуле (7) п. 15.42, сфера притягивается по направлению к диполю силой

Г а / 2icose аЗ 24яд|хааЗ/

15.50. Уравнение для функции тока при безвихревом движении. Если поток симметричен относительно оси х, то, согласно формуле (8) п. 2.72, вихрь равен

9- дд

(л

Iw дх \ oi J дш \(й да J sinco V w У

дх да

При безвихревом движении имеем

ал: V 0) дх J аш V со aw /

что представляет собой искомое уравнение.

Теперь покажем, что конформное отображение

г^ = х + й=!{1 + щ) = 1{1)

dt,\m dl

обращается в нуль, а она и представляет собой левую часть уравнения (2). 15.51. Скорость. Мы имеем

и, следовательно.

п^4->п 1 i d I d

4 af af 2 dZi ai

Тогда конформное преобразование Zi = / (2) дает

S2 azi ag azi dl

И, следовательно,

,wr®7(&=4ff=(f)%(*).

Если через ds и ds обозначить элементы дуг, соответствующих увеличению значений и то мы получим

(dsj)2 -f (ds,)2 = (ds)2 = (d)2 4- (dm) = / (S) 7 (I) =

где P {t,)f {Q. Таким образом, компоненты скорости в направлениях увеличения значений , г| выражаются формулами

аф 1 аф 1 аф

1) аметим, что f можно рассматривать как функцию независимых переменных z, Zi, или Si. Таким образом, Z, есть функция только от Zj, и, следовательно, функция только от Zi.

преобразует вышеуказанное уравнение в следующее:

где величина m рассматривается как функция переменных , г|, определяемая конформным отображением. Доказательство. Так как

то мы видим ), что уравнение (1) эквивалентно обращению в нуль действительной части выражения

dzi \a dzi J V, ш dl, J dzi V S ag У dz dzi ag V ш dt, J

Первые два множителя, стоящие в правой части, являются сопряженными мнимыми величинами, произведение которых действительно, и, следовательно, действительная часть выражения

а

или через функцию тока 1 аф

/5 дц

1 Ф 1 Ф т ds ~ /ш ag

Из этих результатов получаем уравнения (см. п. 5.30) аф 1 аф аф i аф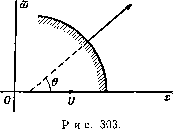

15.52. Граничные условия для функции тока. Если твердое тело вращения движется в жидкости со скоростью и в направлении своей оси, то скорость, нормальная к твердому телу, и нормальная скорость соприкасающейся с телом жидкости являются одинаковыми (рис. 303). Тогда

0) as ds

интегрируя вдоль границы, получим

ф= - у (/oa+const.

Если жидкость покоится в бесконечности, то присутствие твердого тела не будет оказывать никакого влияния на жидкость в бесконечности, поэтому функция тока ф должна стремиться на бесконечности к постоянному значению. Без потери общности константу можно положить равной нулю.

15.53. Сфера. Одним из простейших примеров применения вышеуказанных результатов является движение сферы. Преобразование

дает х= сесозц, а =cesmr\, так что поверхности = const являются сферами. Для сферы радиуса а мы имеем а = се. Уравнение, которому удовлетворяет функция тока, таково:

( афл а 1 5ФЛ о

VesinTi dlJ дц \ ьтц ц J

e*sinTi d\ J дц \е^ь\х\.ц Ц

Если сфера движется со скоростью V в направлении оси х, то на поверхности имеет место равенство

ф=--f/cVosinr, (2)

а в бесконечности, где жидкость не возмущена, имеем

Решение уравнения ищем в виде ф =/() sinri. Тогда, подставляя это выражение в уравнение (1) и интегрируя, получаем

[e-lf(g)]-2e-l/() = 0,

Г (Ю - / (I) - 2/ (I) = 0. / (I) = + Се-\ Из формулы (3) следует, что В = 0, и тогда из равенства (2) следует

откуда находим

1э= -ycWbsm2r/el= --i a f/sin б/г, что уже было получено в п. 15.32.

15.54. Функция тока для сжатого эллипсоида. Сжатый (или дискообразный) эллипсоид представляет собой тело, полученное вращением эллипса относительно его малой оси. Это тело известно также как сплющенный

у полюсов сфероид. Приблизительно эту форму имеют планеты Земля и Юпитер. Преобразование

2i = х:-1-гш= с sh 2 (1)

дает x = cshCOST], (о= cch i sinr], и, следовательно, кривая I = о является эллипсом в меридиональной плоскости с полуосями

a = ccho, 6 = csho-

Таким образом, § = So представляет собой уравнение эллипсоида (рис. 304).

Функция тока удовлетворяет уравнению (см. п. 15.50)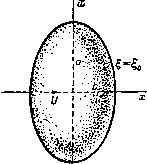

Рис. 304.

af \

= 0.

ag V.ch§sinTi ag J ari Vchgsimi dr\ J

Если эллипсоид движется со скоростью II в жидкости, которая покоится в бесконечности, то функция ф должна удовлетворять следующим условиям:

ф= -(/chiosinri

на твердой поверхности и

ф->0

в бесконечности.

Условие (3) указывает, что решение должно иметь вид ф= / () sinT]. Подстановка в уравнение (2) и интегрирование дают

/ (l)ch§-/(l)sh()-2/(g)chg = 0, /(g)chg-2/()sh = B,

f{l)=Bc\i4\

ch3

где В и С -константы, причем из условия (4) следует, что С=0.

Теперь с помощью интегрирования по частям или непосредственной проверкой находим

здесь мы полагаем D=0, так как другие члены стремятся к нулю при > со. Таким образом, имеем

/()=-i5chn(-arcctgshg) .

Чтобы доказать, что /()->0 при - оо, заметим, что для больших значений i

I - ch4 arcctg sh I = sh I - =0.

Таким образом, условие (4) удовлетворяется.

Для определения постоянного В из (3) находим

В ch о -arcctg sh lo) = -i/c4h4o.

a=cchlo, b= aY I -= с shlo.

Следовательно,

B=~Ucl{ey\-e - arcsine).

Таким образом, окончательно мы получим следующее выражение для функции тока:

-4- i/c2 (sh I-ch2 garcctgsh ф=--у=-sinri. (5)

e/l-e2 arcsin e

Для определения потенциала скорости из п. 15.51 находим

1 (Эф

Зг1 ~ с ch I sin Г] д\

Следовательно, из формулы (5) получим

= l(2-2shiarcctgsh)5mTi. k

с * е ]/l-e2-arcsinе

.(l-shSarcctgshS) е к 1 -е2 -arcsine

Заметим, что величина ф имеет вид Uf{l)x. Тогда кинетическая энергия и, следовательно, присоединенная масса легко вычисляются по формуле

T=-nQ ф== у поа^и^ е-(arcsin е)

11=0 arcsin е-е ]/ 1 -

Обтекание сжатого эллипсоида легко получается путем наложения потока -I/ на найденное выше решение.

15.55. Круглый диск. Для круглого диска, движущегося перпендикулярно своей плоскости, в формулах п. 15.54 мы полагаем е=1, с = а. Таким образом, на передней стороне диска (о = 0) мы имеем

и кинетическая энергия равна

Г=-яд фdф = -Qai/г.

i ch g4-Sh2 I In th Sin2 T]

с c2 a+b+c

для сфероида, определяемого формулами =о. a=cchlo> bcshlo, движущегося со скоростью и в направлении оси х.

15.58. Параболоид вращения. Преобразование

х + 1со = с{1 + 1г\У

х = с{1-ц^), ffl=2cri,

и, следовательно,

х-с1= -

Таким образом, поверхности = const являются параболоидами вращения с фокусами в начале координат. Рассмотрим движение такого параболоида, перемещающегося со скоростью U в покоящейся жидкости. На границе параболоида 1=1о должно выполняться следующее условие:

Ф= -UAcXn, (1)

15.56. Трубка Вентури. Для отыскания решения уравнения (2) п. 15.54, которое не зависит от , мы полагаем /5 = 0, что тотчас же приводит к следующему результату:

ур = Ас cos т],

где Л -произвольная постоянная. Линии тока г^= const представляют собой гиперболы. Следовательно, поверхности тока представляют собой гиперболоиды, образованные вращением этих гипербол вокруг оси х.

Если мы зафиксируем некоторое значение л = Л о, то получим поток жидкости через трубку, стенкой которой является соответствующий гиперболоид, при этом наименьшее сечение, или горло, трубки является окружностью радиуса с sin г|о. Сечение трубки в окрестности горла может быть сделано сколь угодно малым. Для этого достаточно взять величину г\о достаточно малой.

Таким образом, мы имеем идеализированное представление потока через горло трубки Вентури (п. 1.70) или через рабочую часть аэродинамической трубы с большими скоростями.

Полагая Т1о = я/2, мы получим как предельный случай поток через круглое отверстие радиуса с в бесконечной плоской стенке (х = 0). Как обычно, в таких случаях скорость у края отверстия бесконечна (см. п. 6.10).

По определению функции тока ф поток через отверстие равен 2яЛс (1 -cos т1о), откуда определяется величина Л.

15.57. Функция тока для вытянутого эллипсоида. Вытянутый (или яйцевидный) эллипсоид, называемый также вытянутым сфероидом, образуется при вращении эллипса относительно его большой оси. Метод, указанный в п. 15.54, может быть применен и к этому случаю путем использования преобразования

х--/ш= ccht,. Поступая таким же образом, получим

в то время как функция тока должна удовлетворять уравнению

Полагаем в этом уравнении ф=/()п'; в результате последовательного интегрирования находим

и поэтому ф= 5* + с) Tj . Требование ф = О теперь не является условием

в бесконечности, так как сам параболоид вращения распространяется до бесконечности и возмущает жидкость. Следовательно, это условие должно быть заменено требованием, чтобы скорость обращалась в нуль на бесконечности для точек, не находящихся вблизи параболоида (рис. 305). Из п. 15.51 мы находим

qV -21.21= -Ь Т1(В? + Щ\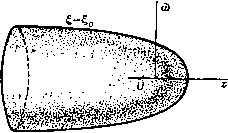

16c44c*g2 (24-Т)2)-

Первый член справа не обратится в нуль до тех пор, пока В Ф 0. Следовательно, мы должны положить В = 0.

ф = С^.

Сравнивая это равенство с формулой (1), получаем соотношение

Ф=-2с г/12л'.

Рис. 305.

В случае обтекания параболоида путем наложения равномерного потока скорости и, направленной справа налево, получаем

p=2cU {l-ll)r\\

Соотношение (3) также можно получить как предельный случай движения вытянутого эллипсоида следующим образом. Если поместить начало координат в фокусе, то преобразование п. 15.57 можно записать в виде

x-\-iZ = c cht,~-c= 2cshi.

Если написать 2kc вместо с и /k вместо , то получим

x-l-/m = 4cfe2sh2l,

и при k->co это выражение переходит в следующее л: + = с^.

По сравнению с функцией тока п. 15.57 здесь имеются следующие изменения: величины а, Ь, с теперь соответственно равны

2k4ch

2kcsh

2k4,

в то время как величины \, т] переходят в величины Tj/fe. При k получаем формулу (3).

оо

15.60. Теоремы сравнения. Рассмотрим безвихревой поток невязкой несжимаемой жидкости, ограниченной линиями тока, в некоторой области R плоскости ху. В области R нет ни источников, ни стоков.

Плоскость может быть плоскостью двумерного потока или меридиональной плоскостью осесимметричного потока, при этом ось х является осью симметрии.

Скорость течения справа налево через элемент dn нормали к линии тока ф = const равна е Зф/Зл, где е= 1, или е = смотря по тому - плоский поток или осесимметричный, так что величина е всегда положительна (рис. 306).

Заштрихованная область ограничена двумя непересекающимися линиями тока, каждая из которых имеет при л: = ± оо концевые точки.

Точку Р границы будем называть регулярной точкой, если она не лежит на оси (в случае осесимметричного потока), а находится на окружности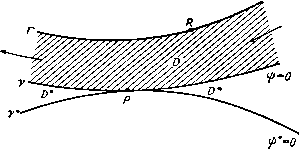

Рис. 306.

некоторого круга, касающегося границы в точке Р и внутренняя область которого целиком лежит в области R.

Функция тока ф удовлетворяет дифференциальному уравнению

Это уравнение эллиптического типа, и для его решения справедлив принцип максимума; а именно: если величина ф не константа, то она не может иметь ни максимума, ни минимума внутри области определения.

Физически это означает, что наличие такого внутреннего максимума или минимума привело бы к внутренней завихренности, что противоречит гипотезе безвихревого потока.

Таким образом, если ф равно нулю на одной границе и положительной константе на другой, то ф>0 во всей области между границами.

Теорема сравнения 1. Пусть D, D* - узкие длинные области, ограниченные соответственно линиями тока у, Г и у*. Г, и пусть область D содержится в области D*. Пусть два различных осесимметричных потока в областях D и D* определены функциями тока фиф*, так что

ф = 0 яа у, ф* = 0 яа Y*. ф = (2 = ф* на Г,

где Q - положительная константа; т. е. два потока имеют один и тот же расход. Предполагается, что эти потоки не накладываются друг на друга.

Если Р - регулярная точка, принадлежащая у и у* и если R - какая-либо регулярная точка на Г, то тогда для скоростей в точках Р и R двух потоков имеем

q{P)<q*iP), q{R)>q*{R); (2)