Если произведение 2та = ц остается постоянным при т-са и 2а - 0 то рассматриваемая комбинация становится двойным источником, или. диполем.

Соответствующие значения ф и ф могут быть легко получены следующим образом.

По теореме синусов мы имеем

2о

2а

sine, siTiei sin(e2-e,) as

2 sin -g (62 - eO COS 2 (Ог - 61)

/ j - Л2 =

Следовательно,

a (sin 62-sin Sj)

sin (62-6,) cosy (62-61)

2a cosy (62+61) cos- (62-6))

Ц cos-2 (62+61)

/1Г2 cosy (82 - 61)

m{x~a) /n(;c + a) 1(2 + 6.)

rir2C0Sy(e2-ei)

Если a->0, TO 62-Gi->9, rg->ri->r. Таким образом, для диполя имеем

ц cos 6

\х.х cos 6

г ~ гЗ ~ гЗ

Ось диполя направлена от стока к источнику. Эти результаты следуют также из теоремы Маклорена, если использовать замечание в конце п. 15.20. Так, если ф1 = 1/г, когда а мало, то

Точно так же

Линии тока для диполя изображены на рис. 296. Метод их построения изображен на чертеже того же рисунка. Положив ij3= - пй, где

n=l, 2, 3, .... проведем окружность диаметра ОЛ = р./(л(о), касающуюся оси диполя в точке О. Проведем РМ перпендикулярно OA и отметим, что

OQ = OM = OPs.mQ = OA sine.

Тогда если OQ = r, то

xsin3 9

и, таким образом, Q является точкой, лежащей на линии тока.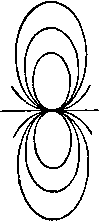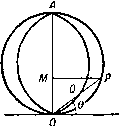

Рис. 296.

Отображением диполя относительно плоскости является равный по мощности, но антипараллельный диполь, который представляет собой оптическое отражение данного диполя, относительно плоскости (см. п. 8.42).

15.27. Твердые тела Рэнкина. Если мы скомбинируем равные по мощности источник и сток из п. 15.26 с равномерным потоком скорости U, направленным в отрицательную сторону оси х, то получим следующую функцию тока:

ij, = lf/r=sin2e-f-m(cose2-cos0i). (1)

Если точка Р находится на оси, то 9 = 0 или я, в то время как ©2 - Oi = О, за исключением точек, находящихся между источником и стоком, где Эа -9i = n;.

Таким образом, линия ф = 0 содержит всю ось х, за исключением части между источником и стоком, и, следовательно, дает разветвляющуюся линию тока, уравнение которой имеет вид

m2 + 6Mcos92-cos9i)=0, b = 2m/U. (2)

Так как величины cosOj и созЭа численно меньше единицы, то, следовательно, ю' не может превышать 2Ь^ и, значит, разветвляющаяся линия тока замкнута.

При вращении разветвляющейся линии тока относительно оси симметрии образуется разветвляющаяся поверхность тока, которая симметрична относительно плоскости л: = О, так как уравнение не изменится, если у величин т и и изменить знаки на обратные. Поверхность, вдоль которой ф = 0, можем заменить твердой стеной. Таким образом, мы построили обтекание

твердого тела вращения, которое в сечении имеет овальную форму (рис. 297), где Л -сток, В -источник. Это тело называется твердым телом Рэнкина.

Точки С и £>, в которых поток разветвляется, являются критическими точками. Для определения этих точек можно продифференцировать функцию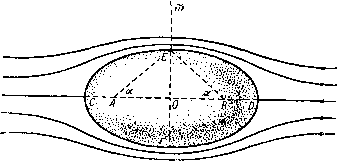

Рис. 297.

тока, или еще проще: поток в точке D нейтрализует скорость, обусловленную источником и стоком, так что если OD = l, ОВ=а, то имеем

т

или

(/j,-a)2 i (/ а)2 {1-ау=2аЬН.

Это соотношение определяет величину /, а следовательно, длину твердого тела. Если OE = h, то для определения ширины из уравнения (2) получаем 2&2 cos а = h, где а - угол ЕАО. Отсюда находим соотношение

2а

Vh+a

определяющее ширину.

Твердые тела, построенные вышеуказанным способом с помощью подходящего распределения источников и стоков, имеют как практическое значение, так и представляют интерес для теории, поскольку если известно распределение источников, то легко рассчитать скорость и давление. Сравнение расчетных результатов с наблюдениями показывает, что распределение давления хорошо согласуется с теоретическими расчетами давления на передней части. Отклонение имеет место только вблизи задней критической точки, где наблюдается внезапное падение давления ниже теоретического значения. Это падение давления обусловливает лобовое сопротивление тела, что имеет место на практике.

15.28. Эквивалентный слой Грина. Связная замкнутая поверхность S делит пространство на две области Ri и Rz- Пусть drii и йпг обозначают элементы нормали к поверхности S , проведенные соответственно в областях Ri и /?2- Тогда имеем

Пусть через и фа обозначены потенциалы скоростей ациклического безвихревого движения жидкости соответственно в областях Ri и Rz.

Опять эту формулу можно интерпретировать как результат действия распределенных источников и диполей. Таким образом, ранее найденный эквивалентный слой не является единственным.

Однако если мы возьмем фг = ф1 на поверхности S, то второй интеграл в формуле (5) обратится в нуль. Таким образом, если мы мысленно заменим поверхность 5 мембраной, то будем иметь на поверхности S соотношение -d)i/ds = -d(p2/ds, так что касательная скорость непрерывна, но нормальная скорость разрывна. В этом случае мы получаем единственное распределение источников мощности

- [dJdni -f- Зф2/5п2)/4я

на единицу площади, которое создает данное движение жидкости. С другой стороны, выберем фг таким образом, чтобы было {дщ/дщ-\- йфг/Лг) = О на поверхностиS. Тогда первый интеграл в формуле (5) обратится в нуль, и мы будем иметь непрерывную нормальную скорость, но разрывную касательную скорость на поверхности S , т. е. вихревой слой. В этом случае мы имеем единственное распределение диполей с моментами, равными (ф1 - ф2)/4п на единицу площади, которое может создать данное движение жидкости.

Вывод из этого результата состоит в том, что вихревой слой может быть заменен распределением диполей.

Если движение в области Ri является циклическим с интенсивностями циркуляции Xi, Хг, . . ., то мы можем использовать диполи, а не источники для получения формулы

(ФО. = i S (Ф-Ф.)aid) +1 S (I)+

(s) 01

Рассмотрим движение, задаваемое потенциалом ф^. Из формулы (2) п. 2.63 мы имеем

(s) (s)

если точка Р находится в области Ri, и

(s) (s)

если точка Р находится в области R.

Мы можем интерпретировать соотношение (2) следующим образом: в каждой точке области Ri потенциал скорости действительного движения такой же, как потенциал, который создается распределенным источником мощности (-5ф1/4п на единицу площади по поверхности S и распределенным диполем с моментом, равным ф1/4л на единицу площади, по поверхности 5.

Эти распределенные источник и диполь составляют эквивалентный слой источников и диполей Грина. Они дают действительную скорость в каждой точке области R и нулевую скорость в каждой точке области /?2-

Теперь возвращаемся к потенциалу ф2. Точка Pi, находящаяся в области Ri, является внешней относительно области R2, и, следовательно, формула (3) дает

(s) (s)

если точка Р находится в области Ri. Складывая формулы (2) и (4), получаем

Здесь ф1 - однозначная функция, определенная в области видоизмененной в односвязную с помощью введения барьеров Oj, Стг, ; фг - потенциал скоростей ациклического движения, созданного в области Rz путем приложения соответствующих нормальных скоростей к каждому элементу dS воображаемой мембраны, совпадающей с первоначальной поверхностью S.

15. 29. Теорема Бутлера для сферы. Для теоремы о круге в п. 6.21 имеется аналогичная теорема, применимая к осесимметричным движениям. Пусть / (г, 6) - данная функция двух сферических координат г и 8 и пусть а - данная положительная константа. Определим функцию

/* = /*(/-, е) = /(т' О-

Тогда можно высказать следующую тeopeмy).

Сферическая теорема Бутлера. Пусть имеется осесим-метричный безвихревой поток в несжимаемой невязкой жидкости, не имеющей твердых границ; поток характеризуется функцией тока фо = Фо (, 9), все особенности которой находятся на расстоянии, больишм, чем а от начала координат, причем в начале координат фо = О (г^). Если в поток ввести твердую сферу радиуса г - а, то функция тока имеет вид

Ф = Фо-Ф: = Фо(/-, 9)--фо(-, 9) . (2)

Доказательство. Требуется удовлетворить следующим условиям:

(I) поток, заданный посредством функции ф, должен быть безвихревым;

(II) ф = const при г = а;

(III) функция ф* не имеет особенностей вне сферы г = а;

(IV) скорость, соответствующая функции ф*, должна стремиться к нулю, когда г стремится к бесконечности, и функция ф* не должна определять поток через сферу в бесконечность.

Из п. 15.10 и формулы (4) п. 2.72 видно, что условие равенства нулю вихря, выраженное через функцию тока ф, имеет вид

0+- i(sel)- - и

Непосредственным дифференцированием легко доказать, что если фо удовлетворяет уравнению (3), то имеет место равенство

в силу этого выполняется условие (I); условие (II) также удовлетворяется, так как ф = О при г = а.

Так как г я а^/г являются точками инверсии относительно сферы г = а, отсюда следует, что если одна точка находится внутри сферы, то другая находится вне сферы. Таким образом, если все особенности функции фо находятся вне сферы, то все особенности функции ф* находятся внутри сферы. Следовательно, условие (III) удовлетворяется.

Что касается условия (IV), то необходимо отметить, что функция фо регулярна внутри сферы г = а и вблизи начала координат фо = О (г^). Следовательно, в бесконечности имеем ф* = О (1 /г). Тогда из п. 15.10 следует, что скорость в бесконечности, обусловленная функцией ф*, имеет порядок О (1/г*),

1) Butler S. F J., Ргос. Cambr. Phil. Soc, 49 (1953), 169-174.

Т. е. стремится к нулю, когда г стремится к бесконечности. Для величины потока

мы имеем qdS = О (1/г), что также стремится к нулю при оо.

Тот же метод доказательства показывает, что если все особенности функции фо {г, 9) находятся внутри сферы г = а и если фо = О (1 /г) для больших г, то формула (2) дает поток внутри сферы, если сферу г = а сделать твердой, границей. Здесь условие (IV) заменяется тем требованием, чтобы ф* давала конечную скорость в начале координат. Доказательство предоставляем провести читателю в качестве упражнения.

15.30. Сфера в потоке. Функция тока для равномерного потока, текущего справа налево, имеет вид г^ sin 0. Следовательно, если в поток поместить сферу г = а, то, согласно сферической теореме Бутлера, получим

ф = 1у/-зш9(1-). (1)

Замечаем, что эта функция тока обусловлена комбинацией равномерного потока со скоростью -U и диполя с моментом Уг На?, находящимся в начале координат. Таким образом, потенциал скоростей имеет вид

Ф = f/ ( г cos 9

дЗ cos е 2г2

Линии тока могут быть построены прямо по формуле (1), однако легче сначала провести линии тока диполя, как указано в п. 15.26, а затем применить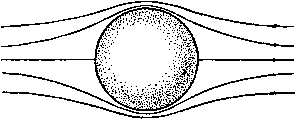

Рис. 298.

диагональный метод Рэнкина к потоку, являющемуся суперпозицией обоих потоков.

Скорость в каждой точке сферы направлена по касательной, и, следовательно, согласно формуле (2), ее величина равна -dff/rdQ = 3U sin 9/2.

Критические точки находятся на оси при 9 = 0 или при 9 = л;, и максимальная скорость скольжения равна 3U /2. Эта скорость достигается в экваториальной плоскости, перпендикулярной к направлению потока (рис. 298).

Давление в каждой точке сферы определяется формулой

р , 9t/2sin2 е П ..2

где П - давление в бесконечности. Точки минимального давления находятся в экваториальной плоскости, о которой упоминалось выше, и давление на экваторе равно Ро, причем

Po=п-ef/

И, следовательно, условие отсутствия кавитации такойо, что ро > О, т. е.

В соответствии с парадоксом Даламбера результирующая сила давления на сферу равна нулю. Сила давления на переднее полушарие выражается формулой

F= J pcosQ-2nasmQdQ = na(U-y о

Сила давления на заднее полушарие равна этой силе по величине, но противоположна по знаку.

15. 31. Кинетическая энергия. Если движение безвихревое, то кинетическая энергия жидкости, находящейся в какой-либо области, ограниченной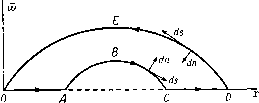

Рис. 299.

поверхностью вращения относительно оси, выражается, согласно п. 3.72, формулой

где dn - элемент нормали, проведенной в жидкости к элетенту dS площади, ограничивающей поверхности. В данном случае dS = 2n;cods, где ds - элемент дуги меридиональной криволинейной границы. Очевидно,

так как каждое из этих выражений представляет собой нормальную скорость. Следовательно, имеем

причем интеграл берется по той части меридиональной кривой, которая расположена с одной стороны оси (рис. 299) в направлении, указанном стрелками, при этом жидкость заключена между поверхностями, образуемыми кривыми ABC, DEO.

Если внешняя граница отсутствует, то интеграл тогда берется вдоль дуги ЛВС в направлении по часовой стрелке. Меняя направление обхода, получаем

Т = - фйф.

где теперь направление обхода берется против часовой стрелки.

и, следовательно.

f = 1m

причем сила f обращается в нуль, если u постоянно (рис. 300).

Если сфера падает под действием силы тяжести в бесконечной жидкости, то силами, действующими на нее, являются вес Mg, направленный вертикально вниз, архимедова сила, направленная вертикально вверх,

1) Тогда оно является относительно установившимся, см. п. 1.11.

Другое выражение для кинетической энергии Т только через функцию тока можно получить, если учесть, что интегрирование в формуле (1) по частям дает

7= - фйф,

так как обинтегрированная часть обращается в нуль. Далее, поскольку

1 aij)

TO отсюда имеем

При этом интеграл берется вдоль границы в направлении, указанном на рис. 299.

15.32. Движущаяся сфера. Если сфера движется со скоростью U в жидкости, покоящейся в бесконечности, то формулы для потенциала скоростей и функция тока выводятся сразу же из соотношений (1) и (2) п. 15.30 посредством наложения постоянной скорости U в положительном направлении оси х, так что получаем

1 г; cos 6 , 1 г/ ч sin2G

Важно заметить, что эти результаты относятся к началу координат, движущемуся вместе со сферой, так что, даже если U константа, то движение не является установившимся).

Кинетическая энергия жидкости, согласно п. 15.31, выражается формулой

л о

где уИ -масса жидкости, вытесненной сферой. Таким образом, полная кинетическая энергия системы твердое тело - жидкость равна

где уИ -масса сферы. Следовательно, виртуальная масса равна (M-i-VaAl) (см. п. 9.221).

Если через F обозначить сопротивление жидкости, то, приравнивая скорость изменения кинетической энергии мощности, получим

И сопротивление y-W, направленное вверх. Таким образом, получаем уравнение

так что ускорение равно

dU dt

где S -отношение удельных весов сферы и жидкости.

Этот результат показывает, что влияние жидкости сводится к уменьшению ускорения силы тяжести в отношении (s - 1): (s + V2)- В частности, если S < 1, то сфера поднимается с ускорением, определяемым вышеуказанной формулой. Этот результат имеет очевидное применение к движению воздушного шара.

Дарвин показал (см. стр. 237), что исследование, которое привело к формуле (9) п. 9.222, может быть применено к трехмерному телу, движущемуся в направлении оси х; для присоединенного объема получается соотношение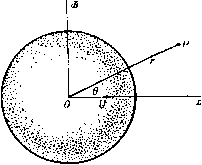

Рис. 300.

в котором сначала должно производиться интегрирование по х. Величина присоединенной массы равна qD.

В случае сферы = у яа^ и присоединенная масса, следовательно, равна /iM, как получалось выше.

15.33. Давление на движущуюся сферу. Уравнение для давления имеет

вид

Пусть Г = OP - радиус-вектор точки Р (фиксированной в пространстве) относительно центра сферы О. Тогда имеем

d<f дГ

1 аЗ

2 dt 2 dt 2л* dt

V=-gi{PO)=-,

и, следовательно, t/cos 6 - скорость точки О вдоль отрезка 0Р= -dr/dt.

Пусть f = би/5 - ускорение центра сферы. Подставляя это в (3), получаем

=-i?:rf-if/+gt/cose.

Подставляя этот результат в уравнение (1), находим

f-yrf + g-(3 COS е + 1) - (3 COSe - 1) = - ,

так как все члены, стоящие в левой части, за исключением первого, обращаются в нуль при г=оо.

Таким образом, давление на поверхность сферы выражается формулой

= i-af + lt/(9cose-5),

где а -точка сферы (г)г=а- Эти результаты также можно непосредственно получить из п. 3.61.

15.40. Отображение источника относительно сферы. Рассмотрим сферу радиуса а с центром в точке О. Пусть в точке А (/, О, 0) имеется источник мощности т и пусть Р - произвольная точка. Если прямая АР составляет угол 01 с положительным направлением оси, то функция тока для источника, подобранная таким образом, чтобы она обращалась в нуль в начале координат, имеет вид

фо = т(1--со8 Oi);

следовательно, по сферической теореме Бутлера, если в жидкость поместить сферу, то для функции тока получим

ф = т(1-Ьсоз ei)-m(l-i-cosei)* = = m + mcos6i - -m (cos6i)*. (1)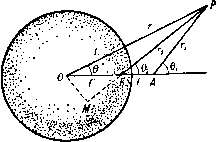

Рис. 301.

Оценка величины (cosOj)* не представляет особых трудностей, но решение этой и подобных задач, связанных со сферой, облегчается еще и некоторыми простыми геометрическими соображениями. На рис. 301 точка В является точкой инверсии для точки Л, так что

ff=a\

Проведем отрезки BL, ОМ перпендикулярно отрезкам ОР, РВ. Тогда точки О, М, В, L окажутся циклически сопряженными, так что

PO-PL = PB-PM.

г1 = /-2 + /2 2 - cos е, rl = r + р - 2/ г cos е, следовательно, из формулы (1) п. 15.29 имеем

а

а г

Кроме того, cos81= (/-cos6 -/) -! и, следовательно, из формулы (3) получим

/ а \* г /2 Q ,Л /л2 г PL г РМ

(COS ei)* = -(-cose-/j):L?=--.=--.-p.

Таким образом,

(cos9i)*=-= -Гсоз92-л2 5