\ пт J 3 V, ЗгяШ J 5 V,

56. Прямая трубка длиной I с одного конца сообщается с атмосферой. Через другой конец она сообщается с большим сосудом, в котором давление в момент времени t равно

П (1-а sin nt),

где П-атмосферное давление, а-малая постоянная величина. Найти потенциал скоростей для воздуха внутри трубки.

57. Горизонтальная трубка длиной / жестко закрыта с одного конца и открыта с другого. Показать, что периоды колебаний воздуха в трубке равны 4l/cN, где jV - нечетное целое число, с-скорость звука в воздухе.

Если в середине сечения трубки помещен тонкий поршень массы М (трение не учитывается), то показать, что периоды (2я/п) свободных колебаний даются формулой

Мп1 п1

-= 2Л1 ctg-

с с

Tit М'-масса воздуха в трубке.

58. Прямая трубка длиной I жестко закрыта с одного конца, а с другого конца закрыта пробкой массы М, которая может передвигаться без трения в трубке и находиться под действием пружины. Если нет воздуха, то пробка может совершать малые колебания с частотой п/2я. Если трубка наполнена воздухом массы М' при атмосферном давлении и другой конец пробки также подвержен атмосферному давлению, то доказать, что частота свободных колебаний выражается формулой

л> л ст ос М'

59. Прямая трубка длины / жестко закрыта с одного конца, а на другом конце имеется герметический поршень, который заставляют колебаться, причем его перемещение в момент времени t равно а cos nt, где величина а мала. Найти функцию, определяющую

причем ширина канала на поверхности равна Ь, а средняя глубина при этой ширине равна Л.

Устье, для которого Ь~х/а, h = yx/a, где 0<;д:<;а, а ри у-константы, сообщается с открытым морем при х-а, где поддерживаются приливные колебания вида

T] = Ccos {nt-{-e).

Показать, что приливные волны в устье определяются формулой

Ц = С . ., --г---cos (ni+e),

где к = п^а/£у (см. Лам б. Гидродинамика, § 186).

53. Изложить теорию длинных волн в канале постоянной глубины А, обусловленных возмущающим потенциалом Q = H ехр i (ai-Kx). Если дно заменить возмущающей силой, вызывающей отклонение Т1о = аехр i ot-Кх), то доказать, что относительная высота волн такая же, как если бы потенциал уменьшился в (1-ц) раз, где ц обозначает отношение а к равновесной высоте (-H/g), обусловленной возмущением. Доказать, что это справедливо не только для простых гармонических волн.

54. Взяв скорость звука с = 335 м/сек, вычислить длину органной трубы, открытой с обоих концов, основной тон которой имеет частоту 128 гц. Доказать, что основная частота не изменится, если в середине трубы поместить твердую перегородку. Объяснить физическую причину этого явления.

55. Показать, что возможными периодами воздушных колебаний в трубе, открытой с обоих концов и имеющей длину, равную 21, являются

г L L 2 3

где Т = 4 с, с-скорость звука в воздухе.

Если в центре трубы помещен без трения тонкий поршень массы М, показать, что периоды (2я/п) колебаний, отличных от симметричных, определяются из уравнения

, п1 , М'с

где М' - полная масса воздуха в трубе.

Показать, что если отношение М'/М мало, то эти периоды приближенно равны

скорость колебания воздуха в трубке, и показать, что кинетическая энергия находящегося в ней воздуха равна

я2 cosec2 --

СП , п1

sirfi nt,

где m-масса воздуха в трубке, а с-скорость звука.

60. Тонкий поршень массы М, помещенный в середине прямолинейной трубки, открытой с обоих концов, находится под действием пружины, жесткость которой подобрана так, что собственный период колебаний поршня в вакууме равен 2я/т. Показать, что если учитывать наличие воздуха, то собственный период 2я/п дается формулой

М(т2-n2) = 2QCrtStg

где 2/ -длина трубки, а S-площадь сечения.

61. Трубка длиной 21 закрыта с одного конца, открыта с другого и разделена на две части тонким, плотно пригнанным поршнем, скользящим в трубке без трения, но находящимся под воздействием пружины такой жесткости, что его собственный период колебания равен 2п/т. В положении равновесия поршень находится в середине трубки, и содержащийся в трубке воздух находится под атмосферным давлением. Показать, что период нормального собственного колебания 2я/п определяется из уравнения

-m2) = 2cnctg

где а-длина трубки, требуемая для того, чтобы масса воздуха, находящегося в трубке, равнялась массе поршня, а с-скорость распространения звука в воздухе при атмосферном давлении.

62. Определить, что произойдет, если система плоских звуковых волн упадет прямо на поверхность раздела двух газов, в которых скорости звука равны соответственно с и с'. Показать, что часть падающей энергии, равная 1с' - с)/(с'-с), отражается.

63. Если п/2я-частота волн, симметричных относительно начала координат внутри твердой сферической оболочки радиуса а, то показать, что имеет место равенство

. па па

64. Доказать, что в звуковых волнах малой амплитуды потенциал скоростей ф удовлетворяет уравнению

= с2У2ф.

Доказать, что величина ф в любой момент времени t в любой точке Р неограниченной среды дается формулой

4яф =

t F(ct)d(i, +t G{ct)da),

где интегрирование берется относительно телесного угла ш по сфере радиуса ct с центром в точке Р, а величины F, G соответственно обозначают начальные значения ф, d(f/dt.

Доказать, что в точке, где первоначально нет возмущения, интеграл по времени от величины сжатия по всему интервалу времени, в течение которого волны проходят через точку, в общем случае равен нулю.

65. Центр твердой сферы радиуса а в момент времени t находится в точке x = bsmnt, где 6 - малая величина. Доказать, что все условия для движения окружающего газа удовлетворяются потенциалом скоростей:

д f tn((-r/c)

cos 9,

где с-скорость звука. Л-постоянная величина. Найти величину,Л, механическую силу, необходимую для поддержания предписанного движения сферы, и работу, совершенную ею в одном из колебаний.

66. Точечный источник звука вызывает колебательное движение, потенциал скоростей которого равен

а cos k {d - г)

Показать, что средняя скорость переноса энергии через концентрическую сферическую поверхность равна 2ядск^а^. Один конец органной трубы открыт, а другой закрыт. Выяснить влияние открытого конца на периоды колебаний и показать, что для колебаний основного тона коэффициент затухания равен 16/*/яшс, где I-длина, а со-площадь поперечного сечения трубы.

67. Если потенциал скоростей (в сферических полярных координатах) для звуковых волн имеет вид / (г) е* cos 9, то показать, что

где k = n/c, А и В -произвольные константы.

Твердая сферическая оболочка радиуса а, содержащая воздух, совершает малые колебания, так что ее центр в любой момент времени находится в точке r = 6siпn 6 = 0.

Доказать, что потенциал скоростей воздуха внутри сферы равен

cosftr sinftrl ,

-Гг---) cose cos

где

C=nka4/{(2-ka) sin ka-2ka cos ka}.

68. Ha основании результата п. 14.61 доказать, что для длинных волн в канале справедливо уравнение

дх дх

Используя то обстоятельство, что правая часть не зависит от у, доказать, что частицы, находящиеся в вертикальной плоскости, перпендикулярной направлению распространения волн, остаются в этой вертикальной плоскости.

69. Если (и, р)-малые компоненты скорости для длинной волны, то, используя уравнение движения и предыдущий пример, показать, что

ди \ др dt]

~дГ~~дх~ ~дх

и что

di дх

где

о

Получить уравнение неразрывности в форме

=- §.

где /г-средняя глубина.

70. Используя предыдущий пример, показать, что имеет место уравнение

д(2 дХ

ИСХОДЯ из этого, доказать, что

= h(x+ct)+f2(x-ct).

Глава 15 ФУНКЦИЯ ТОКА СТОКСА

15.00. Осесимметричные движения. В предыдущих главах мы могли рассматривать двумерные движения с помощью комплексного переменного и комплексного потенциала. При рассмотрении трехмерного движения мы уже не можем пользоваться комплексным потенциалом. Простейшим примером трехмерного движения является движение, одинаковое в каждой плоскости, проходящей через некоторую прямую, называемую осью. Такое движение, например, имеет место, когда твердое тело вращения движется в направлении своей оси вращения в покоящейся жидкости.

Движение такого вида, называемое осесимметричньш, в некотором отношении аналогично двумерному движению; в частности, для движения можно определить функцию тока. Если движение безвихревое, то потенциал скорости также всегда существует.

В качестве оси х возьмем ось симметрии. Движение в этом случае удобнее рассматривать в сферических координатах (г, 9, со) или в цилиндрических (х, ш, ш) (рис. 43, 44).

15.10. Функция тока Стокса. Рассмотрим фиксированную точку А на оси симметрии и произвольную точку Р. Соединим точки Р я А кривыми AQP, AQiP, лежащими в одной плоскости (проходящей через ось) которую для удобства назовем меридиональной плоскостью (рис. 286). Положение точки в этой плоскости может быть определено цилин-

n дрическими координатами {х, ©). Если

> мы будем поворачивать меридиональные

ОД ) \ кривые AQiP, AQ2P относительно оси

! симметрии, то получится замкнутая по-

0 А ъ X верхность, в которую справа налево че-

рез поверхность, образованную линией Рис. 286. АС1гР, втекает такое же количество жид-

кости, которое вытекает в течение того же промежутка времени через поверхность, образованную линией ЛQlf. Предполагается, что жидкость не создается и не уничтожается внутри поверхности.

Если 2лф обозначает поток через одну из этих поверхностей, то функция ф называется функцией тока Стокса. Если мы сохраним линию AQiP неподвижной, а линию AQ2P заменим другой меридиональной кривой, соединяющей точки Л и Р, то очевидно, что величина ф не изменится. Следовательно, функция тока ф зависит от положения точки Р и, возможно, от положения фиксированной точки Л. Если мы возьмем другую фиксированную точку В на оси и проведем кривую BQ3P, то поток через поверхность, образованную линией BQ3P, будет равен потоку через поверхность, образованную линией ЛQlP, так как вследствие симметрии поток через АВ отсутствует. Отсюда следует, что величина ф не зависит от выбора фиксированной точки при условии, что эта точка лежит на оси симметрии. Поэтому величина функции тока в точке Р зависит только от положения точки Р, и если точка Р лежит на оси, то ф = 0.

Если через фр, фр обозначить значения функции тока в точках Р и Р', то поток справа налево через поверхность, образованную вращением относительно оси какой-либо линии, соединяющей точки Р и Р', равен 2яфр - 2яфр (рис. 287). Если считать, что точки Р и Р' находятся на бесконечно малом расстоянии 8s друг от друга, то нормальная скорость справа налево через РР определяется из формулы

2n<u6sqn = 2п (фр---фр), отсюда, переходя к пределу, получим

1 дуЬ

Как частное применение этого важного результата, полагая ds по очереди равным dco, dx, rdQ, dr, получим равенства

W да 1 аф

/-sine гае rsine дг

выражающие компоненты скорости в цилиндрической и сферической системах координат (рис. 288). Компоненты скорости, перпендикулярные мери-

так как через такие линии течение отсутствует. Величина ф имеет размерность иТ, а потенциал скоростей ф -размерность LT.

Следует заметить, что функция тока ф существует в силу неразрывности движения и, следовательно, уравнение неразрывности автоматически удовлетворяется. Заметим также, что из вышеуказанных значений компонент скорости можно получить соотношение

= 0,

которое являeтcif другой формой уравнения неразрывности.

Функция тока была определена относительно основной точки на оси. Смещение основной точки изменит значение ф только на постоянную величину (см. п. 4.30). Поскольку используются только разности и производные от функции ф, то удобно рассматривать ф как функцию, содержащую аддитивную произвольную постоянную.

15.20. Простой источник. Простым источником называется точка, из котопой жидкость вытекает по падиусам во все стопоны. Если источник

выделяет в единицу времени объем жидкости, равный 4я/п, то т называется мощностью источника ).

Стоком называется точка, в которую жидкость втекает по радиусам.

Если в начале координат имеется источник мощности т, то направленный наружу поток через сферу радиуса г, центр которой находится в источнике, связан с радиальной скоростью формулой 4я/п = 4пг2(7г (рис. 289).

Таким образом, имеем

1 т

гsin6 гае ~72

откуда получаем

(f = - , ф = /п COS д = - .

Функцию тока можно получить также, непосредственно рассматривая поток через сферическое тело, пересекаемое плоскостью, проходящей через точку Р и перпендикулярной оси Ох.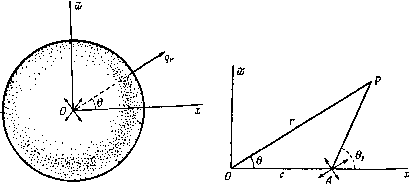

Рис. 289.

Рис. 290.

Если источник находится не в начале координат, а в точке А, то мы получим (рис. 290)

АР Угс22сгсозв m (г cos в-с)

ф= mcosOi =

Переходя к координатам х и со, получаем

m .,. т(х-с)

У{х-с)+Ъ^ ш содерж

аф аф

У(х-с)+(й^

Заметим, что эти функции содержат х я с только в виде разности (дг -с). Отсюда

дх

Отображением источника относительно плоскости является равный по мощности источник, получающийся оптическим отражением исходного источника относительно плоскости (см. п. 8.40).

1) Таким образом, производительность источника М = 4пт. Некоторые авторы называют величину М мощностью (см. прим. на стр. 196).

15.21. Подводный взрыв. Если полость в форме сферы радиуса Rq, содержащая газ под давлением ро> начинает быстро расширяться в неограниченной жидкости, то мы имеем имитацию действия подводного взрыва. Пусть i? -радиус полости в момент времени t, pi -давление газа. Будем считать, что газ расширяется по адиабатическому закону, а силами инерции можно пренебречь. Тогда, согласно закону адиабатического расширения, имеем

Ро ~ V V

Если пренебрегать силой тяжести, то жидкость будет двигаться по радиусам, причем скорость на границе области равна dR/dt=R. Таким образом, это движение будет аналогично движению жидкости в случае источника, и мы можем положить

т dw т

Следовательно, если r = R, то tn/R = R. Отсюда

дц, RW + 2RR

Тогда уравнение для давления запишем в виде

Q + 2 V

RR 2 RR + 2RR д,/.х г2 J г

Если давление на бесконечности принять равным нулю, то функция F (t) равна нулю, так как это есть величина, стоящая в левой части уравнения при г = оо. Полагая r - R, мы будем иметь p = pi, и, следовательно,

+ /?- = ;.f.

Умножим обе части этого уравнения на 2RR и введем константу po/Q. Тогда получим

dt i?3Y-2

Замечая, что /?=0 при R = Ro, после интегрирования найдем

R J Г/лз /-лзу-] с2 -3{Y-1) R J \ R J I

Если у = */з, то решение можно получить в замкнутой форме, положив R = {I + п) Rq, что дает соотношение

в качестве иллюстрации положим ро= 1000 агтгм и Ro = 50 см, тогда получим с = 3,16x10* см/сек, причем радиус полости удваивается за 0,004 сек и начальное ускорение точек поверхности равно 2,00 X 10 см/сек', что оправдывает пренебрежение силой тяжести.

15.22. Равномерный поток. Пусть имеется равномерный поток со скоростью и, паралельной оси Ох, причем жидкость течет справа налево через окружность радиуса со с центром на оси Ох. Плоскость окружности

перпендикулярна оси Ох. Тогда мы имеем 2пг) = - тоЮ, и, следовательно,

-аЮ =-Ursind. (1)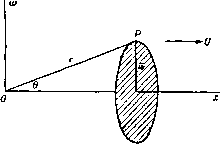

Рис. 291.

Этот результат может быть также получен при интегрировании уравнения

(О д(й

и.

Потенциал скорости равен

Ф= -Ux= -UrcosQ.

15.23. Источник в равномерном потоке. Если мы поместим источник равномерный поток, то получим (рис. 292)

г|)= -UrsmQ + mcos 9.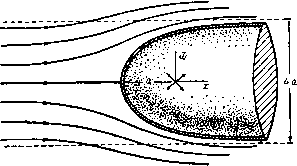

Рис. 292.

Критической точкой называется такая точка, в которой qr = 0, qe=0, или

[/cos9+ = 0, -f/sin9 = 0,

откуда следует, например, 9 = я, = m/U = а^.

Линия тока, проходящая через критическую точку, удовлетворяет уравнению

- Ur sin* Q+mcosQ= - Ua\

Это разветвляющаяся линия тока, уравнение которой может быть записано в форме

= 20(1 4-cos 9),

и, следовательно, если 9->0, то со2а, т. е. получаем асимптоты.

Разветвляющаяся линия тока изображена на рис. 292, она легко может быть построена по методу Рэнкина или по уравнению

г = а cosec

Следовательно, уравнение (1) дает обтекание тупоносого цилиндрического тела, диаметр которого равен 4а.

Уравнение для давления имеет вид

откуда следует, что p->U с увеличением г.

Это уравнение можно использовать для тарировки трубки Пито при различных положениях боковых отверстий, причем отверстие у носа измеряет величину П + Y 6, то время

как боковое отверстие измеряет величину р.

Уравнение (2) также можно использовать для расчета распределения давления вблизи носа дирижабля, в Q а *

15.24. Линейный источник конеч- Рис. 293.

ных размеров. Рассмотрим линейный

источник, простирающийся вдоль оси от точки О до точки А, при этом мощность источника, отнесенная к единице длины на расстоянии от точки О, равна mt,/a, где а=ОА (рис. 293).

Функция тока получается наложением функций тока ряда элементарных точечных источников мощности т^б^/а, и, следовательно,

ф = mcosadg.

где а -угол PQx, OQ=g. Так как

= х -(Dctga, = О) cosec ada,

то мы имеем, что

а-2 ~

, 1С со cosa J

если т% известная функция от , то можно выполнить интегрирование. Самым простым случаем является случай, когда т| = const =/п, тогда

SinOj sin 02

{РО-РА).

Линиями тока являются гиперболы с фокусами в точках О и Л. Если мы наложим равномерный поток скорости t/, то получим

г|,= .(7r2sin2 9 + {РО~РА).

Отрицательная часть оси х должна быть частью разветвляющейся линии тока, и, следовательно, она должна соответствовать значению ф =-т. Разветвляющаяся линия тока определяется уравнением

Сй2 =

2т

и

РА = г^+а^~ 2аг cos ai, РО = г. Отсюда для больших значений г получим

PO-PA=r-r(\~i-... = acosai+0{r-).

Если точку Р удалять в бесконечность, то aj->0.

Таким образом, разветвляющиеся линии тока имеют следующие асимптоты:

Таким образом, мы опять имеем обтекание цилиндрического тела, имеющего более заостренную носовую часть, чем изображено на рис. 292.

15.25. Дирижаблеобразные формы. Рассмотрим совместно равномерный поток в положительном направлении оси х, точечный источник мощности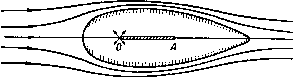

Рис. 294.

т, находящийся в начале координат, и линейный сток с общей постоянной мощностью -т, распространяющийся от начала координат до точки к=а. Тогда функцию тока можно записать в виде

= :LuS-{po-pa)+.

Если точка Р расположена на положительной части оси х, то х=г, РО - РА =а; если Р находится на отрицательной части оси х, то х= -г, РО-РА= -а.

Таким образом, линия ф=0 содержит всю ось х; разветвляющаяся линия тока состоит из оси х и замкнутой части дирижаблеобразной формы (рис. 294).

Используя другие законы изменения для линейного стока, при условии, что его полная мощность остается равной мощности источника, можно получить обтекание тел различной формы.

15.26. Равные по мощности источник и сток. Диполь. Другая простая комбинация состоит из источника мощности т в точке (а, 0) и стока мощности-m в точке ( - а, 0).

Используя обозначения, указанные на рис. 295, мы получим формулы

ф = m (cos 02 - cos Qi),

Ф = m---

с помощью которых легко можно построить линии тока.