жение типа прогрессивной волны. Чтобы сделать это, напишем формулы (3) и (4) в виде

отсюда имеем

Z = J5+aexp{/fi)(a + /)},

(8) (9)

Если исключим величину (а + t), то увидим, что W есть функция только от (Z + gt/a), так что волна распространяется налево со скоростью g/a.

W = ©2а2 (а + О + - ехр {- ia {a + t)}.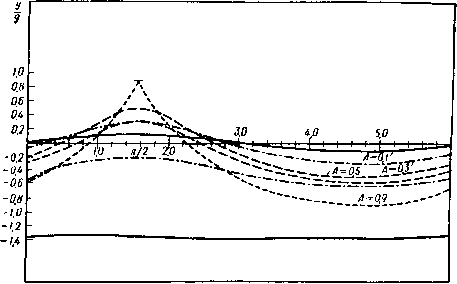

Рис. 284.

Поскольку особые точки теперь не являются неподвижными, мы должны связывать движущуюся поверхность дна с волной. При малых значениях отношения а/К поверхность дна может быть взята так глубоко, что движение сведется к бесконечно малому движению жидкости бесконечной глубины. Фазовая скорость g/(i) равна (gX/2n)V2, как и по классической теории.

При движении, задаваемом формулами (3) и (4), величина а является координатой Лагранжа только для действительных значений, соответствующих частицам, находящимся на свободной поверхности. Движение поверхностных частиц аналогично движению трохоидальной волны Герстнера (п. 14.81), задаваемой формулой

z = g + flexp {1(л(а+ /)},

где а - координата Лагранжа даже для комплексных значений, а результирующее движение жидкости является вихревым.

14.84.Точная нелинейная теория волн постоянной формы. Рассмотрим волну постоянной формы, движущуюся справа налево со скоростью с по поверхности бесконечно глубокой жидкости.

Предположим, что волна имеет вертикальную ось симметрии, проходящую через гребень С. Длина волны % есть расстояние, например, между двумя последовательными впадинами Т1НТ2, расположенными по обе стороны от гребня С (рис. 285).

Наложим на всю систему координат скорость с, направленную слева направо. В результате форма волны сделается неподвижной, а жидкость в этом движении (т. е. в системе координат, связанной с волной) окажется текущей слева направо с некоторой средней скоростью с.

Возьмем ось х в направлении этой средней скорости с и ось у направим вертикально вверх через гребень. Пусть Я - высота волны, т. е. расстояние по вертикали от гребня до впадины.

Форма профиля свободной поверхности считается неизвестной. Отобразим этот неизвестный профиль Т^СТ на известную кривую - окружность единич-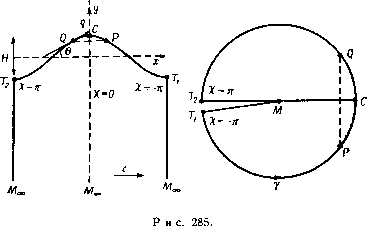

Z-плоскость

С- плоскость

ного круга в плоскости Если Т^М^о, TzM оо - вертикали, проходящие через впадины, то будет удобно называть областью одной волны область, ограниченную этими вертикалями и профилем волны.

Отобразим область одной волны на внутреннюю часть единичного круга с разрезом вдоль некоторого радиуса. Мы утверждаем, что точка Ма> отобразится в центр М единичного круга, а линии М ооС будут соответствовать радиусу МС, который лежит вдоль действительной оси в плоскости . Таким образом, если

1 = ге

ТО мы будем иметь х= О на радиусе МС. Тогда разрез МТ расположится вдоль радиуса, противоположного радиусу МС. Мы будем представлять себе края разреза находящимися на небольшом расстоянии друг от друга и образованными радиусом MTi, на котором х= -л, и радиусом МТ2, на котором %= я.

Тогда, если мы движемся по окружности единичного круга у, изменяя % от -я до я, т. е. следуя по линии Т1СТ2 в плоскости , то точка z будет описывать профиль волны Т1СТ2 и при переходе от Ti к Гг величина х уменьшится на длину волны Я. Это может быть достигнуто с помощью отображающей функции

= 1п^.

Та же самая функция преобразует точку = О в точку М . Таким образом.

отображение можно осуществить с помощью формулы

2=§(1п^+а, + а. + азг^+...) , (2)

где, как окажется, для получения симметричного профиля коэффициенты а„(п=1, 2, ...) должны быть действительны. Далее, получаем

5-=2(1 + + + +--0 = 2ST- (3)

где

/(Q=l4-Ci + a2C + G3S+.... (4)

На свободной поверхности полагаем

= ст = еЧ а=1/а. (5)

Тогда из формулы (2) для точки на свободной поверхности {х, у) имеем

- (x + aiSinx + 4- 2sin2x-f4 3Sin3x + .. Л ,

y = 2(aiCosx + -2a2COs2x+3-a3Cos3x+... j ,

и это доказывает симметрию относительно радиуса СМ или оси % = так как X изменяет знак вместе с х, а г/ не изменяет знака. Это утверждение справедливо только в том случае, если все величины а„ действительны. Далее, из формул (3) и (5) на свободной поверхности получаем

dz dz da iX f{a) . r / ч /тч

Теперь, если положить

fio)Rei, (8)

где и 6 действительны, то мы замечаем в силу формул (5), что R н Q являются функциями от %, так что имеем

R = R{X), 6 = в(х). (9)

Кроме того, логарифмируя формулу (8), мы получаем в точке а = е' следующее соотношение:

ln/?(e)-l-i6 (е)= 1п/(е*) = 1п(1 + а,е< + а2е2* + ) =

где

bi = ai, 62 = 02 -Y i> 63 = 03 -aica+ya?..... (10)

так что все величины 6 действительны и известны, если известны величины а„. Таким образом, находим

\nR(s) =bi cos e-f-62 cos 26 +63 sin Зе -}-..., (11)

e(e) = 6isine+62sin2e-f 6з51пЗб-Ь---- (12)

Для получения соотношения между 6 и i? можно использовать формулы (И) и (12) следующим образом. Из формулы (И) мы имеем

1п (е) = - bi sin 8 - 262 sin 28 - З63 sin Зе - ... .

о

де ц-произвольная постоянная.

WЩ-ШW sin9(co)d + i], (20)

sinnesin п% g.g j gjj 2e + З63 sin 3e + ...) de = яЬ„ sin х-

Следовательно, получаем

о n=l

= 6isinx + 62sin2x + 63 sin3x+... =e(x). (13)

Будет установлено, что формула (13) является ключом к решению нашей задачи. Отметим, что до этого момента мы изучали только свойства отображения. Рассмотрим теперь движение жидкости.

Если на поверхности положить ф = О, то граничные условия примут

вид

ф = 0, г=1 на поверхности, (14)

ф = 0, г=0 в точке Моо, (15)

u - iv=c, 2=0 в точке Моо- (16)

Всем этим условиям удовлетворяет комплексный потенциал

W=-\nt, (17)

что дает ф = - (сА,/2я) In г. Это выражение удовлетворяет условиям (14) и (15). Отсюда, а также из формулы (3) следует соотношение

-5?--Зс-Ш

При 2 = 0 имеем /(2)=1, так что условие (16) также удовлетворяется. Кроме того, из формул (18) и (8) следует, что на поверхности имеет место равенство

u - iv = - = - p- f{a) R

и, следовательно,

q=ciR, (19)

где 9 -угол между вектором скорости и горизонталью.

На свободной поверхности давление постоянно, и, следовательно, теорема Бернулли дает <72 + 2g£/ = const или, учитывая (19), {clR})-\-2gxj = = const, откуда после дифференцирования и применения формулы (7) находим

что можно записать в виде

Проинтегрировав это уравнение от О до е, получим формулу

sin е (е)

sin пг sin п%

о 1 -Ьц ] sine (аз) dm =i

О

Это - нелинейное интегральное уравнение для 9(х) (наклона волны) как функции х^)- После решения этого уравнения величины Ьи Ьг, Ьз, находятся из уравнения (12), затем находятся величины Сг, аз, ... из (10) и, наконец, профиль волны из уравнений (6).

Кроме того, если известны величины а^ а^, Оз, ..., то, согласно формуле (4), известна функция / (Q и, следовательно, находим скорость в любой точке по формуле (18).

Таким образом, оказывается, что вся точная теория волн постоянной формы^) вытекает из решения нелинейного интегрального уравнения (21).

Чтобы найти кинетическую энергию, мы должны вычесть наложенную скорость с, так что в результате имеем

q= (ы -c)*-f-t;*= (u - iv -с) (u + iv - c).

Но из уравнения (18) получаем и -iv= c/f (1,). Следовательно,

q=c4i-f{Q] u-nmf mm-

Теперь, если через dS и dA обозначить соответственно элементы площади волны и единичного круга, то из уравнения (3) и п. 6.29 следует равенство

dS dA

%/(?)f(0.

1) Это уравнение А. И. Некрасова, Изв. Иваново-Вознесенского политехи. ин-та 3 (1921), 52-65; 6 (1922), 155-171 (см. также переработанное издание этих статей: Точная теория волн установившегося вида , статья 19 в Собр. соч. А. И. Некрасова, т. I, Изд-во АН СССР, 1961.-Лр л. перев.).

*) Точной теорией установившихся гравитационных безвихревых волн занимались также Т. Леви-Чивита, Н. Е. Кочин, Струик, М. А. Лаврентьев и другие советские и зарубежные авторы. Обзор этих работ и соответствующую литературу можно найти в монографиях: Сретенский Л. Н., Теория волновых движений жидкости, ОНТ, НКТП СССР, М. Л., 1936; Стокер Дж. Дж., Волны на воде. Математическая теория и приложения, ИЛ, М., 1959, а также в статьях: Сретенский Л. Н., Волны. Механика i СССР за тридцать лет (1917-1947), М., 1950, стр. 279 - 299; W е h а и s е п J. V., La it one Е. V., Handb. d. Phys., Bd. IX, 1960 и др. Перевод ряда иностранных работ последних лет, интересных новыми идеями и методами, помещен в сборнике переводов. Теория поверхностных волн , ИЛ, М, 1959. Весьма интересной в этом сборнике является также вводная статья Н. Н. Моисеева, в которой дан обаий обзор работ, помеш.ен-ных в сборнике, и кратко освещены соответствующие по тематике оригинальные работы советских авторов. См. также Wehausen J. V., Recent developments in free-surface flows, Univ. California, 1963.

В двух монографиях и статьях, упомянутых здесь, дан также обширный материал по линейной теории волн.-Прим. перев.

Сравнивая формулы (13) и (20), мы видим, что величину R (е) возможно исключить и, таким образом, получить уравнение для 9(х). Чтобы сделать это, прологарифмируем обе части уравнения (20) и продифференцируем по е. Тогда получим

-31п/?(е) =-.

l-f-p, J sin 6(0)) dco О

Подставляя это выражение в формулу (13), находим

.......

К (в. х)= 2 т 1 (2)

Это следует из того, что тождество

1п(1 е -)=-2 QSl!l±il}

, п W cos яаз

ln2sin= -2 -1Г-

Если здесь последовательно положить © = 8-f-x и со = е - хи результаты вычесть один из другого, то получим

X 1 , 1 , 1-COS (г 4-Х)

(IV) Обозначив ядро через К %), мы можем записать уравнение (21) в виде

б (X) = г j-- (24)

о l-f-ц I sine(co) dffl б

Для Простоты здесь рассматривался случай бесконечной глубины. В случае конечной глубины h следует поступать аналогично, отображая

1) Расчеты проводятся в настоящее время (1959) в Математическом исследовательском центре.

*) Более точная формулировка следующая: не существует решения, отличного от решения е = О, и регулярного в замкнутом промежутке 0<9<2я и 0<f*<3 (см. работы А. И. Некрасова в прим. перев. на стр. 409).-Прим. перев.

Следовательно, кинетическая энергия одной волны выражается в виде

одна волна Y

у, е£2Х2 J lf(Q-l]Up-ndA 22)

Замечания.

(I) Соотношение (4) п. 14.58 и нелинейное условие Леви-Чивита на поверхности представляют собой постановку задачи для решения уравнения в частных производных. Задача, представленная нелинейным интегральным уравнением (21), совершенно отлична от указанной выше задачи для уравнения в частных производных в том смысле, что она является одной из тех, которые могут быть численно решены на современных быстродействующих вычислительных машинах*).

(II) Указанная задача является задачей на собственные значения; действительно, можно показать, что решения, отличного от решения 9 = 0, не существует при ц<3).

(III) Ядро интегрального уравнения (21) можно представить в виде

е(х, v)=(v-4v+Hi8v3)sinx-

+ (sV - А 0 + 44f4 Зх. (25)

(VI) Из соотношения (25) видно, что если величиной и более высокими степенями v можно пренебречь, то решение уравнения (21) имеет вид e(x) = §sinx, где р-малая постоянная величина.

(VII) Комбинация формул (И) и (20) дает соотношение

е

l+H sine(o))dco = -exp[-3(6icose-b62cos28+. ..)], (26)

где выражение, стоящее справа, никогда не обращается в нуль. Следовательно, выражение, стоящее слева, также никогда не равно нулю, будучи положительным при ц > 0. Заметим, кроме того, что величину можно получить из уравнения (26).

(VIII) Если в соотношении (26) положить е = 0, то сразу получаем, что ц является положительным числом.

(IX) Из уравнения (21) следует, что

е(2я-х)=е(х), 0(О)=е(д) = о.

Поэтому достаточно знать величину 6 (х) в интервале 0 < х < л;, и, таким образом, уравнение (21) можно заменить следующим уравнением:

е (X) = § f--K(e,%)dB, (27)

о 1-f (j. J sine(co)dco 0

что упрощает численные расчеты.

(X) В синусоидальной волне форма профиля вблизи гребня подобна форме профиля вблизи впадины. Так как в силу уравнения (21) 6(я -х)¥= ¥=в(х), то это свойство не сохраняется для волны, определяемой точной теорией [см. формулу (4) п. 18.65].

1) В этом соотношении коэффициент ggjgg Р С должен быть заменен его

исправленным значением (Собр. соч. А. И. Некрасова, т. I, Комментарий редак-

цин к статье \9.)-Прим. перев.

одну волну на кольцевую область, заключенную между двумя концентрическими окружностями и имеющую разрез вдоль радиуса. Это приводит к уравнению типа (24), но с ядром, зависящим теперь не от синуса, а от функции Вейерштрасса ст.

(V) Если в уравнении (21) написать

H = 3 + v, 0<v<l

и положить

э (х) = 9 (X, V) = (х) + ve (X)+v e3 (х) + ,

то, приравнивая члены при одинаковых степенях v в левой и правой частях уравнения, получим бесконечную систему интегральных уравнений для функций 01 (х), 92(х)> которую можно решать последовательно.

Учитывая члены, содержащие v, мы получаем сходящийся процесс при v< 1, что приводит к следующему соотношению ):

(XI) Поскольку уравнение (21) не линейно, мы не можем складывать решения.

14.85. Точная линейная теория. Этот термин мы применяем к теории волн малого наклона, получаемой по точному методу п. 14.84. Если в(х) - малая величина первого порядка, то мы имеем sin9(x)=9(X) и, следовательно,

е

sin9 (со) do)

- также малая величина первого порядка.

Таким образом, с точностью до величины первого порядка малости имеем

sin 9(8) / [l-tlij sin9 (co)dco] =9(е). о

Поэтому нелинейное интегральное уравнение (21) п. 14.84 сводится к однородному линейному интегральному уравнению

2я оо

е(Х)-9(е)2 T de. (1)

Если в этом случае положить 9 (е) = sin se, то получим

9(X) = 3nsinsX,

и, следовательно, 9(x)=sinsX является решением тогда и только тогда, когда n = 3s. Таким образом, уравнение (1) имеет собственные значения

1 = 3, 6, 9, ..., 3s, ...

и соответствующими собственными функциями будут

sinx, sin2x, sin3x, .... sinsX.....

Ввиду того что полный круг Y на рис. 285 соответствует одной волне, мы должны положить ц - 3 [см. п. 14.84, замечание (VI)] и тогда

e(x) = psinx, (2)

где р -малая величина первого порядка. Тогда из формулы (12) п. 14.84 мы найдем, что с точностью до величины первого порядка все величины обращаются в нули, за исключением 6i=p, и, следовательно, все величины а, обращаются в нули, за исключением Ci = 6i = p.

Таким образом, из второго уравнения (6) п. 14.84 на свободной поверхности следует г/ = (А,/2я) р cos %.

Если взять разность значений у при X = О (в гребне) и % = я {во впадине), то найдем, что высота волны выражается формулой Я=(Я/я)Р и, следовательно,

Р = пН/Х. (3)

Возвращаясь к формулам (6) п. 14.84, найдем параметрические уравнения для профиля волны

-{K/2n)%-HsinX, /=Ясо5Х. (4)

Это - трохоида, а не синусоидальная кривая, как в обычной линейной теории, рассмотренной ранее в этой главе (см. волна Герстнера, волна Джона).

Можно ввести амплитуду а, положив

Н=2а. (5)

Чтобы найти скорость распространения, положим в формуле (6) п. 14.84 ц=3, б1=р=2лаА, е=0.

Тогда получим

с^ = -еб А. (6)

Сравнивая эту формулу с формулой c=gk/2n, полученной по обычной теории, мы видим, что они согласуются при малых значениях а/к, и замечаем, что скорость поверхностных волн на глубокой воде увеличивается с увеличением отношения амплитуды к длине волны.

Для вычисления кинетической энергии воспользуемся формулой (22) п. 14.84. Из формулы (4) п. 14.84 имеем

/(P-l = ai = PS;

здесь площадь единичного круга равна я. Следовательно, использование формул (3), (5), (6) дает

у, 1 еХР1,еяад (7)

Эта величина Т отличается от величины, найденной в п. 14.20, на показательный множитель.

Для потенциальной энергии из формулы (4) мы имеем

У = -1 г/2 = agQl = Ге-бяо/х, (8)

о

Таким образом, при используемых здесь данных V ФТ.

14.86. Звуковые волны. Будем предполагать, что звуковые волны распространяются в газе посредством малых движений материальной среды, при которых частицы движутся вперед и назад на одно и то же расстояние. Благодаря такому характеру движения возмущение быстро распространяется, не вызывая переноса самой среды. Сделаем следующие основные предположения:

(I) Изменения давления, плотности и скорости от их равновесных значений Ро. 6о. О есть бесконечно малые величины первого порядка, степенями и произведениями которых можно пренебречь.

(И) Движение является безвихревым.

(III) Давление есть функция плотности; в частности, примем адиабатический закон р=щУ.

Из предположения (I) следует, что квадратичными членами в уравнении движения мы пренебрегаем, и, следовательно, отбрасывая внешние (массовые) силы, получим

dt Q

Кроме того, согласно допущению (II), имеем

+ Vq = 0, (3)

ds -9

Пренебрегая более высокими степенями s, из допуш,ения (III) имеем приближенно

p=xQV=ev(l+s)v = po(l+Ys). Таким образом, уравнение (1) дает

5=Л, с^Ш. (4)

Исключая S из соотношений (3) и (4), получаем

= cVY (5)

Этому уравнению удовлетворяет потенциал скоростей ф при распространении звуковых волн.

14.87. Плоские волны. Если звуковые волны распространяются только в одном измерении, скажем параллельно оси у, то уравнение (5) п. 14.86 принимает вид

dt дх

Решением этого уравнения (см. п. 14.60) является функция

Ф = ф1 {X-Ct) + ((>2{X + Ct),

где ф1 и фа - произвольные функции. Это решение представляет собой движение двух систем волн, из которых одна, отвечающая потенциалу скоро-

И, следовательно,

Умножив это уравнение скалярно на dr, мы получим

--(d9) = jdp.

Отсюда, принимая во внимание, что разность р - ро бесконечно мала, путем интегрирования находим

р

Р dp р-Ро

dt ] Q Qo Ро

Следовательно,

p-po=Qo (I)

Для плотности мы можем написать соотношение

Q=Qo(l+S), (2)

где S -бесконечно малая величина.

В этих обозначениях уравнение неразрывности (5) п. 3.20 принимает вид

jds dt

или