\udt=\\.cdt.

Интеграл, стоящий в правой части этого равенства, дает величину заштрихованной площади на рис. 277, и, следовательно, перемещение частицы получается посредством деления величины площади профиля, который проходит точка Р, на величину глубины невозмущенной воды. Когда волна

1) Такие же соображения о длинных волнах, основанные на применении этого ]>е>ультата, указаны в примерах 68- 70 к гл. 14; см. также п. 14.70.

показывающее, что давление на глубине {h + ц - у) равно гидростатическому давлению. Иначе говоря, вертикальным ускорением можно пренебречь

14.62. Поверхностное возвыщение. Из формулы (7) п. 14.60 для потенциала скорости имеем

(p=-(pi{x + ct) + ((i2(x-ct). (1)

Следовательно, поверхностное возвышение, согласно п. 14.12, выражается формулой

n = j{(fx{ + ct)-%{x-ct)). (2)

Таким образом, поверхностное возвышение представляет собой сумму возвышений, обусловленных двумя прогрессивными волнами, начальные формы которых имеют вид

Эти волны распространяются в противоположных направлениях со скоростью с, определяемой формулой

c=gh.

Характерное свойство длинных волн состоит в том, что скорость волны зависит только от глубины воды, а не от длины волны.

Из формулы (1) также следует, что скорость частиц жидкости и (обязательно горизонтальная при наших предположениях) выражается в виде

и==-VAx + ct)-q>Ax~ct). (3)

14.63. Волны, распространяющиеся только в одном направлении.

Рассмотрим волну, распространяющуюся в положительном направлении оси X. Если ы -скорость жидкости, т) - соответствующее поверхностное возвышение, то из формул (2) и (3) п. 14.62 получим равенства

и=-(р'(x - ct), 1]= (x - ct),

и, следовательно, и = gTi]/c= сцШ, так как c = gh. Таким образом, для волны, распространяющейся в положительном направлении оси х, будет справедлива формула

Чтобы проследить за движением частицы, первоначально находящейся в точке Р невозмущенной поверхности воды в прямолинейном канале, мы замечаем, что перемещение равно

окончательно пройдет, частица окажется перемещенной вперед относительно ее начального положения иа расстояние, равное отношению объема поднятой воды к площади поперечного сечения воды в канале.

Из формулы (1) также следует, что u.h= gtf, и, таким образом.

Это соотношение выражает тот факт, что кинетическая энергия жидкости, находящейся в вертикальном столбе (ширины d:!), равна потенциальной

энергии, измеряемой от невозмущенного уровня жидкости, заключенной в том же объеме. Этот результат верен только для волн, распространяющихся в одном направлении.

14.64. Изменение профиля в длинных волнах. Случай длинной волны, распространяющейся в одном направлении без изменения профиля, может быть сведен к установившемуся движению путем наложения на всю систему скорости, равной по величине, но противоположной по направлению скорости распространения волны с (рис. 278).

Рис. 278.

Тогда форма волны остается неизменной в пространстве и жидкость течет под ней с местной скоростью - c-f-a, где и - направленная вперед малая скорость в прогрессивной волне с возвышением т].

Тогда уравнение неразрывности принимает вид

(с-ы) (А-Ь'п)==сА,

откуда приближенно u=cr\/h; этот результат был получен уже ранее.

По указанной ранее причине (см. п. 14.60) вертикальная скорость мала по сравнению с величиной и, и, следовательно, квадрат ее есть величина четвертого порядка малости, если и -величина первого порядка малости; поэтому уравнение для давления на свободной поверхности примет вид

+ Yic-ur + gr\ = + cK

Исключая и с помощью уравнения неразрывности и пренебрегая кубом величины Tj/A, получаем соотношение

е - 2(h-bri)2 - 2А2

Условие существования установившегося движения состоит в том, что на свободной поверхности р = П. Таким образом, если величиной tjVA* нельзя

1) См. Stoker J. J., Соттип. Appl. Math., I (1948), 1 - 87. (См. цитированную монографию того же автора, стр. 390- 410.-Прим. перев.)

пренебречь, то свободная поверхность при c = gh не может существовать. Следовательно, длинная волна конечной высоты не может распространяться без изменения профиля.

Очевидно также, что если величиной ц^/Н^ нельзя пренебречь, то условию р = П можно приближенно удовлетворить, используя несколько большее значение скорости с, если величина ц положительна, и несколько меньшее значение, если величина т] отрицательна. Таким образом, возвышение стремится распространиться скорее, нежели понижение; волна стремится стать более крутой перед гребнем, и наблюдение показывает, что волна становится все более крутой и в конце концов разрушается*).

14.70. Действие малых возмущающих сил. Пусть X н Y обозначают горизонтальную и вертикальную компоненты малой возмущающей силы, действующей на жидкость, находящуюся в горизонтальном канале малой глубины ft, причем компонента X действует вдоль канала. Тогда уравнение движения принимает вид

ди Y I др dt--Jdx

Поскольку глубина мала, то практически величина Y постоянна при изменении от О до ft и, следовательно, величина Y очень незначительно изменяет величину g; действие этой составляющей будет величиной второго порядка малости. Таким образом, величиной Y можно пренебречь.

Тогда давление выражается формулой

p=Il + gQ {h + ц-у),

и, следовательно,

dt дх-

Если S обозначает горизонтальное перемещение частицы от ее невозмущенного положения, то имеем

уравнение неразрывности принимает вид

(ft-fTi) (dx + dx=hdx.

Оно выражает тот факт, что один и тот же объем жидкости заключен между плоскостями х и x + dx в возмущенном и невозмущенном положениях. Таким образом, имеем

л=-а|. (1)

и уравнение движения принимает вид

-Х4.с' (2)

Умножая это уравнение на величину -ft, дифференцируя по л; и используя формулу (1), получаем уравнение, определяющее изменение возвышения

= с2--л^ (3)

14.71. Приливы в экваториальном канале. Рассмотрим мелкий канал постоянной глубины, совпадающий с земным экватором, и предположим, что действур единственная приливообразующая сила, обусловленная Луной, движущейся ъ экваториальной плоскости.

Если через F обозначена напряженность лунного гравитационного поля, в центре Земли, то сила, приложенная к частицам жидкости в двух диаметрально противоположных точках экватора, будет равна F-f-f, F - f, где f - малое изменение F, если мы движемся от центра вдоль радиуса, длина которого мала по сравнению с расстоянием до Луны. Сила f представляет собой прилтообразующую силу, и вышеуказанное объяснение показывает, почему приливы образуются одновременно в противоположных точках Земли.

На рис. 279 изображен схематически экваториальный канал, где О - центр Земли, тИ -точка, расположенная непосредственно под Луной, G - точка пересечения нулевого Гринвичского меридиана с-экватором тл. Р - рассматриваемая точка, которая имеет долготу а.

Луна движется на запад относительно Земли с угловой скоростью п (предполагаемой постоянной) и в момент времени t угол GOM оказывается равным nt-\-R. Приливообразующая сила Луны, действующая на единицу массы, имеет в точке Р горизонтальную компоненту в направлении, указанном на схеме, равную /-sin (2 POMf).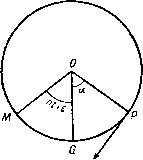

Рис. 279.

В случае Луны

для Солнца

/g=8,57xl0- ;

= 3,78Х 10- .

Если мы проведем через точку Р горизонтальную ось х, т. е. направим ее перпендикулярно отрезку ОР, и будем считать, что с увеличением х увеличивается и угол а, то будем иметь dx = ada, где а - радиус Земли. Таким образом, согласно формуле (3) п. 14.70, возвышение ц будет определяться уравнением

COS 2 (и^ -f- 8 -f а).

Полное решение этого уравнения можно рассматривать как сумму произвольного решения однородного уравнения и частного решения неоднородного уравнения. Первое слагаемое представляет собой свободные колебания жидкости малой амплитуды, которые быстро затухают под действием сил трения. Частное решение дает вынужденное колебание, которое является приливом. Для того чтобы найти частное решение, предположим теперь, что 1] = А cos 2 (nt + R -\- а); подставив его в уравнение, получаем

2(cz-я2а2) g

COS 2{nt + e + a).

Полагая a = 64 x 10 м, получим, что величина af/g равна 0,55 м в случае Луны и 0,24 м в случае Солнца. Отсюда следует, что мы получили полусуточ-

1) С подробностями читатель может ознакомиться в книге Ламба Гидродинамика , из которой взяты данные (см. также цитированную на стр. 409 монографию Л. Н. Сретенского, гл. IV и V. - Прим перев.).

ныи прилив, т. е. высокая и низкая вода имеет место дважды в течение лунного дня. Кроме того,

.- = 311-,

И так как /г/а для действительного океана малая величина, то разность -п^а^ будет отрицательной величиной и, следовательно, по этой теории прилив будет обращенный. Это означает, что низкая вода будет в точке, для которой Луна находится в зените, а также в диаметрально противоположной точке.

14.80. Трохоидальная волна Герстнера. В 1802 г. Герстнер, профессор математики в Праге, показал, что при специально выбранном трохоидальном профиле давление будет постоянно вдоль свободной поверхности глубокой, воды. Это единственное известное точное решение задачи о волновом движении. Однако это движение не является безвих-ревым!).

Направим ось х горизонтально, а ось у - вертикально вверх. Пусть а, b - параметры Лагранжа, определяющие положение отдельной частицы жидкости при отсутствии волн. Тогда волну Герстнера можно получить, если предположить, что положение этой частицы жидкости определяется формулами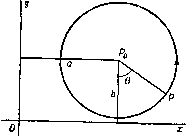

Рис. 280.

х = а + -е Чтт{а + Ы), у=Ь-

т

COS т {а+ ct).

Отсюда видно, что траекторией этой частицы является окружность с центром {а, Ь) и радиусом (рис. 280).

Угловая скорость радиуса, соединяющего частицу Р с центром Ро, равна тс.

Если мы будем рассматривать другие частицы, то в формулах (1) изменятся только значения а, Ь.

Для доказательства того, что формула (1) дает возможное движение жидкости, надо проверить, удовлетворяется ли уравнение неразрывности. Из формулы (1) мы имеем

z = a + /6 --ехр [т (Ь--/а + гс)]. (2)

Согласно п. 3.44, уравнение неразрывности принимает вид

дг д'г

const- = ----i?e ( I сопы - Э6 Эа И да дЬ

,2т Ь

Правая часть здесь является константой, так что движение возможно.

1) Обобщая теорию волн Герстнера, Л. Дюбрэйль-Жакотен [D и b г е i 1-J а с о t i п L.,. Sur la determination rigoureuse des ondes permanentes periodiques dampleur finie, J. math, pure et appl., XIII, № 3 (1934), 217--291] методом интегральных уравнений рассмотрела точное решение задачи о вихревых волнах на поверхности тяжелой жидкости как конечной, так и бесконечной глубины, считая интенсивность вихрей распределенной по показательному закону. Более обш,ее решение той же задачи, но другим методом дал Гуйон IGouyon R., Sur les houles planes en profondeur infinie, Compt. rend. Acad. Sci., 247, M 1 (1958), 33 - 35, № 2 (1958), 180-182, № 3 (1958), 266-269]. Существенное обобщение решения задачи о вихревых волнах дано в работе Моисеев Н. Н., Теоремы существования и неединственности вихревых волн периодического типа , Прикл. мат. и мех., 24, Ns 4 (1960), 711-714. Ему удалось построить решение, исходным приближением которого является некоторый вихревой поток, а не состояние покоя, как в других теориях. Задача сведена к некоторому нелинейному интегральному уравнению, к которому применимы хорошо разработанные в общей теории методы исследования.-Прйж. перев..

и затем сложим. Тогда получаем

(f + gri/) = тс е^ sin m (а + ct). (3)

Точно так же, складывая эти уравнения после их умножения на величины дх/дЬ, ду/дЬ, мы получим

§Ь (f+= - П' е cos т{а + ct) + тс с^ . (4)

Умножая уравнения (3) и (4) соответственно иа da н db и складывая результат, получаем

< (f+ ёГ) = < [ -ce cosm(a+cO+усе * ] .

и, следовательно,

= const - (6- е * cos m (а + сО ) - с* е * cos m (а + ct) + у с e *-

Для частицы, находящейся на свободной поверхности, величина р должна быть постоянной, если пренебречь поверхностным натяжением, и, следовательно, коэффициент при cos т (a + ct) должен обратиться в нуль, что приводит к равенству

= 1=Я|- (5)

т

Таким образом, условие на свободной поверхности удовлетворяется точно и давление в окрестности любой частицы жидкости с параметрами (а, Ь) выражается формулой

= const-bg + ce ,

и, следовательно, давление постоянно, если b постоянно. Это означает, что давление имеет постоянное значение для каждой данной частицы при ее движении. В частности, давление постоянно для всех частиц, для которых параметр b одинаков независимо от величины а.

Теперь следует получить условие на поверхности. Компонентами ускорения частицы являются dx/dt, dy/dt, и, следовательно, уравнейия движения принимают вид

а< 2 - Qdx dti~ S Q Qy

или

1 (f + gry ) = mce -sin m (fl+c/), S( + Sy)= -mc e cos m{a + ct). Умножим эти уравнения соответственно на следующие равенства: =l+e cosm (a + ct),

= e sinm(a + cO,

Если для частиц на свободной поверхности возьмем Ь=р, через П обозначим давление на свободной поверхности, то получим

Это соотношение определяет давление в любой другой точке. Согласно формуле (5), групповая скорость равна

14.81. Вид свободной поверхности. При исследовании вида кривых постоянного давления из уравнения (1) следует, что х vi. у являются периодическими функциями времени t, причем их период равен 2л/(тс).

Если сохранять величины but фиксированными, то значения у повторяются, когда а увеличивается на 2я/т, в то время как х получает линейный

Рис. 281.

сдвиг на величину 2я/т. Таким образом, наибольшего значения величина у достигает в точках, находящихся на расстоянии 2л/т. Рассматривая одно из этих наибольших значений у, мы видим, что с увеличением времени / требуется меньшее значение величины а, чтобы сохранить постоянным фазовый угол m (а + ct). Таким образом, профили поверхностей равного давления движутся в отрицательном направлении оси х со скоростью, равной частному от деления длины волны 2л/т на период 2л/(тс), т. е. со скоростью с. Если мы каждой частице сообщим скорость с противоположного направления, то движение станет установившимся и профили останутся неподвижными. Если написать Q = т {а-\- ct), то уравнение профилей поверхностей равного давления будет и*леть вид

x = l- + J-enbsine, / = 6--i-e cose.

Эти кривые являются трохоидами, которые описывает точка, находящаяся на расстоянии e ** /т от центра круга радиуса 1 /т, катящегося по нижней стороне линии г/ = 6 -f 1 /т (рис. 281).

Если на свободной поверхности 6 = О, то соответствующий профиль будет иметь вид циклоиды. Кривые равного давления изображены на рис. 282. Любая из них может быть взята в качестве профиля свободной поверхности. Предельная форма кривых - циклоида с остриями, направленными вверх в точках возврата. Вертикальные линии показывают невозмущенные положения столбов воды.

Чтобы найти средний уровень у = k, соответствующий любой трохоиде, т. е. уровень, относительно которого одинаковое количество жидкости как

возвышается, так и понижается, мы замечаем, что интеграл, взятый по длине волны (г/ - k) dx, равен нулю. Таким образом, имеем

5 (Ь-/г--1е со8в^ (l + e *cos9)d9=0,

что дает

gimb

Таким образом, средний уровень расположен ниже траектории центра производящего круга на величину е^ /2т.

При движении вниз расстояние рассматриваемой нами точки от центра производящего круга уменьшается.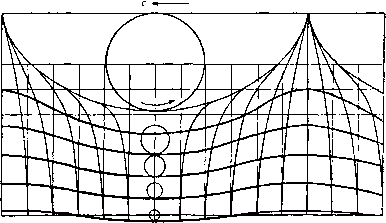

Рис. 282.

Для прогрессивной волны кинетическая энергия (приходящаяся на единицу толщины) находится интегрированием по длине волны кинетической энергии элементарной массы q (1 -е^ ) dadb, определяемой частицей жидкости (а, Ь). Из формул (1) и (2) п. 14.80 имеем

2 дгдг 2 2тЬ

Отсюда если для определения свободной поверхности положить Ь==р, то кинетическая энергия будет равна

2я

Положим к = 2п1т, /i = 2e P/m, так что /г -высота гребня над впадиной. Тогда получим формулу для кинетической энергии, приходящейся на длину волны, в виде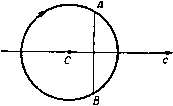

Что касается потенциальной энергии прогрессивной волны или установившегося обтекания профиля, то, считая средний уровень известной величиной и используя формулу (1), получим

Но из формулы (5) п. 14.80 следует g/m = с^, и поэтому

T=V.

Равенство Т = V мы будем использовать для того, чтобы дать интуитивную интерпретацию групповой скорости.

Частицы жидкости описывают окружности с постоянной скоростью, и давление в- окрестности частицы одинаково при любом ее положении на орбите. Рассмотрим теперь какую-либо частицу, орбита которой пересекает неподвижную вертикальную плоскость в точках А и В, как изображено на рис. 283. Поток кинетической энергии (или работа сил давления в единицу времени) через эту плоскость за один период равен нулю, так как то количество жидкости, которое перешло слева направо в точке Л, вернулось обратно справа налево в точке В. С другой стороны, поток потенциальной энергии не равен нулю, так Рис. 283. как потенциальная энергия, отнесенная к единице массы в точке А, превышает потенциальную энергию в точке В на величину g-AB. Ясно, что потенциальная энергия движется вместе с волной, т. е. со скоростью с. Но потенциальная энергия равна половине полной энергии. Следовательно, полная энергия переносится со скоростью ViC, т. е. с групповой скоростью.

Для доказательства того, что движение вихревое, заметим, что скалярное произведение скорости и радиуса-вектора и dx -\- v dy равняется действительной части от выражения (dz/dt) dz.

Из формулы (2) п. 14.80 имеем

dz = {c ехр т (il + id)} {dl+ dl exp m (- il - id)},

где / = a -f ib. Таким образом,

udx+vdy = d (-e s:nm {a + ct) + сеЫа.

Это выражение не является полным дифференциалом, и, следовательно, рассматриваемое движение вихревое. Циркуляция в элементарном параллелограмме жидкости получается из второго члена в правой части написанного выше выражения (так как первый член есть точный дифференциал) и поэтому равна

-(се2 Ьба)бй.

Разделив эту величину на площадь параллелограмма, получим интенсивность вихря

со =---- .

1 gimb

Огрицательный знак указывает на то, что вихрь имеет направление, противоположное вращению частиц по их круговым орбитам.

Интенсивность вихря быстро уменьшается с глубиной.

2= + ае Р. (3)

Тогда из формулы (4) п. 11.63 получим

Свободная поверхность, определяемая уравнением (3), есть трохоида без двойных точек, если амплитуда а < glw, причем длина волны равна

K = 2ngl(u. (5)

Таким образом, условие а < означает, что 2яа < %.

Скорость -dw/dz становится бесконечной, если dz/d = 0; это дает

о)Р = 2я( + )-Пп2, (6)

где л -любое целое число. Соответствующие значения г являются особыми точками

2 = Я

Такие особенности должны быть исключены из потока. Для осуществления этого можно взять в качестве дна линию тока, проходящую через особые точки или выше особых точек, задаваемых уравнением (7).

На рис. 284 (взятом из статьи Джона) изображена свободная поверхность и поверхность дна, образованная линией тока, проходящей через особые точки для различных значений отношения А = 2яаА. Единицы измерения на диаграмме выбраны так, что <в = = 1 и Я = 2л. При малых значениях отношения а/к глубина жидкости велика по сравнению с величиной а, величина К имеет порядок К\п (Я/а), а амплитуда поверхности дна является бесконечно малой величиной порядка а^/Я по сравнению с амплитудой свободной поверхности. С другой стороны, когда отношениеа/Я близко к величине 1/2я, глубина жидкости мала и поверхность дна имеет сходство со свободной поверхностью. При движении, описываемом формулами (3) и (4), свободная поверхность не изменяется со временем и каждая частица имеет горизонтальную скорость, наменяющуюся от {g/cd -аа) до (g/w аса).

Введем новую систему координат, движущуюся относительно старой вправо с постоянной горизонтальной скоростью /<в. Тогда мы получим дви-

14.82. Точное решение для безвихревой волны. Уравнение Джона (3) п. 11.63 можно применить также к волновому движению.

Рассмотрим установившееся движение, которое получится, если положить

5(Р) = ор, (1)

где <в - постоянная величина с размерностью \Т~]. Тогда имеем

2ф) = 5+ае* Р + гр/о), (2)

где без потери общности можно положить В = 0, а величину а считать действительной и положительной, так что