случае, если выполняется неравенство

mh = ~> 2,65.

Таким образом, воду можно, несомненно, рассматривать как глубокую, если глубина превышает половину длины волны.

Подводная лодка, расположенная на глубине, равной половине длины волны, почти не будет воспринимать движение воды, обусловленное поверхностными волнами.

14.18. Давление, обусловленное волной на глубокой воде. Если р - давление на частицу, среднее положение которой соответствует точке г, то уравнение давления имеет вид

f+giy+y)

= const.

Теперь, с одной стороны, величина gy равна мнимой части от выражения - agre- - ); с другой стороны, величина gy равна действительной части выражения /age- (mz-nO; кроме того, величина d(p/dt равна действительной части от выражения /аспе * - ). Отсюда заключаем, что dffldt - gy, так какс = д/т.

Таким образом, получаем уравнение p/Q-\- gy = const; иными словами, давление на любую частицу равно давлению в среднем положении этой частицы.

Рис. 266.

14.20. Кинетическая энергия прогрессивных волн. Кинетической энергией прогрессивной волны мы будем называть кинетическую энергию жидкости, отнесенную к единице толщины и заключенную между двумя

вертикальными плоскостями, помещенными на расстоянии длины волны друг от друга и перпендикулярными направлению распространения волны (рис. 266).

Проведем одну из плоскостей через ось у, тогда на основании п. 9.10 для жидкости, находящейся внутри контура, справедливо равенство

W dw.

(ОАВС)

В силу периодического характера движения ясно, что величина w имеет одно и то же значение в соответствующих точках линий АВ и ОС и, следовательно, вклад от этих линий в интеграл равен нулю. Таким образом, для прогрессивной волны п. 14.13 мы имеем

г = 1/е

1 . а^с^т

~ 8sh2mЛ

(sin2{tnx - nt) - ish2my)dz.

5р тЛ j cos(m2 -п/) sin (m2 - n/)d2 =

10A)+(BC)

(оа)+(вс)

Далее, вместо того чтобы интегрировать вдоль профиля волны ВС, мы можем интегрировать вдоль прямой линии ВС, так как возвышение мало. Таким образом, используя формулу (3) п. 14.13, находим

к

= - ¥ М 2mh dx=\ agQl.

14.21. Потенциальная энергия. Потенциальная энергия, отнесенная к единице толщины, обусловлена возвышением воды на интервале длины волны и, следовательно, отсчитывается от невозмущенного уровня; она вычисляется по формуле

\-n-8Qdx = agQ \2sin(mx - nt)dx = -aggk о b

и равна кинетической энергии.

Таким образом, полная энергия прогрессивной синусоидальной волны равна VzagQk на единицу длины, причем половина этой энергии является кинетической, а половина - потенциальной энергией, обусловленной возвышением жидкости над невозмущенным уровнем.

Можно также заметить, что средняя энергия, приходящаяся на единицу длины волны, равна /4a*gQ.

14.22. Групповая скорость. Местное возмущение поверхности спокойной воды создает волну, которую можно разложить на ряд простых гармонических компонент, каждая из которых имеет разную длину волны. Мы видели, что скорость распространения зависит от длины волны. Таким образом, волны различной длины постепенно разделяются на группы волн приблизительно одинаковой длины. В общем случае волн на воде групповая скорость меньше, чем скорость отдельных составляющих волн. В этом случае происходит следующее: передние волны выходят из группы, а новые волны сзади входят в группу. Энергия группы остается постоянной.

Для изучения свойств такой группы рассмотрим сначала частный случай возмущения, обусловленного наложением двух волн одинаковой амплитуды

Т1, = а sin {тх - nt), rja = а sin {{/и -)- дт) x - {n + bn)t},

где 6т, Ьп - бесконечно малые величины. Результирующее возмущение будет иметь вид

(\ = 2acos-2(xbm -tdn) sin (mx - nt) = А sin (mx - nt), (1)

где A=2a cos (x6m -t 6n). Следовательно, из уравнения (1) мы видим, что результат наложения двух волн можно рассматривать как прогрессивную волну с переменной амплитудой, которая изменяется как волна со скоростью Cg=bn/6m. Эта скорость называется групповой скоростью, для волн длины X она выражается в виде

dn d(mc) , dc .do

i dm dm dm dk

Используя значение скорости волны с, определяемое формулой (3) п. 14.13, мы получаем для одной группы простых гармонических волн следующее выражение для скорости:

Если mh=2nh/k велико, то групповая скорость равна Уз с. Таким образом, для волн на глубокой воде групповая скорость равна полсжине скорости волны. Если вода очень мелкая (Л/Я мало), то групповая скорость равна скорости волны.

В более общем случае местное возмущение, такое, как всплеск, будет порождать волны различной длины с малыми амплитудами а, Оь Oz, .... Если рассматривать только волны приблизительно одинаковой длины 2п/т, то возвышение на расстоянии х в момент времени t будет состоять из

суммы большого числа бесконечно малых членов; таким образом,

т] = а sin [тх - nt] + Oi sin [(т -г 8mi) х - (n + 6ni) / + + ... = - Л sin (тх - nt) + B cos {тх - nt) -С sin {тх - nt + г),

где

Л = a + Ci cos (л; 6mi - / 6ni -(- e,) + Сз cos (x б/Лз - if бпа + ег) + .. , fi = aisin{xbmi - tbni + ei) + a2sm{x6m2. - t8n2 + e2) + ...,

С2=Л2 + В2 Далее, имеем

x6mi - /бп1 -f ei = 6mi X - t+ei== bmi{x - ct)-f ,

Хб/Лз - tbn2 + 82 = fimz - Cgt) + 82, . . .

Следовательно, величины A, В, a значит, и величины Сие являются функциями от {х - Cgt). Таким образом, огибающая графика амплитуд движется как волна со скоростью с^ (рис. 267).

tg8 = T- .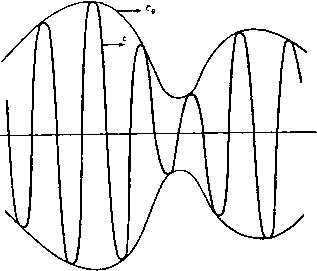

Рис. 267.

14.23, Динамический смысл групповой скорости. В простой системе гармонических волн энергия переносится через вертикальную плоскость, перпендикулярную направлению распространения волн, со средней скоростью, равной групповой скорости.

Доказательство. Пусть р - переменная часть давления и пусть и - горизонтальная скорость для фиксированного значения х; тогда работа сил давления, которая совершается в единицу времени и приложена к жидкости, находящейся справа от плоскости х, равна

= \ pudy.

Далее, поскольку р = е^, и равняется действительной части от выражения

dw опас . / j\ ,

sh mh - величина и равна действительной

*) Здесь, в пп. 14.30-14.34 приведена линейная теория бесконечно малых стоячих волн. Однако в литературе имеются исследования по теории стоячих волн конечной амплитуды, в которых находятся решения полных уравнений гидродинамики, удовлетворяющие нелинейным граничным условиям. При решении применяются ряды по степеням малого параметра и переменные Лагранжа; при этом в качестве первого члена берется данное решение линейной теории. Показано, что, удовлетворяя всем условиям, можно построить любое приближение, однако сходимость рядов не доказана. Установлен ряд свойств стоячей волны конечной амплитуды, отличающих ее от волны линейной теории. Основные результаты в этой теории получены Я. И. Секерж-Зеньковичем в его работах, опубликованных в 1947-1959 гг.; первая из них называется К теории стоячих волн конечной амплитуды на поверхности тяжелой жидкости , ДАН СССР, 8, № 4 (1947), 551-553. Темы многих последующих работ того же автора и других авторов можно найти в статье Вейхаузеиа (см. прим. перев. на стр. 409) и в вводной статье к сборнику переводов (указанных там же). Тот же автор рассмотрел конечные колебания поверхности раздела двух неограниченных жидкостей разных плотностей, расположенных одна над другой (см. ДАН СССР, 136. № 1 (1961), 51-59; Труды Морского гидрофизического института АН СССР, Х\Ш (mi), Ъ-43.-Прим. перев.

dw mac . , ,ч ,

части от выражения-sm (тх -nt)cntny, то имеем

соотношение

Среднее значение выражения sin (mx - nt) за период равно /г. Следовательно, средняя мощность определяется соотношением

acmriQ sh2mh f, , 2mA N аЧто ... 1 a

4ira -Эй- С1 + 1Ж-> -2- тЛс, = 2 gQac

в котором была использована формула (3) п. 14.13. Но величина V-igQa является энергией, отнесенной к единице длины волны. Таким образом, энергия переносится через плоскость со средней скоростью с^.

14.24. Волновое сопротивление. Твердое тело, такое, например, как корабль, движущийся по поверхности воды, оставляет за собой волновой след. Эти волны обладают энергией, которая уносится жидкостью и рассеивается. Эта энергия возникает за счет энергии движущегося тела, которое вследствие этого испытывает сопротивление i?. Если с - скорость тела и, следовательно, скорость волнового следа, то мощность, которая тратится на преодоление сопротивления равна Rc. Если мы рассмотрим неподвижную плоскость, проведенную в нижнем бьефе потока (движение считается двумерным), перпендикулярно направлению движения тела, то скорость, с которой длина волнового следа увеличивается впереди этой плоскости, равна с, а, следовательно, скорость возрастания энергии впереди плоскости равна c-VigQcl, где а - амплитуда. Но мы знаем, что энергия переносится через неподвижную плоскость со скоростью, равной групповой скорости. Таким образом, получаем

c-\ga = Cg-\gQa-Rc,

и, следовательно,

если 2л п - длина волны, ah - глубина жидкости (см. п. 14.22).

Так как скорость распространения волн не может превышать величину

критической скорости, равной Ygh, то, следовательно, если тело имеет скорость, большую критической скорости, то никакой волновой след не будет сопровождать тело и волновое сопротивление будет равно нулю. Это обстоятельство хорошо подтверждается наблюдениями.

14.30. Стоячие, или стационарные волны*). Две системы простых гармонических волн равной амплитуды, распространяющиеся в противоположных

направлениях, заданы следующими законами изменения возвышений свободной поверхности:

т]! = а sin {тх - nt), f]2 = -(i sin {тх +nt).

В результате наложения этих волн получаем закон изменения возвышения вида

т| = а sin тх cos nt.

Движение такого типа называется стоячей, или стационарной, волной. При данном фиксированном значении х поверхность воды движется вверх и вниз. В данный момент времени t форма поверхности представляет собой синусоидальную кривую с амплитудой а cos nt, изменяющейся, следовательно, от О до а. Волна такого типа не перемещается в пространстве.

Точки, в которых mx = sn, где s= . . ., -2, -1, О, 1, 2 . . ., всегда неподвижны на средней поверхности уровня и называются узлами. Точки, в которых тх = (2s+1) п/2, являются точками максимального перемещения для данного значения t и называются пучностями. Если cos ± 1, то поверхность имеет форму синусоидальной кривой r\=±asinmx, представляющей максимальное отклонение свободной поверхности от среднего уровня. Когда cos nt=0, свободная поверхность совпадает с плоскостью среднего уровня.

Если ряд прогрессивных волн, представляемых функцией t)i, ударяется о вертикальную стенку и отражается от нее (ria), то результирующее возмущение после достижения установившейся стадии состоит из стоячих волн.

Такие волны, например, могут быть вызваны легким наклоном прямоугольного сосуда, содержащего воду, и возвращением его в прежнее положение. Уровень воды на краях сосуда движется вверх и вниз вдоль вертикальных стенок, которые являются пучностями. И обратно, прогрессивную волну можно рассматривать как волну, образованную наложением двух стоячих волн.

14.31. Комплексный потенциал стоячих волн. Для получения стоячих волн мы можем подставить в формулу (5) п. 14.13 соответствующую гармоническую по времени функцию для w. Положив

w{z, t) = Asin mz sin nt,

мы получим

w{z + ih, t) + w{z - ih, t) - 2A sin mz ch mh sin nt, w{z + ih, t) - w{z~ih, t) = 2iA cos mz sh mh sin nt.

После подстановки в указанную формулу мы получим n=mgthmh. Это уравнение связывает частоту с длиной волны. Поверхностное возвышение gt] равно действительной части от выражения (2) п. 14.12,

gr = Re = Лл sin тх ch mh cos nt.

Следовательно, если возвышение равно ti = а sin тх cos nt, то мы получаем

а = An ch mh/g = Am sh mh/n,

так что

ас . , n

t =-r-г sin mz Sin nr, c = - . sh mft m

Этот результат можно получить сразу путем наложения двух решений вида, найденного в п. 14.13; в этом случае имеем

ш= ycccsch mh cos {mz-nt)- ас csch mh cos {mz + nt).

14.32. Траектории частиц в стоячей волне. Будем использовать метод, изложенный в п. 14.15. Пусть z+z- смещенное положение частицы в момент времени t, пусть г - среднее положение частицы. Тогда получаем

dz dw аст

sh mh

sh mh COS mz cos nt.

cos mz sin nt,

Таким образом, arg 2 является постоянной величиной и, следовательно, частицы совершают простое гармоническое движение периода 2п/п, равное периоду волны. Амплитуда этого движения равна

I у (cos 2тх + ch 2ту) ]

sh mh

COS mz =

sh mh

Таким образом, амплитуда уменьшается при перемещении вниз по поверхности. Наклон линии, соответствующей среднему положению г, равен

arg 2 = arg COS mz = arctg {tg mx th my).

Сдедовательно, этот наклон равен нулю для узлов (тх = sn) н У2П - для пучностей. Таким образом, под узлами частицы движутся горизонтально, под пучностями они движутся вертикально (рис. 268).

Рис. 268.

Рис. 269.

14.33. Стоячие волны в прямоугольном бассейне. Так как движение под пучностями в стоячих волнах вертикальное, то движение между двумя данными пучностями не изменится, если в них поместить две неподвижные твердые вертикальные плоскости. Тогда мы получим случай жидкости, колеблющейся в бассейне конечных размеров.

Рассмотрим прямоугольный бассейн длины /. Поместим начало координат на дне у стенки бассейна и ось у направим вертикально вверх. Так как при x = О мы имеем пучность, то возмущенная поверхность должна иметь вид

Ti = acos тх cos nt,

и отсюда

w = ac cos mz sin n sh mh. Так как при x = / также должна быть пучность, то мы получим

ml = sn,

где S - любое целое число. Таким образом, возможные длины волн при колебании принимают значения

к = 21, I, 2 3, 2 4, ....

Если фотографическую пластинку проявлять, покачивая ванночку, содержащую проявляющий раствор, то надо позаботиться о том, чтобы изменять

(/>=-cb

Рис. 270.

вместе с волной, то комплексный потенциал можно получить путем замены величины г суммой z+ct; тогда комплексный потенциал принимает вид <рис. 270)

ас cos тг shmft

Если всей системе придать скорость с в направлении отрицательной оси х, то оси координат и волновой профиль останутся неподвижными, а жидкость будет иметь общую скорость с, направленную справа налево, причем комплексный потенциал теперь имеет вид

sh mh

Эта измененная формула комплексного потенциала соответствует установившемуся движению, при котором сила, действующая на любую частицу, не изменяется, так как добавление постоянной скорости не оказывает динамического

*) В линейной теории установившихся волн на поверхности жидкости бесконечной глубины весьма плодотворен метод М. В. Келдыша (см. Технич. заметки ЦАГИ, № 52, 1935), основанный на применении аналитической функции F (г) = dwIdz + giw/c (см. также прим. перев. на стр. 409).- Прим. перев.

частоту колебаний, иначе части пластинки, расположенные ниже пучности волны, недопроявятся, так как раствор вблизи этих точек имеет очень незначительное движение и химическое действие раствора вскоре прекратится, что приведет к образованию полос на фотопластинке.

14.34. Энергия стоячих волн. Рассмотрим слой единичной толщины; потенциальная энергия этого слоя на интервале длины волны задается формулой

г, о

Если возьмем т) = а sin тл; cos nt, то получим gQO cos nt к, и если

cosn/=l, то потенциальная энергия равна /igqak.

В рассматриваемый момент времени вся энергия является потенциальной, так как кинетическая энергия зависит от скорости, нормальной к границе (см. п. 3.72), которая равна нулю. Кинетическая энергия стоячей волны в момент времени / равна Т = 4igQasinnt-к.

14.40. Установивщееся движение*). Комплексный потенциал для простой синусоидальной волны, движущейся вперед, был получен в виде уравнения (3) п. 14.11. Если мы будем рассматривать оси координат, движущиеся

Ho с принятой точностью поверхность является линией токаф=0, так что, пренебрегая величиной т]*, получаем формулу

r\ - as\nmx. (2)

В случае глубокой воды комплексный потенциал принимает вид

wcz + ace- , (3)

поэтому для линии тока на поверхности, гдеф=0, имеем

т] = аеп sin тх, (4)

что соответствует формуле (2) с принятой точностью.

14.41. Второе приближение для величины скорости волны. Рассмотрим для простоты случай глубокой воды; в этом случае комплексный потенциал и профиль поверхности задаются формулами (3) и (4) п. 14.40. Замечаем, что формула (4) получается из равенства (3), если в нем положить ф = О, но при этом не предполагается, что формула (4) обязательно соответствует поверхности постоянного давления. Для квадрата модуля скорости имеем формулу

д^ = = сЦ1-imae ) (1 + /тае^ ) = = с2 (1 -2ате' sin тл;+а'т^ ). Отсюда на свободной поверхности находим соотношение = 1 - 2тт] -г а^/п^е^ } = с^* {1 - 2тт1 + а^т^ (1 -f 2тт1 -f 2т\ +)}

Если р - давление в жидкости на свободной поверхности, а П - внешнее давление, то уравнение для давления теперь имеет вид

р - n = Q( - g-T]-)-тт]с2 - с'а^т\ - damf - ...}-f const =

= РЛ{-+c/n--c2a2m} -QcaSV - ... +const. (1)

Если в этих формулах пренебречь членами, содержащими а^, то получим р=П, если с* = gim; этот результат был уже получен ранее. Более точное равенство величин р и П получим, если пренебрежем членами, содержащими а^т*г\, которые являются величинами четвертого и более высокого порядка малости. В результате этого свободная поверхность будет поверхностью

воздействия. Проведенная замена переменных удобна тем, что в новой системе отсчета профиль волны теперь является линией тока, соответствующей постоянному значению ф. В приложениях обычно удобнее начало координат брать на невозмущенной поверхности, следовательно, надо написать 2 +/Л вместо г'. Таким образом, окончательно, опуская постоянную cih, получим комплексный потенциал в виде

Дно теперь является также линией тока

ф= -ch,

в то время как на свободной поверхности имеем

ф = ст] - sh m (т] + h) sin mx = ct\ = ас (ch тц -f sh тц cth mh) sin mx.

где были опущены члены четвертого порядка малости. Полученное соотношение является более точным приближением для скорости волны. Заметим, что скорость, найденная таким образом, зависит не только от длины волны, но также и от амплитуды.

Максимальная величина первого члена, которым мы пренебрегали в формуле (1), а именно - QCatn4\, равна - 2gQa (aW/2), эта величина является правильной дробью от выражения а'т'/2- разности давления между гребнем и впадиной. Таким образом, для волны с амплитудой 4 фута и длиной 80 футов эта дробь равна

Следовательно, давление, которым мы пренебрегаем, самое большее равно 0,03456 м вод. ст.

14.42. Волны на поверхности раздела. Рассмотрим жидкость, плотности q и глубины h, текущую с постоянной скоростью V, по слою жидкости

Рис. 271.

плотности Q и глубины h, текущей с постоянной скоростью V, причем жидкости сверху и снизу ограничены твердыми горизонтальными плоскостями.

Поместим ось х вдоль (геометрической) поверхности раздела, которая отделяет жидкости и составляет вихревой слой. Для исследования того факта, что волны малого возвышения 1] = а sin (тх - nt), могут распространяться по поверхности раздела со скоростью с - п/т, придадим всей массе жидкости скорость с, противоположную направлению распространения; таким образом, профиль волны станет неподвижным, а скорости потоков относительно профиля будут равны V - с aV - c (рис. 271). Из п. 14.40 следует, что комплексный потенциал для нижнего слоя жидкости имеет вид

ш= -(V-c)z- -cosm(z + ih), (1)

тогда линией тока ф = 0 является синусоида т] = а sinmx.

Отсюда сразу получим выражение потенциала для верхнего слоя жидкости, написав -h вместо /г; в результате получим

да = (У с) Z + cos m(z- ih). (2)

постоянного давления, если - g-b с*т - c*aW = О, откуда получаем с2 = (1 -aW)- = -- (1 +

4 Я'Я? -ЯЯ1 + g4 iQ -Q) = const.

Подставив сюда значения qo и q , мы должны будем потребовать, чтобы коэффициент при т) в полученном выражении обращался в нуль, следовательно, находим уравнение

mq (У - су cth mh + mQ {V -с) cth mh = g{Q-Q).

Это уравнение определяет скорость распространения волн. Сделаем следующие замечания:

(i) Если q = о, v = О, то уравнение сводится к формуле (3) п. 14.13.

(ii) Если обе жидкости имеют бесконечную глубину, то уравнение упрощается и принимает вид

mq (V -с)2 + mq {V -cy = g{Q-Q).

(iii) Условие устойчивости свидетельствует о том, что волны рассматриваемого типа могут распространяться, т. е. величина с будет действительной.

(IV) В общем случае уравнению удовлетворяют два значения величины с.

(v) Если с = о, то волна стоячая.

(vi) Если обе жидкости покоятся, за исключением волнового движения, то V = V = 0; если при этом глубина каждой жидкости бесконечна, то

g (.Q- Q) m(Q+Q)

Отсюда следует, что должно быть выполнено условие q > q, т. е. более тяжелая жидкость должна располагаться внизу (см. п. 14.54). В частности, предположим, что верхняя жидкость представляет собой воздух бесконечной глубины с удельным весом s. Тогда, полагая V=V=0, получаем приближенно

с2 = X jfc!L А th m/i {1 - S (1-Ь th тЛ)},

так как величина s мала. Сравнивая это выражение с формулой (3) п. 14.13, мы видим, что наличие атмосферы стремится уменьшить скорость волны.

Пренебрегая величиной а* для скорости в нижнем слое, получаем формулу

следовательно, на поверхности раздела скорость выражается в виде

ql{V-cY{\-2mx[ cthmA},

а для верхнего слоя жидкости скорость на той же поверхности равна

q = {V-cf{\ -f 2/nTicth mh}.

Теперь на поверхности раздела уравнение давления для обеих жидкостей записывается в виде

p + yQ7; + qgril = const, (3)

P + yQ<7o + Q=const. (4)

Но давление должно быть непрерывно и, следовательно, р = р'. После почленного вычитания уравнений (3) и (4) получим