Примеры

цилиндра и вихрь. Указать, каким способом можно вычислить суммарное давление жидкости на цилиндр.

12. Неподвижный цилиндр радиуса а окружен безграничной идеальной несжимаемой жидкостью. В жидкости имеется вихрь интенсивности т, ось которого параллельна оси цилиндра и который отстоит от оси цилиндра на расстоянии с(с>а). Считая, что циркуляция по любому контуру, охватывающему цилиндр, но не охватывающему вихрь, равна нулю, показать, что скорость жидкости q на поверхности цилиндра равна

m / £2-0*4

где г-расстояние рассматриваемой точки от вихревой нити. Показать далее, что давление на поверхности цилиндра

где Ро-давление на бесконечности.

13. Прямолинейный вихрь находится в однородной идеальной несжимаемой жидкости, заключенной между двумя соосными прямыми круговыми цилиндрами, образующие которых параллельны вихрю. Радиусы цилиндров равны и rj, расстояние вихря от оси цилиндров равно с. Найти функцию тока течения и показать, что при crri вихрь будет покоиться; в противном же случае траекторией вихря будет окружность.

14. Неподвижный круговой цилиндр обтекается равномерным потоком идеальной несжимаемой жидкости, скорость которого на бесконечности равна I и направлена вдоль оси X. Движение жидкости считается плоским, начало системы координат выбрано в центре поперечного сечения цилиндра О. За цилиидром имеется пара вихрей, расположенных симметрично относительно оси х. Доказать, что вихри будут неподвижны относительно цилиндра, если они лежат на кривой

и что интенсивность вихрей в этом случае равна

где г-расстояние от точки О. Установить без доказательства, будет ли эта система устойчивой или нет, коротко объяснить связь этого теоретического результата с течением, наблюдаемым при обтекании кругового цилиндра жидкостью с малой вязкостью.

15. Вихревые нити интенсивности Xj, X21 параллельны оси Oz, пересекают плоскость г=0 в точках (xi, yi), (Х2, (/2). Доказать, что

ЩХ1=А, 2xii/j = B, щг\ = С, 2<iiei = 2n ХгХ;-

Пусть пара вихревых нитей, интенсивности которых равны по величине, но противоположны по знаку, расположена внутри или вне кругового цилиндра радиуса а на одинаковом расстоянии от оси цилиндра. Доказать, что уравнение цилиндра, описываемого каждым из вихрей, есть

(г*-а2)2 (г* sin е - 62) = 4а.ЧV* sin* в,

где b - некоторая постоянная.

16. Вихрь интенсивности х расположен в точке S = td вне окружности = с. Применить конформное преобразование iz=Z,-\-c/t, для определения комплексного потенциала течения от вихря в точке z=f около плоской пластины длины 4с, на которую наложена циркуляция 2я5* (А,- 1). Показать, что для того чтобы скорость вихря обратилась в нуль, необходимо, чтобы X, = (d*-l-c*)/(d*-с*), а для того, чтобы скорость на конце пластины была конечной, необходимо, чтобы X = (d - c)/{d-\-c), т. е. показать, что скорость на конце пластины не может быть конечной, если вихрь находится в покое. Величины d и f считать действительными.

17. Три вихревые нити, каждая интенсивности т, симметрично расположены внутри неподвижного кругового цилиндра радиуса а. Вихри проходят через вершины равностороннего треугольника со стороной YZb. Считая, что в отсутствие этих вихрей циркуляция в жидкости равна нулю, показать, что вихри будут вращаться вокруг оси цилиндра с угловой скоростью

bi I о -Ьв

18. Показать, что бесконечный жидкий цилиндр, поперечное сечение которого является эллипсом и внутри которого вектор вихря g постоянен и параллелен образующей, может сохранять свою форму, если он вращается как твердое тело (центр поперечного сечения неподвижен) с угловой скоростью = A,g, где параметр X, зависит только от эксцентриситета поперечного сечения.

где через обозначена величина, комплексно сопряженная с о. Показать, что такая цепочка вихрей неустойчива.

Найти траектории жидких частиц внутри цилиндра: 1) относительно вращающегося поперечного сечения, 2) относительно неподвижной системы координат.

19. Доказать, что цилиндрический вихрь постоянной интенсивности, поперечным сечением которого является эллипс с полуосями а и 6, может существовать в несжимаемой идеальной жидкости постоянной плотности q и постоянного давления Р на бесконечности при условии, что этот вихрь вращается вокруг своей оси с некоторой определенной постоянной угловой скоростью п.

Показать, что на концах малой полуоси возникает кавитация, если не выполняется условие Я > qrt2 (а-(-6) а, и что при отсутствии кавитации линии тока в относительном движении жидкости совпадают с линиями постоянного давления внутри вихря.

20. Показать, что при установившемся плоском движении жидкости с постоянной завихренностью имеет место равенство

Доказать, что при = 0 суммарная сила давления равномерного потока со скоростью V на неподвижный цилиндр с произвольным поперечным сечением равна xqV и действует под прямым углом к направлению потока. Через х здесь обозначена циркуляция по любому контуру, охватывающему цилиндр.

Найти вид функции tJ;, если £=50, а цилиндр круговой. Показать, что если движение жидкости на бесконечности представляет собой поступательный поток, параллельный оси Ох, то предыдущий результат справедлив при условии, что в формуле величина к заменяется на x-fna, где х'-циркуляция на поверхности цилиндра, а V-скорость в бесконечно удаленной точке на линии тока, проходящей через центр цилиндра.

21. В безграничной жидкости имеется бесконечная цепочка прямолинейных вихрей расположенных на одинаковом расстоянии а друг от друга. Величина интенсивности каждого вихря равна х, а знак интенсивности чередуется от вихря к вихрю. Пусть начало координат совпадает с одним из вихрей положительной интенсивности. Показать, что комплексный потенциал течения имеет вид

и, следовательно, такая цепочка вихрей не движется.

Показать, далее, что если радиус поперечного сечения каждой вихревой нити равен га, где е -бесконечно малая величина, то расход жидкости между двумя сосед-

ними вихрями равен приближенно 2х In - .

22. Показать, что комплексный потенциал w бесконечной цепочки вихрей интенсивности x, расположенных в точках с координатами

Zr = ra, (г=0, ±1, ±2,...),

задается формулой

ш = 1х In sin - .

а

Пусть вихри в цепочке получили малые смещения, так что Zr = ra-\-(l-\-ir\)e , (0<а<2л). Показать, что со временем смещения вихрей возрастают как е^, где

, ха(2я-а) 22

23. Бесконечная цепочка состоит из вихрей интенсивности т, расположенных в точках г = го-\-па, где п-любое положительное или отрицательное целое число ил нуль. Показать, что скорость (и, v), индуцированная этой цепочкой в точке г, равна

. . irrm , я(2-Zo)

- u-l-(tl =- ctg -i-- .

a a

Пусть теперь вихри в цепочке получили малые смещения

tn = ?ocos nx,

где 0<Х<2я. Получить уравнение движения вихря в виде

24. Показать, что функция тока бесконечной цепочки прямолинейных вихрей одинаковой интенсивности х, равномерно с интервалом о распределенных на оси х в безграничной жидкости, Задается формулой

1=-2-1п

, 2яу 2ях

ch--cos-

а а

я5* /с

Следует иметь в виду, что вихри параллельны оси г.

Пусть вторая цепочка вихрей -ч получена сдвигом первой цепочки как целого на х=Ха, у--]1а. Показать, что такая двойная цепочка вихрей, или вихревая дорожка, движется со скоростью

сЬ2яцЧ-соз 2яХ\Уг .ch 2я(*-соз2яХу в направлении, составляющем с дорожкой угол 6, причем

25. Две параллельные цепочки состоят из вихрей, расположенных равномерно с интервалом а, и отстоят друг от друга на расстоянии Ь. Все вихри одной цепочки имеют одииаковую интенсивность К, а все вихри другой-интенсивность -К. Найти условия, при которых цепочки будут двигаться вперед с постоянной скоростью, и определить эту скорость. Показать, что система будет неустойчива, если вихри одной цепочки расположены точно под вихрями другой цепочки. 26. Задана бесконечная вихревая дорожка:

х=га, у=Ь, интенсивность каждого вихря т;

х = га, у=-Ь, интенсивность каждого вихря-т; где л-любое положительное или отрицательное целое число или нуль. Показать, что если жидкость на бесконечности покоится, то вихревая дорожка движется как целое, вдоль оси X со скоростью

ят 2яй - cth--.

а а

Показать, что такая дорожка неустойчива по отношению к малому смещению одного вихря.

27. Вычислить скорость вихревой дорожки Кармана, состоящей из цепочки вихрей интенсивности т и цепочки вихрей интенсивности - т; вихри одной цепочки чередуются с вихрями другой цепочки.

Пусть все вихри системы, кроме одного, не меняют своего взаимного расположения. Исследовать устойчивость движения этого вихря и показать, что оно не может быть устойчивым, если не выполняется некоторое соотношение между параметрами, характеризующими взаимное расположение вихрей в дорожке. Найти это соотношение.

Глава 14 ВОЛНЫ

14.10. Волновое движение. Волновым движением жидкости, находящейся под действием силы тяжести и имеющей свободную поверхность, называется движение, при котором возвышение свободной поверхности над некоторой выбранной фиксированной горизонтальной плоскостью изменяется.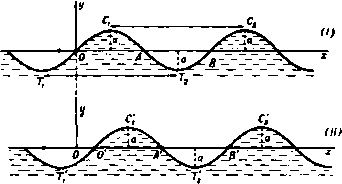

Р шс 261.

Если направить ось х горизонтально, а ось у вертикально вверх, то движение, при котором уравнение вертикального сечения свободной поверхности в момент времени t имеет внд

y = a%\n(mx - nt), (1)

где а, т, п - постоянные величины, называется простой гармонический прогрессивной волной.

Если нарисовать профи.1ь свободной поверхности (1) в момент ( = О, то получим синусоидальную кривую = а sin тх, изображенную на рис. 261 (/). Так как уравнение (1) может быть записано в форме

y = asinm(x-~. (2)

то мы видим, что профиль в момент времени / имеет тот же вид, что и в .момент t = О относительно системы координат, начало которой перенесено в точку О', где 00 = nt/m - отрезок, на который сдвинут профиль первоначальной формы (см. рис. 261 ( ))

Рис. 262.

И ось X направлена вдоль дна') в направлении распространения волны. Тогда уравнение свободной поверхности будет иметь вид у - i] - h О, но так

) Мы рассматриваем за.1ачу только для случая постоянной глубины Задачу для случая переменной глубины читатель может найти в работе Stoker ,(, J., Surface waves inwater of variable depth, Quart J Appl. Math., 5 (1947). 15. (Задачу для случая переменной глубины и волнистого дна можно найти также в монографии Дж. Дж Стокера (см. прим. перев. на стр. 409), п монографии Л. Н. Сретенского п в сборнике переводов (см. там же). Прим. перев.)

Следовательно, уравнение (1) характеризует движение, при котором кривая

(/ = а sin m.Y

движется в положительном направлении оси д: со скоростью с= т, называс-MOii скоростью распространении волны. Если положить а = О, то получим ;/ = О-прямолинейный профиль жидкости, являющийся ее средним уртне.ч.

Величина а называется а.шишпудой волны, она измеряет максимальное отклонение действительной свободной поверхности от среднего уровня. Точки

С], Сп.....максимальные возвышения свободной поверхности, называются

гребнями: точки Tt, Т2, .... максимальные понижения свободной поверхности, называются впадинами волны. Расстояние между двумя последовательными гребнями называется д.шной во.1ны к. Таким образом, имеем

т

Форма свободной поверхности одинакова в моменты времени / и /-f 2л/л. Промежуток времени

т -2-1 п

называется периодом волны. Величина, обратная периоду, называется частотой п12п. Угол т.х - nt называется фазовым углом, а число п обычно называют фазовой скоростью.

Введенные здесь величины связаны соотношением Х = ст. Уравнение профиля волны также может быть записано в виде

j/ = asin(.v- ci).

Заметим, что уравнение (1) характеризует двумерное движение. В этой главе мы будем рассматривать только двумерные (плоские) волновые движения, которые можно представить как движения жидкости между двумя вертикальными плоскостями, расположенными на единичном расстоянии друг от друга (см. рис. 261 ( /)). В дальнейшем движение всегда будет считаться двумерным, если нет других указаний.

14.11. Кинематическое условие на свободной поверхности. Рассмотрим слой воды глубины /I, в котором распространяются волны высоты у\ = г\ (.v. t) над средним уровнем, причем высота измеряется от невозмущенного уровня

) Из тех же соображевий линейности следует, что указанное условие должно быть выполнено вдоль плоскости y=h.- Прим. ред.

как поверхность движется вместе с жидкостью, то d {y - i\ - h)ldt = 0 (рис. 262); отсюда имеем:

Мы будем в дальнейшем рассматривать линейную теорию (если явно не указано противоположное), согласно которой .можно пренебречь квадратами и произведениями всех величин и их производных. В частности, величина дг]/дх, измеряющая наклон профиля волны, будет считаться малой. Тогда на свободной поверхности мы получим равенство

dt дх

где ф - функция тока*). Полученное равенство представляет собой кинематическое условие на свободной поверхности для волновых профилей малой высоты и наклона.

Из уравнения (1) следует, что в случае безвихревых волн, имеющих профиль

1\ = а sin (mx-nt), (2)

функция тока ф при y = h пропорциональна величине sin (mx - nt). На этом основании попытаемся найти решение уравнения (1) в виде комплексного потенциала w = b cos (mz - nt).

Тогда на свободной поверхности получим ф = - ftsin (тх - п1) sh mA при нашей степени приближения. Подстановка этой величины в уравнение (1) приводит к равенству

Ьт sh mh = an,

так что

где с = л/т - скорость распространения волны.

Следует заметить, что не было сделано никаких предположений относительно условий, которые имеют место выше профиля волны, следовательно, формула (3) справедлива в том случае, если профиль является поверхностью раздела между двумя жидкостями.

14.12. Условие для давления на свободной поверхности. Пусть pi - давление внутри жидкости в точке Р (см. рис. 262) и пусть ро -внешнее давление. Мы снова будем предполагать, что движение безвихревое; это предположение выполняется в случае волн, имеющих место в невязкой жидкости. Тогда уравнение для давления (если пренебречь членом Vz*) запишется в виде

P = Q(4r- Л)+С(0.

Слагаемое С (/) можно брать независимым от /, а зависящие от времени величины можно включить в член дф/д/. Таким образом,

Pi-Po=Q(f-gVi-Ро-\-const.

В случае постоянного (атмосферного) давления с помощью подходящего выбора функции ф мы можем написать

Pi-Po = Q(-gy)). (1)

В связи с этим заметим, что давления pt и ро могут отличаться друг от друга только на малую величину и, следовательно, d((/dt должно быть мало. Таким образом, уравнение (1) представляет собой условие для давления на свободной поверхности в случае безвихревых волн малой высоты.

Если пренебречь поверхностным натяжением (см. п. 14.50), то получим Рг - Ро = О и. следовательно,

Далее, на свободной поверхности имеем

Ф = Ф(х, л+т 0 = ф{. Л, о+л(-%),+ .-.

Следовательно, в вышеуказанном условии на свободной поверхности мы можем во втором члене принять у = h, иными словами, условие на свободной поверхности мы будем писать в форме

ёЧ=Щ^ (2)

Заметим, что уравнение (2) позволяет определить величину возвышения поверхности, если величина ф известна.

14.13. Поверхностные волны. Комбинируя кинематическое граничное условие (1) п. 14.11 с граничным условием для давления (2) п. 14.12, получаем

$- 1 = 0, yh. (I)

Далее, из п. 14.11 в случае простой гармонической прогрессивной волны (см. рис. 262) имеем

W - COS [mz - nt), x[=as\n{mx - nt). (2)

Таким образом, после простых вычислений из уравнения (1) получим уравнение, определяющее скорость распространения волны длиной 2п/т, в следующем виде:

c2 = -thmA. (3)

Уравнения (2) и (3) полностью характеризуют эти волны на поверхности воды глубиной h. Примечательно, что, в то время как уравнение (2) выводится только из кинематических соображений, уравнение (3) устанавливает соотношение между величинами п и т{с - nlrri), для того чтобы решение было физически удовлетворительным. Скорость распространения в действительности является функцией длины волны.

В более общем случае соответствующими условиями должны быть условие (1) и условие

ф = 0 при = 0, (4)

так как через донную часть границы поток отсутствует. Комплексный потенциал имеет вид

w==w{x-\-iy, t)=:({x, у, t)i{x, у, t).

Поэтому из условия (4) следует, что функция а) действительна, когда = 0. Следовательно, аналитическая функция w может быть продолжена по принципу симметрии (п. 5.53) в область, для которой у отрицательно, точнее, в полосу -Л< у < 0. Таким образом,

w{x~iy, t) = (fiXr у, О -Ф(. У, t).

следовательно, получим

ф(х, tf, t){w{x-iriy, t) + w{x - iy, t)],

г|з(х, у, t) = -i[w{x + iy, t) - w{x-iy, t)].

Полагая здесь у = h и подставляя результат в условие (1), мы получаем уравнение

[w(x+ih, t) + w(x-ih, t)] + ig-llo>(x + ih, t)-w{x-ih, /)] = 0.

Так как w - аналитическая функция, то это уравнение должно иметь место для любой точки в области существования этой функции. Таким образом, мы можш написать г вместо х и получить уравнение

-[w{z + ih, t) + w{z-ih, t)] + ig-llw{z + ih, t)-w{z-ih, 1 = 0. (5) Это уравнение впервые получил Чизотти

Отсюда следует, что любая аналитическая функция w (z, i), действительная на действительной оси, т. е. действительная при действительном z и удовлетворяющая уравнению (5), является комплексным потенциалом для бесконечно малого движения воды глубины h. Граничные условия (1) и (4) удовлетворяются автоматически.

Читатель может убедиться, что путем подстановки комплексного потенциала (2) в уравнение (5) получается условие (3). Таким образом, уравнение Чизотти полностью описывает волны указанного типа.

14.14. Скорость распространения. Скорость распространения, выраженная через длину волны к = 2л/т, задается формулой (3), п. 14.13 в виде

с Х 2nh

Если отношение Klh мало, то отношение 2nh/k велико и, следовательно, приближенно c/gh = k/2nh, так как th б -> 1 при 9 - -оо. Таким образом, для малых значений X/h скорость с пропорциональна Y- С другой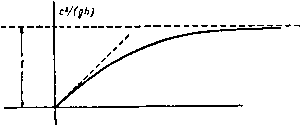

A/(2tTh}

Рис. 263.

стороны, если отношение k/h велико, то отношение А/Я мало и, следовательно, приближенно с =gA, так что скорость распространения стремится к постоянному значению Ygh, которое она не может превзойти. Эти результаты изображены графически на рис. 263, из которого видно, что данному значению с < У (gh) соответствует только одна длина волны

1) С i s о t t i. Rend. Lincei, (6), 29 (1920). [См. также монографию Л. Н. Сретенского, § 55 (прим. переэ. на стр. 409).- Прим.. перев.]

И ЧТО каждое такое значение является скоростью распространения некоторой волны. Результаты значительно изменяются из-за влияния поверхностного натяжения (см. п. 14.54).

14.15. Траектории частиц. Пусть 2 - фшсшрованная контрольная точка и пусть Z + z - положение частицы воды в момент времени t; при этом предполагается, что модуль г' \ мал. Тогда для волн малой высоты скорость в точке z + г' будет отличаться от скорости в точке z членами второго порядка малости. Таким образом, из формулы (2) п. 14.13, если отбросим члены второго порядка, получим равенство

dz dt

uw acm . I ,4

Интегрируя это равенство и подставляя фиксированное значение 2, выбранное таким образом, чтобы произвольная постоянная интегрирования обращалась в нуль, и учитывая равенство с = п1т, получаем соотношение

. . COS (mz - nt).

Приравнивая действительные и мнимые части, находим равенства

, а cos (тх-nt) ch ту ~ shmA

, д sin (mjc-nt) sh my У ~ shfltA

следовательно.

1, a =

a ch my

sh mh

a ash my sh mh

Поэтому траектория частицы представляет собой эллипс с горизонтальной полуосью а и вертикальной полуосью Р и центр эллипса расположен в среднем положении частиц - в точке 2.

Средний уровень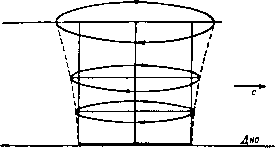

Рис. 264.

Так как а^ -aVshm, то все эллипсы имеют одинаковое расстояние между их фокусами, но длины осей эллипсов уменьшаются с погружением в глубину жидкости. На дне = О и, следовательно, Р = О, так что эллипс вырождается в прямую линию и частицы на дне просто движутся назад и вперед. Общий характер траекторий частиц, средние положения которых соответствуют одной и той же вертикальной линии, изображен на рис. 264.

Мы замечаем также, что фазовый угол (тх - nt) волны является одновременно эксцентрическим углом эллипса, так что каждая частица описывает свой эллипс за время, равное периоду волны, и все они находятся в одной и той же фазе. Вертикальная линия, Состоящая из частиц жидкости в начальный

момент, начинает изгибаться при движении жидкости, что иллюстрируется пунктирной линией на рис. 264; эта линия изгибается, подобно стеблю травы под действием ветра; однако жидкая линия, кроме того, и перемещается.

Следует заметить также, что все частицы, расположенные под гребнем или впадиной, движутся горизонтально на той же вертикальной линии. В частности, частица, находящаяся на гребне, движется вперед в наивысшую точку эллипса, в то время как во впадине она движется в обратном направлении в самую низшую точку эллипса. Это замечание относится к приливам и приливным течениям.

14.17. Прогрессивные волны на глубокой воде. Для волн, поверхностное возвышение которых определяется соотношением

Г] = а sin (mx - nt), (1)

комплексный потенциал задается формулой (2) п. 14.13 (рис. 265). Если перенести начало координат на невозмущенную поверхность, то получим

Рнс. 265.

комплексный потенциал в виде

ас cos (mz-\-mih - nt)

~ sh тЛ ~

= ас [cos (тг - nt) cth тЛ- г sin (тг - nt)].

1 и, следовательно, для волн

Если /г^ 00, то мы получим cth/п/г на глубокой воде

W = ace~ ~\

Скорость распространения волн на глубокой воде, согласно уравнению (3) п. 14.13, выражается формулой

т

так что скорость распространения пропорциональна квадратному корню из длины волны.

Для траекторий частиц, согласно результатам п. 14.15, имеют место уравнения

z - ае~ (mz-nt) Qg-i {mx-nt)gmy

Отсюда I г' = ае ч^, траектории частиц представляют собой окружности радиуса а. Когда - оо, то радиусы окружностей стремятся к нулю.

Для того чтобы в предыдущем исследовании воду можно было считать глубокой, необходимо только, чтобы выполнялось условие cth тЛ == 1 = th mh. Заметим теперь, что th 2,65 = 0,99; указанное условие выполняется в том