- <Ч^(-)(-)}-(- &)}+

+ /х In

-a*-2 a ...nV

Константу в этой формуле можно опустить, поэтому

Далее, функцию sinx можно разложить в бесконечное произведение по формуле

.п.,-,(1-5)(,-)...(,-

Если теперь устремить п к бесконечности, то мы получим комплексный потенциал бесконечной цепочки вихрей в форме

W = /х 1п sin

яг

Рассмотрим вихрь в точке г = 0. Комплексная скорость этого вихря равна --/-,xlnsin-i-/xlnz =-/X ctg-51-1 =0.

dz I a )г=0 \ a a z Jz=(i

Таким образом, вихрь, расположенный в начале координат, покоится. Следовательно, покоятся все вихри рассматриваемой цепочки. Это значит.

е-е-о-е-о-

-2а

2а

Рис. 256.

что сама цепочка вихрей не индуцирует скорости, которая могла бы привести в движение цепочку.

Функция тока получающегося течения дается формулой

2/ф = w{z) - w (г) = /х In ( sin - sin -

или

ф=1х1п1(сЬ

-cos

2лдг

При больших значениях отношения у1а мы можем пренебречь членом cos2nx/a, так как модуль его не превосходит единицы. Следовательно, вдоль линии тока ф = const мы можем считать у = const. Таким образом, на большом расстоянии от цепочки вихрей линии тока параллельны цепочке.

Кроме того, для комплексных скоростей Di и соответственно в точках гиг справедливо соотношение

2 sin--

1ХЛ . яг

--а-ctg -

. 2яу 2пх

ch -- - cos-

) См., например, Hob son. Plane Trigonometry, § 282. (На русском языке см., например. Лаврентьев At. А., Шабат Б. В., Методы теории функций комплексного переменного, Физматгиз, М., 1958.- Прим. перев.)

правая часть которого является чисто мнимой величиной и стремится к нулю прн у со. Таким образом, скорости на удаленных линиях тока по обе стороны от цепочки параллельны цепочке, но направлены в противоположные стороны. Таким образом, цепочка вихрей на больших расстояниях ведет себя подобно вихревому слою.

13.72. Вихревая дорожка Кармана. Вихревая дорожка Кармана состоит из двух параллельных вихревых цепочек, в которых расстояние между вихрями одинаково и равно а. Одна цепочка состоит из вихрей интенсивности х, а другая - из вихрей интенсивности -х. Вихри в верхней цепочке расположены над серединой отрезков, соединяющих соседние вихри в нижней цепочке

-а----ф-

- --О

.----------

Г а/2 а

Рис. 257.

(рис. 257). Рассмотрим эту конфигурацию при / = О и выберем систему координат, как показано на рисунке: ось д; расположим посредине между цепочками, отстоящими друг от друга на расстояние Ь, и направим ее параллельно цепочкам. Пусть в этот момент времени вихри верхней цепочки находятся в точках таАг Уг1Ь, а вихри нижней цепочки - в точках (т-)- Уг)а - Vtib, где т =

= 0± 1, ± 2----

Из предыдущего пункта следует, что при / = О комплексный потенциал этого течения имеет вид

. , . я / ib \ . , . я / а , ib Л

Так как ни одна цепочка не индуцирует скорости сама на себя, то скорость вихря в точке 2 = Via - Viib определяется формулой

1хл . / я . л6 л

Таким образом, нижняя вихревая цепочка перемещается вдоль оси х со скоростью

V = JifLth.

Аналогично можно показать, что и верхняя цепочка перемещается с такой же скоростью. За время T=a/V цепочки сместятся на расстояние а и конфигурация станет той же самой, что и в начале движения.

Чтобы исследовать устойчивость вихревой дорожки, заметим, что в некоторый момент времени / вихри верхней цепочки будут находиться

в точках ma + Vt ib, а вихри нижней цепочки -в точках (п + а-Ь -fVf - 2 ib, где тип пробегают весь ряд целых чисел от - со до +оо,

включая нуль. Если мы слегка сместим каждый вихрь, то вихри верхней цепочки расположатся в точках ma + Vt-\-т, а вихри нижней

цепочки -в точках (пa + Vt- ib + zn, где и zi, - бесконечно

малые величины. Дорожка будет устойчивой, если эти величины останутся малыми в течение всего времени движения. Теперь комплексная скорость вихря, который соответствует значению m = О, равна

Составляющие этой скорости от вихрей верхней цепочки, соответствующих ± т, и вихрей нижней цепочки, соответствующих - п-1и п, выражаются в виде суммы

Разлагая последнее выражение в ряд и сохраняя только члены первого порядка малости относительно г^, г^, г-т, zl . г\, мы получим

го -Zn

n+a+ib * (n+Ya-ib

- tx

(n+a-ib (n+a+ib

Если мы положим Zm=YCosm9, zi, = у'cos -f 9, где у и у' -

некоторые малые по модулю комплексные числа*), то последнее выражение можно будет привести к виду

2 vii-cos e) 2-(v-Vco<.+i)e)(( +l)-t.)

Далее, известно*), что имеют место равенства

□о

2ка хя , dzo

У J*.

о l+Ty +*

Таким образом, суммируя действие всех вихрей на вихрь, соответствующий значению т = 0, и принимая во внимание формулу (1), получим уравнение

) Это соответствует колебательному смешению цепочки. *) См. примечание на стр. 355.

где

tn=l

1-cos mQ

Чтобы получить уравнение для вихря из нижнего ряда, поменяем величину - X на X, а величину у на у', тогда получим

-2tx

(Лу + Су).

Для решения этих уравнений заменим в уравнении (3) все величины на комплексно-сопряженные, продифференцируем полученное уравнение по / и используем снова уравнения (3) и (4). Тогда мы получим уравнение относительно у

dti - а2 ( dt dt )- а*

Будем искать решение этого уравнения в виде

y = hexp(- ).

После подстановки этого выражения в уравнение получаем

Отсюда следует, что при > С* величина к будет принимать действительные значения и движение будет неустойчивым.

С другой стороны, если Л* < &, то величина к будет принимать чисто мнимые значения и движение будет периодическим, следовательно, устойчивым. Кроме того, при 9 = я мы получим С=0, т. е. каждый член ряда обращается в нуль.

Таким образом, прн 9 = я мы должны иметь равенство Л = О в качестве необходимого условия устойчивости по отношению к такого типа смещениям.

Чтобы найти величину Л, продифференцируем равенство (2) по k, тогда по.1учим

Кроме того, путем разложения функции в ряды Фурье, легко получить равенство

tn=l

1-со5е д^2я-9).

Отсюда при 9 = я получаем

л -}

4 2сЬ2Лл

Таким образом, Л = О, если сН*я = У^2, т. е.

А;я = 0,8814 или &= 0,281а.

Вихревая дорожка не будет устойчивой до тех пор, пока не будет выполнено это условие. Для более детального ознакомления с этим вопросом отсылаем читателя к книге Г. Ламба Гидродинамика ).

13.73. Сопротивление, вызываемое вихревым следом. В случае обтекания цилиндрического тела потоком при достаточно малых числах Рейиольдса (см. п. 19.62) обнаружено, что через определенный промежуток времени попеременно то с верхней, то с нижней кромки тела срываются вихри, и на

Q--------£) -----------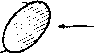

--( ----О--

Рис. 258.

некотором расстоянии за телом существует развитая вихревая дорожка*) (рис. 258). В непосредственной близости за телом форма вихревого следа неясна, на больших расстояниях от тела вниз по потоку вихри затухают вследствие вязкости, а в средней части существует описанная выше вихревая дорожка. Теперь мы получим приближенное выражение для сопротивления вследствие образования такого вихревого следа. Сделаем следующие предположения.

1) Вихри в следе могут быть представлены точечнымм вихрями.

2) В системе координат, начало которой выбрано посредине регулярной части следа, комплексный потенциал течения может быть приближенно заменен комплексным потенциалом бесконечной вихревой дорожки, выведенным в предыдущем пункте.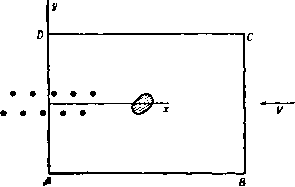

Рис. 259.

3) Если мы окружим цилиндр контуром, который перемещается с той же скоростью, что и вихревой след, и размеры которого велики по сравнению с размерами цилиндра, расстоянием между соседними вихрями в цепочке и расстоянием между цепочками, то движение жидкости на границах контура будет установившимся.

I) См. также Rosenhead L., Ргос. Roy. Soc. (А), 127 (1930), где исследуется устойчивость в случае, когда вихри имеют конечную площадь поперечного сечения. ) См. фото 11 - 12.

где

го = 4°+1<- (3)

В формуле (2) член Vz является комплексным потенциалом равномерного потока, наложенного на наше течение. Обозначим через - X - iV величину суммарной силы, действующей со стороны жидкости на цилиндр. Тогда на жидкость, заключенную в прямоугольнике ABCD, со стороны цилиндра действует сила X + iY и давление со стороны жидкости, окружающей прямоугольник.

Если обозначить через Я, 4- Ну количество движения жидкости, находящейся внутри контура ABCD, а через Р, -f iF обозначить количество движения жидкости, втекающей через контур ABCD, то по теореме Эйлера об изменении катнчества движения жидкости имеем

X-iY-i\ pdz -l{H,-iH,)+F,-iFy, (4)

(О

где через с обозначен контур прямоугольника ABCD.

Далее, нормальная скорость жидкости, втекающей через элемент ds контура, равна - дф/ds и, следовательно,

F.= -\Quds, F,= -\,vds.

(с) (с)

fx-= -jQ-d*. (5)

4) Образование вихрей в потоке происходит строго периодически.

Мы будем рассматривать цилиндр, который движется со скоростью U в покоящейся жидкости. Положим, что расстояние между вихрями в цепочке равно а, а расстояние между цепочками равно b (рис. 259). Тогда вихревая дорожка будет перемещаться со скоростью

V-th*-. (1)

где X- интенсивность каждого вихря. Так как вихри непрерывно срываются с тела через промежуток времени т, то период движения будет равен т и мы будем иметь V<U и {U - V)x = а.

Рас1Юложим ось х посредине между цепочками и направим ее в сторону движения. Если на наше течение наложить равномерный поток, скорость которого равна -V, то вихревая дорожка будет покоиться, цилиндр будет двигаться со скоростью U - V, а жидкость на бесконечности будет иметь скорость -V (исключая окрестность вихревого следа). Динамические условия при этом не изменяются.

Проведем теперь прямоугольный контур ABCD, размеры которого велики по сравнению с а, b н размерами цилиндра. Пусть сторона AD прямоугольника совпадает с осью у, выбранной так, чтобы начало координат было в центре параллелограмма, вершинами которого являются четыре ближайшие к началу координат вихря. Таким образом, на границе прямоугольника вихрей нет. Тогда комплексный потенциал течения будет иметь вид

Wi-Vz + ikln~~Vz+w, (2)

а

Поскольку течение на контуре ABCD установившееся, то из уравнения Бернулли следует

( о ( о

Интеграл от постоянной С равен нулю и. кроме того.

Таким образом.

(О (О (О

Подставив это выражение в формулу (4) и использовав формулу (5), мы по.1учим

(О

Далее, из формулы (2) следует, что

поэтому интеграл по контуру с от первого члена этого выражения обращается в нуль, а интеграл от второго ч.1ена является действительной величиной. Таким образом, величина сопротивления X является действительной частью функции

(О

и зависит от времени. Мы будем вычислять среднюю величину сопротивления.

Так как функция dwdz на контуре не зависит от времени вследствие предположения 3), а рассматриваемое движение периодическое с периодом т, то после интегрирования по / от О до т и выделения действительной части получаем следующую формулу для среднего по времени сопротивления D:

тО = { Л-( .).-/?.{if К (4 )dz}. (6)

В правой части формулы (6) первые два члена представляют собой увеличение количества движения жидкости вдоль оси х вследствие появления за время т внутри контура двух новых вихрей.

Спедовательно, для того чтобы найти первые члены в формуле (6). надо вычислить увеличение количества движения жидкости внутри большого контура ABCD вследствие появления в ней пары вихрей.

Рассмотрим выражение

Нх-Шу= J Q(u-iv)dS= -Q \ 4Т dS,

где wЫ\п(г~г ) - Ы\п(г - г„). Таким образом, если мы выберем для удобства вычиспений Zo=ih, -ih, то мы папучнм Н'х и Ну в виде

- co - оо

. -iCX 5 dy\\niz-ih)-\n(z : mlzlZ-

sin - f-

+ 2 ctg

a я(г + го)

Заметим, что dw/dz = О всюду на контуре, за исключением стороны DA. С1едовательно, интеграл берется в пределах z= iy= +ico и z= iy= -ico. Положим

in;.----- -TV--2 j-T-

, in(z-rZn) я / , 6 Л , (Я

Тогда

1).. Cj-f 1) Q.i ль j;o(Sf-i) 1 =-°°.

Подставляя это выражение в формулу (6) и используя формулу (7), мы получим формулу Кармана для сопротивления, которое обусловлено появлением вихревого следа

2лхд6 . 2nx-Q J лЬ яЬ \

~ т ~ а \ а а )

Сопротивление может быть выражено через скорость V в виде

при этом надо учесть, что a = x{U - V).

Следует подчеркнуть, что вычисления были проведены при некоторых предположениях, сформулированных выше, и результаты носят приближенный характер.

При изменении л; от - оо до +оо функция In (z -/Л) получает приращение - in или 1л в зависимости от того, у > h или у <h.

Таким образом, выражение в квадратных скобках под знаком интеграла равно 2л1 или О в зависимости от того, лежит ли величина у внутри отрезка -Л и Л или вне его. Следовательно,

И'х Шу = - фх dy (2л/) = 4лдх/1, П'х = 4лсхЛ.

-Л

Применяя этот результат к нашей задаче, мы найдем, что первые два члена в выражении (6) равны

2лдх6. (7)

Для вычисления интеграла в выражении (6) мы из формулы (2) находим

Следовательно,

Примеры

13.8. Вихрь в сжимаемом газе. Предположим, что линии тока течения являются окружностями и что на каждой такой окружности циркуляция равна 2лх.

Тогда если обозначить через q скорость на окружности радиуса г, то циркуляция 2nrq=2nx, откуда, используя обозначения п. 1.67 и формулу (7) п. 1.63. получим

x x

Очевидно, что величина г достигает минимума г„ при М-оо. Поэтому

н при увеличении г число М должно монотонно уменьшаться. Число Маха достигает критической величины М = 1 при

= = .1.10

Таким образом, если на окружности С (рис. 260) r=raiin. то внутри С ие может существовать движение жидкости, так что эта область должна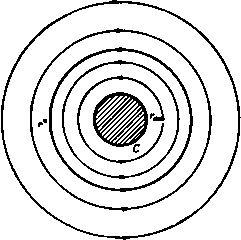

Р II с. 260.

быть свободной от жидкости или занятой центральным твердым ядром. В области между окружностью С и окружностью радиуса г* число М > 1 и течение является сверхзвуковым. При г > г* течение будет дозвуковым.

ПРИМЕРЫ К ГЛАВЕ 13

1. Пря\ о.1И11е|1ый вихрь движется в жидкости, ограниченной неподвижной п.ю-скостью. Считая движение жидкости плоскопара.1.1С.1ьиым, доказать, что линии тока не могут совпадать с линиями постоянного дап.1ения.

2. Доказать, что распре.теление давления от внхреисточпика такое же, как и распределение дав.1е1П1я от источника подходящей интенсивности.

3. Область П.10СК0СТИ х, у ограничена прямыми у=±с. В этой области существует плоское движение жидкости вследствие вихря, помещенного в начале координат. Доказать, что функция тока течения имеет вид

а 2ях -циркуляция вихря.

4. Исследовать движение дн\ х бесконечных параллельных прямолинейны.\ пихрей одинаковой интенсивности в безграничной жидкости.

Показать, что уравнение линий тока жидкости в системе координат, движущейся так, что координаты вихрей суть с, 0). имеет внд

\п\Цх~с) -~уЦ \{х^гУ-,-уЦ} - - --1= const.

5. Три параллельных прямолинейных вихря, интенсивность которых одинакова II имеет- одни и тот же знак, пересекают перпендикулярную им плоскость в точках, являющихся вершинами равностороннего треугольника со стороной а. Показать, что все эти вихри движутся по одной и той же цилиндрической поверхности с постоянной скоростью, и время одного оборота равно 2ла2/3х.

6. Бесконечная вихревая нить интенснвиост т находится около угла большого прямоугольного бака, заполненного идеальной жидкостью, и параллельна ребру бака.

Показать, что эта нить при движении вычерчивает в плоскости течения кривую

rsin20 = const и что это движение будет описываться уравнением гЩ = т/2.

7. Определить движение прямолинейной вихревой нити нитенсивностн х в бесконечной жидкости, ограниченной двумя перпендикулярными бесконечными плоскостями, линия пересечения которых параллельна этой нити. Показать, что вихрь перемещается из точки, равноудаленной от этих двух плоскостей, в любую другую точку за время, пропорциональное cfg20, где в - угол между одной из неподвижных плоскостей и плоскостью, проходящей через нить н линию пересечения неподвижных плоскостей.

Найти давления в точке Р на неподвижной плоскости в тот момент времени, когда плоскость, содержащая точку Р и вихревую нить, перпендикулярна неподвижной плоскости.

8. Два параллельных прямолинейных вихря интенсивности ki и fto движутся в идеальной безграничной жидкости и пересекают плоскость, перпендикулярную им. в точках Л и В. Пусть G - центр тяжести масс ft, и fto, находящихся в точках Л и S, а С - центр тяжести этих масс, если их поменять местами. Показать, что вихри движутся

вокруг точки G по окружностям с угловой скоростью, равной щг< скорость

частицы жидкости в точке Р этой плоскости равна /}р -

Доказать, что, когда треугольник АВР является равносторонним, частица жидкости в точке Р движется так, как если бы она была жестко связана с вихрями. Кроме того, доказать, что это утверждение справедливо, когда точка Р лежит на линии АВ и

где х = ОР/АВ, а точка О -середина отрезка АВ.

9. Вихрь интенсивности m находится внутри неподвижного цилиндра радиуса а, заполненного жидкостью, на расстоянии 6(6<о) от оси цилиндра. Считая движение жидкости безвихревым, найти движение вихря и сравнить его с движением вихря, находящегося в безграничной жидкости вне этого цилиндра (6>с), причем считать, что циркуляция вокруг цилиндра отсутствует.

В обоих случаях определить производную d<f/dt от потенциала скорости <f. 10. Тонкий прямолинейный вихрь находится внутри цилиндрического сосуда, образующая которого параллельна вихрю. Поперечное сечение сосуда ограничено полуокружностью радиуса а и диаметром, соединяющим концы полуокружности. Определить скорость вихря и доказать, что на радиусе, делящем полуокружность пополам, на расстоянии от центра, примерно равном 0,49 а, существует точка равновесия.

П. Прямолинейный вихрь интенсивности х расположен в безграничной жидкости вне неподвижного кругового цилиндра радиуса а. Вихрь параллелен оси цилиндра и находится от нее на расстоянии f. Циркуляция по любому контуру, не охватывающему вихря, равна нулю. Показать, что вихрь движется вокруг оси цилиндра с постоянной угловой скоростью, равной

Найти скорость жидкости в точке цилиндра, которая лежит в плоскости, проходящей через ось цилиндра и составляющей угол в с плоскостью, проведенной через ось

где