(II) Функция g обладает свойством симметрии g{z, z\ Z, Z) = g{Z, Z; z, I).

-g{Z, Z; Z, Z) = ((2, J; Z, Z)+g{Z, Z; z, i)), (6)

где индекс 1 означает, что после дифференцирования нужно положить г = Z, 2 = Z. Из свойства (II) следует равенство

(Jg{z, г, Z, Z))-4g(Z, Z; Z, Z). (7)

Этот результат является основным для настоящей задачи. Он получается непосредственно из свойства (II). В нашем случае из формулы (5) находим

g(Z, Z; Z, Z)=-ln(l--). (8)

Дифференцированием формул (5) и (8) легко показать, что эта функция удовлетворяет условию (7).

Теперь наложим на течение, индуцированное вихрем около цилиндра, некоторое другое течение, функция тока фо(2. 2) которого постоянна на границе цилиндра и не имеет особенности в точке z= Z (таким течением может быть, например, некоторый равномерный поток или циркуляция вокруг цилиндра). Функция тока полученного таким образом течения имеет вид

ф(г, )=фо(г, 2) + xG(z, г; ZZ). (9)

Чтобы определить комплексную скорость вихря, мы воспользуемся принципом, установленным в п. 13.22; для этого образуем функцию

Х = ф -xlnz -Z,

т. е. вычтем функцию тока вихря, действующего в безграничной жидкости. Тогда комплексная скорость вихря получится в виде (см. п. 13.22)

, , ,. 2/(),.

Далее, нз формул (5) и (9) следует равенство

Х = фо(г. 2)4 xg(2, г, Z,Z). (10)

Отсюда находим комплексную скорость вихря

2г-4Ч (И)

где

Xi=фo(Z, Z) + xg(Z, Z; Z, Z). (12)

Сравнивая формулы (10) и (12), мы видим, что множитель х в последнем члене выражения для х вследствие равенства (7) заменяется в последнем члене выражения для Xi множителем V x. Заметим также, что функция Xt = Xt (2 2) является функцией только величин Z,Z и не зависит от величины 2. Из формулы (11) мы получаем соотношения

функция Xi называется функцией тока Рауса.

В частности, если вихрь в точке (X, Y) является единственной особенностью течения и если фо (2, Z) зависит от времени посредством величин (X, К),

ТО вследствие соотношений (13) мы получим уравнение

dt дХ dt dY dt

Следовательно,

Xi(Z, Z)= const.

Это уравнение является уравнением траектории вихря (рис. 249).

В том случае, когда вихрь интенсивности х находится вне цилиндра, а на цилиндр наложена циркуляция х', функция тока фо = х' 1пг, где г = г|.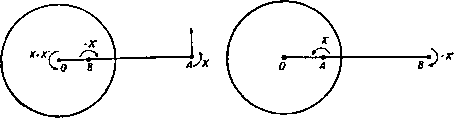

Рис. 249. Рис. 250.

Из формулы (8) следует, что g{Z, Z; Z,Z)= - 1п(1 -а ?*), где R=\Z\. Тогда траектория вихря определяется формулой

X, = X1п/?-1хIn (l-) = const, (14)

откуда следует, что радиус R остается постоянным и вихрь описывает окружность, концентрическую с цилиндром, со скоростью

Если вихрь находится внутри цилиндра, то функция, определенная формулой (8), оказывается непригодной, так как она имеет особенность в области течения в точке Z = 0. Однако и в этом случае комплексный потенциал можно получить из теоремы об окружности; он имеет вид

= /х' In г - /х In (-у- - Z) + /X In (г - Z).

Положим х4-х'=0, тогда мы получим течение, показанное на рис. 250, комплексный потенциал которого равен

ш = /х In (г - Z) - /х In (а* - zZ).

Мы теперь видим, что функция g, обладающая свойством симметрии, должна иметь вид

g(z, г, Z, Z)= --ln(a -zZ)(a -zZ). Отсюда следует равенство

g(Z, Z; ZZ)=-In(а -/?*). (15)

Таким образом, фо=0; траектория вихря задается уравнением Xi = - Y X In (а - R*) = const,

откуда следует, что вихрь снова описывает концентрическую окружность со скоростью xR/(a*-R*). Из наших рассуждений видно, что отражением

внутреннего внхря интенсивности х является вихрь интенсивности - ч, сопряженный с ним относительно окружности, и циркуляция вокруг цилиндра интенсивности - х.

В качестве последнего примера') рассмотрим вихрь интенсивности х, находящийся в точке Z вне цилиндра, который обтекается равномерным потоком, комплексный потенциал которого равен - i/ze- . На цилиндр наложена циркуляция интенсивности х'. Если обозначить через {R, в) полярные координаты вихря, то мы получим

%{Z, Z) = -fy (/?-)sin(e-a)+xln/?. (16)

Траектория вихря определяется формулой

Х,= i/(/? )sin(e-a) + xln/?-ln(l--) = const. (17)

Если на течение, индуцированное п вихрями интенсивности х, в точках г„ г= 1, 2, ..., п, наложить поток с функцией тока у\>о(г, г), то вследствие формулы (9) функция тока полученного течения примет вид

ф (г, г) = Фо (Z, z) + Z >irG (z, z; z z,), (18)

где суммирование производится по г от 1 до п. Составим выражения

Ф.= Фо(г.. z.)+S<rG(Zr, Zr] z z,), g = g(z z,; z z,), (19)

в которых суммирование проводится по s от 1 до п.

Тогда из формулы (И) следует, что комплексная скорость вихря в точке Z, равна v где

Таким образом, функция (20) вполне аналогична функции ¥ из п. 13.24 и остается постоянной во все время движения, если фо не зависит явно от времени. Функция g была найдена для внешности круга в виде (5) и для внутренности круга в виде (15). Если же граница области движения не является окружностью, то конформным отображением области движения на внутренность или внешность круга эту задачу можно свести к одной нз рассмотренных здесь задач. Выражение для функции g в новых переменных, полученных нз старых конформным отображением, получается с помощью формул (4) и (5) п. 13.60.

13.51. Вихри около кругового цилиндра. Рассмотрим вихрь х в точке А с координатой Zi и вихрь -X в точке В с координа- Рис. 251.

той 7 которые расположены вне

кругового цилиндра \z\ = a (рис. 251). Если 61 цилиндра не было, то комплексный потенциал течения имел бы вид ix In (г -Zi)/(z -Zj). Если же в области течения имеется круговой цилиндр г|=а, то из теоремы об

*) Для детального изучения кратко описанного здесь метода отсылаем читателя к статье: L i п С. С, On the motion of vortices in two-dimensions, Univ. Toronto Press, 1943. В этой статье задача решается в наиболее общей постановке.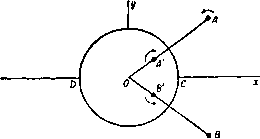

окружности получим комплексный потенциал

Отсюда следует, что отраженная система состоит из вихрей противоположных знаков, расположенных в точках, сопряженных относительно окружности с точками Л и В. Можно записать а = jx In (г -г,)-hcfz, где с точностью до постоянной

Шг = - ix In

Комплексная скорость вихря в точке Л равна -dw/dz при 2 = г,. Если записать, как в п. 13.50,

w = (f+iycG = (p+ix (g4-lnz -2i),

так что

+ 1п

g{z, Z; 2 2i)= -lnZ-2i -In

то траектория вихря в точке Л может быть получена в виде

- 2,

const= (i, Zb Zi, zi) = l-xln

ABAA

Отсюда следует равенство

AB-AA2kAB,

где й -некоторая постоянная, зависящая от начальных условий.

Если (х, у) или (г, 0) - координаты точки Л, то имеет место соотношение

,sin0(r-)=fe[r+-2a*cos20]\

которое в декартовых координатах имеет вид

(дс + у^- а ) у = 1(х^ -Ь у - af + 4aYl

Если положить = О, то получим уравнение цилиндра и оси х, т. е. разветвляющуюся линию тока.

Саедовательно, теперь мы можем нарисовать вид траекторий (рис. 252). Траектории состоят из двух петель внутри цилиндра и кривых вне цилиндра, имеющих асимптотами прямые у= ±k, так как при х->со, y-k*.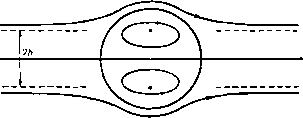

Рис. 252.

Внешние кривые описываются парой вихрей, расстояние между которыми на бесконечности равно 2Ь, где b есть значение постоянной к. Внутренние петли описываются парой вихрей внутри цилиндра. Движения внутри и вне

цилиндра могут существовать вместе, но линия, соединяющая соответствующие вихри внутри и вне цилиндра, не может проходить через центр круга.

Петли траектории могут вырождаться в точки. В этом случае внутри цилиндра будет находиться пара неподвижных вихрей. Чтобы получить условие этого вырождения, поместим все четыре вихря на оси у и обозначим расстояние точки А' от центра через г. Точка А' будет неподвижной в том случае, если индуцированная в ней скорость будет равна нулю, т. е. если

I , L 1 о

---flV-

Отсюда получаем уравнение г* + 4aV* - а* = О, которое дает

.-=1/5 -2 = 0,236067, =0,486.

В этом случае пара вихрей, расположенная внутри цилиндра, будет оставаться неподвижной.

13.52. Стационарные вихревые нити около цилиндра. Если в течении, изображенном на рис. 251, мы поменяем направление вращения всех вихрей, то движение вихря А будет задаваться формулой (1) последнего пункта, в которой всюду изменен знак перед величиной х.

Наложим на это течение равномерный поток, скорость которого на бесконечности равна и и направлена вдоль оси ОХ. Комплексный потенциал обтекания цилиндра равномерным потоком имеет вид

Следовательно, движение вихря А определяется функцией

Отсюда видно, что вихрь А будет находиться в покое, если dwjdz - 0 при z = Zi. Выполняя дифференцирование и опуская для простоты индекс 1, мы получаем соотношение

и Г1 --1) =Ы (-)(-°)i:gMfz=il . (2)

V У (zr-a2)(z-z)(22-a2)

Если два комплексных числа равны, то равны и сопряженные им числа. Выпишем сопряженное соотношение для соотношения (2) и разделим одно на другое, тогда получим равенство

(г* -а ) Z* (г=- а*) (гг-аг) + а2 (г-z) (i -a2) 22~ a2)(zz -a )-fa2(2 -2)

Это равенство легко привести к виду

(zz-a) + zz{z-zf=0. (3)

Отсюда, полагая г=гев, где 0<6 < я/2, получаем

(г - = 4г* sin 9, или (г ) . 2г sin 0.

Следовательно, ЛЛ=ЛВ;если это условие выполняется, то вихри позади цилиндра могут находиться в покое.

Из формул (2) и (3) получаем для этого случая

х= и

(г^-а^Т- (га + а )

Из соображений симметрии ясно, что если вихрь А неподвижен, то вихрь В тоже будет неподвижен. Таким образом, оказывается, что вихри, интенсивность которых отличается знаком, а величина интенсивности определена полученной выше формулой, могут покоиться позади кругового цилиндра, помещенного в равномерный поток, скорость которого U, причем вихри находятся в точках, являющихся отражением точек А н В, и, кроме того, АА-АВ.

Этот результат очень интересен, так как такие вихри часто наблюдаются при обтекании цилиндра потоком с малой скоростью (см. фото 1-6).

Р и с. 253.

Общий вид линий тока рассматриваемого течения показан на рис. 253. Из этого рисунка видно, что в области течения существует пять критических точек. Четыре из них находятся на цилиндре и одна находится на оси потока.

Комплексный потенциал течения жидкости получается из формулы (1) добавлением члена - 1х1п(г -2,), который является комплексным потенциалом вихря А.

13.60. Конформное отображение. Пусть в точке П плоскости С существует вихрь и пусть точка Р в плоскости z соответствует точке П при конформном отображении

гЧИ)- (1)

Обозначим через у некоторую замкнутую кривую, содержащую малую окрестность точки П, а через с -некоторую кривую, являющуюся отображением кривой Y и, следовательно, охватывающую точку Р (рис. 254). Если функция

tt = ф 4- Ф (2)

является комплексным потенциалом некоторого безвихревого течения жидкости в плоскости то будет существовать соответствующее ему безвихревое течение в плоскости г, которое получится исключением С из формул (1) и (2). При этом величины ф, ф и в соответствующих точках будут равны. Следовательно, будут равны и циркуляции вдоль кривых у и с, т. е.

(V) (с)

Таким образом, если в точке П существует вихревая нить интенсивности X, то в соответствующей ей точке Р также будет существовать

вихревая нить интенсивности хОднако ниоткуда не следует, что при движении эти нити будут оставаться в точках, соответствующих друг другу при конформном отображении. Тем не менее если мы знаем движение одной вихревой нити, то можем определить движение другой с помощью теоремы Рауса. Эту теорему можно получить следующим образом.

г-плоскость

Рнс. 254.

Обозначим через С, координату точки П, а через г, координату точки Р (рис. 254). Предположим, что преобразование (1) конформно отображает внешность профиля А в плоскости г на внешность цилиндра С или круга \1\ = а в плоскости (см. рис. 109).

Метод конформного отображения позволяет нам установить соответствие между течениями в этих двух плоскостях с помощью их функций тока, например:

ф(г, 2) = (о(С. Q- (3)

Если одна из этих функций задается, то другая определяется из последнего равенства.

Если единственной особенностью в области течения в плоскости z является вихрь интенсивноси х в точке Zj и, следовательно, вихрь интенсивности x в точке то траектория вихря в плоскости ? задается функцией Хи определяемой формулой (12) п. 13.50. Эта формула с очевидным изменением обозначений имеет вид

Xi = Wo(Si. Ti) 4--xy(Ci. Ci. Si), где функция y задается формулой (5) п. 13. 50 в виде

y(C. Ь Ci. С.) = г(С. С; С ri)-inC-Sil-

Тогда в плоскости z мы имеем

g{z, z\ Zi, zi) = G{z,z; г„ z,)-ln2-Zi.

где G-неизвестная функция, имеющая особенность в области течения только в точке г=г, и обладающая свойством симметрии [см. формулу (4) п. 13.50]. С другой стороны, функции Г и G являются функциями тока, одна переходит в другую при конформном преобразовании (1). Следовательно, функции Г и G принимают одни и те же значения в соответствующих точках. Таким образом, вычитая из функции g функцию у, получаем

g{z, г; Zi, 2,) = У (С, I; С. In

Спедовательно, устремляя z к 2 получаем равенство

giZi, Zi, Zi, 2,) = y(Ci. Сг. Ci. ?i) + ln

) Cp. П. 8.50. Предполагается, что одному обходу кривой у соответствует один обход кривой с.

= ixln(Z-Zo) - х1п (--Z ) ,

которая вместе с формулой (1) определяет w как функцию z. Таким спосо бом может быть исследовано любое распределение вихрей (см. пп. 8.70, 8.71).

13.62. Эквивалентный слой Грина из источников и вихрей. Будем испо.1ьзовать обозначения п. 8.24. Так как комплексная скорость ы -<Ъ = ~d-jDldz является аналитической функцией переменной z в области течения L, ограниченной контуром С, то по формуле Коши (п. 5.59) получим следующие равенства:

4й Sru-iv или О, (I)

Это равенство определяет функцию g через известную функцию у; следовательно, траектория вихря в плоскости z задается равенством Х=const, где

x=x. + xinf;-

Это и есть утверждение теоремы Рауса.

В качестве иллюстрации теоремы найдем траекторию вихря интенсивности X, движущегося в плоскости г около плоской пластины ( - 2а, 2а). Такая пластина отображаемся на окружность СI = а преобразованием Жуковского

z=C + f .

Но соответствующая задача для круга уже решена [см. формулу (14) п. 13.50]. и мы воспользуемся этим решением. Для простоты (положим х' = 0, так что если г (cos 9 4-sin 9), то

Х,= --J-xln(l- -J) , -l-=i °J (cos2e-Jsin29).

Таким образом, в плоскости z получим

X.--b<-)- ln(l-cos29 + i),

1 = ( + ) cos 9, t/, = (г - sin е.

Траектория вихря определяется равенством х = const. На это течение можно наложить равномерный поток и циркуляцию вокруг пластины [см. формулу (16) п. 13. 50). Решение такой задачи не представляет дополнительных трудностей.

13.61. Вихрь вне произвольного цилиндра. Как и в случае источника, описанного в п. 8.71, комплексный потенциал искомого течения может быть выписан с помощью отображающей функции

2 = /(Z).

которая переводит внешность контура С цилиндра в плоскости z во внешность единичной окружности Z=1 в плоскости Z. Таким образом, если в точке Zo вне контура С существует вихрь интенсивности х, то в соответствующей ей точке Zq вне единичной окружности в плоскости Z существует вихрь интенсивности х. В силу теоремы об окружности комплексный потенциал выражается формулой

в зависимости от того, где находится точка z -внутри контура L или вне его. Здесь через (u - iv)c мы обозначаем значение комплексной скорости u - iv в точках контура С. Пусть 9, -тангенциальная составляющая скорости на контуре, направленна^ в сторону положительного обхода контура С, <7 - нормальная составляющая скорости, направленная внутрь области L. Тогда

{и - iv)c = (U - iv)c dse = {q, - iqn) ds, (2)

следовательно, в точке z области течения по формуле (1) получим равенство

(С) (С)

Это равенство является комплексной скоростью в точке г, обусловленной источниками и вихрями, распределенными на контуре С с плотностью соответственно qJ2n и q,/2n на единицу длины. Формула (1) показывает, что эта система не индуцирует поля скоростей вне области L.

13.70. Вихревая пелена. В п. 13.20 мы определили прямолинейный вихрь как предельный случай цилиндрической вихревой трубкн, когда поперечное сечение ее стягивается в точку, а поток внхря остается постоянным. Теперь мы используем аналогичный прием, чтобы определить вихревую пелену.

На рис. 255 через п обозначен вектор единичной нормали в точке Р поверхности 2. Пусть е - положительная бесконечно малая скалярная величина; рассмотрим точки Ро и Pi, радиусы-векторы которых проведены из точки Р и равны V en и -V2 en.

Когда точка Р описывает поверхность 2, точки Ро и Pi описывают поверхности So и S эквидистантные поверхности 2. Рассмотрим элемент поверхности 2, площадь которого равна ds, а центр тяжести находится в точке Р. Нормали к поверхности 2 на границе элемента ds и касательная плоскости к поверхностям Sg и S, ограничивают малый цилиндр, объем которого равен dT = е dS.

Представим себе, что наши поверхности находятся в движущейся жидкости, завихренность которой всюду равна нулю, за исключением области, расположенной между поверхностями S, и S. Обозначим через g BiKTop вихря в точке Р. Тогда мы можем записать Jdx = EdS = uidS, где

<o = ge. (1)

Если теперь устремить величину е к нулю, а величину завихренности 5 к бесконечности так, чтобы вектор ю оставался постоянным, то мы получим поверхность 2, называемую вихревой пеленой, интенсивность которой на единицу площади равна w.

Прежде чем переходить к пределу, заметим, что скорость жидкости всюду непрерывна и имеют место равенства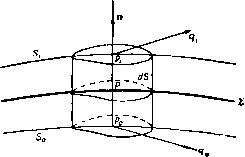

Рис. 255.

qi=q+ 2 e(nV)q, q. = q -у е (nV) q,

где через q, q, и Qo обозначена скорость в точках Р, Р, и Ро- Складывая эти два равенства, получаем

q = Y(q + qi). (3)

Этот результат верен при малых значениях величины е. Таким образом, скорость в точке Р вихревой пелены является средним арифметическим скоростей в точках, близких к точке Р и лежащих на нормали к поверхности 2 по разные стороны от поверхности.

Если мы применим теорему Гаусса [см. формулу (2) п. 2.61 ] к элементарному цилиндру объема di (рис. 255), положив а = q, то получим приближенное равенство

d5 = п X (qi - qo) dS.

При этом мы опустили члены более высокого порядка малости, получающиеся за счет искривленной части поверхности цилиндра. Если последнее равенство разделить на dS и устремить е к нулю, то с помощью формулы (1) получим точное равенство

© = nx(qi-qo) (4)

для поверхностной интенсивности вихревой пелены ю.

Ясно, что отличное от нуля значение вектора ю связано с разрывом компонент скоростей qo и q перпендикулярных вектору п. Следовательно, поверхность, на которой тангенциальная составляющая скорости терпит разрыв, является вихревой пеленой.

Из формулы (4) видно также, что вектор ю перпендикулярен вектору п и, следовательно, направлен по касательной к вихревой пелене. Двумерная вихревая пелена представляется в плоскости течения линией АВ, на которой тангенциальная составляющаяскоростн терпит разрыв. Нормальная составляющая скорости при этом разрыва не терпит.

Например, при гребле лопасть погруженного весла разделяет жидкость, движущуюся в противоположных направлениях вдоль поверхности весла (ср. рис. 114). Когда гребец быстро вынимает лопасть из воды, в жидкости образуется тонкая пленка, в которой касательная составляющая скорости резко изменяется; эту пленку можно считать вихревой пеленой. Эта пелена неустойчива и свертывается в вихрь, который обычно и наблюдается. Подобное объяснение можно предложить и для вихрей, которые образуются за краем ложки в чашке с чаем.

Важно заметить, что образование вихревой пелены, например, в следе движущегося крылового профиля не противоречит теореме об отсутствии вихрей в жидкости, которая начала двигаться из состояния покоя под действием приложенного импульса.

В некоторых случаях (см. фото 11, 12) вихревой след за телом состоит из двух цепочек вихрей. Его можно рассматривать как части вихревой пелены, свернувшиеся в сосредоточенные вихри. В связи с этим мы должны будем развить теорию двух цепочек вихрей.

13.71. Одна бесконечная цепочка вихрей. Рассмотрим бесконечную цепочку вихрей, интенсивность каждого из которых равна х, расположенных в точках

О, ±а, ±2а, ..., ± па.....

Комплексный потенциал 2п -\- 1 вихрей, расположенных по обе стороны от начала координат (рис. 256), имеет вид:

Wn = /х Inz-f /х ln(z -а) -- ... 4-/Х 1п (г -па) + + iyc\n(z + a)-\-... + ix In {z + па) = = /X In [z (г* - a*) (z* - 2*a )... (z - n*a*)} =