где П - давление на бесконечности. Используя формулу (1), найдем, что

xe ..... гт > *е

или Ро = П

График зависимости давления от радиуса показан на рис. 239, где через у обозначено отношение давления р в данной точке и давления П на бесконечности, через X обозначено отношение г/а, k = х*д/а*П. Кривые являются параболами

1/ (1 /г) = /гд* и {y-\)x* = -\k.

Последняя парабола имеет асимптотой прямую у = \. Кривые касаются в точке JC = 1, которая соответствует границе вихря. Штриховыми линиями нарисованы продолжения этих кривых. Можно видеть, что давление непрерывно возрастает, начиная от величины П (1 - k), и стремится к П на бгёконечности.

Рис. 239.

13.12. Кольцевой круговой вихрь. Мы только что видели, что давление в центре вихря минимально и имеет величину П (1 - k). При k > 1 давление было бы отрицательным, однако это физически не выполнимо. Поэтому внутри вихря будет образовываться концентрическая область, не содержащая жидкости. Диаграмма давления, приведенная на рис. 239, теперь должна быть изменена путем переноса начала координат в соответствующую точку между точками у=\ - kHy=\ - Vi/t. В качестве крайнего случая мы можем положить /г = 2, т. е. х*е = 2а*П. Тогда мы получим незаполненную жидкостью цилиндрическую область, вокруг которой существует циклическое безвихревое движение.

Кроме того, оказывается, что если задана циркуляция 2ях и давление на бесконечности II, то круговой вихрь, внутренность которого полностью заполнена жидкостью, имеет минимальный радиус. Величина этого радиуса определяется по формуле а' = (ср. п. 13.80).

13.13. Комбинированный вихрь Рэнкина. Комбинированным вихрем называется вертикальный цилиндрический вихрь, существующий в жидкости, движущейся под действием силы тяжести. Давление П на верхней поверхности жидкости равно атмосферному. Эта задача является трехмерной, но ее удобно рассмотреть здесь.

Выберем начало координат в точке пересечения оси вихря с плоскостью уровня жидкости на бесконечности (рис. 240). Ось г направим вертикально-

вниз. Очевидно, что кинематические условия на границе жидкости удовлетворяются системой скоростей, найденной в п. 13.10, а именно (мы будем писать

2(0 вместо со) мы можем принять q = cor, если г < а, и 9 = соу, если г > а.

Рис. 240.

И в том и в другом случае векторы скорости жидкости горизонтальны и перпендикулярны радиусу г. При г > а движение безвихревое, так как имеется потенциал скорости ф = -а^соЭ. Следовательно, уравнение для давления имеет вид

7+ 2 -г --яг = const,

где -г -потенциал гравитационного поля. Чтобы определить константу, положим г=со, 2 = 0. Тогда получим р = П, где П -давление на поверхности жидкости на бесконечности, следовательно,

Для определения давления р, внутри вихря мы имеем уравнения движения

Q дг Q дг

Таким образом.

Чтобы определить постоянную С, мы должны положить p = Pi при г = а. Тогда мы получим

Pi = П + gQZ-aw*Q( 1 -з^-) .

На свободной поверхности р = р, = П, следовательно, из формул (1) и (2) находим

г = s-, если г > а

если г < а.

Эти формулы определяют форму свободной поверхности.

Кроме того, оказывается, что поверхности постоянного давления получаются путем переноса по вертикали свободной поверхности, которая соответствует значению

/? = /?, = П.

Чтобы получить глубину впадины в точке А относительно уровня жидкости на бесконечности, положим в формуле (3) г = 0. Тогда мы получим

0Л = .

13.20. Прямолинейная вихревая нить. Интенсивность кругового вихря была определена в п. 13.10 формулой

2

где ла* - площадь поперечного сечения вихря. Если мы устремим величину а к нулю, а величину ш к бесконечности так, чтобы интенсивность оставалась постоянной, то мы получим прямолинейную вихревую нить, т. е. двумерный вихрь, поперечное сеченне которого является бесконечно малым кругом (ср. п. 1.12).

В п. 13.12 установлено, что при заданных значениях циркуляции и дав-.пении на бесконечности вихрь имеет некоторый минимальный радиус, поэтому введенная нами вихревая нить должна рассматриваться лишь как удобная абстракция (ср. п. 8.10).

Прямолинейная вихревая нить представляется точкой в плоскости движения, точно так же, как двумерный источник. Из п. 13.10 следует, что комплексный потенциал течения, индуцированного вихревой нитью интенсивности X, расположенной в точке 2о. задается формулой

W = /Х In (Z - 2о)-

Интенсивность х положительна, если циркуляция вокруг нити направлена против часовой стре.чкн. Мы можем называть такую нить точечным вихрем или просто вихрем, если это не повлечет за собой неясностей.

13.21. Изолированная вихревая нить. Пусть через точку А с координатой Zo проходит вихревая нить интенсивности х (рис. 241). Тогда w = = /х1п(г -го), следовательно, скорость в точке Р с координатой г находится по формуле

dw Ы -ix

V - и - IV =---.

где R-AP, а arg(? -го)=0. Отсюда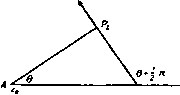

Рнс. 241.

Таким образом, направление движения в точке Р перпендикулярно отрезку ЛР, а скорость q=xiR имеет направление вращения жидкости, созданного вихрем в точке А.

Следует заметить, что функция тока выражается формулой

\) у X In (г - Zo) (г - Zo) = X In I г - 2о I = 1 п /?.

Кроме того, так как 2/ij5= - ш(г), мы получим соотношение

13.22. Движение вихревых нитей. Мы уже видели (п. 13.10), что изолированный круговой вихрь не может перемещаться в жидкости, то же самое, следовательно, справедливо и в случае вихревой нити. Таким образом, если существует несколько вихревых нитей, то движение нити, расположенной в точке Р, совпадает с движением, которое создавали бы в точке Р остальные вихри, если бы вихрь в точке Р отсутствовал. Однако следует заметить, что общее движение жидкости может существовать не только вследствие наличия вихрей, но также вследствие наличия источников, потоков или других причин. Тогда скорость в точке Р будет равна сумме скорости, индуцированной другими вихрями, как только что было описано, и общей скорости жидкости в точке Р вследствие всех причин.

Пусть через w обозначен комплексный потенциал течения, содержащего несколько вихревых нитей. Тогда комплексная скорость вихря интенсивности X в точке Zo равна

о

-iVo= -{-j-[ay-jxln (z-2o)]]-= -2/{-[if-xlnz -Zol J

где индекс О указывает, что после дифференцирования мы полагаем z= Zq, а z = 2o.

13.23. Две вихревые нити. Рассмотрим вихревые нити интенсивности X, и Xj, представленные в плоскости движения точками /4, и /4, (рис. 242). Если обозначить координаты точек Л, и At через z, и Zt, то комплексный

потенциал запишется в виде

Ш= JX, In (Z - Zj) + Хг In (z - Zi).

Скорость, индуцированная вихрем х., в точке .4 равна

ы, -1:>, = - . (1)

Z\ - -2

Аналогично скорость в точке равна

Рис. 242.

X, ( , - iVx) -f Xj ( 2 - ivt) = 0.

Если поместить в точки /4, и At материальные точки, массы которых равны X, и Xj, то координата центра тяжести G этих точек будет равна (x,z,-(-X2Z2)/(x,-f-Хг) при условии, что Xj + Хг =ifc 0. Мы назовем точку С центром тяжести вихрей. Из формулы (3) следует, что центр тяжести вихрей остается неподвижным.

Скорость в точке Л, равна

х, + хг А,А\

где

Следовательно, прямая /4И вращается с угловой скоростью со. Так как ни один вихрь не индуцирует скорости, направленной вдоль прямой AiA, то длина отрезка AiA остается постоянной. Отсюда следует, что угловая скорость со постоянна и каждый вихрь описывает с постоянной скоростью некоторую окружность.

Если X, = Х2 = х, Л,/4г = о, то каждый вихрь описывает с угловой скоростью 2х/а* окружность, диаметром которой является отрезок AiA.

13.24. Движение системы вихревых нитей. Если мы рассмотрим систему вихревых нитей интенсивности х щ, Хз.....помещенных в точки

Zi, Zi, Zs, то из предыдущего пункта сразу увидим, что функция

W = J2XrX, ln(Zr-2,), Гф5,

дает скорость, индуцированную в точке любого вихря всеми остальными вихрями.

Если для простоты рассмотреть три нити, то можно записать W = i {xiXj In (z, - Zj) -f XjXs In (Z2 - Zi) + ЯзЩ In (гз- z,)}. Скорость, индуцированная на первой нити, равна

1 dW

I zi -г, г, -гз J

Выписав соответствующие скорости вихревых нитей интенсивности х, и Хз, после элементарных операций умножения и сложения мы получим формулы

Х,Ы,Ч-X2U2-fX3U3=0, Х,0,-f Х2У2 + ХзУз = 0. (1)

откуда следует, что центр тяжести трех вихревых нитей остается в покое. Легко видеть, что этот результат можно обобщить на любое число нитей. Если мы запишем функцию W в виде

W=Ф + iW,

то получим

X, (Ы, - IVi) =--x- = -т--/ .

dzi dXi dXi

Отсюда непосредственно следуют формулы

.дф dW dW

Следовательно, компоненты скорости самого вихря получаются из функции W таким же путем, как компоненты скорости течения получаются из функции тока. Кроме того,

V f dxr . dV dyr

dV yr, f dW dxr dt Zl\ dXr dt

dyr dt

- ir - --

dx,

dt ~ X, dy, dt Kr dx.

Следовательно, = 0 и функция W остается постоянной во все время движения.

13.30. Пара вихрей. Два вихря, интенсивности которых одинаковы по величине, но противоположны по знаку, называются парой вихрей. Рассмотрим такую пару: вихрь интенсивности х помещен в точку А, вихрь интенсивности - х помещен в точку В, причем /4S= 2а. Расположим ось х посредине между точками А н В к направим ее перпендикулярно отрезку АВ

(рис. 243). Вихрь в точке А индуцирует в точке В скорость, параллельную оси х и равную х/(2а); вихрь в точке В индуцирует в точке Л такую же скорость. Отсюда следует, что пара вихрей движется в направлении оси Ох с постоянной скоростью, равной х/(2а). Комплексный потенциал течения имеет вид х/(2а)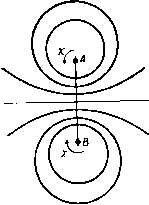

а = ix In

г - ai z-\-ai

если начало координат О выбрано в середине отрезка АВ.

Следовательно, функция тока имеет вид

Рис. 243.

где через Р обозначена произвольная точка. Таким образом, мгновенное положение линий тока задается равенством Pi4/PS = const; линии тока являются окружностями, имеющими точки Л и Б предельными точками, а ось основной осью).

Скорость в любой точке на оси Ох направлена вдоль этой оси, и, следовательно, через эту линию нет расхода жидкости. Скорость в точке О равна 2х/о, т. е. в четыре раза больше скорости движения пары вихрей.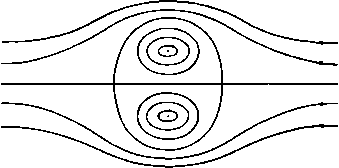

Рис. 244.

Чтобы найти линии тока движения жидкости относительно пары вихрей, надо на все течение наложить скорость, равную скорости движения вихрей, но направленную в противоположную сторону. Тогда можно показать, что функция тока должна иметь вид

где r = РА, г2РВ. Вид линий тока в относительном движении показан на рис. 244.

) в биполярных координатах (п. 6.50) комплексный потенциал пары вихрей имеет вид W--xZ. при условии, что координаты точек А ч В суть г=±с. Связь между задачей, рассмотренной в п. 6.53, и излагаемой здесь теорией теперь становится очевидной.

Полуоси овала приближенно равны 2,09а и 1,73а (Кельвин).

Кроме того, течение, показанное на рис. 244, может быть интерпретировано, как обтекание цилиндра, поперечным сечением которого является данный овал.

Если обозначить скорость потока на бесконечности через U, то мы имеем и = х/2а, и, следовательно, мы можем считать это движение обтеканием вихрей А н В интенсивности ± 2aU потоком, скорость которого на бесконечности равна U.

13.31. Вихревая нить, параллельная плоскости. Пусть в точке А, отстоящей от плоскости ОХ на расстоянии а, помещена вихревая нить, АО=а (рис. 245). Интенсивность вихревой нити равна х. Если мы продолжим область течения через плоскость ОХ и поместим в точке В, расположенной на расстоянии 2а от точки А, вторую вихревую нить интенсивности - х, то получим пару вихрей, которая не создает потока жидкости через плоскость ОХ. Саму плоскость тогда можно убрать. Таким образом, вихрь В является зеркальным отражением вихря А относительно плоскости ОХ. Так как пара вихрей движется параллельно осн ОХ со скоростью х/(2а), то, следовательно, один вихрь А в присутствии плоскости будет двигаться параллельно этой плоскости с той же скоростью. Если вихри расположены так, как показано на рис. 245, то комплексный потенциал течения имеет вид

Ш= iX In -i-..

z + ai

Отсюда видно, что в момент времени / комплексным потенциалом является функция

. , z - ai - Vt

W= 1у(.\П -i--ггг ,

z~\-ai - Vt

где V = x/(2a).

Из этого соотношения находим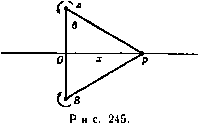

dt ~ \z-ai-Vt z+ai-VtJ

следовательно, в произвольной точке плоскости ОХ в момент времени/ = 0 имеем соотношение

/аф\ 2оУх х*со5 9

\ dt Jt=o xi~{-ai~ а*

Кроме того, при /=0 скорость точки Р на оси Ох равна сумме скоростей х/РА и х/РВ, перпендикулярных отрезкам РА и РВ, т. е. равна =2xcos9/a. Таким образом, давление в точке Р дается формулой

р 2х* cos* 9 cos* 9 П е а* а Q

где И -давление на бесконечности (при 0=я/2). Отсюда

p=II .cos e.cos 29.

Сила, действующая на плоскость вследствие движения вихря, равна

COS*9COS 26.sec*8de=0.

-я/2

13.32. Вихревой диполь. Рассмотрим пару вихрей: один интенсивности х в точке ас , другой интенсивности - х в точке -ае- (рис. 246). Если мы устремим величину а к нулю, а величину х к бесконечности так, чтобы 2ах = ц, мы получим вихревой диполь, ось которого наклонена под углом а к оси X (ср. п. 8.23).

Направление диполя считается от вихря с отрицательной интенсивностью к вихрю с положительной интенсивностью. Комплексный потенциал этого течения имеет вид

ш = lim ix [In (z - ae ) - In (z + ae )] =

a->e

= 1L4- ----2zS---J=--

Функция тока течения равна ф= - ficos(а -8)/л Если, в частности, мы возьмем диполь в начале координат и ось диполя направим вдоль оси у, то получим ф= - nsin9/r. Если мы положим ц= Ub*,

то получим выражение

(/62 sine =--7-

которое является функцией тока для кругового цилиндра радиуса Ь, движущегося со скоростью и вдоль оси X.

Таким образом, движение жидкости, вызванное круговым цилиндром. Рис. 246. совпадает с течением, индуцированным

вихревым диполем данной интенсивности, помещенным в центр цилиндра, причем ось диполя перпендикулярна направлению движения.

Циркуляцию вокруг цилиндра мы получим в том случае, если в центр цилиндра поместим вихревую нить нужной интенсивности.

13.33. Вихреисточник. Результаты предыдущего пункта приводят нас к вопросу, как комбинировать источник и вихрь. Комплексный потенциал

w= ( - m + ix)\nz

уменьшается на величину 2я(/т4-х) при одном обходе вокруг начала координат. Следовательно, потенциал скорости ф уменьшается на величину 2ях, а функция тока ф уменьшается на величину 2ят при одном обходе вокруг начала координат. Таким образом, функция w удовлетворяет условиям для вихря и источника.

Функция тока этого течения имеет вид

ф= -тб 4-х In г.

Если функция ф имеет постоянную величину xlnC, то мы отсюда получаем соотношение

из которого следует, что линии тока являются логарифмическими спиралями.

Линии тока могут быть легко нарисованы с помощью диагонального метода (см. п. 4.32) путем наложения линий

т9 = лш,

X 1пл = лш, л = О, 1, 2, ...

или

9=- со. т

Полученная картина называется спиральным вихрем (рис. 247).

Мы могли бы наложить еще продольную скорость, перпендикулярную плоскости течения. Получающуюся картину течения можно интерпретировать двояко: 1) как винтовое движение газа в выхлопной струе и 2) как втекание жидкости в пустой сосуд, если источник заменен стоком.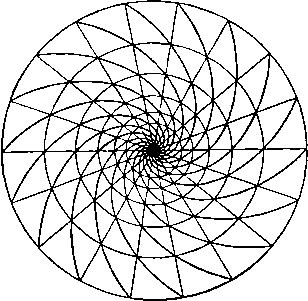

Рис. 247.

13.40. Вихревая нить, параллельная двум перпендикулярным плоскостям. Возьмем в качестве координатных осей линии пересечения перпендикулярных плоскостей с плоскостью течения. Пусть вихрь находится в точке (X, у). Тогда система вихрей, отраженных относительно заданных плоскостей, будет состоять из вихря -X в точке (х, -у), вихря -х в точке ( - - -, у) и вихря X в точке ( - х, -у). В точке, в которой находится сам вихрь, скорскти индуцированы только его отражениями. Эти компоненты скорости показаны на рис. 248. Так как x = rcos9, а t/ = rsin9, то радиальная и трансверсальная компоненты скорости вихря имеют вид

dr xcose xsine X cos 29

dt 2/-sin 9 2rcose г sin 20 dO X xsinO xcosO 2r~

dt 2r 2rsin6 2/-cose 2r

Отсюда, разделив первое равенство на второе, мы получим

1.= 2 cos 20 dO г dt sin 28 dt

Интегрируя последнее выражение, придем к равенству

г sin 20= а,

где а -некоторая постоянная. Форма траектории вихря и направление движения вихря по этой траектории показаны на рис. 248.

XJ2r

Рис. 248.

13.50. Вихрь внутри или вне кругового цилиндра. Пусть вне цилиндра г| = а в точке Z = X-f/К существует вихрь интенсивности х. Если движение жидкости происходит только вследствие этого вихря, то в силу теоремы об окружности мы имеем следующее выражение для комплексного потенциала течения:

/xln(2-Z)-/xln(--Z), (1)

которое с точностью до несущественной постоянной эквивалентно выражению

:х In (z - Z) - /х In z-+ /х Inz.

Отсюда следует (ср. п. 8.61), что система отраженных вихрей состоит из вихря интенсивности -X в точке, сопряженной с данной относительно окружности, и вихря интенсивности х в центре этой окружности.

Если к сумме (1) прибавить член /х1п( -Z), не зависящий от z, то комплексный потенциал течения примет вид

tt = /xln(2-Z)-/xlnl--) = (p + xG, (2)

где функция тока xG постоянна на границе цилиндра и выражается формулой 2ixG=U) -И). Отсюда следует

G = G(2, z;Z, Z)=lnz-Z-lln(l-J)(l--?).

Теперь ясно, что функция G обладает свойством симметрии

G(z, z; Z, Z)=G(Z, Z; z, z),

которое означает, что функция не изменяется при перемене местами пар переменных). Теперь запишем

g(z, z; Z, Z) = G(z, z; Z, Z)-lnz-Z= j In(1 -(1 -. (5) Функция g обладает следующими свойствами:

(I) Функция g(z, z; Z, Z) является гармонической функцией переменных (jc, у), не имеющей особенностей в точке z=Z или в любой точке области, занятой жидкостью.

1) Функция G является фактически функцией Грина.