Если точка О является обыкновенной точкой контура, то 2у = я и касательные служат частями одной линии. Если контур симметричен относительно оси JC, то е = 0.

Если приближаться к точке О вдоль линии Xi, то 6->уЧ-е; но если приближаться к точке О вдоль Я^, то 6- -у + е. Кроме того, когда -gia функция (О (С) стремится к бесконечности; то же происходит при

Единственной функцией, удовлетворяющей этим условиям, является функция

Для доказательства этого рассмотрим поведение следующей функции:

/(0 =

когда точка £ движется внутри или вдоль полуокружности в плоскости С-Если мы определим логарифм так, чтобы 1п/(0) = 2/(а -я), то функция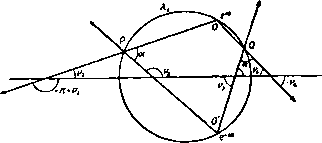

Рис. 233.

In / (С) будет однозначной и аналитической во всех точках внутри полукруга.

Далее, рассмотрим точку С, совпадающую с точкой Р на дуге X, (рис. 233). Мы имеем

arg / (С) = arg (S - е' ) - arg (С - е-* ) =

= -n + \i - \2= -Я -(я -а)= -2я-fa.

Если значение £ берется в точке Q на дуге Я то

arg(C)= - Vi -v,= -я + а.

Таким образом, arg/(P имеет постоянное значение а -2л на линии Я| и постоянное значение а-я на линии Я,. Если величина £ проходит через точку О, переходя с линии Я^ на линию Xj, то arg/ДС) убывает на величину я. Далее, имеем

я 2iy

ln( e-* )-l-ln/(S)

,0,.в-(а-).

Таким образом, мы выделили особенности функции со (5) в точке О и в ее отображении О'. Если положим

(C) = (OoЮ + (D.

где

Q(C) = ao-f а. + агСЧ

то получим общее решение задачи о струйном обтекании препятствия. При этом функция (0(0 имеет один разрыв на полукруге плоскости t,. Задавая функцию Q(C), можно получить те контуры, для которых функции Q(C) будут давать решение задачи. Обратная задача определения функции (оЦ) по заданному контуру является, конечно, более трудной и лишь в немногих случаях она была решена полностью*).

12.50. Решение для случая Q(S) = 0. В этом случае, согласно п. 12.47, имеем

<o(;) = a),(C) = e-Y+ln-f. (1)

Так как в силу п. 12.43 00(0)= О, для определения а получаем

Кроме того, угол 8 имеет постоянное значение вдоль Х, и Хг- Следовательно, функция со (С) соответствует потоку, обтекающему по схеме

Задача о симметричном обтекании дуги круга с отрывом струй впервые была точно решена А. И. Некрасовым в 1921 г. в его работе сО прерывном течении жидкости в двух измерениях вокруг препятствия в форме дуги круга , Собр. соч., т. I, стр 52-69, Изд-во АН СССР, М., 1961.

Обзор основных работ, посвященных отысканию обтекания с отрывом струй заданной криволинейной дуги, можно найти в книгах: Седов Л. И., Плоские задачи гидродинамики и аэродинамики, М., 1950; Биркгоф Г., Сарантонелло Э., Струи, следы и каверны (готовится русский перевод в ИЛ, М.); Гуревич М. И., Теория струй идеальной жидкости, Физматгиз, М., 1961.

Систематическое обобщение метода Кирхгофа для решения весьма широкого класса задач в случае препятствий с прямолинейными стенками дано в известной монографии: Жуковский Н. е.. Видоизменение метода Кирхгофа, Избр. соч., т. I, Гостехиздат, М., 1948. -Ярил, перев.

Но 1п( -е-* ) = /(я -а). Поэтому, если точка I находится на линии X то

8 = е-у+-{/(я-а) + /(а-я)} = е-у, а если точка С находится на линии X то

е = е-у + -{/(я-а) + /(а-2я)} = е +Y-

Кроме того, очевидно, что то(С)-схз, когда -*е* или когда Таким образом, функция обладает всеми требуемыми свойст-

вами. Кроме того, функция й)о(С) принимает действительные значения при действительных значениях С, и поэтому ее можно продолжить на нижнюю половину круга с помощью зеркального отражения. Отметим также, что

Кирхгофа пластинку, согнутую под углом 2у, как это изображено на рис. 234. Так как

iv 5 i(X+<i) ii (X-ot) ii(X-<i)

gtx gia g2 (e2

-e2 ) = 2 е2 sin-2(X -a),

из формулы (1) получим мнимую часть функции в виде

\sin -i(X+a)

Подставляя это выражение в формулу (3) п. 12.44, получаем длины отрезков ОАу, ОА, отсюда заключаем, что эти длины не произвольны. Это

и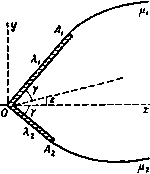

Рис. 234.

означает, что критическая точка расположена на сгибе пластинки только тогда, когда пластинка ориентирована соответствующим образом к потоку. Иначе на сгибе произойдет резкое изменение направления скорости; физически приемлемые решения можно получить путем изменения положения каверны так, чтобы она охватывала или одну часть пластинки, или обе части.

Следует отметить, что небольшое изменение угла у может вызвать сильные колебания положения критической точки и соответственно вибрации пластинки.

Для вычисления подъемной силы находим

я 1 (1-Se )*i

Отсюда получаем

ш'(0)=--sina, ш'(0)=--sin 2а. Здесь величина а задается формулой (2).

Применяя формулы п. 12.46 для нахождения лобового сопротивления и подъемной силы, получим

яе

12.51. Удар потока о пластинку. Если положить 2у = п, то изгиб пластинки исчезает; мы получаем случай потока, ударяющегося о неподвижную пластинку, как это изображено на рис. 213. Тогда из формулы (2) п. 12.50 получаем а = е + /зЯ, так что а является углом, под которым пластинка наклонена к асимптотическому направлению потока в бесконечности. Формулы п. 12.50 для лобового сопротивления и подъемной силы дают тогда результаты, уже полученные в п. 12.26). Когда а = /гЯ, мы получаем результаты п. 12.21.

12.52. Симметричный случай. Если в задаче п. 12.50 положить е = О, то получаем симметричный случай прямого удара о пластинку, согнутую посередине (см. рис. 235). Эта задача может служить моделью струйного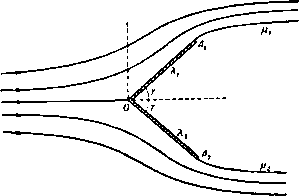

Рис. 235.

обтекания корабля с острым носом. В случае а = Vgit лобовое сопротивление, согласно п. 12.50, равно Аа*фуЧя, а подъемная сила обращается в нуль. Указанная величина содержит константу а, которую можно выразить через /г/ -длину отрезка OAi следующим образом. Так как е = 0, то из формулы (1) п. 12.50 имеем

Отсюда, положив

получим

(S) = 0 + /x = lni±f.

=4-In/,

поэтому формула (3) п. 12.44 дает

I r cosxsinXdX = Sr {- ,,

и

о о

Обозначая величину определенного интеграла через /, получаем

и, следовательно, лобовое сопротивление равно VaeYV(it/).

1) Для проверки этого утверждения надо выразить величину а* через скорость U и длину пластинки /. Детали вычислений объяснены в п. 12.52.

/=2/.(.-i)-/.(.-J).

Далее легко установить следующую рекуррентную формулу:

Пользуясь этой формулой, получаем

и величину / можно вычислить, пользуясь таблицами*) функции Y.

ПРИМЕРЫ К ГЛАВЕ 12

1, Бесконечно широкий поток со скоростью U в бесконечности, параллельной прямолинейному берегу, ударяется об уступ высоты А, перпендикулярный к берегу. Найти свободные линии тока и определить силу, с которой поток действует иа уступ.

2. Поток конечной ширины с имеет скорость в бесконечности с проекциями

(-к'cos а, -И sin а).

Поток ударяется о плоский неограниченный барьер у = 0. Показать, что двумерное безвихревое течение в струе при отсутствии массовых сил определяется формулами

dw Л (/-X) dQ В / 1/

dt it-l) dt (/ Х)(/2-1)/г

где -1<Я,<-Ь1-

Показать, что поток разбивается на две ветви с наибольшими толщинами, равными с cos* 2 с sin- у

Предполагая, что давление иа барьер со стороны, противоположной потоку, равно давлению на свободных линиях тока, показать, что силы, действующие на части барьера по обе стороны от точки с нулевой скоростью, относятся как (я - а): а.

3. Показать, что в случае, когда поток ударяется о пластинку под углом а, критическая точка Делит пластинку иа две части в отношении, равном

24-2со5а--(я-а) sin a-f2 cos а sin* а 2 -2 cosa-t-a sin а -2 cosa sin* а

Отсюда вывести, что критическая точка всегда находится между серединой пластинки и ее концом, более удаленным по отношению к набегающему потоку.

1) Mi Ine-Tiiomson L. М., Calculus of Finite Differences, Lnd., 1959, §9.3.

) British Association Tables, vol. 1. Lnd., 1931 (на русском языке см., например, Лебедев А. В., Федорова Р. М., Справочник по математическим таблицам, Изд АН СССР, 1956.-Яриж. ред.).

Для вычисления / полагаем

О

Тогда

Мл)=1ч'()-1ч'(),

где Y (дс)- логарифмическая производная от Г-функции*). Для функции / имеем

где V-скорость потока в бесконечности.

5. Жидкость из области y=-\-cxi течет между двумя плоскими стенками х = а, У>6 и симметрично ударяется о плоскость у = 0. Объяснить, как можно найти вид свободных линий тока, и показать, что если d-наибольшая ширина потока, ударяющегося о плоскость у -О, то

яа \a-dy

6. Поток конечной ширины ударяется о бесконечное плоское препятствие; предполагается, что движение двумерное и поток ограничен кривыми, вдоль которых величина скорости постоянна. Пусть скорость невозмущенного потока в бесконечности составляет

угол -2-я -а с препятствием. Показать, что расстояние от критической точки на поверхности препятствия до границы потока так относится к ширине невозмущениого потока, как

(l-;-sin а)-f а cos* аsin а cos а In (2 cos а)-) 2 cos а Arth б

Показать, что результирующие величины давлений, действующих на каждую из двух частей препятствия, разделенных критической точкой, относятся как (л-Н2а) : (л-2а).

7. Поток несжимаемой жидкости, имеющий в бесконечности скорость U, ударяется симметрично о согнутую пластинку. Поперечное сечение пластинки состоит из двух прямолинейных отрезков, образующих прямой угол. Длина каждого отрезка равна а. Поток омывает пластинку с выпуклой стороны, а за пластинкой с внутренней стороны ограничен двумя свободными линиями тока. Показать, что результирующая величина давления на пластинку равна >2 леа{*/{б )/24-я--2 1п (> 2-1)} и что в естественных координатах уравнение каждой из свободных линий тока можно представить в виде s = i4ctg2 2e, где j4 -константа; s -длина дуги, измеряемая от края пластинки, ив -угол, образуемый касательной свободной линии тока с осью симметрии.

8. Перпендикулярная к плоскости ху согнутая пластинка, поперечное сечение которой состоит из двух прямолинейных отрезков АВ и ВС, образующих прямой угол между собой, помещена в поток несжимаемой жидкости. Поток имеет в бесконечности единичную скорость, направленную в сторону отрицательной оси Ох, так что центральная линия тока является прямой, совпадающей с осью Ох, встречающей пластинку в точке В с выпуклой стороны и делящей пополам угол ABC. Применяя обычные обозначения, показать, что всем условиям течения можно удовлетворить, положив

qln V(t~<)(c-b)+V(c-t)(b-a) ,

V{.t-b)(c-a)

Выбирая масштаб измерений так, чтобы с-а = 1, и полагая с-1 = соъЧ1, показать, что справедливы равенства

L = 2 s\n{UB)s\n(U-B)s\n2UdU, н

Я=2 ъin(U-B)iin(U-B)s\n2U dU,

4. Показать, что преобразования

dl i(i~VyHl+VY

приводят к решению задачи о пластинке, расположенной наклонно в потоке жидкости, ограниченном с обеих сторон свободными линиями тока.

Если 26-ширина пластинки, а -угол ее наклона к потоку, то показать, что выполняются соотношения

2bV ,а , 2bV . . а cos<-, х'=- sin*

Примеры 331

где в -значение U при / = 6; L-длина половины пластинки; Р-результирующая величина давления на пластинку.

9. Доказать, что в случае потока, изображенного иа рис. 234, длина омываемой части пластинки Xi задается формулой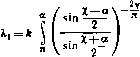

(cosX-cosa)sinXdX,

а формула для части пластинки Я? получается путем замены на нуль нижнего предела в последнем интеграле. Исходя из этого, показать, что если длина Xi задана, то имеется только одно значение длины Xj, при котором рассматриваемое здесь течение возможно.

Глава 13 ПРЯМОЛИНЕЙНЫЕ ВИХРИ

13.00. в этой главе рассматриваются некоторые вопросы двумерного вихревого движения жидкости. При таком движении вектор вихря направлен всегда перпендикулярно плоскости движения. Мы, как обычно, рассматриваем слой жидкости единичной толщины, т. е. предполагаем, что жидкость ограничена двумя плоскостями, параллельными плоскости движения и отстоящими друг от друга на расстояние, равное единице длины. Вихревыми линиями являются прямые, параллельные друг другу; все вихревые трубки являются цилиндрами, образующие которых перпендикулярны плоскости движения. Такие вихри называют прямолинейными вихрями. Как и прежде, мы будем использовать понятия плоской геометрии.

13.10. Круговой вихрь. Пусть в безграничной жидкости имеется цилиндрическая вихревая трубка, поперечным сечением которой является круг радиуса а.

Сечение вихря плоскостью движения представляет собой круг, следовательно, такое течение можно рассматривать как круговой вихрь (рис. 236).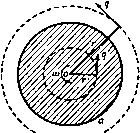

Р н с. 236.

Рис. 237.

Мы будем [предполагать, что завихренность в области, ограниченной окружностью этого круга, имеет постоянную величину со. Вне окружности завихренность равна нулю. Проведем окружности радиусов г' и г, концентрические с той, которая ограничивает вихрь, причем г' < а < г (рис. 237). Пусть q и q - скорости движения жидкости на окружностях с радиусами г' и г. В силу симметрии ясно, что скорости любых точек на окружности одинаковы по величине и направлены по касательным к этой окружности. В противном случае радиальные составляющие скоростей давали бы расход через окружность, а в ее центре О должен был бы быть источник или сток. Аналогично этому скорость в любой точке на окружности г направлена по касательной к ней.

Применим к этим окружностям теорему Стокса о циркуляции (п. 2.50). В результате получим равенства

q ds= тяг'*, если г' < а, \ qds= сояа', если г > а.

Так как величины д' а q постоянны на соответствующих окружностях, то мы получаем

2лг9= тлг'*, 2пгд = (опа^.

Отсюда следует, что q = Угшг при г' <. а; q = Уга- при г > а. Когда

/ = г = а, мы имеем q = q = Угат, т. е. скорость непрерывно меняется при переходе через окружность радиуса а.

Таким образом, оказывается, что описанный нами вихрь образует некоторое поле скоростей. Это поле скоростей, вызванное вихрем, называется индуцированным полем скоростей, а скорость любой точки поля называется индуцированной скоростью.

Обычно скорость в некоторой точке поля называют скоростью, индуцированной вихрем, но это название следует понимать как удобное сокращение следующего более полного утверждения: если бы в жидкости существовал только один этот вихрь, то скорость в точке имела бы такую величину. В этом смысле, когда существует несколько вихрей, поле каждого вихря будет вносить свой вклад в величину скорости в рассматриваемой точке.

Возвращаясь к круговому вихрю, рассмотрим точку, расположенную вне вихря, причем радиус-вектор этой точки, проведенной из центра вихря, имеет величину г. Тогда оказывается, что индуцированная скорость обратно пропорциональна г и перпендикулярна радиус-вектору. Таким образом, индуцированная скорость стремится к нулю, когда модуль радиус-вектора точки стремится к бесконечности.

Что касается жидкости внутри вихря, то ее скорость пропорциональна г и, следовательно, жидкость внутри вихря движется, как твердое тело, вращающееся вокруг точки О с угловой скоростью /j (О. В центре вихря скорость равна нулю. Этот важный факт может быть установлен следующим образом.

Круговой вихрь не индуцирует скорости в своем центре. Это утверждение следует понимать так: центр кругового вихря, существующего в покоящейся жидкости, остается неподвижным.

Из вышесказанного следует, что скорости точек, лежащих на концах некоторого диаметра внутри вихря, равны по величине, но направлены в противоположные стороны, так что средняя скорость жидкости внутри вихря равна нулю. Таким образом, если круговой вихрь малого радиуса помещен в точку некоторого потока, где скорость равна и, то средняя скорость в его центре будет равна и и жидкость, заключенная в вихре, будет двигаться со скоростью и; это означает, что вихрь движется вместе с потоком жидкости.

Примерами круговых вихрей в природе могут служить тропические циклоны (ураган, тайфун), которые достигают в диаметре) от 100 до 500 миль и перемещаются со скоростью, редко превышающей 15 миль в час. Внутри циклона ветер может достигать ураганной силы, в то время как существует центр области диаметром от 10 до 20 миль, где условия могут быть относительно спокойнее.

Из полученных выше результатов мы можем вывести следующие формулы:

а

если г<а, - = у, если г > а.

2 2 °

откуда следует, что скорость q стремится к нулю на бесконечности и максимальна на границе вихря.

На рис. 238 графически иллюстрируются последние формулы. Заметим, что кривая на этом графике является частью гиперболы.

М Brunt D., Weather study, London, 1942.

Вне вихря движение является безвихревым, а скорость задается выражением qe ( +! ), так что

1 . аЧ)

dz г i Z

Интегрируя это соотношение, находим комплексный потенциал

Отсюда видно, что существует циркуляция интенсивности ша*.

Следовательно, величину х мы можем назвать интенсивностью вихрядействительная циркуляция будет тогда равна 2ях.

Таким образом, комплексный потенциал течения жидкости вне вихря интенсивности х, центр которого находится в точке Zo, задается формулой

ш=1х1п(2 -го).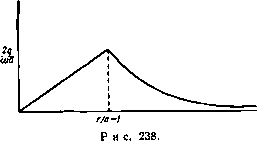

г/а

13.11. Давление в поле кругового вихря. Обозначим через pi я р соответственно давление внутри и вне вихря. Давление должно быть непрерывно на границе вихря, следовательно,

Pi = p при г = а. (1)

Внутри вихря уравнение движения жидкости имеет вид

1 dpi гсо* х*г

так как жидкость вращается с постоянной угловой скоростью 00/2, следовательно, ускорение жидкости равно гсо*/4 и направлено к точке О. Интегрируя последнее уравнение, мы получаем формулу

где Ро -давление в центре вихря.

Вне вихря мы можем использовать уравнение для давления в виде

П

2л. const = -,

1) Это обозначение позволяет избежать повторения лишнего множителя 2я, подобное обозначение было введено при определении источника в п. 8.10.