Соответствующая область в комплексной плоскости Я изображена на рис. 223.

Все константы можно определить, устанавливая взаимосвязь между точками, соответствующими точкам А, В, С ъ разных плоскостях. Если 2/ -ширина отверстия, то мы получим

А, = л/2, 2 = ii, оу = 0 в точке Л,

Я = я в точке В, Я=я (-/аэ, 2= -f аэ в точке С;

отсюда, учитывая равенство К = Ш, получаем

С

2Ш , . , 2li

InSinA, 2 =

л + 2

==/tyctg4-.

Рис. 223.

Для определения положения точки В* положим Я = 0; тогда для z получим значение 2я /(л +2).

Ширина струи в бесконечности равна половине модуля этой величины, т. е. я (л + 2); отсюда коэффициент сжатия равняется я/(я4-2) =0,611.

Для получения уравнения свободных линий тока в выражении для z полагаем Я = я/2 + iv. Тогда

x=-{v-ihv), г/ = -(5сЬу+я/2), 0<у<оо.

12.33. Поток, ударяющийся о пластинку. Эта задача была рассмотрена б п. 12.20. Для применения метода отображений достаточно рассмотреть

Л'ПЛоааст

Рис. 22-1.

половину потока. Соответствующее отображение потока показано на рнс. 224.

Заметим, что в точке А* угол равен Зя/2 и является отображением угла л 2 в точке А. Отображением линии АЕса является параллельная ей прямая Л*£.

Пусть ds и ds* -соответственно элементы дуги АВ и ее отображения А*В* (т. е. А*В). Тогда из формулы (4) п. 12.30 мы получим ds* = dayVt/*; так как на АВ скорость q изменяется от нуля в точке Д до t/ в точке В, то отрезок i4*B* короче отрезка АВ (рис. 225).

(Отображенный поток частично перекрывается с исходным потоком, и поэтому его следует рассматривать на отдельном листе поверхности Римана.

Для определения формул отображений имеем

Подстановка = -cosЯ дает

= - Lcos Я, (1 -t-cosX),

Здесь мы положили, что w=0 в точке В, т. е. при =0, и что z = 0 в точке А. Из формул (1) и (2) находим

dw/dz = -15 = 2К sin K/{L (1 + cos \)).

w-плоскость

С

-плоскость

Х-пласкасть

Рис. 225.

В точке В имеем Х = я/2, z = /, i3 = i/, здесь 2/- ширина пластинки Отсюда

Я+4

Окончательно

ш = со8*Я, z = - (-X + sinX-l--i-sin2x).

В точке А*, где Х = я, величина г равна 2я (я4-4). В п. 12.22 было найдено, что коэффициент лобового сопротивления равен 2я/(я--4). Схюг-ношение между этими значениями не является случайным, как сейчас будет показано.

12.34. Геометрическая интерпретация силы, действующей на препятствие. Рассмотрим поток, обтекающий препятствие АВ. Пусть ВСоо -свободная линия тока (рис. 226). При отображении относительно линии ВС образом дуги препятствия будет линия Bi4*. Пусть вектор X-\-iY = F является силой, действующей на единицу толщины препятствия. Тогда, согласно п. 6.41, имеем

в

f = J -i(p-Pc)dz,

здесь рс-давление в каверне. По теореме Бернулли находим

отсюда в силу формулы (4) п. 12.30 получаем

в в

F = \qUH-i) \ (l dz=-QW{-i) \ (dz-dz*) =

л А

= -д£/ /(а*-а).

где а* и а - комплексные числа, соответствующие точкам А* к А.

Таким образом, результирующая сила по величине и направлению такая же, как если бы избыточное давление застойной области действовало вдоль всей линии, соединяющей точки А и А*.

Если тело и поток симметричны, то сила совпадает с направлением потока и прямая линия А А* перпендикулярна к этому направлению. Б этом случае величина силы равна ViqUAA* и коэффициент лобового сопротивления равен АА* /АВ, как показано в этом пункте.

12.35. Обратная струя. Возможный тип каверны, наблюдаемый при входе препятствия в жидкость, состоит в том, что непосредственно за препятствием об- р и с. 226.

разуется струя, направленная в сторону

препятствия; позади струи возникает критическая точка потока. На рис. 227 изображен такой симметричный поток, обтекающий согнутую пластинку; при этом свободные линии тока, как обычно, показаны пунктиром; точка Е является критической.

Математически обратную струю можно рассматривать как простирающееся до бесконечности воображаемое продолжение набегающего потока, но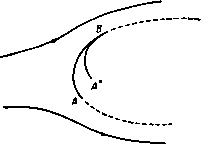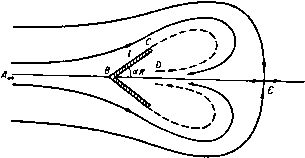

Р н с. 227.

уже переходящее на второй лист плоскости потока. В действительных потоках обратная струя может разрушаться, не достигнув препятствия, или может сначала удариться о препятствие, а затем исчезнуть.

Рассмотрим только верхнюю половину потока и отобразим эту часть потока и ее отображение на верхнюю половину плоскости £. Плоскости ш и С показаны на рис. 228.

ш-птиикин ЛВС 0

-в -а -1 {О t а в

i-плоскости .пвшаввва--

е А В С В' Л' Е'

Рис. 228.

в точке В равен (1-а)я, в точке В* угол равен (14-а)я, в точках Л^, и А^ углы равны -я, а в точках Е и Е* равны я и Зя соответственно.

В плоскости W отображение является простым зеркальным отражением относительно прямой CD и поэтому

Комплексная скорость имеет вид

Константы К, L, a, e можно определить из следующих пяти условий:

о

(I) Если ВС=1, то Ie = zc-ZBК \ 1.

(II) Мы обозначаем через 2а+ предельное значение г при приближении к точке А справа вдоль действительной оси плоскости Аналогично через 2а- обозначим предельное значение z при подходе к точке А слева. Тогда имеем, что /т (гд-) -/т (2+) =0, так как

1т {ZA-) - Itn (2a+) = Im (nir),

где г - вычет функции dz/d при Z = -

(III) Функция W вблизи точки С принимает действительные значения, так что величина L - действительная.

(IV) Скорость Уд = -V, где V - скорость на свободной линии тока.

(V) Скорость va = и, где (У - скорость потока в бесконечности.

Эти условия позволяют выразить константы К, L, а, е через величины V, и, I; при этом все интегралы вычисляются в явном виде). Величины V и U

) Рассматриваемый здесь поток был исследован другим методом Гилбаргом и Роком (G i I barg D., Rock D. Н., Naval Ordnance Laboratory Memo. 8718, 1945).

[Рассматриваемая здесь схема течения была также предложена в работе Д. А. Эфроса Гидродинамическая теория плоско-параллельного квазистационарного течения , ДАН СССР, 51, № 14 (1946). Соответствующая задача для случая 0 = 1/2 была решена М. И. Гуре-вичем в статье сОб одной схеме струйного обтекания плоской пластинки , Труды ЦАГИ, № 612 (1947).-Ярил, перев.]

Пусть ая - угол наклона части ВС пластинки к направлению потока в бесконечности и пусть точки В, В* соответственно отображаются в точки t, = = -1,1, а точки Е, А, £*, Л* - в S = -е, -а, е, а. Тогда мы имеем

При получении этой формулы было учтено, что, согласно принципу отображения, угол с вершиной С в плоскости z равен 2л, угол с вершиной

связаны соотношением

где П - давление в бесконечности, - давление в каверне. Применив метод п. 12.34, находим, что коэффициент лобового сопротивления равен Угп К .

12.40. Метод Леви-Чивита. Изложим теперь общий метод построения течения, обтекающего препятствие. Предполагается, что течение установившееся, безвихревое, двумерное и что каверна образуется за препятствием. Существенной чертой данного метода является отображение области плоскости W на внутренность единичного полукруга плоскости при котором свободные линии тока переходят в диаметр полукруга. Далее в методе используется функция (О (О, которая уже была применена в теории струй (п. 11.11).

12.41. Отображение плоскости г. Предположим, что препятствие S расположено в бесконечном потоке, имеющем скорость U в бесконечности (рис. 229).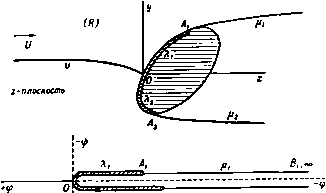

А

(-W)-плоскость I I

Л, ft, g ~

W-плоскость

JiL.

Z-плоскость

-cos a

плоскость

Jj fit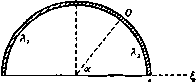

f> 0- ft,

P и с. 229.

Одна из линий тока v, идущая из бесконечности, подходит к препятствию по направлению его нормали (в критической точке О); здесь она разветвляется, следуя далее по препятствию вдоль дуг Я, и Яг, и затем покидает тело в точках

где

Z(W, + Wt) + ~ (Wi-Wt)= а {Z +cos а),

Заметим, что точка И' = 0 соответствует значению Z= - cos а.

Отобразим теперь верхнюю половину плоскости Z на внутренность полукруга плоскости С. радиус которого равен единице, центром которого служит начало координат и диаметр которого направлен по оси х, как изображено на рис. 229.

Необходимое преобразование является преобразованием Жуковского

Для того чтобы убедиться в этом, на дуге полукруга положим t = 6* ; тогда Z= - cosX. Следовательно, когда % изменяется от О до я, точка описывает полуокружность, а величина Z изменяется от - 1 через значение-cos а до 1. Дуга полукруга соответствует отрезку А1А2 действительной оси плоскости Z; дуга Л,0 соответствует линии а дуга Л2О -линии А,2. С другой стороны, когда t, изменяется от -1 через О до Ч-1, величина Z изменяется от 1 до оо и затем от - оо до -1. Таким образом, радиусы OAi, О'Аг будут соответствовать линиям р , р.. Так как при конформном отображении направления обхода не меняются, то верхняя полуплоскость Z перейдет во внутренность полукруга.

Исключая величины Z и W, получаем следующую формулу:

cosa-l-(S-f )J,

которая дает конформное отображение области плоскости w на внутренность полукруга. Кроме того, критическая точка О соответствует значению

Ai Ai, переходя вдве свободные линии тока p.i и Цг. между которыми расположена каверна. Положим в точке О ф = О, ф = О, так что разветвляющейся линии тока будет соответствовать значение ф = 0. Начало координат возьмем в точке О, ось х направим по потоку параллельно скорости потока в бесконечности. Область, занятую движущейся жидкостью, обозначим через R.

Для удобства здесь рассматривается диаграмма переменного (-w) вместо W, которая и изображена на плоскости (-ш). Линии р + Я цг + 2 совпадают с положительной действительной осью; они, как и в других подобных случаях, изображены в виде двух слегка разделенных кривых. Область плоскости (-w) отобразим на верхнюю половину вспомогательной плоскости W с помощью следующего преобразования, легко получаемого по теореме Шварца - Кристоффеля:

w= -W .

Точки, соответствующие точкам At и А2, обозначены через Wi и -W2-

Для этих точек имеем Wi = V{-4>i), = V (-фг). где фь фг - значения потенциала скоростей в точка Ai, А г.

Далее, верхнюю половину плоскости W отобразим на верхнюю половину плоскости Z, так что точке А i будет соответствовать значение Z= 1, а точке Л 2 - значение Z = - 1. Как легко убедиться, необходимое преобразование имеет вид

12.42. Линии тока. Для функции тока имеем 21ф = ш -ш = а* cosa -l-(-f-- -а* cosa-1-(с+ -) =

Кроме того,

=ы-ч

Отсюда находим, что уравнение линии тока ф = 0 имеет вид {2со8аа + Л^)-(* + лМ 1)} т,( + л*-1) = 0.

Рассмотрим подробнее это уравнение. Так как линия ti = 0 соответствует диаметру полукруга, а линия I + ti*-1 =0 -его окружности, то составная линия является разветвляющейся линией тока; уравнение оставшейся кривой дает кубическую кривую

ia* + + l)-2cosa(g* + V) = 0,

которая проходит через критическую точку О (cos а, sin а) и касается оси Ti в начале координат. Мы рассматриваем только ту часть этой кривой, которая расположена внутри полукруга. Эта кривая изображена на рис. 230; вид линий

был определен по методу п. 6.23. Рис. 230.

12.43. Функция <i)(g). Функция со (Р определяется уравнением

qe-ii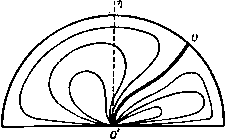

и

Таким образом, имеем

а)(р = 0 + /1п-=е+/т.

Спедовательно, 6 - действительная часть функции со (J) - определяет угол между вектором скорости жидкости и осью х в плоскости г, а мнимая часть т определяет величину скорости, так как

q = (/е*.

На свободных линиях тока q = U, поэтому т = 0.

Таким образом, функция со (С) па линиях р р^, т. е. на действительной оси плоскости принимает действительные значения. Кроме того, в-О в бесконечно удаленной точке плоскости z и поэтому

(О (0) = 0.

Функция со (р должна быть аналитической функцией во всех точках внутри полукруга, так как они соответствуют области R плоскости z, где движение непрерывно. Кроме того, мы видели, что функция со (С) принимает действительное значение на действительной оси плоскости £. Поэтому функцию можно продолжить (см. п. 5.53) на вторую половину еди-

ничного круга, давая этой функции значения m ( в точках 1, и, следова-

тельно, в симметричных точках значения не изменяются. Изменяется только знак у величины т. Функция ш ((), как мы теперь покажем, определяет все свойства движения.

12.44. Фиксированные линии тока. Рассмотрим линии тока Xj, Xi (см. рис. 229), совпадающие с границей обтекаемого тела. Они изображаются дугами /4,0, А2О в плоскости С- Теперь из определения функции (0(5) и из выражения функции w через С (п. 12.41) мы получаем

Udz= -e* >dtt)=aV (c+4--2cosa) (\--L. (1)

Далее, на дуге Л^О мы имеем

Подставим это выражение в формулу (1) и проинтегрируем по х от Х=а до некоторого значения % на дуге OAi; учитывая, что точка О соответствует значению z = О, получаем в результате

Uz= - 2а' е* (cos х - cos а) sin х dX- (2)

а

Сравнение действительных и мнимых частей в этой формуле дает

д: = - е- cos 9 (cos % - cos а) sin х dx,

а

у-= - e-sin8(cosx -cosa)sinxdx a

Полученные уравнения представляют собой параметрические уравнения омываемой стенки Я], если изменять х от О до а, и стенки Я если брать значения х в промежутке от а до я.

В частности, если в формуле (2) положить х = 0> то получим значение 2j, соответствующее точке А^.

Если через dk обозначить элемент дуги Я1 или Яг, то имеем

и dX = U\dz\ = 2а е- cos х - cos а j sin х dx

и поэтому

а

wS e-cosx-cosa)s\nxdx- (3)

Здесь нижний предел О соответствует дуге Я а нижний предел я -дуге Я так как dx является отрицательным при изменении х от я до а, то и разность cos X -cos а будет того же знака.

Радиус кривизны г омываемой стенки выражается формулой

-§ = -l<=oX-cosaisiпxl. (4)

12.45. Свободные линии тока. Параметрические уравнения свободной линии тока \it получаются интегрированием уравнения (1) п. 12.44 по С от С = I до С = 5. где -точка на дуге О'А^. При этом надо учитывать, что в точ-

ке Аг величина г принимает значение 2, найденное в п. 12.44. Таким образом, получим

и

(. ,=4f .(: + 2cc,s )(£-)f .

где £ -действительная величина. Сравнение действительных и мнимых частей в этом уравнении дает искомый результат.

Комплексная скорость задается выражением

Давление. Воспользовавшись уравнением для давления и обозначив через П давление в каверне, получим

Таким образом.

Эта формула выражает гидродинамическое давление.

12.46. Лобовое сопротивление, подъемная сила и момент. Пусть результирующая сила, действующая со стороны жидкости, имеет компоненты X, Y вдоль осей координат, имеющих начало в точке О плоскости г. Тогда, согласно теореме Чаплыгина-Блазиуса, имеем

X + iY = i J (p-i{)dz = -QU 5 {\-e)dz.

UxOAt) (AlOAt)

Так как Udz= - е**><Е)йш, то отсюда получаем

X + iY-QU 5 e* (t)-dC-{Qt I e-<C)+2tdC.

(AiOAi) (АгОАО

Здесь интеграл берется по дуге полукруга в плоскости

Рассмотрим теперь аналитическое продолжение (см. п. 5.53) функции w{t,) на всю область внутри круга Г, изображенного на рис. 231.

Имеем

ш (I) = / (в - ix) = / (6 + it) -f 2т = ш (С) + 2т.

С другой стороны, величина w принимает действительные значения, когда £ описывает дугу AtOAt (см. рис. 229) и поэтому dw = dw. Кроме того, когда £ описывает дугу AiOA окружности круга Г против часовой стрелки, то g описывает дугу /4,Pi4, по часовой стрелке. Таким образом, мы имеем

Рис. 231. ei<o(i)Jdl =

(AjOA,)

(AlPAi)

Следовательно, остается вычислить вычет подинтегральной функции относительно единственного внутри круга Г полюса; этот полюс находится в точке С = 0-

Применяя разложение в ряд Маклорена и учитывая, что й)(0)=0 (п. 12.43), получаем

Кроме того.

еш(С) = 1 + ,Ха) (0) + 4 V Iffl (0) - ((О' (0))*J + .. . .

Перемножив эти два выражения и выделив в результате коэффициент при 1/S, находим вычет в следующем виде:

-i а iw (0) - 2/ cos aw (0) - -[ [ш' (0)]* .

Таким образом, применяя теорему о вычетах, мы имеем

X + iY = nqUa* {w (0)) + nQUa4 [4w (0) cos a-w (0)],

X = 4 (0)1*. y = \ noUa [4w (0) cos a - 0) (0)1,

где X -лобовое сопротивление, К-подъемная сила. Эти изящные результаты принадлежат Леви -Чивита.

Момент М действующих сил относительно критической точки О находится с помощью аналогичных вычислений и равняется действительной части следующего интеграла:

M + iN = QU \ г{

(АфАх)

который берется по полуокружности А^ОАх в плоскости С и который должен быть вычислен в каждом частном случае. Знание величин X, Y, М

позволяет методами статики найти одну силу, эквивалентную действию жидкости на препятствие. Эта сила всегда существует, если только X и Y не равны нулю.

12.47. Точка разрыва функции

<л{1). Функция w(l) = Q-\-iT имеет разрыв в критической точке О, так как ее действительная часть 6 имеет в этой точке два значения, соответствующие двум направлениям потока вдоль касательной в точке О; кроме того, т- -00 при приближении к точке О, так как точка О является критической и скорость в этой точке обращается в нуль.

Пусть в точке О касательные к контуру, препятствия образуют между собой угол 2у, как это изображено на рис. 232, и пусть внутренняя биссектриса этого угла составляет угол е с осью х.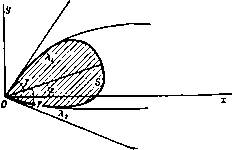

Рис. 232.