е. С

отобразим верхнюю половину плоскости ш* иа верхнюю половину плоскости при этом а, р, б - соответствующим образом выбранные действительные константы (константы действительны, так как при отображении действительные оси соответствуют друг другу). Подставляя £ из формулы (1) в формулу (2), получаем следующую формулу для отображения плоскости на плоскость годографа:

где G, е, т) являются константами. Так как в точке М имеем ш = 0и1з = У, тов.

принимает вид {у? -У*)*. В точке Сш имеем ш=-оо и u = f/, так что

т,= -((/*-Ы^*)/1 . Таким образом, в знаменателе получим выражение

( *-(/ ) (v-lW. Следовательно, мы можем написать

Заметим, что в силу формулы (1) п. 12.10

С-члвелосл

Рис. 210

- 2. Таким образом, числитель

Y1. и*

аЬ= 1.

1-fa

где о -число кавитации.

Формула (3) дает соотношение между w и dwidz и, таким образом, сводит решение задачи к квадратуре.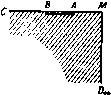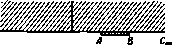

ш-плоскост

М

ю'-ялоскость

Рис. 211.

Применяя обозначения эллиптических функций'), напишем t = v/V = bnd (и\т).

здесь ш -квадрат модуля, mj - дополнение до квадрата модуля. Значения комплексной скорости v в точках М, С, А, В равны соответственно I, U, iV, О, и, следовательно, соответствующие значения величины и равны

4-/С. 0. ±К + 1К'. iK.

Поэтому область в комплексной плоскости и имеет вид, изображенный иа рис. 212.

Из формулы (3) после некоторых преобразований получаем

G{m}/ nd u -l)nd u

-- - (b)

msnucnu

) Относительно обозначений см. работу Милн-Томсоиа, на стр. 227. Уиттекер Э., Ватсо и Дж., Курс современного анализа, ч. II, Физматгиз, М., 1963.

Теперь имеем

dz/du = (dwldu): (dwjdz) = - (dw/du): v, и поэтому в силу формул (5) и (6) находим

(dsu+mj/sdcu).

Отсюда путем интегрирования получим

f(u) + H,

/(u) = Dsu+ml/ Dc , (8)

здесь Я-произвольная константа, Ds , Dcы - эллиптические интегралы второго рода в обозначениях Невилля*). Константы G и Н определяются

условиями

z = h + il при и = Л-К- iK, z = h при u = iK.

в плмяатт

Рис. 212.

где 21 - ширина пластинки и 2Л - расстояние между пластинками.

Обозначим через Со (о) коэффициент лобового сопротивления одной пластинки как функцию от числа кавитации о. Можно доказать, что при малых а приближенно выполняется равенство

CD(o) = (l+a)Ci,(0),

значение числа кавитации о = О соответствует бесконечно большому значению А, т. е. случаю, когда одна из пластинок удалена в бесконечность. Тогда, согласно п. 12.22, имеем

С1,(0)-2я/(я+4).

Так как на практике приходится иметь дело с малыми числами кавитации, то схема Рябушииского приобретает важное значение благодаря удобству ее применения в случае переменных, но малых чисел кавитации *).

12.25. Скольжение и глиссирование. Эта задача возникает при изучении поведения на поверхности воды гидроплана, быстроходных судов и в других подобных случаях.

При скольжении и глиссировании по свободной поверхности давление вдоль свободной линии тока близко к атмосферному (оно постоянно), а число кавитации практически равно нулю.

Прн скольжении вблизи свободной поверхности силой тяжести можно пренебречь, если обе величины gl/U* и gh/U малы по сравнению с единицей; здесь / - длина движущегося тела и А - глубина жидкости.

Однако при расчете брызговой струи, создаваемой телом, движущимся вблизи свободной поверхности в случае глубокой воды, эффектом силы тяжести пренебрегать нельзя. В самом деле, можно получить целый ряд различных течений жидкости, например при движении пластинки с заданным углом наклона и заданной скоростью.

Ниже, в п. 12.26, будет рассмотрена задача, которая возникает при следующих условиях. Пусть задана глубина воды, скорость течения и положение пластинки. Тогда существует наибольшая высота кромки над свободной поверхностью воды (впереди по движению пластинки), при которой возможно

1) Neville Е. Н., Jacobiin elliptic functions, 2-е издание, Оксфорд, 1951, гл. 14.

непрерывное обтекание пластинки. Иначе, допустим, что установилась брыз-говая струя около пластинки, погруженной в поток; тогда эта пластинка может быть выдвинута выше уровня жидкости без нарушения непрерывности струи. Работа, изложенная в п. 12.26, касается формы струи при аналогичном движении на очень глубокой воде.

12.26. Глиссирование пластинки по поверхности потока). Рассмотрим изображенную на рис. 213 неподвижную пластинку ВВ ширины /, на которую набегает поток бесконечной глубины со скоростью U в бесконечности. Предполагается, что у задней кромки пластинки в точке В поток сходит по свобод-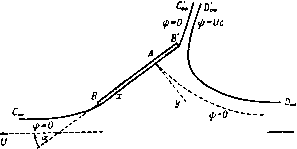

г-плосиость

шппоскость

С- f-0 в

5-плосипсть f -ь \ ? -q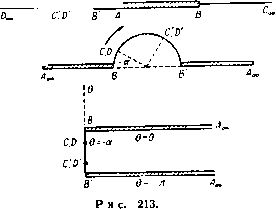

0-пяасиас1па

ной поверхности вдоль линии тока ВСов, а у передней кромки в точке В' образуется струя воды. Эта струя ограничена свободными линиями тока В'С'а,

) G ге е п А Е., Ргос. Comb- Phil. Soc, 32 (1936). [Впервые эта задача была решена в работе Гуревнча М. И. и Ям польского Р., О движении глиссирующей пластинки , Техника воздушного флота, № 10 (1933). Конечность глубины учтена в работе Ю С. Чаплыгина, Глиссирование плоской пластинки бесконечного размаха по поверхности невесомой жидкости конечной глубины , Прикл. мат. и мех., V, вып. 2(1941). Действие силы тяжести учтено в работе: Седов Л. И., Плоская задача о глиссирова-иии иа поверхности тяжелой жидкости. Труды конференции по теории волнового сопротивления, ЦАГИ (1937). Числовые расчеты см.:Чаплыгии Ю. С, Труды ЦАРИ, 506 (1940).-Ярил*, ред.]

так что

A,ch!+ = l (-).

и DoeDaj. Область за пластинкой между линиями ВС и В'С'а, занята атмосферным воздухом при давлении П, такая же область находится выше и правее линии DooD . Следовательно, вдоль всех этих свободных линий тока величина скорости постоянна и равна U - скорости потока в точке Doo.

Существует линия тока, которая встречается с пластинкой в некоторой точке А и разделяется иа две свободные линии тока ВС и В'С„. Предположим, что эта разветвляющаяся линия тока отвечает значению ф = 0. Выберем начало координат в точке А и ось х направим по линии АВ. Предположим также, что направление потока в бесконечности составляет угол - ас отрезком АВ.

Если с - ширина струи в бесконечности, то вдоль линии D , мы должны иметь ф = i/c.

Диаграмма течения в плоскости ш показана на рис. 213, который следует сравнить с рис. 207. Отобразим область плоскости ш на верхнюю половину плоскости ;, ставя точкам В', В в соответствии значения J = -1, +1, а точкам А, С -значения = -а, -Ь. Так как многоугольник на плоскости W имеет внутренний угол в вершине А, равный 2я, и в вершине С' , равный О, то преобразование Шварца - Кристоффеля дает

так что

w = Kt-K(b-a)\n(l; + b) + L.

При обходе вокруг точки С = - 6 в плоскости С аргумент величины d + b) убывает от я до О и поэтому величина In + убывает на in; таким образом, функция ф (мнимая часть ш) убывает на величину К {Ь - а) я. Но при обходе вокруг точки С, как показывает диаграмма на плоскости ш, функция ф убывает от значения Uc до 0. Таким образом, находим

Рассмотрим теперь поведение функции- £/dz/da>, когда точка г описывает контур ABCcoDcoDcoCcoBА. Вдоль свободных линий тока величина скорости постоянна. Следовательно, соответствующий контур, описанный на плоскости, будет иметь вид, изображенный на рнс. 213; величина аргумента при этом убывает от О до -я.

Соответствующая область в плоскости Q изображена на том же рисунке. Для получения отображения этой области на плоскость С используем преобразование Шварца - Кристоффеля, которое дает

dQ Ко

dl (б--а)/(4*-1)

так что

Q=/CArchi-hZ., Ko=KVW).

В точках В', В функция Q принимает значения -(я. О, а величина С принимает значения -1, 1. Поэтому имеем

-Jя = CArch(-l) + L, 0=/CArch(l)-t-Z-.

Таким образом, получим

L = 0, К'=-1 и Q= Archi±,

Движение по схеме Гельмгольца 309

Отсюда находим

dw i/71+ШУ i

Здесь перед квадратным корнем взят отрицательный знак, так как dw/dz = О в критической точке Л(£= - о).

Из последней формулы получаем

Udz 1+а^+Г{1-а*) (1-е*) ,оч

-diT---

Теперь можно найти значение а, учитывая, что в точке Da, имеем - Udz/dw = e-* (рис. 213) и С= - з. Таким образом, формула (3) дает

отсюда а = cos а, так как е-* = cos а -j sine. Кроме того, из формул (1) и (3) получаем

dz К i+al+V(l-a*)(\-t*)

Интегрируя это выражение по С от £= - 1 до S=l, после некоторых преобразований получаем следующую формулу для ширины пластинки:

/ = Vi+- (2а+ (аЬ- 1) m-l) . (4)

Для величины полного давления Т на пластинку, как и в п. 12.21, получаем выражение

Вывод этой формулы предоставляем выполнить читателю. При больших значениях b приближенно находим

cg{/*sina 26(6-0)

Сила Т перпендикулярна к пластинке; поэтому ее можно разложить на лобовое сопротивление D и подъемную силу L; тогда

D=rsina, L = r cosa.

Комбинируя формулы (4) и (5), получаем соотношение

= 2М*-1/1 + (2а + (.*- 1) In.

Отсюда, считая, что величина b велика, можно найти следующее разложение в степенной ряд:

)}+1г^{+ -Ч-- )}

Если в последнем выражении считать, что &->оо, то получаем формулу Рэлея

Так как при Ь-*- оо точки О и О сливаются, то эта формула дает величину полного давления на пластинку, когда неограниченный поток под углом о

ударяется о пластинку, набегая на нее и обтекая ее с отрывом струи, как изображено на рис. 214. Случай, когда а = я/2, был нами рассмотрен в п. 12.21.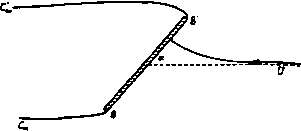

Р и с. 214.

12.30. Отображение относительно свободных линий тока. Мы опишем теперь совершенно иной подход, предложенный Шиффманом ). Этот подход состоит в том, что переменные величины, описывающие течение, продолжаются через свободные линии тока. При этом определяются границы и особые точки области течений. Этот процесс называется принципом отобразкения относительно свободных линий тока. Результат продолжения течения через

гпяосяот

ло-пмосяося

ь-пяосяость

Рис. 215.

свободные линии тока называется образом, или отображением, действительного течения. Будем отмечать звездочками наверху параметры г*, ш*, v* для отображенного течения; соответствующие параметры для действительного течения обозначаются через г, w, v.

Рассмотрим течения с одной свободной линией тока. Для этого обозначим через и величину скорости вдоль свободной линии тока; тогда в плоскости v, или плоскости годографа, свободные линии тока изобразятся дугами окружности

Рассмотрим теперь в плоскостях г, w v линии тока, изображенные на рис. 215; при этом свободные линии тока изображены пунктиром. Не нарушая общности, примем, что ф = О на свободной линии тока.

Так как функции ш и v = -dw/dz являются аналитическими функциями от г, отсюда следует, что переменные г, w, v являются аналитическими функциями относительно друг друга.

Согласно п. 5.53. функцию w можно путем зеркального отражения аналитически продолжить через прямую линию ф = О, на которой она принимает

1) Shi ff man М., Communications on Pure and Applied Mathematics 1 (1948), 89-99, II (1949), 1-11.

действительные значения; поэтому имеем

W* =г W. (2)

Так как в плоскости w линия тока представляется линией, параллельной линии г|з = О, и ее зеркальное отражение относительно ф = О является ее образом, то отсюда следует, что порядок расположения образов будет обратным относительно порядка линий тока (рис. 216).

Далее, в силу формулы (1) величины v и Wlv принимают одинаковые значения на дуге окружности u = t/. Отсюда, согласно принципу аналитического продолжения (см. п. 5.52), ]имеем

и* = - =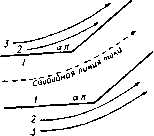

Р I! С. 216.

причем точки v и v являются точками инверсии относительно окружности и = t/.

Поэтому комплексная скорость и ее отображение параллельны друг другу, но модули скорости изменяются в отношении Ulq. Таким образом, приходим к следующей теореме.

Теорема. Отображение элемента линии тока является элементом, измененным по величине, но прежним по направлению. Порядок линий тока при их отображении меняется на обратный.

Пусть dz - элемент линии тока, а dz* - элемент ее отображения. Так

как

и = -

15*=.-=.

dz dz*

TO, используя формулу (2) и учитывая, что на линии тока dw = dw и vdz = = \dz, получаем

V* dz* ~--dw* = - dw = - dw - V dz.

Из этих соотношений и из формулы (3) находим

dz*-dz-dz.

Эта формула дает второе доказательство предыдущей теоремы. Отсюда следует, что длина дуги при отображении меняется в отношении qlU. Рассмотрим несколько частных случаев.

Обтекание угла. Пусть поток обтекает внутреннюю сторону угла ал. При отображении получится поток, обтекающий тот же угол, но

с внешней стороны, как это показано на рис. 216.

В качестве приложения рассмотрим струю, текущую вдоль стенки, состоящей из двух плоскостей, которые образуют угол ABC (рис. 217).

Поток, являющийся отображением, показан на рисунке в виде заштрихованной области. Полный поток, состоящий из действительного потока и его отображения, представляет собой течение в канале, ограниченном стенками ABC и А*В*С*. Линия тока, которая делит пополам канал в бесконечности, есть свободная линия тока, вдоль нее величина скорости постоянна и равна V. Таким образом, А*В* и В*С* являются прямыми, параллельными соответственно прямым АВ к ВС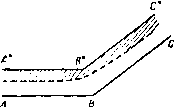

Рис. 217.

И ОТСТОЯЩИМИ от них на расстоянии 2А; причем А - ширина исходной струи в бесконечности; точка В* расположена на биссектрисе угла ABC.

Критическая точка. При отображении потока, обтекающего внутреннюю область прямого угла в окрестности критической точки О, получается поток, обтекающий в г/тре )ю область углаЗя/2; таким образом, отображением потоков, обтекающих прямые углы внутри всей окрестности критической точки, являются потоки на трех листах с точкой ветвления О* (рис. 218).

у

Рис. 218.

Равномерный поток в бесконечности. Пусть поток определяется выражением v = Ve-* , тогда из формулы (3) имеем

,-ia

так что отображением также является равномерный поток. Из формулы (4) получим

Z*= -2 = COnst,

и поэтому г* неограниченно возрастает вместе с возрастанием г. Таким отображением является равномерный в бесконечности поток, параллельный исходному, но скорость его изменена в отношении (/*/V*, равном единице, так как V = и.

Свободные линии тока. Если в потоке есть вторая свободная линия тока, на которой скорость равна V, то формула (4) приводит к уравнению (5), так что отображением является геометрически подобная свободная линия тока. Если V = U, то отображение получается в результате поступательного перемещения исходного потока.

Отображение окрестности произвольной точ-к и. Пусть поток в окрестности точки 2о задается формулой

V = а (г - 2о)Р 4-высшие степени (z -2о), (6)

где показатель степени р - действительное число. Из формул (6) и (4) находим

dz* =

dz+ ....

Отсюда, интегрируя и сохраняя только главный член разложения, получаем

ч2Э+1 , (7)

где Z* - отображение точки Zq.

Комбинируя этот результат с формулой (3), получаем

t3* =

Ч (2р+1)а У

Из формулы (7) мы видим, что если 2р -- 1 > О, то отображением точки Zo является конечная точка; если же 2Р + 1 < О, то отображением точки является точка в бесконечности.

Простой источник. Пусть в формуле (6) а = т - мощность источника и пусть р = -1. Так как А = -т, то отображением является равный по мощности источник в бесконечности, но противоположный по направлению. Обратно, отображением простого источника в бесконечности является равный по мощности источник в конечной точке.

12.31. Насадок Борда. Этот насадок был описан в п. 11.51. В силу симметрии течения достаточно рассмотреть половину течения, как это изображено на рис. 219.

Для простоты рассмотрения верхняя стенка ЛВ дублирована линией Л *С^. Если М - расход, поступающий в насадок, то в бесконечности (в точке В ,)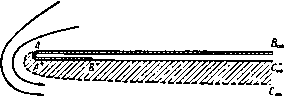

Рис. 219.

имеется источник производительности М. Отображение Л точки Л* совпадает с Л, и поэтому отображением линии Л В является Л *В*, причем в точке В* имеется источник производительности М. Отображением линии В ,Со<, является линия, параллельная B*Qo. Так как скорости в точках Соо и С5, одинаковы и равны по величине скорости на свободной линии тока, то, не производя вычислений, мы видим, что коэффициент сжатия равен 0,5.

Таким образом, мы имеем простую интуитивную картину течения. Из источника в бесконечности жидкость поступает в область между двумя неподвижными стенками ЛВоо и В„Ссо. С ней сталкивается жидкость, вытекающая из равного по мощности источника В, помещенного в точке В*; в результате этого образуется свободная линия тока (или линия постоянного давления) АСас.

12.32. Истечение из отверстия. Эта задача была рассмотрена в п. 11.53. Линия ВооСоо, служащая осью симметрии струи, является линией тока; поэтому достаточно рассмотреть половину течения, показанную на рис. 220.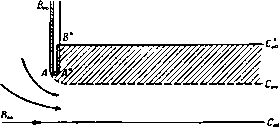

г-плоскост Рис. 220.

Отображением относительно свободной линии тока этой части течения ятляетгя область, пясположенная выше свободной линии тока ЛС ,. огоани-

W- плоскость Рис. 221.

мощностью, как источник в точке Boo, т. е. соответствующей потоку, вытекающему из рассматриваемой половины отверстия. Изображением границы В ,Сос является параллельная ей прямая B*CS>.

Так как скорость течения в бесконечной части струи равна по величине скорости на свободной линии тока, то толщина струи в бесконечности сохраняется при отображении. Таким образом, не производя вычислений, мы видим, что коэффициент сжатия струи превосходит 0,5. Следовательно, интуитивно течение можно рассматривать как течение жидкости между стенками Вес А В* С* и ВосСас, свободная линия тока образуется при столкновении потоков, вытекающих из источника в бесконечно удаленной точке Boo и из равного по мощности источника в точ- -7 о I ке В*.

р . а~а 2 Положение отображенной точ-

ки В* не является произвольным.

е.-плоскость

Оно полностью определяется усло-Р и с. 222. вием симметрии в плоскости w

(рис. 221); в этой плоскости линия В^Со является зеркальным отражением линии ВооСоо относительно действительной оси ф = 0; при этом точка А соответствует точке отрыва потока.

Попытаемся теперь получить аналитические выражения для рассматриваемого течения. Отобразим область течения на верхнюю полуплоскость S, как показано на рис. 222.

Преобразование Шварца - Кристоффеля дает

dw -KZ, dz Ц

здесь К тл L - константы, подлежащие определению. Отсюда путем деления находим

> 1/2

dw К f С-1 \t

и поэтому К=Ш, так как v-U при оо.

Сделав в предыдущих формулах подстановку С =-cos X и выполнив интегрирование, получим

w= -K\ns\nX + M,

z = /L(tg--Я) + Л/,

V = iU ctg ~,

здесь М и - константы.

ченная ею и изображениями линий ЛВ и ВсоС<х>. Отображением точки отрыва А является совпадающая с ней точка А*\ поэтому отображением линии АВо служит конечный прямолинейный отрезок А*В*, совпадающий по направлению с линией ЛВоо. При этом в точке В* помещается источник с такой же