примеры 295

Введем в формулу (7) это выражение, а также подставим значение 2о(в) из формулы (3). Тогда для свободной линии тока касательного решения получим уравнение

z,= {e-t-,sin0 + t [Xcose + y(l-X )]]-, (11)

где Х = 1 -l-lnctg-i-e.

Если 6 = Y я, то мы имеем Я, = 1 и

Ч1)=т(т+0=Ч1+0-

В бесконечности 6 = 0, Х=со; учитывая, что Я,sin6->О, получаем zi(0)=y-{t (-00)} = -£00.

Мы легко можем показать, что давление на свободной линии тока постоянно. Действительно, из формулы (11) следует

2gyi=U*{2kcosB+l-X*). (12)

Кроме того, из формулы (4) п. 11.63 имеем

Следовательно,

= -г'(Р)2(Р).

Таким образом,

dz- к ctge

Складывая это равенство с равенством (12), получаем

q + 2gyi = 2U\

Согласно теореме Бернулли, это уравнение показывает, что давление на поверхности струи постоянно.

ПРИМЕРЫ К ГЛАВЕ 11

1. Несжимаемая невесомая идеальная жидкость занимает всю плоскость, кроме следующей границы:

- а<У<+а, 0< <oo.

Жидкость втекает в точке х = 0 и вытекает в точке х=оо. Показать, что, после того как достигнуто установившееся состояние, асимптотами свободных линий тока будут линии у = ± 0/2.

2. Рассмотрим течение, изображенное на рис. 201; если ширина отверстия равна я-Ь2, то доказать, что скорость q на центральной линии струи на расстоянии Л от отверстия определяется из формулы

q U-q

3. Показать, что в случае насадка Борда (см. п. 11.51) справедливо равенство

x = 2aasin -ie-lnsec-i:e / я;

нарисовать свободные линии тока.

4. Жидкость течет в отрицательном направлении оси у между двумя плоскостями: -**±в. У>Ь- Жидкость встречает барьер, определяемый уравнением у=0, />д:>-/.

Скорость для больших положительных значений у равна V. Определить наибольшую скорость двух струй и результирующее давление на барьер.

5. Плоская безвихревая струя несжимаемой жидкости вытекает из воронкообразного отверстия, стенки которого образуют угол 2а, причем ширина отверстия на выходе равна 2с. После выхода струя ограничивается ссвободными линиями тока* i)=±p, причем скорость вдоль каждой из иих равна V.

Доказать, что движение определяется следующими уравнениями:

2а du

dz р

ли 1а

1+ \

пи 2а

slnudu

Найти в этом случае коэффициент максимального сжатия струи и показать, что он равен л/{л--2), если а=л/2.

е. Показать, что преобразования

ю=у41п 1)-Ь0, /=ch {(а-С)/В)}

(где а=1п(-dz/dai), величины А, В, С, D являются постоянными, значения которых надо найти) дают двумерное струйное течение жидкости, вытекающей из отверстия шириной 2а в плоской стенке.

Доказать, что предельная ширина струи равна 2яа/(я--2) и что уравнение одной из ее границ может быть представлено в виде

2а

(lntg--bcose).

2а

(l-sinO),

если за начало координат взять край отверстия. Здесь в -угол наклона границы струи к вектору скорости иа бесконечности.

7. Жидкость вытекает из отверстия, расположенного в середине дна сосуда с вертикальными стенками бесконечной высоты. Будем считать движение двумерным и пренебрежем действием силы тяжести. Считая, что область в плоскости г, занимаемая жидкостью, ограничена указанным выше образом, изобразить соответствующие области в плоскостях о; и Q, где Q=\n(-dz/dw).

Получить уравнения вида

согласно которым каждую из указанных областей можно было бы конформно отобразить на верхнюю полуплоскость плоскости вспомогательного переменного t. Показать, как можно определить все константы, встречающиеся в выражениях функций fi(/) и /2(0-

(Граница области z состоит из следующих частей: (1) полубесконечная линия х=0, у>0; (2) отрезок у=0, a>x>0; (3) свободная линия тока, выходящая из точки z=a и имеющая асимптоту х=Ь, которую требуется определить; (4) бесконечная линия х=с, где с>Ь>а.)

8. Исследовать движение, задаваемое конформными отображениями вида

dQ 1 У{Ь-а)(Ь-а')

2 (t-b)Y{t-a)(t-a) V(b-a) (t-T) + y (йИЙГГР) /(a-a) -6)

Вычислить ширину сосуда, выразив ее через окончательную ширину струи, при которой скорость равна Q; определить также уравиеиия кривых, ограничивающих струю я ее окончательное направление.

Показать, что в случае, когда п=1, 6=0 и а=оо или а'=-аэ, мы получим струю Гельмгольца с профилем в виде трактрисы (линия погони). Описать любой другой простой случай, например соответствующий зиачеиням а=оо, а'=0.

примеры 297

9. Неподвижные границы жидкости, движущейся в плоскости (х, у), заданы уравнениями

у=х - а (у<:-а), у=-х+а (у>а).

Полуплоскость, содержащая отрицательную часть оси х, полностью заполнена жидкостью, покоящейся в бесконечности и вытекающей из отверстия между точками (О, а> и (О, -о). Показать, что предельная ширина струи иа бесконечности равна

In (/2-0-1-/2+-= Определить вид свободных линий тока.

10. Двумерная струя жидкости вытекает симметрично из области, ограниченной двумя плоскими стенками, наклоненными друг к другу под углом 2а. Концы стенок находятся на равных расстояниях от точки пересечения. Показать, что конформное преобразование, приводящее к решению задачи, определяется формулами

2а

.= ?*e-ia(<+/(iiZrr)) ,

dt nt

dw 2bV dt ~ nt

где 26 -предельная ширина, a V-предельная скорость струи на бесконечности. Доказать, что если 2с-ширина отверстия между стенками, то

=b[i+- Jtgesin{a(i-)}de].

11. Поток, ширииа и скорость которого в бесконечности соответственно равны ег и V, течет по стороне у>0 препятствия, задаваемого формулами

j,=0, -cx)<x<0, x = 0, 0<j,<a.

Показать, что двумерное безвихревое движение жидкости при отсутствии массовых сил задается уравнениями вида

dw А dQ В f у

dt -(t-\)(t-X) dt-yjfilTi) - V dwj

где - 1<Х<-(-1. Найти величины А и В и затем найти уравнение для определения угла а, на который поток отклоняется.

12. Насадок Борда шириной а симметрично установлен в основании широкого прямоугольного сосуда шириной ка и простирается внутрь на большое расстояние от основания. Доказать, что внутри сосуда на некотором расстоянии от насадка течение практически представляет собой параллельный поток. Доказать также, что коэффициент сжатия равен k-(k-kf. Получить результат п. 11.51 в качестве предельного случая.

13. Если на рис. 203 точки D, D соответствуют значениям J = -о, t, = a (а<1), то показать, что

dO --- --

- = 2(S2-a2) 2(S-1)

Изобразить общий вид соответствующей диаграммы в плоскости U/v. Если U=vre на участке диаграммы, соответствующем линиям BD, BD, то показать, что

lnr=lnro-[-ectga,

где величина Гд равна г при В = 0.

14. Показать, что в п. 11.54 вдоль линии BD справедливы равенства

и, следовательно.

26 г

s=--dl.

rcosef. ,= -f rsinef .

где

16. Показать, что если положить а=я/4 в условиях п. 11.54, то имеют место равенства

Q = 2 \ £ ,1 0 = 1/2

Вычислить координаты (х, у) для значений а=0,2; 0,4; 0,6; 0,8 и, таким образом, изобразить внд насадка.

16. Выяснить применимость метода, приведенного в п. 11.54, для нахождения потока через отверстие, в котором края соответствующим образом закруглены.

Вывести формулы

Глава 12 ДВИЖЕНИЕ ПО СХЕМЕ ГЕЛЬМГОЛЬЦА

12.10. Кавитация. Рассмотрим цилиндр, полностью погруженный в несжимаемую жидкость, покоящуюся на бесконечности, например в воду, и движущийся справа налево со скоростью U. На рис. 206, (/) показана начальная стадия движения цилиндра (см. также фото 1), когда скорость движения невелика и вся поверхность цилиндра смочена жидкостью. В этом случае точки минимального давления находятся на концах диаметра, перпендикулярного направлению движения.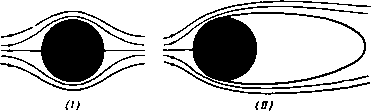

Рис. 206.

На рис. 206, ( ) показано движение цилиндра с достаточно большой скоростью'). В этом случае было обнаружено, что жидкость отделяется от поверхности цилиндра в его кормовой части. Происходит образование пузырей, или каверн, ограниченных свободными линиями тока и заполненных парами жидкости.

Пусть П - давление жидкости в бесконечности, - давление пара в каверне. Тогда, следуя Прандтлю, определим число кавитации а следующим образом:

П-Ре У*-и* ~ 42QU* ~~ и* где второе равенство получено путем использования теоремы Бернулли, причем V - скорость жидкости на границе каверны.

В случае двумерного движения установлено, что ширина каверны имеет порядок a, а ее длина - порядок а'*. Таким образом, и ширина и длина каверны увеличиваются вместе с уменьшением величины о. Пусть атмосферное давление поддерживается постоянным и скорость течения воды достаточно велика. В этом случае для каверны в воде величина о будет положительной, так как давление водяного пара меньше атмосферного давления. Если скорость и увеличивается, то из формулы (1) следует, что число а убывает и поэтому о ->- О, когда и со; при этом соответственно неограниченно возрастают ширина и длина каверны.

В настоящей главе мы будем рассматривать главным образом так называемое плоское течение Гельмгольца, который впервые изучил это течение. Данное движение характеризуется следующими свойствами:

*) Точнее, с достаточно большим числом Рейиольдса (см. п. 19.62).

p-TQq = const;

(3) давление в каверне равно давлению в невозмущенном потоке, т. е. Рс = П, и поэтому число кавитации равно нулю.

Что касается свойства (1), то различие между течением без учета силы тяжести (например, течение жидкости в свободно падающем баке) и течением с учетом силы тяжести будет незначительным, если объект, вызывающий кавитацию, движется горизонтально и с большой скоростью. Результат действия силы тяжести существенно зависит от числа Фруда, определяемого выражением

g.(Длина каверны)

которое стремится к нулю при о 0. В этом случае эффект силы тяжести незначителен.

Так как рассматриваемое течение установившееся [свойство (2)], то можно считать, что тело остается неподвижным, а жидкость обтекает это тело.

12.12. Правильная кавитация. Правильной кавитацией называют такое разрывное течение жидкости, при котором минимум давления достигается на свободных линиях тока. При неправильной кавитации минимум давления имеет место на поверхности препятствия.

Различие между правильной и неправильной кавитацией представляет интерес в силу следующих свойств установившегося течения.

(1) При правильной кавитации свободные линии тока обращены выпуклостью в сторону жидкости.

Доказательство. Градиент давления вдоль нормали, проведенной к линии тока внутрь жидкости, будет положительным. Поэтому ускорение частицы, нормальное к ее траектории (к линии тока), будет направлено внутрь каверны. Следовательно, граница каверны будет выпуклой в сторону жидкости.

Аналогично доказывается (без учета силы тяжести), что скорость достигает минимума в точке, где граница обращена выпусклостью в сторону жидкости.

Следствие. В случае прямолинейных препятствий правильная кавитация не отличается от неправильной.

(2) Скорость течения равна нулю или бесконечности в тех точках линии тока, при подходе к которым с разных сторон направление скорости стремится к разным пределам.

Следствие. В точках отрыва от препятствия линия тока имеет непрерывную касательную.

(3) Пусть в точке Р линия тока разделяется на две ветви Я, и Яг, так что касательная в точке Р непрерывна, а кривизна в этой точке зависит от того вдоль какой ветви ki или к^ следует приближаться к точке Р. В этом случае скорость не может быть постоянной на линиях Ki и Xj.

Доказательство. (Сохраняя обозначения п. 12.43, будем рассматривать бит как функции комплексного потенциала w на линии, например, ф = 0. Кривизна выражается следующей формулой:

dO dB dw i/gx dQ

dk ~ dw di. dw

Функция e непрерывна вблизи дуги кривой, на которой скорость постоянна по величине, поэтому разрыв производной dQIdX влечет необходимость разрыва множителя dQ/dw. Следовательно, производная dx/dw имеет

(1) течение жидкости происходит без учета силы тяжести;

(2) течение установившееся, т. е. справедливо равенство

логарифмическую особенность. Поэтому величина т не может оставаться постоянной на линии тока в двухсторонней окрестности точки разрыва ее кривизны.

Следствие (I). В точке отрыва от препятствия кривизна линии тока или непрерывна, или обращается в бесконечность.

Следствие (И). В случае правильной кавитации кривизна линии тока будет непрерывной в точке отрыва от препятствия, ограниченного линией конечной кривизны; действительно, согласно свойству (1), линия тока не может быть вогнутой, а выпуклая линия тока с бесконечной кривизной должна была бы пересечь препятствие.

12.20. Прямой удар струи о пластинку. Предположим, что струя конечной ширины, имеющая скорость U, встречает неподвижную пластинку ВВ шириной I, расположенную под прямым углом к потоку, как изображено на

Z плоскость

плоскость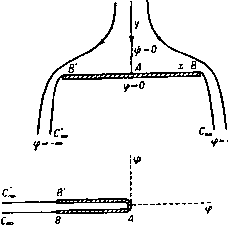

1-плоскость

и/и пяоскоста

Q-плоскость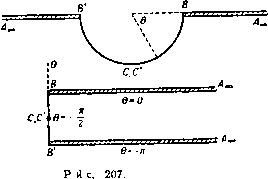

рис. 207. Точку А в середине пластинки примем за начало координат, а ось х направим по линии АВ. Линия тока, попадающая на пластинку в точке Л, рааветвляется на две линии, которые идут по пластинке к точкам В и В' и затем переходят в свободные линии тока ВС и В'С'оо- Область вакуума между свободными линиями тока является каверной.

Q = Arch(-)-1я. - j = ch{in + Q)= -chQ. Q = Arch=ln(i-f/1-1).

Предположим, что разветвляющаяся линия тока соответствует значению >) = 0 и что ф=0 в точке А. Тогда в точках С , и С имеем ф = - оо. Плоскость w изображена на рис. 207, где для ясности части границы С'тВА и СооВА расположены на некотором расстоянии друг от друга, хотя в действительности они совпадают с отрицательным направлением оси ф.

Диаграмму в плоскости ш следует рассматривать как многоугольник, у которого границей является С'а>В АВСсо, внутренняя область совпадает со всей плоскостью ш, внутренний угол в точке А равен 2я. С помощью преобразования Шварца -Кристоффеля отобразим такой многоугольник на верхнюю половину плоскости так, чтобы точки В\ А, В соответственно переходили в точки 1, О, 1. Это преобразование определяется фор-

= КС, w=\kI\ (1)

так как ш = 0 при С = 0-

Рассмотрим теперь соотношение

-Udzldw=Ulv.

Представим это соотношение на векторной диаграмме; считая, что z описывает линию АВСооС ,В'А, на плоскости U/v мы получим фигуру, показывающую, что argi - Udzldw) уменьшается на я, когда мы идем от точки А вдоль линии АВС„С'соВ'А. Поэтому плоскость Q имеет вид, изображенный на рис. 207 (см. также рис. 202).

Полуполосу плоскости Q отобразим на верхнюю половину плоскости I, при этом точки В', В, Лоо, которые являются вершинами внутренних углов, равных соответственно УзП, Ч^п, О, должны перейти в точки 5=-1, 1, 0. Для такого отображения по формуле Шварца - Кристоффеля имеем

dQ К'

Q = -/KArch(-)+Z-.

Далее, если ;=-1, то Q=-in; если S = l, то Q=0. Поэтому имеем

L=-in, -iKiin) + L = 0,

и, следовательно. Отсюда получаем Поэтому Но

Таким образом, находим

D = (p-n)dx = ±Q\{U*-q*)dx,

где интеграл вычисляется по пластинке от точки В' до точки В. Так как отрезок АВ совпадает с осью х, то, следовательно,

Поэтому

Применив формулы (1) и (3) из п. 12.20, получим для последнего интеграла следующее выражение:

Таким образом, имеем

Эта формула дает лобовое сопротивление (отнесенное к единице толщины потока).

Выбор знака перед корнем производился из условия, что в точке А при С = О имеется критическая точка, так что производная dw/dz должна обращаться в нуль при =0. Но при малых значениях J квадратный корень в формуле (2) очень мало отличается от 1/, так что dw/dz->О при С -* О-

Далее, из формулы (1) следует, что dw/di = Kt. Поэтому

l = l([-l yjr:i)], (3)

Интегрируя это соотношение от точки В' до В, т. е. от $ = - 1 до S= мы получим

1 я/2

Ul=-к \[\+VlJ)]dt=~f( \ (H-cos9)cosede=-/c(2+in).

-1 -я/2

Определив из этого соотношения величину К и подставив ее в (1), мы получим формулу

-15- (>

Таким образом, решение задачи выражается формулами (2) и (5).

12.21. Лобовое сопротивление пластинки. В случае прямого удара струи о пластинку полное давление на пластинку, или лобовое сопротивление, определяется путем применения теоремы Бернулли

где р и </-давление и скорость на обтекаемой стороне пластинки; П - давление в каверне.

Отсюда лобовое сопротивление D выражается формулой

12.22. Коэффициент лобового сопротивления. В экспериментальных работах принято выражать лобовое сопротивление посредством коэффициента лобового сопротивления Со, определяемого равенством

D = Cd~qUS,

где S - площадь проекции обтекаемого тела на плоскость, перпендикулярную к потоку. В только что рассмотренном случае обтекания пластинки, перпендикулярной к потоку, коэффициент лобового сопротивления равен

Эта величина коэффициента согласуется с экспериментальными значениями для движений с хорошо развитой кавитацией.

12.23. Задача Рябушииского. Пусть в равномерный поток скорости U помещены две (вместо одной) параллельные пластинки. При этом концы пластинок соединены свободными линиями тока (рис. 208). Полученная схема течения впервые была исследована Рябушинским^).

В этой схеме пластинки расположены перпендикулярно направлению невозмущенного потока, которое совпадает с линией, соединяющей середины пластинок. Здесь точка М обозначает середину свободной линии тока, соединяющей концы пластинок. Поток имеет две оси симметрии, с которыми совмещены координатные оси Ох и Оу. Комплексная скоростыз имеет значения V, tV, О, U соответственно в точках М, А, В, Соо, где V-постоянная величина скорости на свободной линии тока.

На рис. 209 изображена четвертая часть потока иа плоскости v/V (плоскость годографа), а также на плоскости v*/V*. На первой плоскости свободная линия тока переходит в дугу четверти окружности, так как иа ней \v\ = V. На второй плоскости свободная линия тока переходит в дугу полуокружности. Эту полуокружность отобразим на верхнюю половину плоскости С, изображенной на рис. 210, с помощью преобразования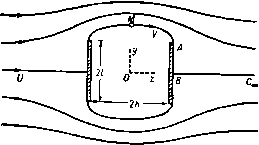

Рис. 208.

Рис. 209.

В С М iyV-пдоскоппо

которое переводит точку А в точку С = 1 и точку М-в точку С = - 1 Для определения отображения на плоскости w можно положить в силу симметрии <р = 0 на оси у, а также ф=0 на свободной линии тока. Рассматриваемая здесь часть потока отображается на третий квадрант плоскости w и, следо-аательно, на верхнюю половину плоскости ш* (рис. 211).

С помощью преобразования Мебиуса (см. пример 14, гл. 5)

= $f. a6-PY¥=0, (2)

1) Riabouchinsky. Proc. Lnd. Math. Soc. (2), 1 (1921), 206-215.