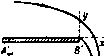Подставляя это соотношение в формулы замечания (П1) и учитывая, что обе оордннаты хну обращаются в нуль при 6 = 0, находим следующие выражения:

x=f-cosetg--de, y = lsmetg-dQ.

После интегрирования получаем

x = °(sin -lnsec). z/ = (e-sine).

Эти уравнения позволяют начертить линию тока 5С ,. Теперь в точке Сое имеем 6= я и, следовательно, у = оа. Таким образом, согласно рис. 200, на плоскости z имеем

2а = 2оа--оа--аа, откуда о = /а. Этот результат был получен Борда.

11.53. Истечение через отверстие. Рассмотрим жидкость, вытекающую из большого сосуда через отверстие в одной нз его стенок. Жидкость будет вытекать в виде струи, ограниченной свободными линиями тока, вдоль которых скорость постоянна, а в бесконечности течение в струе будет равномерным, т. е. скорости течения будут одинаковы по величине и направлению.

На рис. 201 показано такое движение.

Если в точках В и В' положить ф = О, то будем иметь ф = - аэ в точке Сое и ф= -(-оо в точке Есо, где центральная (прямая) линия тока, на которой ф = 0.

Пусть ВВ = 2а и пусть U - постоянная скорость в точке Соо. Тогда расход в струе в сечении СовС равняется 2aaU, где о - коэффициент сжатия струи. Следовательно, линия j4ooiBCoe является линией тока, соответствующей ф= -oaU, а линия А'ааВ'С' является линией тока для ф= oai/.

Таким образом, область течения в плоскости W будет такой, как изображено на рис. 200; после отображения на плоскость С этой области получим

w=\n-iaaU. (1)

Однако диаграмма в плоскости U/v будет отличаться.

Когда точка z движется вдоль границы ВСсоС'огВ', то мы получаем диаграмму, изображенную на рис. 202. Когда мы идем от точки В' к точке В, то arg (U/v) уменьшается на я, так что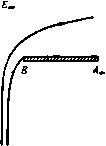

2 плоскость Ри . 201.

U/v-oMKnocmt

В

Qneocnoant

Р и с. 202.

р=/в(о>е>-1я)

Р=/в(-1я>0>-я)

dQ- я

Используя замечание (III) п. 11.52, получаем

в

x = cos 0 tg 0 dO = (1 - cos 0).

в точке С'оа имеем 0= -уя, х=2аа/п; здесь величина х является горизонтальным расстояниам между точками В' и С' . Следовательно,

2а^2аа+-, 0= = 0,611.

11.54. Криволинейные границы. Метод решения задачи Борда в п. 11.51 показывает, что успех решения зависит исключительно от того, что диаграммы течения в плоскостях ш и Q ограничены пряными линиями. Это дает возможность применить теорему Шварца - Кристоффеля.

D С.С D

ВГ-в , в'

те-

р

Рис. 203. Рис. 204.

Как было установлено Шильдропом, решение, соответствующее закруглению насадка Борда у входа вточках ВВ, можно получить путем незначительного изменения диаграммы в плоскости Q, остающейся все еще многоугольником (рис. 200).

в самом деле, заменим диаграмму в плоскости Q диаграммой, изображенной иа рис. 203 и полученной путем скругления углов диаграммы рис. 200-прямыми линиями, наклоненными под углом а к параллельным прямым. Теперь, возвращаясь к плоскости г с помощью обратного преобразования, мы получим насадок с закругленным входж, изображенный иа рис. 204.

После отображения плоскости Q на плоскость согласно п. 10.31 (при этом начало координат передвинуто в точку Q= -in), мы получим

Q=Arch5-ш. (2)

Формулы (1) и (2) дают решение рассматриваемой задачи.

Для определения коэффициента сжатия струи используем общий метод п. 11.52. Возьмем начало координат в точке В' и рассмотрим свободную линию тока В'С'оа, на которой величина £ действительна и увеличивается от -1 до 0. Тогда из формулы (1) п. 11.52 получаем

1 яС ds

*---Щ-!

так как теперь производная ds/d положительна, в то время как величина £ отрицательна.

С другой стороны, на линии В'С^ имеем Q-iQ, и, следовательно, из формулы (2) находим

/0= Arch;-/я, С=-cosO, dC = slnede.

Таким образом,

ds 2аа . = -tgO.

Практические расчеты обычно проводятся с помощью графических или приближенных методов. Интересно отметить, что такое простое видоизменение диаграммы позволяет получить решение для насадка, близкого к реальному. Этот метод применим ко всем задачам, которые имеют в плоскостях Q и W диаграммы в виде многоугольников. С подробностями читатель может ознакомиться по оригинальной статье).

11.60. Поток со свободной поверхностью под действием силы тяжести.

Своободная поверхность является поверхностью, которая всегда состоит из одних и тех же частиц жидкости и вдоль которой давление жидкости постоянно.

В случае двумерного движения такая свободная поверхность является цилиндрической; мы будем рассматривать кривую, представляющую собой сечение этого цилиндра плоскостью движения жидкости.

Пусть кривая С является сечением свободной поверхности. Вид кривой С зависит от времени /, параметрически эту линию можно представить в виде

z=f(a, t) на линии С, (1)

где а -действительное значение координаты Лагранжа (см. п. 3.44) для частицы жидкости на кривой С, так что полная производная по времени от z совпадает с частной производной по времени от /, т. е.

Если g - ускорение силы тяжести, то уравнение движения можно представить в виде

dq/d/-g=-(Vp)/e. (3)

Поскольку вектор Vp перпендикулярен поверхности постоянного давления, то условие постоянства давления на свободной поверхности состоит в том, чтобы вектор dq/d/ -g был перпендикулярен свободной поверхности*).

В случае двумерного движения жидкости это условие равносильно тому, что вектор dz/dt + ig перпендикулярен кривой С, когда конец вектора z находится на кривой С. Так как fa имеет направление касательной к кривой С, то из формул (2) мы видим, что на линии С имеет место уравнение

ftt + ig=ir{a, t)fa, (4)

где г (а, /) -действительная величина, если а- действительная. Таким образом, самый общий вид двумерной свободной поверхности может быть представлен формулой (1), где функция /(а, /) для действительных значений а есть решение уравнения (4), которое является дифференциальным уравнением в частных производных параболического типа.

Заметим, что сомножитель /г (а, t) указывает направление уменьшения давления.

Определение соответствующего вида функции г (а, t) составляет основную трудность общей задачи (ср. п. 11.63).

Если функция г {а, t) задана, то задача сводится к решению уравнения (4) при определенных граничных условиях. Заметим также, что если функция г {а, t) задана, то уравнение (4) является линейным уравнением OTHOCHTCvibHO / (а, /). Следовательно, решение можно получить с помощью принципа суперпозиции.

1) S с h i е 1 d г о р Е. В., Skrifter Oslo, № 6, 1928.

) Это условие может быть положено в основу при решении трехмерной задачи.

11.61. Потенциальный поток со свободной поверхностью. Обращаясь к формулам (1), (4) п. 11.60, определим ксшплексиый потенциал w(z, t), предполагая, что движение жидкости безвихревое.

Мы имеем u + iv= поэтому

Отсюда и из формулы (2) п. 11.60 получим

ft (о, t) = -Wt{z, t) на кривой С. (2)

Используя формулу (1) п. 11.60, мы можем выразить w{z, t) в виде функции от а и поэтому на кривой С получим

Wa (а, /) = ю, (2, t) 2 - - МоГО и (а. i)

Так как величина а действительна иа С, то это соотношение можно записать в форме

Wa (а, о = -ГЖ1) fa (а, t). (3)

Если предположить, что /(а, /) и ft (а, /)-аналитические функции от а, то правая часть равенства (3) также является аналитической функцией от а. Таким образом, мы можем использовать формулу (3) для определения комплексного потенциала w как аналитической функции комплексного переменного а и, следовательно, аналитической функции комплексной переменной 2. Определенный таким образом комплексный потенциал w (г, t) является комплексным потенциалом потока, который имеет свободную поверхность, совпадающую со свободной поверхностью, задаваемой уравнением 2 = / (о, /).

Следовательно, всякое аналитическое решение f(a, t) уравнения (4) п. 11.60, где коэффициент г (а, t) является действительной функцией для действительных значений а, описывает возможное движение жвдкости со свободной поверхностью, для которого соответствующая свободная поверхность имеет вид z=f{a, f), а комплексный потенциал определяется из формулы (3) с помощью квадратуры*).

11.62. Установившийся поток со свободной поверхностью. Зафиксируем оси Хо, Уо- Пусть Zo=Xo+iyo, пусть комплексный потенциал Wo=Wo (zo)=Фо-- 1о-Пусть свободная поверхность является линией тока фо = О, так что иа свободной поверхности

Фо=0. ao(2o)=ao(2o). (1)

Следовательно, на свободной поверхности мы инеем

, dwp dwp Фро йфо /п\

-dZ-dWo

Учитывая, что давление постоянно на свободной поверхности, по теореме Бернулли получаем

1 dvsdsa, Q. = 1V , (3)

где Qo-потенциал силы тяжести. У-постоянная, имеющая размерность скорости. Подбирая подходящим образом начало отсчета, мы можем всегда

1) Описавши здесь метод см. в работе: John F., Commttnications on Pun and Applied Mathematics, VI (1963), 497-f

добиться того, чтобы постоянная V* была положительна. Из уравнения (3) находим

dzp dzp 1 свободной поверхности. (4)

do V -2Qo

Пусть компонентами силы тяжести являются (gsina, - gcosa). Тогда Qo=-1/(206-* -V), (5)

это выражение равно gyo, когда а = 0, и равно -gx, когда а = --я.

Пусть а обозначает фиксированную (характерную) длину, введем безразмерные величины z, W, Q, F*, определяемые формулами

2о=а2, Wo = aVw(z), Qo = agQ, F*=V*/{ag). (6)

Тогда уравнение (4) можно записать в виде

j- = f 20( p) Д свободной поверхности. (7)

Здесь 7=-число Фруда (ср. п. 12.10), которое обращается в бесконечность прн = 0. Уравнение (5) при этом приводится к виду

Й=-1-1(26-* -zi ). (8)

Дифференцируя его по ф, получаем

е* = - 2/ иа свободной поверхности. (9)

В связи с этим замечаем, что на свободной поверхности величины z и 2 связаны функциональной зависимостью и, следовательно, величина Q, определяемая формулой (8), есть функция от ф, т. е.

Q=Q((f) на свободной поверхности. (10)

Далее, исключая dz/d<f нз формул (7) и (9), получим

W(w*°-2) = fi Л поверхности. (11)

Это уравнение определяет z как аналитическую функцию от ф. Следовательно, поскольку ш=ф на свободной поверхности, где удовлетворяется соотношение (11), то мы имеем уравнение

dz dw

Это уравнение определяет z как функции от ш и содержит произвольную аналитическую функцию Q(a ), которая принимает действительное значение С(ф) при ф = 0.

Заметим, что функция П(ф) вначале не известна, так как она может быть определена нз соотношения (8) только в^ том случае, если определено функциональное соотношение между 2 и 2.

Если мы зададим вид функции 0(ф) или Q{w), то мы сможем найти соответствующий поток. Это соображение принадлежит М. Сотро*).

Sautreaux М. С. , tSur une question dhydrodynamique*, Ann. Scient. de

I Eooie, Sup6rieure, 10 (1893), 95-182.

x+iy = z=ia{w)±\ /(-Q*(w)-£yw. (17)

Если в формуле (17) положить ф=0, то получим уравнение линии тока ф = 0, при этом хну выражаются в зависимости от параметра ф. Для тех значений ф, при которых подкоренное выражение отрицательно, мы получим х = const, так что часть линии тока ф=0 будет состоять из вертикальной линии, которую можно заменить твердой стенкой или границей. Следовательно, свободная линия тока будет соответствовать тому случаю, когда подкоренное выражение положительно. Учитывая также уравнение (7), в котором выражение, стоящее в левой части, обязательно положительно, мы увидим, что иа свободной линии тока выполняется условие

. <М=£!<о. (18)

Таким образом, это неравенство ограничивает область значений ф, соответствующих точкам иа свободной линии тока. Пример I. Имеем

Я = 1, 2Q(a )-l = 2oy, а=0. Тогда из формулы (17) находим

x + iy = z = i(w+\)± \ (19)

Линия тока ф = 0 определяется из уравиеиия

х + -4, = .(ф + у)-$ ]/(-1-)Ф. (20)

где для корня мы выбрали отрицательный знак.

Если обозначить штрихами дифференцирование по w, то уравнение (12) может быть записано в виде уравнения

2 -2fQW-f-2 = 0. (13)

которое также равносильно соотношению (И) на свободной поверхности.

При а=0, т. е. в том случае, когда ось у направлена вертикально вверх, имеем

/ -2.W + 2Q?=0. (14)

Если £ = 0, то величина F* равна бесконечности и уравнение (14) принимает вид

2 -2<Qz-l = 0. (15)

Следовательно, это уравнение может быть использовано для определения всех потоков со свободными линиями тока, если гравитационное поле отсутствует.

Решая уравнение (14) относительно z, получаем

= /О'И ± /( о'.(ш)-2(згО 06)

Так как dz/dw= - l/(u - iv)= -u/q* - iv/q\ то мы найдем величины и н V как действительную и мнимую части выражения, стоящего в правой части формулы (16).

Интегрируя выражение, стоящее в формуле (16), находим

Подкоренное выражение имеет отрицательный знак для значений ф, лежащих в интервале ( -Va, 0). Для значений ф вне этого интервала имеем * = const. Таким образом, линия ур = 0 частично состоит из вертикальной стенки. Если - 7 <ф<0, то, полагая ф= - V4(l--cos20), получаем

x-b/i/=t(l-cos2e)- J sin ede=-t(l-cos2e)-4в + :-sin2e-l-C. (21)

Здесь постоянная С произвольна, однако будет удобно (но не обязательно) придать ей значение /4 . Тогда мы получим

х = 1 я-у 0-1-4 sin 26, / = 1(1-cos 26).

(22)

Это уравнение является уравнением циклоиды, точками возврата которой являются точки 6=0, (Vi . 0). Э = я, -0 а вершина циклоиды

находится в точке 0=-2 я, (О, Vj).

Из уравнения (16) при \) = 0 имеем

Таким образом, о = 9* tg 6, v = -q*. Если 6 = уЯ, то u/q* = со и, следовательно, и= 0 = = 0. Это означает, что вершиной циклоиды является критическая точка. Когда величина 6 изменяется ot */аЯ до О, то величина и положительна, в то время как при изменении величины 6 от я/2 до О, величина U-отрицательна. Таким образом, циклоида описывается в противоположном направлении, когда частица движется от

вершины к точкам возврата; фактически поток симметричен относительно вертикали * = 0.

Следовательно, используя эту симметрию, мы получаем поток, изображенный на рнс. 205.

Для внутренних линий тока имеет место соотношение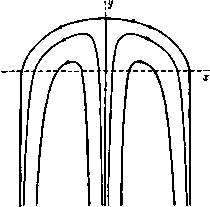

Рис. 205.

oy=-:j-fl+cos(20-l-2iTi)I,

которое сводится к равенству ф=-1 (I + cos26), когда т| = 0. Из формулы (23) получаем равенство

ф = 1з1п205Ь2л, (24)

котооое определяет линии тока ф= const. В частности, ф = О либо при

ц = 0 (только что рассмотренный случай), либо при 6 = 0, V ff, я.....

Таким образом, поток является периодическим повторением потока, изображенного на рис. 205. Пример II. Имеем

Я = оо, Q(z ) = e . а=-уя.

В этом случае сила тяжести отсутствует; таким образом, мы получаем поток через отверстие, который был рассмотрен в п. 11.53.

(23)

=е + 1/(е2Ф-1), (26)

где взято положительное значение корня.

Если ф > О, то выражение, стоящее в правой части, действительно, и так как -d(f/d2 = u - iv, то v = 0. Это означает, что имеется твердая стенка, параллельная оси х, с которой при подходящем выборе начала координат она будет совпадать.

При ф < О положим

e =sin0, (27)

тогда уравнение (26) принимает вид

= ctg 6 (sin 6 + i cosO) = cos 6 -f- / - sin 0 . В результате интегрирования получим

2 = -i-n + sin0 + i (cosO + lntglo) , (28)

где произвольная постоянная взята равной Vj. Отсюда находим свободную линию тока в виде

Х = уЯ + 81пв, l/=COSe + lntge.

Если в уравнении (25) мы напишем 1з = л вместо ф=0, то получим в гору ю свободную линию тока, для которой формула (27) приводится к виду в =-sin0. Для получения уравнения мы просто изменим знак

у величины 0 в формуле (28). Так как 1п - tg-jO =1я--1п tg-1-0, то

для второй свободной линии тока мы получаем следукицую формулу:

г= lfl-sin0-f-<(cose-blntg-ie) .

Вторая свободная линия тока является зеркальным отражением линии, определяемой формулой (27), относительно оси у.

Построенный поток изображен на рис. 201, но здесь начало координат расположено посредине между точками В и В'.

Ширина отверстия в наших безразмерных координатах равна

2(*/2Я--8Шя/2), а ширина струи в бесконечности равна 2 (я/2--sin 0). Следовательно, коэффищ|ент сжатия равен я/(л-Ь2).

11.63. Касательные потоки. Пусть в формуле (1) п. 11.60 точка Zo обозначает точку свободной поверхности. При этом предполагается, что движение установившееся. Определим лагранжеву координату а частицы, находящейся на поверхности, из того условия, что -а является временем, в которое частица занимает положение Zo. Чтобы перейти от положения г, к 2, для всех частиц требуется одно и то же время Р при установившемся движении. Следовательно, функция z=f(a, Р -а) не должна зависеть от а для каждого р. Отсюда

z = /(a, 0=2(р), р=а + /. (1)

Уравнение (13) в данном случае примет вид

z -2eV-f 1=0. (25)

Полагая здесь ф = О и затем решая полученное уравнение относительно производной, получаем

Тогда из формулы (4) п. 11.60 следует, что величина г (а, /) = = {ftt + igyifa должна быть функцией только от р, т. е., например,

г(а, 0=5(Р). (2)

Тогда уравнение (4) п. 11.60 сводится к обыкновенному дифференциальному уравнению вида

zm + ig=iS)z(P), (3)

где S (Р), а следовательно, и S (Р) являются действительными для действительных значений р. Это линейное дифференциальное уравнение можно решить относительно г(Р) двумя квадратурами.

Если движение безвихревое, то из формулы (3) п. 11.61 следует, что W также является функцией от p = a-f-/. Эта функция определяется с помощью квадратуры из уравнения

=-7Wzm. (4)

Таким образом, можно сделать важное замечание. Если в уравнении (3) положить g =0, то получим задачу, в которой отсутствует сила тяжести; такого вида задача уже рассматривалась в этой главе. Найдя функцию Zo (Р) - решение этой задачи без силы тяжести, мы получим дополнительную функцию из линейного уравнения (3), когда g=0, а именно

iS (Р) = г; (p)/z; (Р), когда g = 0. (5)

Подставив эту функцию в уравнение (3), получим уравнение

z m + ig = /(), (6)

решение которого можно представить в виде

z.(P)=2o(P)-b{f {P)-f (0)}, (7)

где F(P) -частный интеграл уравнения (6). Так как уравнение (6) аналогично уравнению (3), то функция Zi(P) задает свободную поверхность постоянного давления, которая сводится к функции Zo(P) при = 0.

Точно так же решение Zi (Р) содержит свободный параметр, а именно поверхностную скорость в решении Zo(P).

Будем называть Zi (р) касательным решением) данной задачи, так как она сводится к задаче без силы тяжести, когда =0.

11.64. Касательное решение для струи, направленной вертикально

вниз. Рассмотрим струю, направленную вертикально вниз и вытекающую из отверстия шириной 2а в плоской горизонтальной бесконечно длинной пластинке, как изображено на рис. 201. Выберем начало координат не в точке В', а в середине отрезка ВВ и рассмотрим свободную линию тока ВС .

Для этой свободной линии тока мы имеем на основании формулы (28) п. 11.62 параметрические уравнения

x,= *(ln-bsin0), z/o=*(-lnctgi-e-bcose. *=2а/(я-ь2). (1)

где через 6 обозначен острый угол между направлением движения и вертикалью, так что e = Vtn в точке В и 6 = 0 в точке Сое.

) М11 пе-Th omson L. М., Ргос. Midwestern Conference on Solid and Fluid MKtoiics. 1959.

Пусть (/ - скорость частиц на поверхности струи и Р-время, необходимое для того, чтобы частица передвинулась вдоль свободной линии тока от точки В к точке Р. Тогда

f/*=2;(P);(P). (2)

и из формул (1) получим

Zo(e) = A{ln + sine + Jcose- ilnctge} . (3)

Дифференциальное уравнение, которому удовлетворяет касательное решение (6) п. 11.63, можно с учетом формулы (2) записать в виде

Заменяя переменное р на 6, получаем откуда

таким образом, находим

в

2{e)=A2o{Q)+B- [ 2;(e)2o(e)de. (5)

Мы должны положить у4= 1, В=0, и поэтому

2i(e)-2o(e)-/g [/(е)-(1я)] . (6)

После интегрирования получаем

2i (6) = 2о (6)-Ь- {е-1-4 / (in ctgi)4 In ctg 1} . (7)

Замечаем, что In ctg6 = 00 при 6 = 0, но

lim (sin О In ctg 1 в) = 0. (8)

Из формулы (7) имеем

x = xo-b-f{e-f + sin01nctg-} =

= А {i-hsinO}-h (0-f-h sin 0 In ctg 4) .

следовательно.

Это уравнение определяет асимптоту свободной линии тока касательного потока.

О)гласно уравнению неразрывности, через каждое поперечное сечение струи в одно и то же время должно протекать одинаковое количество жидкости, и так как скорость стремится к бесконечности, когда 0->-0, то в бесконечности поверхность струи будет стремиться совпасть с этой асимптотой.

В частности, выберем поверхностную скорость такой, чтобы выражение (9) обращалось в нуль, т. е. чтобы

Ugk. (10)