будет существовать. Возьмем эту точку за начало координат, ось х направим параллельно направлению потока Ai.

Свободные линии тока AiBi, BiAt А^Вг, BAi являются линиями постоянной скорости, и, следовательно, скорость всех четырех струй в бесконечности должна быть одинаковой и равной U. Пусть ht, h ku к, обозначают ширину на бесконечности каждой струи А^ А В^ В^. Из условия непрерывности получаем

Л +А. = (1)

Здесь величины Ai и Л, заданы, величины kt и kt неизвестны.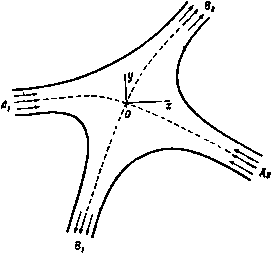

г-пйосмаоь

Рнс 195.

11.31. Комплексная скорость. Если написать, как обычно,

v = qe- = u - iv,

Tjifi 9 -величина скорости, а угол 6 определяет направление скорости, то на свободной линии тока выполняется равенство

г = С/е-<в. (2)

Следовательно, когда мы обходим свободные линии тока, выходя нз точки Ai и описывая по очереди линии AiBi, ВИ, AtBx, BtAi, то угол 6 при этом изменяется от О до - 2я; значит, угол -в при этом наменяется от О до 2п.

Следовательно, изображающая точка будет описывать на векторной диаграмме в плоскости V окружность радиуса U с ентром в начале координат (рис. 1%).

Тогда точки Ль Л], Bi, В^ можно представить в виде

а. = С/. а. = {УеЧ

где -а, - р, - Y-углы, определяющие направления струй Л„ Bi, В, бвооаечности. Здесь величина а задана, а величины Р и у неизвестны.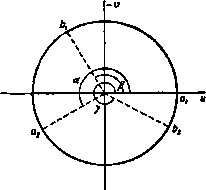

о-плоскоап

Рис. 196.

Величины расходов жидкости в струях Ai, At, Bi, Bt соответственно равны

Ыи, hJJ, kiU, kJJ,

следовательно, если положить ф=0 на линии AiBt, т. е. на дуге а^Ь^, то будем иметь

=hiU на дуге afii,

ф = (Л, Аз)(/ на дуге М .

= kJJ на дуге ajbf

11.32. Выражение комплексного потенциала через комплексную скорость . Для определения комплексного потенциала а = ф-Ь<Ч|>, удовлетворяющего полученным выше условиям, воспользуемся тем, что ф является действительной частью величины -iw. Следовательно, можно применить формулу Шварца (см. п. 11.20), согласно которой получаем соотношение

= -e-2iln(l/e*e-t)) =

= -e-2/lnl/e*e-2iln (l-) =

= e-2/ln(l-)-2/lnl/,

где логарифм определен таким образом, чтобы при v = 0 он обращался в нуль. Следовательно,

=Л.{р-2/1п(1-) + 2/1п(1-)}--

+ (*.-Л,){(а - Р)-2iln (1 -1-)+2Пп (1 - )}

+ A,{(Y-a)-2/ln(l-)+2/ln(l-)}.

Поэтому, отбрасывая константу, получаем

,п(1-)+*., (1-)-

-*.1пО-)-*.1п(.-)}.

что представляет собой искомое выражение комплексного потенциала через ктатлексиую скорость .

11.33. Соотношения между шириной и направлением струй. Так как

количество движения жидкости в проекциях на оси х л у сохраняется, то мы имеем

hi +A,cosa -*i cosP -А1СО5\ = 0, ht%\na-ki sinP -/Sssin Y=0.

11.34. Выражение величины z через комплексную скорость v. Так как

то мы получаем

J 1 j I dw J

dz=--dw=--dv.

Далее, из п. 11.33 имеем

I dw и v dv n

Al i f*2 *1 *2 1

. (ai - ) (02-Ю) D(6i -D) D(*2

я \ai Oi-v 02 02-v bi bi-v bz bz-v}

~ ЯМ \ai ~ oz bi bzi

Согласно п. 11.33, второй член в правой части этого равенства обращается в нуль. Учитывая, что z = 0 при v = 0, мы получаем после интегрирования формулу

-{ir4-i> 0-i)-4-i)-t4>-a-

где

ai = U, at = Ue*, bi = Ue* , b, = Ue*y.

Отсюда следует, что движение обратимо, так как полученная формула для величины г не изменится, если изменить знаки у величин U, щ, (ц,

11.35. Уравнения свободных линий тока. На свободной линии тока

= С/е- .

Подставив это выражение в вышеполученную формулу для величины г, мы находим

Я2 = Ai In (1 - е- ) + A-ia In (1 - e-ie-la) - In (1 е-<в-ч ) *-iv in (1 -е-*в-*т).

l-e-*x = e 2(e2 e 2) = 2/sin--e 2.

Следовательно,

Я2- Л, {in 2i + In sin I-y} + te-** {in 2* + In sin- - i -

- kie-V {In 2/ + In siniifi- - i Ц^] -

Теперь, согласно п. 11.33, получаем

Таким образом, находим

я2 - (- Ме-* +ftipe- +*.Y -*) +

+At In sin I + A.e-*Mn sin - In sin - ft,e- v In sin .

Приравнивая действительные и мнимые части в обеих сторонах уравнения, мы получаем координаты (дг, у) точки свободной линии тока, выраженные через параметр 6.

11.40. Неопределенность задачи. При решении задачи о двух соударяющихся струях мы ввели четыре неизвестные величины, а именно: Ai, кг, Р, Y - асимптотические значения ширины и направления струй, получающихся в результате соударения двух струй. Были найдены три соотношения в пп. 11.30 и 11.33, связывакнцие эти постоянные величины, так что задача содержит одну неопределенную величину. Таким образом, в общем случае единственного решения не существует. Эта неопределенность, несомненно, связана с тем, что мы рассматриваем уже сформировавшееся установившееся движение, не учитывая начальных условий, которые приводят к изучаемому установившемуся движению.

В самом деле, вш можем предположить, например, что изучаемое движение формируется в результате пуска струй в различных тспжях в различные моменты времени с промежутком времени t. Несомненно, что различным значениям времени t будут соответствовать различные установившиеся движения, хотя и нет основания предполагать, что все они будут устойчивыми.

11.41. Прямой удар двух одинаковых струй. В этом случае имеется симметрия относительно обеих осей координат (рис. 197), так что мц можем положить

а = я, Р-Y=-. Ai=:A,= Ai = А, = А.

Рис. 197.

Иа последней формулы п. 11.32 следует

так что

[ln(l-i) + ln(l+)-

-Ч'-)- (+ж)]-

Далее, из последней формулы п. 11.34 находим

(1) (2)

Исключая величину из формул (1) и (2), получаем соотношение между величинами w и г.

На свободной линии тока v = Ue-. Следовательно,

-2.-.Лз1п(-4) 2./(Н)з1п(-)

= 1п---i\n--i-

2.-fcos( ) 2H)cos(f-)

= in(-/tg)-nn(-ag(bJ)).

Лалее, на линии тока в первом квадранте имеем

-<в<-л. Если положить вв-л -X. то 0<х<у. тогда

-=ln{ ,tg( +l)}-nn{-.tg( + )} =

= In(.ctg-)-.ln{/ctg( + )} = = In i-1 lni + Inctg I - j In ctg

= -- -~- + lnctg-bnntg( + ) . Таким образом, если t = tg, то

J Ir. * 1 / i* Lin

следовательно, после исключения t имеем Таким образом,

(-.)i..nclh( ,), ,. +Л, сШ(-),

Если рассматривать линию тока х = О как твердый барьер, то мы имеем решение задачи о прямом ударе струи о бесконечную плоскость (рис. 198).

Полную силу давления иа плоскость (иа жидкий элемент единичной толщины) можно получить путем интегрирования давления. С другой стороны, полную силу давления жидкости можно получить иным путем. Количество движения, переносимое в единицу времени струей, перпецднкулярной стенке.

равно qAC/, а количество движения жидкости, текущей вдоль стенки, не имеет составляющей по нормали к стенке. Таким образом, полная сила давления

равна qW*.

Следует заметить, что в вышеуказанном решении нет неопределенности, так как условие симметрии дает для неизвестных величин четвертое соотношение.

11.42. Прямой удар двух неодинаковых

струй. Если сталкиваются две струи с различной скоростью, нос одинаковыми асимптотами, как это изображено на рис. 199, то ясно, что должно существовать симметричное решение. В данном случае

Ри198. ki=kt, а=п. у = 2я-р.

Отсюда, согласно п. 11.33, получим

*1 = (*1 + *2) = I (А| + /Ц). А, - А - Ai cos р - А, cos р = 0.

Таким образом,

cos В^Ihiibihizh

Параметрические уравнения свободных линий тока могут быть найдены указанным ранее способом.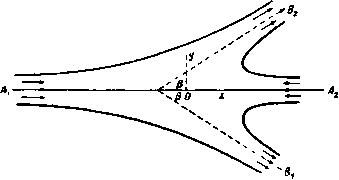

Рис. 199.

11.43. Косой удар двух одинаковых струй. Если две струи одинаковой ширины с асимптотами, наклоненными под углом 2р, были выпущены одно-BpcaieHHO, то физически ясно, что существует решение, симметричное относительно биссектрисы угла между двумя асимптотами. Далее, из принципа обратимости (см. п. 11.34) следует, что решение будет таким же, как в предыдущем пункте, если мы повернем все скорости иа 180° (рис. 199). В данном случае Ai = А|, р задано, а величины At, А2 требуется определить.

Теперь мы имеем

Ai-fA, = 2A

А, А,= (Ai + A,)cosP = 2AiCos р.

Таким образом,

A, = Ai(l+cosP), A,==Ai(l-COS Р).

11.50. Твердые границы. Рассмотрим теперь движение жидкости, при котором движущаяся жидкость ограничена частично свободными линиями тока, частично неподвижными твердыми стенками.

Твердая стенка, служащая границей, конечно, является линией тока, вдоль которой 1) = const, но не обязательно является изобарической или изотахической линией.

Те задачи, в которых твердые границы прямолинейны, можно исследовать по методу Кирхгофа. В этом методе в основном используется следующая функция:

где f/ -характерная скорость, обычно равная поверхностной скорости на свободной линии тока. Так как

- - = ы - jy = е- 9 = V,

Q-. (f)- (H)+,e.

Вдоль свободной линии тока скорость U постоянна, следовательно, величина In (U/q) также постоянна.

Вдоль неподвижной прямолинейной границы направление движения, задаваемое углом 6, постоянно, так как оно совпадает с направлением границы.

Следовательно, если мы изобразим границы и свободные линии тока в плоскости Q, то годограф будет состоять из прямых линий и образует многоугольник, внутренняя область которого может быть отображена с помощью преобразования Шварца - Кристоффеля на верхнюю половину плоскости t,. Таким образом, получается соотношение между величинами Q и 5, т. е. между величинами dw/dz и t,.

С другой стороны, границы и свободные линии тока, изображенные в плоскости W, соответствуют прямым линиям ф = const; полученный многоугольник также можно отобразить на верхнюю половину плоскости 5 Это приводит к соотношению между ш и

Если из двух найденных таким путем соотношений исключить величину 5. то мы получим соотношение между dw/dz и ш, откуда после интегрирования получим соотношение между величинами w ч z, которое характеризует движение.

Часто бывает удобно оставлять величину J в качестве параметра, через который выражаются ш и z.

В последующих пунктах вышеуказанный метод будет применен д^я решения частных задач.

11.51. Плоская форма насадка Борда. Насадок Борда состоит из длинной прямолинейной трубкн, вдающейся внутрь большого сосуда.

Если пренебречь силой тяжести, то отношение площади сечения текущей воды в самом сжатом месте к площади сечения трубки равно Уг. Следовательно, насадок Борда плоской формы состоит из длинного канала, параллельные стороны которого вдаются внутрь сосуда. Будем считать канал настолько длинным, что стенки сосуда не оказывают влияния на поток жидкости; фактически мы рассматриваем бесконечно длинный канал.

На диаграмме в плоскости z (рис. 200) показано сечение насадка, имеющего стенки ЛооВ, А'ооВ'. Стенка АссВ частично является линией тока. Жидкость течет вдоль линии АооВ, поворачивается в точке В и вытекает из трубки вдоль

линии ВС . В заштрихованной области между линиями Л ,В и ВС находится неподвижная жидкость или совсем нет жидкости. Линии, соответствующие омываемым стенкам в плоскости z, отмечены на всех диаграммах специальной штриховкой.

В сечении СовС имеется равномерный параллельный поток, текущий, допустим, со скоростью и. Пусть ширина насадка в сечении ВВ равна 2а.

Z-плоскость * U-

плоскость

llllllllllllimilllllimniiin

у

V/и-плоскость

Q - плоскости

с

9-х

в-О

Рис. 200.

Если о - коэффициент сжатия, то ширина вытекающей струи равна 20а, я поток, вытекающий из насадка, равен 2oalJ.

Центральная линия тока Всо/ является прямой линией. Если на B.F. мы возьмем ф = О, то на линии тока ЛооВСсо будем иметь ф -= -oaV, и на линии тока Л^ВС будем иметь ф = oaV.

Пусть ф = О в точках В и В'. Это всегда возможно, так как потенциал скорости определен с точностью до аддитивной постоянной. Тогда в точках Л^, Лоо, Boo и во всех точках сосуда на большом расстоянии от ВВ получим Ф = -- со, в то время как в точках Coi получим ф = - оо. Таким образсш, плоскость W имеет вид, изображенный на рис. 200.

Отобразим внутреннюю область многоугольника Л^С С ,Лов плоскости w на верхнюю половину плоскости t,. Причем точкам В', В соответствуют точки 5= -1> 1> а точкам С , С , которые совпадают в бесконечности, соответствует точка 5 = 0. Тогда нз формулы (2) п. 10.32 получим

w=ln-iaaU, (1)

при этом предполагается, что при 5 = I логарифм обращается в нуль.

Следующий шаг состоит в том, чтобы построить многоугольник, соответствующий формуле

Q=, (-0 = , (!) = , + .e.

когда точка z описывает границу в плоскости г. Далее следует отобразить этот многоугольник на плоскость 5-

Для того чтобы проследить изменение угла 9, когда точка z описывает границу, изобразим диаграмму на вспомогательной плоскости, задаваемой формулой

На свободной линии тока q=U, следовательно,

Таким образом, когда мы движемся вдоль линии ВСсоС^В', комплексная величина U/v описывает окружность единичного радиуса. Вдоль линии АооВ мы имеем 9 = 0, на той же линии величина д увеличивается от О в точке Аоо АО и в точке В. Следовательно, величина U/v уменьшается от оо в точке Аоо до единицы в точке В.

Соответствующая диаграмма изображена на рнс. 200. Линии АооВ, А^В' в действительности совпадают, но для ясности они изображены в виде двойных линий. Теперь оказывается, что 9 = 2я вдоль линии А' В', следовательно,

8=0 на АооВ,

Q=/9(0<9<n) на ВооС,

Q = /9 (я < 9 < 2я) иа С, В',

9 = 2я на В'А'оо.

Соответствующая диаграмма в плоскости д изображена на том же рисунке.

Отобразим многоугольник, расположенный на плоскости 5> с помощью формулы п. 10.31, которая дает

Q=2Arch5 = 2 1n(C-b/r=n). (2)

так что

Формулы (1) и (3) дают решение рассматриваемой задачи. Мы можем исключить величину 5 нз этих формул, а потом с помощью интегрирования получить соотношение между величинами w н г. Представляет интерес определить вид свободных линий тока, что будет сделано в следующем пункте.

Относительно вышеуказанного решения следует заметить, что в соответствующем потоке нет точек, в которых скорость становилась бы бесконечной. Лб1ДКость обтекает углы в точках В vi В' с конечной скоростью; получаемое решение оказывается физически приемлемым.

В реальной жидкости застойная область обычно заполнена жидкостью, имеющей вихревое движение. Следовательно, вышеуказанное исследование можно рассматривать только как первое приближение. С другой стороны, полученное решение дает представление о вытекающей струе, если область вне свободной линии тока заполнена воздухом или водяным паром.

11.52. Уравнение свободных лнрий тока. Сделаем следующие общие замечания.

(I) На свободной линии тока величина С действительна, так как линия тока отображается на действительную ось плоскости £.

(II) На свободной линии тока dz=dse*, где угол 6, как обычно, указывает направление касательной, а ds-элемент дуги линии тока.

(III) Если (х, )-точка на свободной линии тока, то

f=cose, f = sine.

(IV) На свободной линии тока Q = (6.

(V) Если (/ - постоянная скорость вдоль свободной линии тока, то

-и

е*в|= 1.

Из замечаний (V) и (I) следует, что на свободной линии тока выполняются равенств

и

dz Ud

d dm

e*ds и HI dl dm

, ds

причем берется знак + или -. смотря по тому, увеличивается ли величина S вместе с увеличением С вли нет.

Вышеуказанные замечания применимы ко всем задачам, которые решаются так же, как и задача о насадке Борда.

Для применения этих замечаний к данной задаче возьмем за начало координат точку В плоскости г и рассмотрим свободную линию тока ВС . Когда мы идам вдоль этой линии от точки В в плоскости z, то величина С уменьшается от 1 до О в плоскости Следовательно, производная ds/d отрицательна. В силу формулы (1) п. 11.51 имеем

ds 5с

и

К ds

2аа *

Далее в силу замечания (IV) из формулы (2) п. 11.51 получим

(6 2 Arch С.

Таким образом.

C = ch

е

= COSy

и dC= -Isin-Jde.

Следовательно, в силу формулы (1) имеем

ём аа. в