и

- f.

Рис. 187

цилиндр с прямоугольным поперечным сечением, расположенный симметрично между двумя параллельными стенками, как показано на рнс. 187.

Читатель может убедиться, интегрируя выражение Ytqq* вдоль отрезка DD, что сила, действующая на этот отрезок, будет конечной. Это можно сравнить с соответствующим результатом, полученным в конце п. 10.60.

10.80. Канал с разветвляющимся руслом. На рис. 188 изображен канал с разветвляющимся руслом, причем стенки основного и ответвляющегося русла являются прямыми параллельными линиями. Стенки ответвления образуют угат а со стенками основного канала.

Ширина канала и его ответвления обозначены соответственно через h. hi, hi, скорость течения в бесконечности в верхнем бьефе основного канала равна и. Наша задача состоит в определении скоростей течения UiK UzS нижнем бьефе основного канала и в его ответвлении.

Линия тока /, идущая из бесконечности, разветвляется в критической точке С на две линии, СВ и СО . Жидкость слева от / втекает в ответвле-

Интегрирование упрощается, если положить С = -гз7Г' 6 = р = .

отсюда так что

dz ь, / 2 2 4

откуда находим

где L - произвольная постоянная. Если допустить, что точка г = 0 соответствует точке £(С = а), то тогда / = 0 и поэтому L = 0. Подставив значение С в формулу (2), получим

Исключая переменное t из формул (3) и (4), мы получаем связь между величинами W и Z.

Принцип отражения позволяет, кроме того, применить тот же комплексный потенциал для построения потока, обтекающего бесконечный твердый

h У --г I

1 <

2-плоскость

-о -ft I с

о.Ш?7777777?7777Ш77777777777777:т ABCD

li-плоскость

Рис. 188.

Пусть точкам Л , В , О соответствуют точки = -а, -Ь, с соответственно. Заметим, что границе основного канала соответствуют отрицательные значения

Рассмотрим теперь формулу

Q = In = In у -f 9, где X, = qe-\

Вдоль сторон основного канала 0=0; вдоль сторон ответвления 0 = о. В точке С имеем = О, следовательно, величина Q обращается в бесконечность в этой точке. Таким образом, в комплексной плоскости Q мы получим область, изображенную иа рис. 189.

в

e-ar

ТТТТТТТГТТГГТТТГТТГ^ Cm

л в

о плоскость

Рис. 189.

Отображая плоскость Q иа плоскость I, согласно п. 10.32, получим

;=-.-о /.= () . (1)

В этом случае мы имеем следукхцее соответствие между величинами С и v:

I -а -b с

ние, а справа от / течет по основному каналу. На линии тока AnED поток претерпевает резкое изменение направления в точке £, где скорость соответственно обращается в бесконечность.

Отобразим теперь внутреникио область канала на плоскость так, чтобы точка £ перешла в бесконечность, а точка С перешла в точку t = 0.

поэтому

Uh = Uiki+Uth,. (3)

Этот результат можно получить также из уравнения неразрывности.

Положив ф = 00 в точке Л , получим, что ф = - оо в точках Всо и Оо..

ш-плоскость Ряс. 190.

Таким образом, мы получаем требуемую область, которая изображена на рис. 190.

Для отображения плоскости w на плоскость С находим

= AC.t (5 + аГЧС + 6Г -с)- = Kia 1 Кф 1 К,с 1

отсюда, интегрируя и делая небольшие преобразования, получаем формулу

Далее на линии D E функция ф = 0, а величины (4,+а), (С -с) имеют одинаковый знак. Поэтому соответствующие значения лога рифмов будут действительными и величина Li также должна быть дейст вительной. Кроме того, ф = 0, ip=Ut и С = 0 в точке С. Таким образом константа Ц должна быть величиной чисто мнимой. Отсюда заключаем что L, = 0; полагая С = О, получаем

Ff t Kfon Kjbn

tha-b)a+c) (a-b)(b+c)-

Наконец, вдоль линии ЛооВоо имеем = Uh, в то время как величина <С + а) положительна, а величины (5 + &), (С -с) принимают отрицательные значения. Поэтому

... К^ая

Таким образом, получаем

=() -. с^ОУ . (2)

Для построения соответствующей области в плоскости w примем, что прямой ф=0 соответствует линия ЛооЕО . Тогда получим

Отсюда и из формулы (3) имеем

(а-Ь)(Ь+с) следовательно.

Далее, из формулы (1) получаем

=1)=(Уе-(5)

из формулы (4) находим

dwUh 1*1 1 Vihi - Vh 1

отсюда путем деления получим производную dzld как функцию величины С-Теперь уже обычным путем определяем выражение w, которое дает распределение скоростей в зависимости от г.

Так как и = 0 при С = 0, то производная dwldi также обращается в нуль при С = 0, следовательно, из формулы (6) имеем

Uh Uthi , Uh-Uthj a b с

Отсюда, применяя формулы (3) и (2), находим

или

Пусть J = . = 1*. 1 = X. тогда

Рис.191. ¥4- *-! Чг -1

Первый из этих результатов получается из формулы (3). Подстановка двух последних соотношений в формулу (7) дает равенство

В рассматриваемой задаче величины Я, ц, а являются заданными, а значение % приближенно определяется из последнего трансцендентного уравнения.

Применение принципа отражения показывает, что полученное решение дает возможность решить задачу о прямолинейном канале с двумя ответвлениями в точках С и С (рис. 191). В данном случае начало координат удобнее перенести в среднюю точку отрезка СС.

ПРИМЕРЫ К ГЛАВЕ 10

1. Применяя преобразование Шварца-Кристоффеля, показать, что комплексный потенциал т, определяемый форму.юй

tB =L ( --c ),

дает решение задачи обтекания неограниченным потоком, имеюшим на бесконечности скорость I/, бесконечно тонкого препятствия длины с, перпендикулярного прямолинейному берегу бесконечной длины-

Примеры 09

Найти давление в произвольной точке препятствия и показать, что оно становится отрицательным, если j,>c(l-j-*)*(l+2ik)~ : при этом k = nU*f2po, где давление в бесконечности.

2. Доказать, что комплексный потенциал вида

а>= - imn+m In ch -

описывает течение жидкости в сосуде, если в стенке сосуда имеется небольшое отверстие, через которое жидкость вытекает. Отверстие расположено на высоте h от дна сосуда. Сосуд имеет бесконечную высоту и ширину а. Линия тока ф=0 идет по стенке, на которой нет отверстия, по дну и по второй стенке до отверстия. Показать, что иа достаточно большом расстоянии от отверстия имеет место поток, параллельный стенке.

3. Показать, что комплексный потенциал вида

a)=ffllnsh{nz/(2a)>

дает поток в бесконечно большом сосуде шириной 2а, если в сосуде имеется небольшое отверстие, сделанное в середине дна сосуда, через которое вытекает жидкость. Изобразить общий вид линий тока и доказать, что на расстоянии, превышающем ширину сосуда и отсчитываемом от дна, поток будет в основном параллельным стенкам сосуда.

4. Доказать теорему Шварца -Кристоффеля об отображении многоугольника на полуплоскость. Что будет в случае, когда один из внешних углов многоугольника больше 2л?

Жидкость течет по насадку шириной 2Ь, к которому симметрично примыкают два к.1инообразных канала, ограниченных прямолинейными стенками, заданными уравнениями

±у=&+дс1вРя. дс>0; ±j,=fr-actgpn, дс<0.

Если расход жидкости (отнесенный к единице толщины) в насадке равен 2bV, то показать, что течение определяется соотношениями

bV . t-l dz .,

где

о=1--р.

5. Решение какой задачи задается формулами

Ф+ф=1п(/-а).

где x и I/ -декартовы прямолинейные координаты, а <р и ф-соответственно потенциал скоростей и функция тока?

6. Найти формулы преобразования для двумерного течения в реке, русло которой je.-iat-T поворот на девяносто градусов. Русло образовано положительными полуосями к<юрз1М1,1т дг и у и прямыми линиями

*=в, у>а и у=а, х>а.

Скор(1сть течения в бесконечности равна 2JU.

7. Показать, что формулы преобразования

r = {v/Tiri Arcsec/]; t = e ,

где г = х {-ifi. w= p4-i4(i, дают потенциал скоростей <р и функцию тока ф, соответствующие течению в реке шириной а с прямолинейными берегами, имеющему скорость V в бесконечности и впадающему под прямым уг.том в поток, ограниченный только прямолинейным берегом. Считая поток двумерным, показать, что действительная ось в плоскости I соотиетствует всей границе жидкости.

Xsiniq.)/*

где h и 2ik -длина и ширина прямоугольного выступа. Получить полное решение задач без использования эл.1иптических функций, считая А = 0.

8. Показать, что решение задачи о потоке, имеющем скорость V в бесконечности и ограниченном только одним прямолинейным берегом с прямоугольным выступом, дается формулой

йг 1 (ш - с ) dm V (а -

где Ь и г-константы, определяемые уравнениями

F{clb) к

р {ytfl-сЧЬ) h

и

Здесь

Глава и СТРУИ И СТРУЙНЫЕ ТЕЧЕНИЯ

11.10. Свободные линии тока. Линия тока \i в двумерном движении делит жидкость на две области А н В. Если пренебречь внешними силами, то для невязкой жидкости в случае установившегося движения на лиинях тока обеих областей имеют место равенства

Здесь индекс обозначает данную область. Рассмотрим точку Р линии тока Если мы будем приближаться к точке Р из области А, то значение давления в этой точке будет равно pi, а значение скорости будет равно qi. Точно так же, если будем приближаться к точке Р из области В, то получим значения рг и qz. Таким образом, имеем

Далее, в силу непрерывности давления (см. п. 3.31) имеем pi = рг. Отсюда следует равенство

QAql-QBqi= const.

В случаях, которые мы рассматривали до сих пор, скорость была непрерывна, т. е. qi = qz.

Теперь мы рассмотрим класс движений, для которых скорость жидкости разрывна, например слой нефти (масла), плавающий по слою воды, при этом скорости в обоих слоях различны.

Уточняя характер разрывного движения, предположим, что жидкость в области А находится в покое, т. е. qi = 0.

Тогда мы видим, что вдоль линии \i скорость qz = const. Таким образом, мы приходим к следукицему определению. Линия тока, отделяющая движущуюся жидкость от покоящейся, называется свободной линией тока.

Если пренебречь внешними силами, то в этом случае свободная линия тока обладает следующими свойствами:

1) Вдоль свободной линии тока функция тока ф постоянна. Это, конечно, общее свойство всех линий тока.

2) Свободные линии тока являются изотахами, или линиями постоянной скорости. Скорость вдоль свободной линии тоже будем называть поверхностной скоростью.

3) Вдоль свободной линии тока давление постоянно. Таким образом, свободные линии тока являются изобарическими линиями, или изобарами, т. е. линиями постоянного давления.

Доказательство. Так как давление непрерывно, то его значение на свободной поверхности равно значению в той части примыкающей жидкости, которая находится в покое, а это значение постоянно, если пренебречь внешними силами.

Из свойства 3) следует, что свободные линии тока могут существовать, когда покоящаяся жидкость отсутствует.

Пример. Жидкость, вытекающая в виде струи из отверстия в сосуде, имеет границы в виде свободных линий тока, причем постоянное давление вдоль свободных линий тока поддерживается благодаря наличию атмосферы. Если бы не было атмосферы, то постоянное давление равнялось бы нулю.

П.П.Струи и струйные течения. Пренебрегая внешними силами; предположим, что мы имеем жидкость, движущуюся в двух измерениях, ограниченную свободными линиями тока Цг- Эти линии тока делят плоскость на три области А, В, С, причем движущаяся жидкость занимает область В. Если

В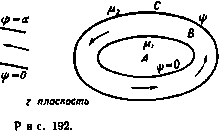

области i4 и С не содержат жидкости, то мы имеем струю; если области А и С заняты покоящейся жидкостью, то мы имеем струйное течение. Дым, выходящий из трубы, или вода, вытекающая из шланга, являются примерами (трехмерных) струй. Примерами струйных течений являются вытекание жидкости в бассейн из затопленных труб или океанские течения, например Гольфстрим.

W-плоскость

Рис. 193.

i-плоскость

Струя или струйное течение могут быть замкнуты и могут распространяться до бесконечности (рнс. 192).

На свободных линиях тока величины ф и постоянны.

Пусть ф = 0, q = U на линии тока ц, и пусть ф = а, q = V на лннни тока Ца.

Тогда область в плоскости w представляет собой бесконечную полоску, заключенную между прямыми ф = 0 и ф = а (рис. 193).

Если мы отобразим область плоскости w на верхнюю половину плоскости С таким образом, чтобы точке а'=0 соответствовала точка С=1, то, согласно п. 10.32, мы получим

ш = 1пС,

причем ветвь логарифма выбрана так, что значение логарифма обращается в нуль при С = 1-

Рассмотрим теперь функцию ш, положив

~ и d2~

так что

© = e + iln-j-.

Мы имееы q = U на линии Ц| и q=:V на линии (ij; следовательно, 0=6 на линии ij и (0=64 iP иа линии (it, где

Р = 1п^.

Таким образом, область в плоскости ш имеет почти такой же вид, как и область в плоскости w; она состоит из полосы шириной р, которая ограничена с одной стороны действительной осью (рис. 194).

Отображая эту полосу на плоскость 5> получаем (см. п. 10.32)

ш=1п£. (3)

где © = 0 соответствует значению 5=1.

Следовательно, из формул (1) и (3) находим

учитывая формулу (2), получаем

Если U = V, то Р = О и, таким образом,

w= -Vz.

Это означает, что струя, имеющая одинаковую скорость на обеих границах, должна быть прямолинейной.

Если PtO, то из формулы (4) получим

.-..--,ехр(!?).- р(-Й).хр(-Й).

Следовательно,

2-го! = р/ехр(-).

Это значит, что если величина ф постоянна, то 2 -Zo постоянен и точка г описывает окружность с центром в точке Zq. Радиус этой окружности равен

шехр(-й).

а pt7

Следовательно, если г, и rj-радиусы окружностей fii и Ц], то имеем

;-1 = ехр (Р) = .

т. е. скорости течений иа свободных линиях тока обратно пропорциональны их радиусам.

Таким образом, оказывается, что могут существовать течения, ограниченные свободными линиями тока, причем эти линии тока представляют

собой либо параллельные друг другу линии, либо концентрические окружности. Следует заметить, что в последнем случае при безвихревом движении жидкость не вращается подобно твердому кольцу.

11.20. Формула Шварца. Если дан круг радиуса R с центром в точке г = 0, то функция f {г), аналитическая внутри данного круга, действительная часть которой принимает на окружности значение (р(0), определяется с точностью до значения мнимой постоянной формулой

/(2)=2ф(в)йв. (1)

Доказательство. Пусть J=/?e*9 обозначает точку на окружности С круга.

Тогда С=/?е-*в = /? /. Так как в =-/ In (С ?), то мы можем написать

ф(в)=Ф(С). (2)

где ф (С) - известная функция от Тогда на окружности имеем

/(С)+7(/?*/С)=2ф(в) = 2ф(0 (3)

и, следовательно,

(С) * (С) * (б)

Если точка г находится внутри окружности С, то, используя формулу Коши (п. 5.59) и теорему о вычетах, получаем

/W-i-7(0)=2Si \ (5)

Пусть / (0) = а + ib, тогда / (0) = а - ib; таким образом, полагая в формуле (5) 2 = 0, получаем

следовательно, из формулы (5) находим

() = 2S t(C)dt + /6. (7)

Цолагая С = Re, мы имеем dllX, = < dQ, отсюда вытекает требуемый результат.

Часто бывает полезно применять формулу (5) вместо формулы (7).

11.30. Соударяющиеся струи. На рис. 195 показаны две равномерные струи i4i и Аг, имеющие в бесконечности одинаковую скорость U, встречающиеся и распадающиеся на две другие струн fii и В^. Предположим, что установившееся движение описанного типа существует, задача состоит в том, чтобы определить струи Bi и В , если струи А^ и А^, полностью известны.

Если предположить, что струи Ах и Ai набегают из бесконечности, то физически возможно, что они встретятся в критической точке О. Следовательно, если движение остается установившимся, то критическая точка