различные конечные точки В и С; в последнем случае мы получим полуплоскость, аналогичную той, которая получается из диаграммы рис. 173 (/).

Этот интуитивный метод может быть применен для изучения конкретных задач только в простейших случаях, однако ои позволяет выяснить картину преобразования потока.

Таким образом, если мы имеем равномерный поток в канале с параллельными плоскими стенками, то линиями тока являются прямые, парал-

Рис. 175.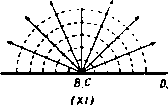

лельные стенкам, а линиями равного потенциала скоростей являются прямые перпендикулярные стенкам. Равномерный поток можно рассматривать как поток, обусловленный источником в -оо и стоком в -Ь 00. Если мы развернем канал, считая, что точки В и С совпадают, то получим источник в точке В, С и сток в бесконечности (рис. 175 (X-X/)]. Хотя этот результат вполне очевиден, он хорошо иллюстрирует процесс преобразования потока.

10.20. Теорема Шварца - Кристоффеля. Пусть а, Ь,с, ... представляют собой л точек действительной оси плоскости Z причем а < b < с ....

Ь, b b, плоскость

г-плоскость Рис. 176.

Пусть а, р, у. ...-внутренние углы простого замкнутого многоугольника с п вершинами (рис. 176), прн этом

а-ЬР + у+--- =(п-2)я.

Тогда теорема Шварца - Кристоффеля формулируется следующим образом.

преобразует действительную ось плоскости С в границу замкнутого многоугольника плоскости г так, что вершинам многоугольника отвечают точки а, Ь, с, а внутренними углами многоугольника являются

а, р, Y ----Кроме того, если многоугольник простой, то его внутренняя

часть соответствует при этом верхней половине плоскости С- Постоянная величина К может бьипь и комплексной.

Доказательство. Доказательство теоремы в основном заключается в установлении следующих утверждений:

1) Когда величина J увеличивается, например, от а до 6, то величина z описывает прямую линию.

2) Когда величина проходит через точку Ь, эта прямая поворачивается на угол я -р.

3) Точки, расположенные внутри многоугольника, образованного указанными прямыми, соответствуют точкам, лежащим в верхней половине плоскости С-

Так как разность 1 - а обращается в нуль при i=a, то производная dz/d в этой точке равна нулю или бесконечности (в соответствии с тем, будет ли а > я или а < я). Поэтому мы исключаем точки а, Ь, с, ... на действительной оси С. проводя около этих, точек, как из центров, полуокружности с малыми радиусами г, расположенные в верхней полуплоскости X,-

Полуокружность с центром в точке а пересекает действительную ось в точках Oj и Ог, как показано на рис. 176. Будем предполагать, что точка пробегает действительную ось в направлении возрастания величины (так что d -величина положительная). При этом точки а, Ь, с, ... обходятся по полуокружностям.

Пусть At, Ви Bt, Ci -точки плоскости г, соответствующие точкам о , bi, bt, Cj. Пусть К = Се*\ здесь С -действительная положительная константа, X - действительное число. Тогда, приравнивая аргументы в левой и правой частях вышеприведенного соотношения, получаем равенство

arg (dz) - arg (d5) = Я -ь - 1) arg (С - a) + -(--l)arg(£-6)+(-l)arg(C-c)+....

Когда точка С перемещается от точки at к точке 6 то arg (d) остается равным нулю; далее, arg (С -а) = О, так как величина (t - a) действительна и положительна; arg(S -6) = arg(t-с) = ... =я, так как все величины (С -Ь), (С -с), ... действительны и отрицательны.

Таким образом, имеем

arg(dz)=>. + (p-ff) + (Y-rt)-b... .

Это означает, что arg (dz) остается постоянным, пока точка £ движется от точки at к точке 6,. поэтому точка г описывает прямую линию AtBi. Такие же рассуждения показывают, что если величина 5 увеличивается от Ьг до с|, то

aгg(dz) = Л--(Y-я)-- ... .

При этом г описывает прямую линию BjCi. Кроме того, значение arg (dz) на прямой Л,в, превосходит значение arg (dz) на прямой Л,В| на

Отображение плоскости С на плоскость z, тределяемое соотношением

где множитель F не зависит от г и в. После интегрирования находим

г=г,-f-e*+ F; (2)

здесь г, - константа. Кроме того, так как угол р является положительным, то мы видим, что г-*2 когда г->0, поэтому точка z, соответствует точке В, в которой пересекаются линии Л^В, и В^С^.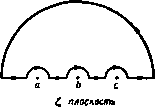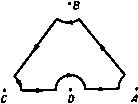

гпяоскостч Рис. 177.

Таким образом, точка г описывает многоугольник, вершины которого соответствуют точкам а, 6, с, .... а внутренние углы равны а, Р, у. соответственно. Кроме того, нз формулы (2) следует

arg(z-z.)=X-H-fargf.

Таким образом, когда точка описывает полуокружность, причем угол 9 уменьшается от я до О, то значение arg(z -Z) убывает на величину р и поэтому точка г опишет дугу окружности с центром в точке В, распаюжениую внутри многоугольника, если многоугольник простой. Таким образом, точки верхней половины плоскости С соответствуют внутренним точкам многоугольника. Итак, утверждение (3) доказано.

Остается рассмотреть, как замыкается многоугольник при изменении ве.1ичины С вдоль действительной оси от - аэ до + со. Для этого рассмотрим рис. 177, на котором показана действительная ось плоскости С с вырезами только в трех точках а, Ь, с, а также полуокружность большого радиуса с центром в начале координат. Когда точка С перемещается по действительной оси, обходя точки а, Ь, с по полуокружностям, то соответствующая точка плоскости z опишет стороны АВ и ВС треугольника ABC с вырезами в точках А, В к С.

величину (п -Р). Таким образом, направление движения точки г повернулось на угол (я -Р) в положительном направлении. Итак, утверждения (1) и (2) доказаны. Далее, на полуокружности имеем

Считая радиус г малым, с достаточной точностью можем записать соотношение

Когда а->-00, то JTa -1; тогда это уравнение принимает

внд

На большой полуокружности l = ReO; если радиус R достаточно велик, то мы можем с достаточной точностью заменить разности (С -о), Ц - Ь), Ц - с) величиной Re. Тогда из уравнения, определяющего преобразование, получаем соотношение, аналогичное формуле ( ).

Так как а + Р + у=я, то получим

отсюда, интегрируя, находим

2 = 21,--в <-в).

где 2 - константа, к которой стремится точка 2 при R-co. С другой стороны,

аге(2-2о) = я+Л-в.

Поэтому, когда точка £ описывает большую полуокружность, угол в изменяется от О до я, а значение arg(2 -z,) изменяется от я--А, до Л. Таким образом, точка г описывает полуокружность малого радиуса C/R с центром в точке D, как показано на рис. 177. Когда R->co, то полуокружность в плоскости 2 стягивается в точку. Мы видим опять, что область внутри треугольника с вырезами преобразуется на верхнюю половину плоскости С-Интегрируя уравнение преобразования, получаем

где /. - произвольная константа, от которой можно освободиться соответствующим выбором положения начала координат на плоскости z.

Изменение угла к приводит к изменению ориентации многоугольника, а изменение константы С изменяет масштаб. Отсюда следует, что все

многоугольники, соответствующие заданным значениям а. Ь, с.....

а, р, Y. . подобны между собой. В гидродинамических приложениях мы будем иметь дело только с простыми многоугольниками, обычно простира-юишмнся до бесконечности. Три величины а, Ь, с могут быть выбраны произвольно, но так, чтобы они соответствовали трем вершинам заданного многоугольника; остальные величины следует подобрать так, чтобы получился многоугольник правильного вида. Надлежащим подбором констант С и X устанавливаются затем масштаб и ориентация.

Если преобразование дает простой многоугольник, то отображение является конформным, так как в таком случае удовлетворяются условия (а) и (б) п. 5.62 для действительной оси с вырезами, которые можно сделать бесконечно малыми.

Наконец, остается рассмотреть случай, когда вершина многоугольника соответствует бесконечно удаленной точке действительной оси плоскости С-Если, например, точка а-* -оо, то, выбирая константу К, можно написать уравнение, определяющее преобразование, в форме

л В С Doo

г-плоскость пяоспость

Рис. 178.

S=-оо, 1= -I, 5=1 на действительной осн плоскости Если мы развернем границу полуполосы и расположим ее вдоль действительной оси плоскости С. то вершины Л и D перейдут в бесконечно удаленную точку плоскости

Таким образом, в соответствии с теоремой Шварца - Кристоффеля единственными внутренними углами при таком отображении будут углы В и С. равные п/2 каждый. Беря оси координат, как указано на рис. 178, получаем

f =К(£+1П(С-1Р=-.

отсюда имеем

Если положить Arch 1=0, то получим Archх = In(х + Ух-1), отсюда Arch(-1) = /я. Таким образом, 1=0, ai = K{ia), поэтому

z=ArchS или S = ch.

10.32. Отображение бесконечной полосы. Возьмем бесконечную полосу ЛооВооСсоОк, ширины а и предположим, что точки 5 и С , рассматриваемые как совпадающие, переходят при отображении в точку С = 0. Предположим также, что начало координат О переходит в точку 5 = 1. а точка F{z = ai) переходит в точку С=-1 (рис. 179). Тогда точка Отбудет, очевидно, соответствовать точке =со.

Угол в вершине БооСоо равен нулю, и поэтому получим

z=KlnZ + L.

Возьмем оси координат, как показано на рис. 179. Определим логарифм так, чтобы величина z обращалась в нуль при 5 = 1. Тогда получим

0=Klnl-t-L, ai = K\n{-\) + L. Таким образом, имеем L = 0, 1Кя = 1а. Поэтому

z=lnC, или 5 = е' / . (1)

Таким образом, множитель, соответствующий а=-оо, в уравнении пропадает и угол а в уравнение не входит.

10.31. Отображение полубесконечной полосы. Полубесконечную полосу AcoBCDao ширины а будем рассматривать как прямоугольник с двумя вершинами в бесконечности. Пусть точки Л , В, С преобразуются в точки

Соответствующие линии иа обеих плоскостях показаны на рис. 175 (X, X/). Прямые X = const преобразуются в окружности С = const, линии

const переходят в лучи arg С = const, выходящие из начала координат плоскости С- Если точки Аоо и £) переходят в точку С =0, то преобразование принимает вид

В некоторых случаях удобно располагать начало координат плоскости г в точке Е на средней линии полосы. Соответствующее преобразование

у у

Cm>/f }}}}}>}>}

г-плоскость

Г В.С О От пмкяоат

Рис. 179.

получается заменой величины z на величину z + ia/2 в формуле (I), так что в этом случае получим формулу

2 = -InC-, или =ie */.

10.40. Источник, расположенный в стенке канала (рис. 180). Пусть начало координат расположено в щели канала, а действительная ось поме-

ВС 1 0

С - плоскость

г-пмсщвсть

Рис. 180.

щена на одной стороне канала A oBaoCaoD , щирина которого равна а (рис. 180).

Пусть nm -объем жидкости, втекающей в канал в точке О в единицу времени через щель единичной длины. Таким образом, в точке О имеется источник мощности т. Условимся, что на бесконечно большом расстоянии от источника О поток в канале будет равномерным. Для этого в точках Л и £ , должны находиться стоки мощности /.

Будем считать точки В„, С совпадающими; развернув границу канала, совместим ее с действительной осью плоскости i так, чтобы точки В . С перешли в точку = 0.

Тогда по формуле Шварца -Кристоффеля (п. 10.32) получим

причем точка 2 = 0 соответствует точке £=1.

Таким образом, в плоскости С мы имеем сток мощности ЧгШ в точке J=0 и источник мощности m в точке С= 1- Этому течению соответствует

dw тп .1 яг

обращается в нуль в точке z = ai. Следова-тельно, давление на линии АоаВоо достигает максимума в точке Р, и поэтому в осталь- Рис. 181.

ных точках стенки оно будет меньше.

Таким образом, рассматриваемое движение жидкости оказывает воздействие на стенку в окрестности точки Р; при отсутствии упора стенка в этой точке выпучивается в наружную сторону. Скорость течения вдали от начала координат равна тп12а.

Кроме того, если линию тока ОР принять за твердую стенку, то получим течение в полубесконечном прямоугольном канале, вызванное источником, помещенным в одном его угле, как изображено на рнс. 181. Иначе говоря, мы имеем двумерный поток, образующийся при истечении жидкости из большого прямоугольного сосуда через небольшое отверстие в его угле.

10.50. Источник, расположенный посередине между двумя плоскостями.

Решение этой задачи можно получить, используя результаты п. 10.40 и применяя принцип отражения.

------------ф

Рис. 182.

Располагая оси координат, как указано на рис. 182, допустим, что в начале координат имеется источник мощности т, расположенный посередине между двумя плоскостями, расстояние между которыми равно 2а. Тогда

a;=-mlnshH. (1)

Эта функция удовлетворяет требуемым условиям в области между верхней стенкой и действительной осью и принимает действительные значения на действительной оси. Таким образом, условия п. 5.53 выполнены и функ-

следующий комплексный потенциал:

ш = - m In (5 -1)+у m 1п (С) = - m In (С'/, j-v,). Учитывая равенство

получаем комплексный потенциал в виде

ш= -m\nsh~.

Физически очевидно, что разветвляющаяся линия тока представляет собой прямую, выходящую из точки О и упирающуюся в противоположную стенку канала в точке P{z = ai), являющейся критической. Действительно, производная

пггтттттЬ

Ar)i,iiii )iirr.

z-ппоскость 1-ппоскость

P н с. 183.

Дно потока AcbBCD является простым многоугольником и, следовательно, может быть отображено на действительную ось плоскости причем так, чтобы точки В и С перешли соответственно в точки {; = -1 и С=1-Применяя преобразование Шварца -Кристоффеля, имеем

$ = /C(t+l)- (t-l)-- = AC=+i.

z=/C{/? + Arch;)-fL.

Так как функции V - 1 и Arch£ являются многозначными функциями, определим их в различных частях плоскости.

На рис. 184 изображена произвольная точка плоскости отстоящая на расстояниях л и соответственно от точек -f 1 и - 1. В этом случае имеем

;-1 = -,в 1, t-fl=r.e*4

здесь УТг обозначает арифметический Рис. 184. квадратный корень из произведения.

Для точек на действительной оси положим Z = l- Тогда если £ > 1, то мы должны положить в, = 0, в, = 0. Если - 1 < £ < 1, то О, =я, Ог =0, поэтому

VVl = 1/77, = i VTJf Кроме того, О, = я, Oj = я, когда 5 < - 1, в силу этого

VV\ = 1/77, = - ч7,.

АгсЬ;=1п(5-нК?).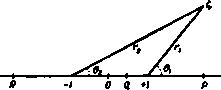

цию W можно аналитически продолжить ниже действительной оси, давая ей комплексно-сопряженные значения в комплексно-сопряженных точках, что вполне согласуется с формулой (1).

Можно также отметить, что формула (1) дает комплексный потенциал бесконечной последовательности источников, расположенных вдоль оси у на расстояниях 2а между собой, так как имеем

sh=0 при z = 0, ±2ai, ± 4at, ± 6а/.....

10.60. Бесконечно глубокий поток с уступом на дне. Пусть имеется вертикальный уступ ВС на горизонтальном дне потока, скорость которого в бесконечности равна U (рис. 183).

и

\Зя/2

Поэтому мы получаем

= {-y{V-\) + ln[-l+V(V)]+in}K+L на линии Л В(£<-1),

z = {iy(1-1*)+\п[l + iY(lZr)]}K+L на линии ВС,

z=[y(V-\)+\n[l+y(5 -\)]]K+L на линии CD .

Если мы положим z=0 в точке С, а также z = ih в точке В, то получим L = 0, ih = inK, так что K = h/n и поэтому

г={/(С^) + АгсЬС).

Теперь рассмотрим комплексный потенциал. Равномерный поток в плоскости Z можно получить, поместив источник в точке D и одинаковый по мощности сток в точке Л . Таким образом, в плоскости 5 мы должны также иметь источник и сток в соответствующих точках, так что в этой плоскости также будет равномерный поток, скорость которого пусть будет V. Следовательно, w = V, поэтому

dz К V t+\

dz ~ dz~ К V l+\ Но в бесконечно удаленной точке имеем

dwldz = U, 1=оо. Отсюда и = VlK = Vnlh. Таким образом.

Заметим, что в точке В скорость равна бесконечности, а в точке С равна нулю. Более удобная форма решения получится, если положить { = ch/. Тогда имеем

я я и

Принцип отражения позволяет .....................Г

нам применить тот же комплек-

Рнс. 185.

сный потенциал к потоку бесконечной ширины, обтекающему полубесконечное цилиндрическое тело прямоугольного сечения, изображенное на рис. 185; при этом начало координат расположено в точке С, а действительная ось направлена против течения.

Читатель может убедиться, интегрируя выражение ViW вдоль линии ев, что сила, приходящаяся на единицу длины линии ВВ, является конечной величиной.

10.70. Канал с резко изменяющейся шириной. Рассмотрим изображенный на рис. 186 канал с параллельными стенками и с шириной, резко меняющейся от величины h до величины k.

Если скорость в точке Л равна U, то в силу уравнения неразрывности скорость в точке В равна Uh/k.

Развернем граничную ломаную AcoB >CaoDEF иа действительную ось плоскости С, считая, что точки 5 и С совпадают и переходят в точку

Пусть точке D соответствует точка 5 = 1 и точке Е пусть соответствует точка С = а; действительное число а мы определим далее; этому числу нельзя давать произвольное значение, так как значения соответствующие точками fioD. Cod и D, уже были выбраны.

В вершине BojCm многоугольника угол равен нулю, поэтому преобразование Шварца-Кристоффеля имеет вид

= АСГ -1)*/ (£-а)-*/ .

Далее, поток в плоскости г вытекает из источника мощности Uh в точке Ло. и втекает в сток мощности Uh в точке Boo. Следовательно,

Boo U(i(t<(l

Coo тттптт

i((i(t<a<ii(((ii(t((((t((t

41})) t)) и).

и

ft)))iifinii>nii Fm

2- плоскость

I a

>))>>} t n}TW)> >))))f})>)}f)f inn I}))),

тттттгт-п

Лот

В.С D £ -плоскость

Ряс. 186.

в плоскости мы имеем в начале координат сток, который поглощает в единицу времени объем Uh, приходящийся на угол п. Поэтому мощность стока равна Uh/n, следовательно.

так что = . Отсюда в силу формулы (1) имеем

dw Uh ,/С-а

Далее, в точке Лоо(С=оо) получаем, что = U, если действительная ось параллельна прямой АооВоо. Поэтсшу

Uh ПК

Кроме того, в точке flao(S = 0) находим, что =- Поэтому

Uh Uh

так что

Для получения явной зависимости между величинами z и w следует проинтегрировать соотношение (1).