Когда Y =const, относительные траектории являются эллипсами

x* и*

-,Н-г=const,

которые подобны контуру поперечного сечения цилиндра. Для относительной скорости мы имеем уравнения

dx да 2а < у

--а*+* dt

26 <ox

Рассмотрим частицу, которая в момент времени / = 0 находится в точке (ka, 0) на главной оси. Тогда в момент времени t координаты этой точки равны

x = ftacosQ/, y=-kbsmQt, Q= a*-\-b*

Таким образом, в момент времени / частица находится в точке эллипса, эксцентрический угол которой равен -Qt. Это относится к движущимся осям. Если рассматривать движение в неподвижных осях, то частица будет иметь угловую скорость дрейфа, равную <u - Q = {a-b)*<u/{a*+b*), наложенную на ее колебательное движение.

Предположим, например, что в начальный момент времени положительная половина главной оси эллипса отмечена краской. Эта линия будет оставаться радиусом эллипса и периодически будет снова совпадать с главной осью. Если цилиндр совершает число полных оборотов, равное (а*4-6*)/(а-fe)*, то главная ось совершит полный оборот. Тем не менее движение остается безвихревым.

9.72. Вращающаяся равносторонняя призма, содержащая жидкость. Прямые

х - а = 0, x - yV+2a = 0, х + уУЗ + 2а = 0

образуют равносторонний треугольник ABC, центр тяжести которого нахо-дитсяв начале координат (рис. 171). Длина стороны треугольника равна 2a/V 3. Комбинируя эти уравнения в одно, мы получим уравнение границы в виде

F (X, у) = х'- Зху* + За (х* + у*) - 4а = О, или

-{г' + ?)+Загг-4а' = 0.

Сравнивая последнее выражение с формулой (1) п. 9.70, мы находим

f / . 1 г , 2а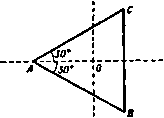

отсюда сразу получаем

65

Рис. 171.

Добавляя в функцию тока член ф= - у (о (х*-- / ), мы найдем уравнение линий тока в относительном движении F (х, у) = const, или

(х-а)(х-уУЪ + 2а) (х+ уУЪ-\-2а) = с .

где с-некоторая постоянная. Это уравнение определяет кубические кривые, имеющие стороны нашего треугольника в качестве асимптот, а петли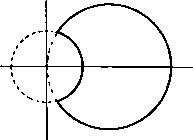

гг = а(г + г) + Ь^-аЬ*(- + 1) ,

Р - а; = ш(аг-

Заметим, что особая точка г = 0 находится вне контура поперечного сечения цилиндра.

9.74. Метод конформного отображения для комплексного потенциала.

Пусть кривая С является контуром поперечного сечения цилиндра, содержащего жидкость и вращающегося с угловой скоростью ш вокруг точки О, лежащей внутри поперечного сечения. Предположим, что внутренняя область, ограниченная этой кривой, может быть конформно отображена на внутренность единичного круга в плоскости J с помощью функции

г = (1)

Тогда мы можем, согласно формуле (7) п. 9.63, получить комплексный потенциал в виде

w = B,{l). (2)

Так как разложение этой функции в ряд содержит только положительные степени С. то мы получим конечные скорости в начале координат и вообще в любой точке области течения. В самом деле,

а это выражение не может обращаться в бесконечность, потому что функция / (С) не имеет нулей в области, занятой движущейся жидкостью.

9.75. Криволинейная многоугольная граница. Преобразование

г = с1{1 + т. (1)

где с и л -некоторые действительные положительные постоянные, конформно отображает внутренность единичной окружности в плоскости С на внутренность правильного криволинейного многоугольника ), имеющего п сторон. Преобразование является конформным во всех точках внутри единичной окружности, если функция / (С) не обращается в нуль или беско-

1) Кривая, ограничивающая этот многоугольник, называется эпитрохоидой.

кривых, ограниченные этими асимптотами, находятся внутри треугольника ЛВС. В частности, если с = 0, то ломаная линия ABC является относительной линией тока.

9.73. Круговой цилиндр с вырезом. Пусть поперечное сечение цилиндра имеет форму лунки, ограниченной окружностями

х*+у*-Ь* = 0, х* + у*-2ах = 0,

как показано на рис. 172. Жидкость находится внутри цилиндра. Центр первой окружности лежит иа второй окружности.

Перемножая последние два уравнения, мы получаем

нечность в единичном круге. Это имеет место, если выполнено условие

0<Я(л--1)<1. (2)

Теперь положим 5 = в*ч и 2 = re**; тогда легко получить соотношения

г = 22 = с (1+Я,*+ 2Я, cos пл), (3)

. д sin+>-sln(n+i)n /4\

К - cosf4-Xcos(n--l)ti

Отсюда следует, что на граничной кривой С величина г принимает экстремальные значения в том случае, когда sinnn=.0, т. е. когда

t = e = s4. s = 0, 1, 2, .... 2п-1. Таким образом,

Кривая С имеет п осей симметрии, если п -нечетное число, и 2п осей симметрии, если п -четное число. В случае п -1 простым переносом начала координат по формуле г' = г + кс =г'е* можно убедиться, что кривая С является эллиптической улиткой

r=a+&cose, &<а а-с, = 2Я.) . (5)

Для заполненного жидкостью вращающегося цилиндра, поперечное сечение которого задается формулами (3) и (4), граничная функция имеет вид

В (S) = /ас {1 + Х + X (S -1- Г )}, следовательно, формула (2) п. 9.74 дает

wtwcXC . (6)

Для кинетической энергии жидкости мы имеем выражение

Г = /с^ wdw = iQ\ t©c XS (m<oc XC- - dt),

(с) (с)

или

9.76. Вращение вокруг эксцентрической точки. Если ось вращения проходит через точку Zq, а не через начало координат, то начало координат можно выбрать в качестве полюса и движение будет эквивалентно вращению вокруг начала координат с угловой скоростью ш и поступательному движению вместе с началом координат с комплексной скоростью 2о©. Новые граничные условия (п. 9.40) тогда удовлетворяются комплексным потенциалом

w-i(oZoZ,

где W -комплексный потенциал, когда вращение происходит вокруг начала координат.

где k = Vcei\\\. Пользуясь этими формулами, нарисовать кривые 9=coiut, ф=сопз1.

5. Очень длинная тонкая твердая доска шириной 2с, плавающая по поверхности глубокой воды, получает удар, направленный вертикально вивз, импульс которого равен /. Удар при.10жеи в центре доски. Показать, что скорость воды, иаправленная вверх, иа расстоянии X от оси доски равна

{явК**-с }{х-Ь

где Q -плотность воды.

е. К погруженному в жидкость эллиптическому цилиндру, масса которого равна М, а полуоси равны а и 6, пркложен импульс сил. Показать, что начальное движение цилиндра задается формулами

н(А1--яв* ) = /, о(А --ява )-У, л А!* +у яв(а -6 ) J =С,

где /, У, С-компоненты импульса.

7. Эллиптический цилиндр, полуоси поперечного сечения которого равны ашЬ, вращается вокруг своей оси с угловой скоростью ш. Цилиндр находится в жидкости, которая покоится на бесконечности. Найти потенциал скорости и функцию тока движущейся жидкости и вычислить кинетическую энергию единичного слоя жидкости. Кроме того, иайти точки иа границе цилиндра, в которых скорость жидкости достигает максимальной и минимальной величины. Показать, что в этих точках давление принимает соответственно минимальное н максимальное значенве.

8. Пусть бесконечно длинный цилиндр плотности о, поперечное сечение которого представ.1яет собой эллипс с полуосями а л Ь, вращается вокруг своей продольной оси в безграничной жидкости плотности q. Показать, что при этом квадрат радиуса инерции цилиндра относительно оси вращения эффективно возрастает иа величину

g (ai-fci)t 8а ab

Бесконечная плоская пластинка шириной 2t вращается с угловой скоростью ш в жидкости плотности ц. Покаээть, что момент силы (приходящийся на единкцу толщины), необходимый для поддержания вращения пластинки, равен

1 ,.<fm

ПРИМЕРЫ К ГЛАВЕ 9

1. КруговоА цилиндр риднуса а движется со скоростью U перпендикулярно своей оси в безграничной иесжиыаемоа жидкости плотности q. На цилиндр наложена циркуляция /. Показать, что если ( , d)-компоненты скорости точки z=x-\-iy, то

Пусть цилиндр вращается с угловой скоростью , а циркуляция / выбрана так, чтобы сделать среднюю квадратичную скорость жидкости на границе цилиндра минимальной. Доказать, что в этом случае / = 2яа*ш, и вычислить силу, действующую со стороны жидкости на цилиндр.

2. Пусть жидкость, обтекающая неподвижный круговой диск, имеет скорость на бесконечности, равную V. Найти распределение скорости. Показать, что максимальная скорость в жидкости равна 2V. Показать также, что если цилиндр движется поступательно в покоящейся жидкости, то скорость жидкости изменяется обратно пропорционально квадрату расстояния от центра сечения цилиндра.

3. Если вся граница области, занятой жидкостью, покоится, то ие может существовать чисто безвихревого движения жидкости. Доказать эту теорему, введя и объяснив необходимое ограничение иа вид области.

Пусть пространство между двумя неподвижными коаксиальными цилиндрами радиусов а н 6 и двумя плоскостями, перпендикулярными к оси цилиндров и отстоящими друг от друга на величину с, занято жидкостью плотности q. Найти потенциал скорости движения, кинетическая энергия которого равна Т.

4. Пусть <р и ф -потеициал скорости и функция тока для эллиптического цилиидра, движущегося поступательно в направлении большой оси. Показать, что

\ a*+b

13. Эллиптический цилиндр, полуоси которого равны а и 6, заполнен несжимаемой жидкостью. Цилиндр вращается вокруг своей продольной оси с угловой скоростью ш. Показать, что компоненты скорости (и, v), параллельные осям Ох и Оу эллипса, задаются формулами

а*-6 а -6

Показать, что координаты X и У (относительно неподвижных осей в точке О) произ* вольной частицы жидкости в момент времени ( выражаются формулами

... [ <]+ [ <]},

где X-некоторая постоянная, зависящая от частицы жидкости. В момент / = 0 частица находится иа оси ОХ.

14. Тонкая оболочка в форме эллиптического цилиндра, оси поперечного сечения которого равны 2а и 26, вращается вокруг своей оси в покоящейся жидкости. Оболочка заполнена жидкостью той же плотности. Показать, что отношение кинетической энергии жидкости внутри цилиндра и кинетической энергии жидкости вне цилиндра равно 2a6/(a +62).

15. Эллипс

а{х*-у*)+2Ьху-,л(х*+у*)+с=0,

заполненный жидкостью, вращается вокруг начала координат с угловой скоростью ш. Показать, что функция тока движения жидкости имеет вид

1=а{х*-у*)+2Ьху.

16. Пусть функция тока задана в виде ф = С (дс -Зху ). Подобрать постоянную С так, чтобы функция тока описывала движение жидкости во вращающейся призме, стороны которой заданы уравнениями

дс = а, х+2а = ±У1у.

Показать, что время, необходимое частице, чтобы продвинуться нз начала стороны поперечного сечения до середины той же стороны, равно 1пЗ/(в|3.

Вычислить эффективный раднус инерции призмы относительно оси вращения.

17. Цилиндрический сосуд, поперечное сечение которого является сегментом параболы 2(х* -Зу*}-\-х-\-ау=0, отсекаемым осью х=0, заполнен жидкостью и вращается с по-чтояиной угловой скоростью, равной единице, вокруг осн, проходящей через начало к(Н)рдинат и параллельной образующей цилиндра. Доказать, что функция тока течения имеет вид

-ф = 2 (х -Здс1/*) + 1 (x -y )-f одсу.

10. Пустотелый цилиндр, ограниченный эллипсом Ь*х*-\-а*у*=аЧ*, содержит в себе жидкость и вращается с угловой скоростью ш вокруг своей продольной осн. Показать, что функция тока движения жидкости имеет вид

Доказать, что частицы жидкости пробегают эллипс одни раз за время

11. Жидкость плотности Q полностью заполняет сосуд в форме длинного эллиптического цилиндра; полуоси поперечного сечения цилиндра равны а и Ь; массой цилиндра можно пренебречь. Цилиндр вращается вокруг своей оси с угловой скоростью ш. Вычислить кинетическую энергию жидкости на единицу длины цилиндра и выразить ее через эффективный момент инерции цилиндра.

12. Эллиптический цилиндр, содержащий жидкость, вращается вокруг своей продольной оси. Доказать, что отношение кинетической энергии жидкости в данном движении и кинетической энергии той же жидкости, движущейся как твердое тело, равно

Q -плотность жидкости.

Доказать, что для эллиптического цилиидра, вращающегося вокруг фокуса, имеет место соотношение

яв*(а -6 ) (5в -Ь36 )

1-1 =

4(а -Ь6 )

20. Цилиндрический сосуд, заполненный несжимаемой жидкостью плотности q, вращается с угловой скоростью ш вокруг некоторой оси, параллельной образующей. Пусть поперечное сечение сосуда ограничено окружностью радиуса а, центр которой О лежит на оси вращения, и радиусами в=±а. Показать, что в этом случае функция тока имеет вид

<2и+1)я

1 со52в coi (2 -И)яе

-(2п--Оя[(2 -1-1) я .-16а -

Вычислить кинетическую энергию слоя жидкости единичной толщины.

21. Прямоугольная призма, стороны поперечного сечения которой равны 2а и 26, вращается с угловой скоростью Q вокруг своей оси Ог. Призма содержит несжимаемую .жидкость плоскости Q, которая совершает безвихревое движение. Показать, что с точностью до несущественной постоянной функция тока течения имеет внд

J16Q -о (-1) я 2л (2n-fl)

=0

а. со. <?i±i>i-f

ct, (2 -f 1)я6 2a

,(2л-Н.1)яа -26-

26

Найти выражение для потенциала скорости q> и вывести выражение для кинетической энергии жидкости, приходящейся на единицу длины призмы.

22. Твердый цилиндр движется в жидкости перпендикулярно своей образующей. Задана линейная скорость Q=t/-frt центра тяжести сечения цилиидра относительно осей, связанных с сечением, и угловая скорость . Доказать, что иа границе цилиидра функция тока с точностью до постоянной величины имеет вид

где черта над буквой обозначает комплексно-сопряженную функцию.

18. Уравнение

х<-6* j, -f y -f 2а (* -!--в<=О

приводится к виду

[(/2+1) х -(К2-1) 1, -а ] 1(2-1) x*-(V-\-\) = 0.

Цилиндр, поперечное сечение которого ограничено этими двумя параболами, вращается вокруг начала координат с угловой скоростью ш. Доказать, что функция тока движения жидкости внутри цилиидра задается формулой

---4Р--

IV. Полый цилиндр с поперечным сечением 5 наполнен невязкой жидкостью и вращается с угловой скоростью ш вокруг оси, параллельной его образующей. Показать, что если функция X удовлетворяет уравнению V*x= - внутри поперечного сечения цилиидра и обращается в нуль на его гр>ииие, то кинетическая энергия Т и момент количества движения G относительно оси вращения на единицу длины цилиидра задаются формулами

2Г=в (/-У), 0=0© (/-У),

где /-момент инерции поперечного сечения относительно оси вращения, У = 4 iXdS,

Примеры 2S1

Жидкость заключена между двумя цилиндрами, движение которых определено, как и выше, величинами Q, а и Q, а'. Доказать, что количество движения жидкости равно AtCy-MQ, где М' и уИ-массы жидкости (приходящиеся на единицу толщины), которые могли бы содержать соответственно внешний и внутренний цилиндры.

23. Круговой цилиндр, содержащий невязкую несжимаемую жидкость, приводится во вращение с постоянно возрастающей угловой скоростью вокруг вксцентрнческой оси, параллельной оси цилиндра. Найти движение жидкости.

Найти также движ1еиие жидкости, если цилиндр твердый и окружен бесконечной массой жидкости. Рассмотреть два случая: а) первоначально циркуляция вокруг цилиндра отсутствует; б) в начальный момент времени вокруг цилиндра существует циркуляция янтенсивности /.

24. Найти линии тока двумерного течения жидкости, заданного комплексным потенциалом

9+f*=-5

Показать или проверить, что траектории частиц жидкости (в полярных координатах) могут быть получены исключением I из равенств

г cos (я/--в)-хв= rsin (п1+в)-уо=п1 (Хо-Уо).

25. Жидкость содержится между эллиптическими цилиндрами

где а, b и к-некоторые постоянные, и вся система вращается вокруг осн Ог с угловой скоростью Q. Показать, что потенциал скороств ф, отнесенный к осям Ох и Оу, задается формулой

и что поверхности равного давления являются гиперболическими цилиндрами

х g

3ai+6t в --36

const.

Определить также кинетическую энергию и момент количества движения относительно оси Ог.

26. Невязкая несжимаемая жидкость постоянной плотности q совершает двумерное безвихревое движение между двумя цилиндрами, поперечное сечение которых ограничено кривыми Ci и Сг, причем кривая Ci полностью лежит внутри кривой Сг. Доказать равенство

(Ci) (C,) (Ci) (Ct)

где ф-потенциал скорости, предполагаемый однозначной функцией, /-косинус угла между внешней нормалью и осью х, дифференцирование производится вдоль внешней нормали.

Бесконечный твердый цилиндр, поперечное сечение которого ограничено кривой С, движется в жидкости вдбль оси х со скоростью и. Пусть для больших значений г комплексный потенциал задается формулой

где X и ц действительны, а г=х-\-1у. Докавать, что кинетическая энергия жидкости, приходящаяся иа единицу длины, равна

1вУ (2лХ-А),

где i4 -площадь, ограниченная кривой С.

i) Знак О читается как свеличина порядка и означает, что существуют такие положительные числа К, R, что абсолютное значение рассматриваемой величины меньше чем К/г* при условии, что г|=г>/?.

Пусть бесконечный прямой цилиндр, поперечное сечение которого ограничено кривой Г1Г2=6*, где Tj и Г2-расстояния от двух точек Р Q, удаленных друг от друга на расстояние 2а (Ь> а), движется со скоростью U вдоль прямой PQ в жидкости, покоящейся иа бесконечности. Показать, что кинетическая анергия жидкости, приходящаяся на единицу длины, равна

где

£(ft)=V (1-ft sin x)*/ dx.

о

27. Два концентрических цилиндра, радиусы которых равны а к Ь, движутся со скоростями и V вдоль линии, соединяющей их центры. Доказать равенство

Ua*-Vb* , , аЧ* cos в

Доказать также, что когда скорость V направлена перпендикулярно скорости U, то имеет место равенство

bW / , а*\ . , аЧ) / , 6 Л о

причем в обоих случаях через а обозначен радиус внутреннего цилиндра.

28. Пространство между двумя коаксиальными цилиндрическими оболочками радиусов а и 6 заполнено жидкостью плотности q. Внешняя оболочка радиуса а внезапно приводится в движение со скоростью U.

Показать, что импульс сил, приходящихся на единицу длины оболочки, который необходимо приложить к внутреннему цилиндру, чтобы удержать его в покое, равен

2яса 6 6/

Показать также, что импульс сил, который необходим, чтобы привести в движение со скоростью V внутренний цилиндр, когда внешний цилиндр покоится, равен

{(о+в) а - (о - в) * } и,

где а-плотность цилиндра.

29. Два круговых цилиидра радиусов ana движутся со скоростями I и V в направлении, перпендикулярном прямой, соединяющей их центры. Определить приближенно потенциал скорости течения жидкости. Вывести также потенциал скорости в спучае, когда эти цилиндры неподвижны и обтекаются потоком, перпендикулярным прямой, соединяющей их центры.

Пусть 1-скорость равномерного потока, обтекающего два неподвижных цилиндра в направлении, перпендикулярном прямой, соединяющей их центры. Радиус каждого цилиидра равен а, а расстояние между центрами равно с.

Показать, что если отношение с/а ие мало, то среднее значение скорости иа прямой, соединяющей ближайшие точки цилиндров, равно приблизительно

yi±a с-а

Глава 10 ТЕОРЕМА ШВАРЦА - КРИСТОФФЕЛЯ

10.10. Простые замкнутые многоугольники. Примерами обычных многоугольников являются, скажем, прямоугольник или правильный шестиугольник. Для гидродинамических приложений необходимо расширить это понятие до прямолинейных конфигураций, которые на первый взгляд ничего общего не имеют с многоугольниками элементарной геометрии. Рассмотрим два свойства прямоугольника (или правильного шестиугольника).

а) Можно перейти от одной определенной точки границы к другой определенной точке границы, следуя по пути, который никогда не покидает границу. Граница является связной.

б) Граница области делит точки плоскости на два типа: одни точки можно назвать внутренними, а другие внешними. Внутренними точками являются такие точки, что любые две из них можно соединить линией, нигде не пересекающей границу. То же справедливо для внешних точек. С другой стороны, невозможно перейти от внутренней точки к внешней, не пересекая где-либо границу.

Любая конфигурация прямых линий в плоскости, которая обладает свойствами (а) и (б), называется простым замкнутым многоугольником. Термин простой означает, что каждая точка плоскости является либо внутренней точкой, либо точкой границы, либо внешней точкой, причем точки каждого класса образуют связную систему.

Во многих важных гидродинамических задачах гра1п<цы многоугольника простираются до бесконечности.

Мы будем рассматривать в качестве внутренних точек многоугольника (см. п. 5.70 такие точки, которые находятся в области, расположенной слева от наблюдателя, описывающего границу в заданном направлении. Некоторые из таких многоугольников изображены на рис. 173. Точки, удаленные на бесконечно бшьшое расстояние, отмечены индексом оо; внешние области многоугольников заштрихованы. В каждом случае буква Р обозначает внутреннюю точку.

На рис. 173 (/) показан прямоугольник с двумя вершинами в бесконечности. Этот прямоугольник можно было бы рассматривать как треугольник с одной вершиной в бесконечности (соответствующей точкам А^, и О ). На рис. 173 ( ) все вершины четырехугольника ABCD находятся в бесконечности.

На рнс. 173 ( /), {IV) показан треугольник с двумя вершинами в беско-нечм<х:тп, причем внутренней областью считается внутренняя или внешняя сторона треугольника АоеВСх, в соответствии с направлением обхода границы. Диаграмму на рис. 173 {V) можно рассматривать как прямоугольник, в котором две вершины совпадают в точке В, С, а другие две совпадают в бесконечности. Эту диаграмму можно рассматривать как полубесконечную прямую линию, описываемую дважды в указанных направлениях. Этот пример имеет много приложений; мы отметим лишь ту особенность, что данный прямоугольник не содержит внешних точек. Все точки плоскости принадлежат либо границе, либо внутренней области в соответствии с нашим определением внутренней области. Для более глубокого понимания рассмотренного примера

BHiiiiiimiiifjmiimiiiiii

Р

inimiifiiiiu((i(tuii(ii4(ii(((niii((tд

СтлилипипииптПитттппипт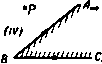

Рис. 173.

стороны действительной оси плоскости t; течение жидкости внутри многоугольника преобразуется в течение иа полуплоскости

Допустим, что такое отображение осуществлено; тогда ясно, что вершины углов многоугольника перейдут в точки действительной оси плоскости С-

В С ft.

Am. В Cm

(IX) /7/J /W/Wf->/W.>WJM.W./J.f.>

Рис. 174.

Это отображение можно интуитивно рассматривать как развертывание многоугольника до тех пор, пока его граница не перейдет в бесконечную прямую линию; при этом произойдут локальные изменения размеров, необходимые для соблюдения конформности отображения.

Если многоугольники, изображенные на рис. 173 (/-VI), отобразить указанным путем, то в результате мы получим полуплоскости, изображенные на рис. 174 {VII-IX). В случае, изображенном на рис. 174 ( ), можно считать, что точки Boo и Соо переходят или в одну конечную точку В, С, или в две

на рис. 173 (V7) показана та же диаграмма в виде двух линий, причем считается, что прямые линии А^оВ и DooB не совпадают.

Теперь покажем, что граница любого простого замкнутого многоугольника на плоскости г может быть преобразована в действительную ось плоскости J с помощью конформного отображения; при этом внутренним точкам многоугольника будут соответствовать точки, расположенные только с одной