9.40. Функция тока на границе. Рассмотрим осн координат, связанные с цилиндром, который вращается и совершает поступательное движение.

Пусть и и V-компоненты скорости начала системы координат О, а ш-угловая скорость системы координат. Тогда компоненты скорости точки Р{х,у) границы цилиндра равняются и - уи, V+xut. Проектируя скорость на направление внешней нормали к границе в точке Р, мы получаем выражение

(U-yai)smQ-{V+хю) cos О,

где 6-угол наклона касательной к осн х.

Далее, sind = dy/ds, cos в =dy/ds, а нормальная скорость жидкости равна-дф/ds (рис. 168). Выписывая выражение для нормальной скорости, мы получаем

-=(и-уа,)-(У+х.).

Интегрируя это равенство вдоль границы, находим

= Кх - C/j, -f -i (О (х + i, ) -f В.

где В - произвольная постоянная. Таким образом, мы нашли значение функции тока на границе. Мы теперь видим, что с точностью до аддитивной постоянной функция тока ф является мнимой частью функции

f (г, i) =-((/- /V) 2 -Ь1 iW. (1)

Если мы обозначим U, V соответственно через f cos о н С sin а, так что полная скорость будет равна U и направлена под углом а к оси Ох, то мы получим равенство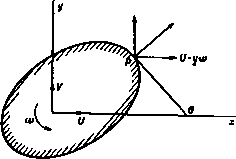

Рис. 168.

- Uze-< + ~iшz.

Функция, сопряженная с функцией / (г, г), равна

7(Z,Z):

-Uze+<-Y<лzz.

Так как ф является мнимой частью равенства (2), то - ф является мнимой частью равенства (3). Следовательно, вычитая из равенства (2) равенство (3), получаем выражение для функции тока на границе в виде

2ф = - f/ze-**+Uze>+imz.

9.50. Сила, действующая на движущийся цилиндр. В п. 6.41 мы получили выражение для воздействия жидкости на элемент ds границы цилиндра

dX - idy=- ipdz, dM + idN = pzdz. Далее, пусть dz = ds тогда dz= dze-*<. Следовательно,

:-iY=-i\ pe-idz, M + iN=\ pze-dz,

(C) (C)

где интегралы берутся по контуру С поперечного сечения цилиндра. Теперь, если скорость начала координат по отношению к осям, связанным с цилиндром, обозначить через W=U + iV, а угловую скорость -через и, то урав-

-у q J ( + 1Ш) {W-ш7) dl- in J dz,

С) (С)

M + iN-\fi\ zC + W-i<i>iydz +

+ ув$ z(W + ifz)(W-iaz)dz+ii \ zdl.

(С) (С)

Эти равенства являются обобщением теоремы Чаплыгина-Блазиуса; в случае установившегося движения жидкости относительно покоящегося цилиндра отсюда получается обычная теорема. Полученные выражения являются довольно громоздкими. Их можно легко упростить, если использовать комплексную форму теоремы Стокса (п. 5.43), согласно которой имеют место равенства

5 (W-icaz)4z = 2/ J - 2i(o (Г- icoz) dS = 4саА {W-ical), (5)

(С) )

где i4-площадь, ограниченная контуром, а Ze = Xe +<е~ положение центра тяжести этой площади. Кроме того, справедливы следующие равенства:

\ (W + шг) (W-i<uz)dz= -2i J ш (W- *<вг)dS = 2<йА (Г-laFe), (6)

(С) (S)

jj (-Wz-\-Wz + i<iizi)dz = -2/ jj (-P-f /(az)dS = 2iA (W- iaz). (7)

(c) (S)

9.52. Обобщение теоремы Чаплыгина-Блазиуса. Формула (3) п. 9.50 дает силу, действующую на движущийся цилиндр. Она может быть записана в виде

+у в J (W-iial)dz-jiQ J (W+iinz) (W-im)dI-iQ (pdz.

некие для давления запишется в виде (п. 9.30)

-f-i<ii + i{W + im)-i). (2)

где относительная скорость. Далее, на границе цилиндра жидкость движется по касательной к поверхности цилиндра, и. следовательно, комплексная скорость такого относительного движения равна

Из левой части равенства видно, что вектор относительной скорости касается цилиндра. В правой части равенства дана относительная скорость, представленная в виде суммы соответствукмцих слагаемых.

Подставим выражение для скорости qr из последнего равенства в формулу (2), а потом подставим выражение для давления р в формулу (1). Кроме того, учтем, что в точках на поверхности цилиндра выполняется равенство dz = e-dz. Таким путем мы получим следующие формулы для силы и момента, действующих на цилиндр:

где интегралы берутся вдоль контура цилиндра. Используя формулы (5) и (6) предыдущего пункта, мы получаем

Ч- 2i{jU)A {W-iioz) -1 Qco Л (T - iaz) - в J Ф d. (1)

Далее, dw равен приращению величины w при обходе цилиндра н,

следовательно, равен -2ях, где х-интенсивность циркуляции (которая Может быть равна нулю).

Кроме того, очевидно, имеет место равенство zda>= J z(dw + 2idyp),

поэтому, интегрируя по частям, находим, что

р^ф=1)-}фйг.

Так как произведение гф не изменяется прн обходе контура цилиндра, то 12ф1- = 0 и, следовательно,

zdw= zdw - 2i фйг.

Далее, нз формулы (4) п. 9.40 на поверхности цилиндра мы имеем 2/ф =: -Wz + Wz-t iiozz. Следовательно, нз формулы (7) п. 9.50 получим

rpdz=A(W-ifuZc). (2)

г = J zrfay - 2iA (W - iioz). (3)

Кроме того, на основании формулы (2), находим

J Фrfz = J (ш + /ф)dz=wdz + Ai (Г-ш'г^). (4)

Подставляя формулы (3) и (4) в формулу (1), мы получаем

Х-1У = -i.e 5 (-g-ydz-foH) \ idw-iQ\ wdz-

-2яхв1р-/сЛ {©(r-tW,) -fi (ir- )}

Это соотношение можно рассматривать как обобщенную форму теоремы Чаплыгина-Блазиуса для силы, действующей на движущийся цилиндр. Преимущество этой формы теоремы состоит в том, что все интегралы берутся по контуру цилиндра или по любому большему контуру, который стягивается к нему, не пересекая особенностей, таких, как источники, стоки или вихри.

Аналогичными вычислениями можно показать, что момент сил давления относительно начала координат является действительной частью выражения

-ув \ z()*dz-er 5 zdw + ii>fiAWz,V

+ \zwdz-A{2iz. + 2k), (6)

где * -радиус инерции сечения цилиндра относительно точки О.

Приведение формулы (4) п. 9.50 к предыдущему выражению с помощыо результатов п. 5.43 оставляем читателю в качестве упражнения.

Легко видеть, что начало координат удобно брать в центре тяжести сечения цилиндра, так как в таком случае 2=0.

Полученные результаты интересны тем, что они являются совершенно общими, так как могут быть применены как к установившемуся, так и к неустановившемуся движению.

В случае установившегося движения члены, содержащие производные по времени, исчезают.

9.53. Цилиндр, движущийся в безграничной жидкости. Если цилиндр движется в безграничной жидкости, которая покоится на бесконечности, то возмущения вследствие движения цилиндра должны исчезать на большом расстоянии от цилиндра. Таким образом, для больших значений z мы должны иметь dw/dz = 0.

Наиболее общий вид функции w, удовлетворяющей этому условию и условию непрерывности движения жидкости и потенциала, для больших значений z дается формулой

ш = 1х1пг+ ;++... , (1)

где x -интенсивность циркуляции. Тогда

dw 0 2ог

(2)

Kdz J ~ 3* г

Отсюда следует, что первый интеграл в формуле Чаплыгина - Блазиуса (5) п. 9.52 равен нулю.

Изменим везде знак перед величиной / и выберем начало координат в центре тяжести сечения, тогда мы получим следующее выражение для силы:

Х4- Г=<ов J zdw + iQ-§ J wdz+2axQlW+iQA ( И^--) (3) Из формулы (2), применив теорему о вычетах, получим Jzda>= J (/X-ii -...<fc= -2nia,. Кроме того,

wdz = tx z In zj + 2niai,

где Izinz] представляет собой приращение функции zlnz при однократном обходе контура. Если циркуляция остается постоянной, то частная производная от этого выражения по времени t равна нулю. Тогда из формулы (3) мы получаем

X + Т = - 2яс©Ш| + 2ayQiW + iqA (atW-i - 2nQ . (4)

Эта формула очень удобна тем, что не содержит интегралов. Пусть Oi-a + ib в выражении для комплексного потенциала (1). Тогда, вспоминая, что W=U + iV, где U, V-компоненты скорости начала координат, мы придем к следующим формулам:

X = 2ivib<i> - 2nxQV - AQUiV + Aq2яа , Y= -2nQaio + 2nxQU+A(i(oU + AQ-2nQ~ .

Можно также заметить, гго Aq = M, где М' -масса жидкости, вытесненная цилиндром (на единицу толщины). Кроме того, если ©= О, то последние два члена в формуле (4) определяют присоединенную массу поступательного движения.

Последние формулы могут быть применены для получения результатов пп. 9.24, 9.25. Это мы предлагаем выполнить читателю в качестве упражнений.

Теорема Кутта - Жуковского (п. 7.45) следует как частный случай из формулы (4), потому что, положив ©=0, IT = const, мы получим

X + iY = 2nxQiW,

т. е. силу, действующую под прямым углом к направлению вектора W. Величина этой силы равна 2nxQ Vt/ + V* и не зависит от формы или площади поперечного сечения цилиндра. Уравнение (4) можно рассматривать, следовательно, как обобщение теоремы Кутта -Жуковского.

Соответствующие обобщения теоремы Лагалли, когда имеются источники и стоки, не представляют трудности.

9.62. Общий случай движения цилиндра. Комплексный потенциал в случае кругового цилиндра, движущегося перпендикулярно своей оси, был получен в п. 9.20 нз комплексного потенциала обтекания неподвижного цилиндра путем наложения на это течение потока, скорость которого противоположна скорости потока, обтекающего неподвижный цилиндр. Случай аналогичного движения эллиптического цилиндра можно получить подобным способом из обтекания неподвижного цилиндра с использованием результатов п. 6.33. Однако теперь мы изложим более общий метод, с помощью которого может быть непосредственно рещена задача о поступательном и вращательном движении произвольного цилиндра в жидкости, покоящейся на бесконечности.

В этом методе существенно используется конформное отображение области, внешней по отношению к поперечному сечению цилиндра в плоскости г, на внешность единичной окружности С = 1 в плоскости С Кроме того, используется формула (4) п. 9.40.

9.63. Комплексный потенциал движущегося цилиндра. Обозначим через С контур поперечного сечения цилиндра, который совершает двумерное движение в безграничной жидкости, покоящейся на бесконечности. Циркуляция около цилиндра отсутствует. Движение цилиндра определяется угловой скоростью ш и скоростью и точки О поперечного сечения цилиндра, причем скорость направлена под углом о к оси х (рис. 169). Предположим, что область вне цилиндра С в плоскости г (система координат имеет начало в точке О, связанной с цилиндром) может быть конформно отображена на внешность единичной окружности С I = 1 в плоскости комплексной переменной с помощью функции

г=/(а (1)

причем бесконечно удаленная точка z Рис. 169.

переходит в бесконечно удаленную точку

плоскости С- Тогда для жидкости, покоящейся на бесконечности, комплексный потенциал w не может содержать положительных степеней г (ИЛИ С) в разложении в степенной ряд по г (или Z).

Кроме того, на границе С цилиндра функция тока удовлетворяет соотношению [см. формулу (4) п. 9.40)

2/ф= -Uze-** + Uгe + iш2. (2)

Обозначим точку на единичной окружности через о, тогда

0=в*в, 0=е-*в=4-- (3)

Следовательно, на единичной окружности формула (2) принимает вид

21ф = В (о) = - г (0) e-< + в** + Ы (о) f(i)- (4)

Функцию в (а) удобно назвать граничной функцией. Если разложить ее в ряд по о, то можно записать

B(a) = Bi{a) + Bt(a), (5)

где функция Bt (о) содержит все отрицательные спепени о и ие содержит неотрицательных степеней. Таким образом, функция Bi(C) является аналитической вне единичного круга и обращается в нуль на бесконечности. Граничные условия (4) можно записать теперь в виде

Н - () = А. (о) + В, (а). (6)

Умножая это равенство на da/2ni{a-) и интегрируя по окружности единичного круга у> получаем

I Р a>(q)<to 1 Г (g)* 1 ( Bi(a)da 1 Р B2(a)da 2ж-J о-С 2ш-J ст-С 2ш j о-t 2h J а-f

(V) (V) (v) <Y)

Далее, функции w(X>) и Bi(C) являются аналитическими вне у> в то время как функции и в] (С) аналитичны внутри y- Следовательно,

если точка С лежит вне окружности у, то, применяя формулу Коиш (п. 5.59), найдем, что второй и четвертый интегралы обращаются в нуль. Вычисляя первый и третий интегралы, получаем равенство

w=Bi{l). (8)

Так как функция fli (С) содержит только отрицательные степени С. то условие обращения скорости в нуль на бесконечности также удовлетворено.

Чтобы показать, что найденная скорость жидкости всюду физически допустима, рассмотрим соотношение

-u+iv=w {z)=f§.

Преобразование (1) является конформным во всех точках вне контура, поэтому в жидкости не существует нулей функции / (С) и скорость жидкости всюду конечна.

Итак, с помощью преобразования (1) мы составляем граничную функцию (2), отделяем члены с отрицательными степенями С. которые стремятся к нулю, когда С|со. В результате получаем комплексный потенциал (8) как функцию С-

Если бы удалось с помощью формул (1) и (8) исключить С> то мы получили бы. конечно, комплексный потенциал как функцию z. Но во многих случаях проводить такое исключение или невозможно, или нежелательно.

Наконец, мы можем получить комплексный потенциал w обтекания цилиндра, положив в формуле (2) ш = О и наложив противоположно направленной поток со скоростью и. В результате этого можно получить соотношение

ш=В, {0+Uf(i)e-*\

9.64. Круговой цилиндр (общий метод). Простейшей иллюстрацией общего метода является случай кругового цилиндра радиуса а, движущегося

со скоростью £/, направленной под углом а к действительной оси. Если взять начало координат в центре поперечного сечения кругового цилиндра, то отображающая функция примет вид [см. формулу (1) п. 9.63]

z=al.

Граничная функция в этом случае выражается формулой

так что

следовательно.

В(1)=- £/aSe-* + £/ I в* + та*.

w=UaeJ = UaЧ^.

Как и следовало ожидать, в выражение комплексного потенциала не входит угловая скорость.

9.65. Эллиптический цилиндр. Если единичная окружность в комплексной плоскости S задана уравнением 1, = е^\ то преобразование

г = с(с + ). 0<Х<1 (1)

конформно отображает область, внешнюю к границе С, заданной уравнением

г= acosT)-!-J6sinT), (2)

где

а = с(1+Х), 6=с(1-Х), (3)

на область, внешнюю к единичной окружности, причем так, что бесконечно удаленная точка переходит в бесконечно удаленную точку. Ясно, что кривая С является эллипсом с осями 2а, 26. Эксцентрический угол точки г равен т). Заметим, что /()=0 только в точке

которая лежит внутри единичной окружности, так что отображение внешней области всюду конформно.

Граничная функция в данном случае имеет вид

В{1)=-Uce-<- +1) + (i + 0 + {+ + ( + )} откуда следует, что

Bt it) = - VUe- -Ь i/ce* 4- /шХс* ~ .

Таким образом, согласно формуле (8) п. 9.63, течение описывается комп.1ексным потенциалом

ш = л1 + 5. (4)

где вследствие формул (3)

Л=£/(6со8а+Ш8ша), 5 = о (а - 6 ). (5)

Если а = 6, то мы снова получаем движение кругового цилиндра.

Кинетическая энергия жидкости (приходящаяся на единицу толщины) дается интегралом (п. 9.10)

Т= -\ wdw, который берется по эллипсу С. Отсюда

turn

-TqJ (f+ )(i4 + 2Bt)dC- -iQ2ni(AA+2BB),

Г = 4 (pUJ* (6* cos* о + a sin o) + сяо) (a -6 ) .

Если {/bO (цилиндр вращается вокруг неподвижной оси), то

Г=1в о (а -6 ) ,

т. е. кинетическая энергия остается одинаковой для всех софокусных эллипсов. В частности, последнее равенство дает кинетическую энергию жидкости

в случае, когда эллипс вырождается в прямую линию, соединяющую фокусы.

ШТогда мы имеем случай вращающейся пластинки, однако скорость иа концах ч^ пластинки обращается в бесконечность, 1 так что это решение не может быть i- непосредственно применено к реальной жидкости. Случай вращающейся пластинки имеет особый интерес^). Для такой ~-.,с' , пластинки мы имеем 6 = 0, поэтому

X = 1, а = 2с; длина пластинки, согласно Рис. 170. формуле (3), равна 4с. Таким обра-

зом, из формулы (4) видно, что

ф= VtO>c* -ь . Чтобы найти линии тока относительно пластинки, наложим на движение угловую скорость-ш, добавив к величине ф функцию токл-У^(х*+у^= Полученная в результате функция тока относительного движения имеет вид

Линиями тока относительно пластинки являются линии const. На самой пластинке СС= Ь так как пластинка отображается в окружность единичного радиуса. Поэтому иа пластинке - шс*. Следовательно, разветвляющаяся линия тока в относительном движении задается уравнением У+ >с = 0, которое можно привести к виду

(K-i)(;v- +c+c)=o.

Первый множитель дает окружность, т. е. вращающуюся пластинку, а оставшаяся часть разветвляющейся линии тока описывается уравнением

;ч'-й+с*+; -о. (7)

Эта линия тока подходит к пластинке в точках К= 1, т. е. С*= - 1. поэтому г= ±-у^с. На рис. 170 эти точки обозначены буквами L и L, а концы

1) См. цитированную статью иа стр. 227.

пластинки-буквами А и А'. Пластинка вращается против часовой стрелки.

Кривая (7) пересекает ось в точке, где величина С становится чисто

мнимой, т. е. С = - С. откуда С*= -3, а 2= ± y На рис. 170 эти

точки обозначены буквами С и С. Таким образом, вместе с пластинкой разветвляющаяся линия тока образует две замкнутые петли, обозначенные на рисунке LCL и LCL.

Жидкость не может выйтн из этих петель и должна по необходимости вращаться вместе с вращающейся пластинкой, причем распределение скорости соответствует условию потенциальности движения. Внутри этих петель существуют относительные критические точки S и S (они получаются из условия дЧ/д^=0). Эти точки лежат на оси у на расстоянии, равном с(3/*-3~/*) = = 0,556с от центра пластины. Частицы в этих точках движутся так, как если бы они были жестко связаны с пластиной. На рис. 170 штриховые линии показывают относительные траектории других частиц.

Относительное движение частиц происходит по часовой стрелке, т. е. против направления вращения пластинки. В действительности относительная угловая скорость радиуса, проведенного нз центра пластинки к жидкой частице, меньше <о, так что существует общий дрейф жидкости против часовой стрелки, приводящий к появлению вращательной присоединенной массы (см. пример 8 к гл. 9).

Задачи, связанные с эллиптическими цилиндрами, могут быть также решены прямым методом, изложенным в п. 6.35. Так, если цилиндр движется поступательно со скоростью (/е *, то на границе мы имеем условие

ф= /т { - £/ze-* } = /т { - (Усе-* ch С},

записанное в эллиптических координатах. Следовательно, мы должны положить

ш= i/ce-* ch:-fF(C);

функцию F (С) надо выбрать так, чтобы на границе она обращалась в действительную функцию и чтобы w-*0, когда со. Если эллипс определен уравнением 1=1о, т. е. на границе С = 25о -С. то легко видеть, что функцию F (С) можно взять в виде

-ii/ce-* eC + l6ce e o-c.

w = U (а+Ь) s.h(lo + ) е--

Подобно этому для вращающегося эллиптического цилиндра на границе имеем

ф = -1о :*сЬСсН С-jwcch (С -С)-Ьconst.

Аналогичным образом можно получить, что

ш - iotc* ch (25 - 2о)- J <ос* sh (2S - 2о) = +

В общем случае если ф на границе является мнимой частью комплексного nortHmana Fi(0 + Ft{Z), где fi(t)- >оо, а f,(C)->() Ha бесконечности, то и = - Л(21о-С) + Л(С) прн условии, что функция fi(2 -О->0 на бесконечности.

Константа в этом соотношении не является существенной, поэтому

Чтобы найти траектории частиц относительно цилиндра, мы можем наложить на движение угловую скорость -с , добавив к функции тока ф член

-<й{х* + у*). Искомая функция тока получится в виде

9.66. Цилиндр с циркуляцией. Чтобы наложить циркуляцию на цилиндр произвольной формы, заметим, что мнимая часть комплексного потенциала

weixlnS (1)

на единичной окружности С = б' обращается в нуль, ф = х1п|С|=0, т. е. граница С при этом остается линией тока. Кроме того, .потенциал скорости - хт, так что ф уменьшается на 2як, когда мы обходим вокруг цилиндра в положительном направлении (против часовой стрелки). Таким образом, комплексный потенциал (1) дает циркуляцию 2пх вокруг цилиндра любой формы, который может быть отображен на единичную окружность. В частности, для эллиптического цилиндра (п.9.65) комплексный потенциал равен

a> = falnC+t/° °+ °+/. (2)

9.70. Вращающийся цилиндр. Пусть цилиндр, содержащий жидкость, вращается вокруг оси, проходящей через начало координат параллельно образующей цилиндра; тогда можно использовать следующие соображения.

Пусть уравнение границы поперечного сечения записано в виде

= /(2)+ 7(2). (1)

где функция / (г) ие имеет особенностей внутри контура поперечного сечения цилиндра; тогда задача решается комплексным потенциалом

и> = ШПг), (2)

так как в этом случае на границе ф=-шгг.

Если все особенности функции / (г) лежат внутри контура, то формула (2) дает решение задачи о цилиндре, вращающемся в жидкости.

В общем случае если уравнение z = F (С) определяет некоторую систему координат, например эллиптическую, такую, что на границе

= / )+/( .

то функция w = iaf{l) является комплексным потенциалом для жидкости, движущейся внутри или вне цилиндра в зависимости от того, вне или внутри контура цилиндра находятся особенности функции dw/dz, т. е. функции г цуг (!;,).

9.71. Вращающийся эллиптический цилиндр, содержащий жидкость. Возьмем поперечное сечение цилиндра в виде эллипса

пли +)* 1

в 6 ~ 4а 46

Сравнивая последнее равенство с формулой (1) п. 9.70, получаем

К,\ 1 а*-Ь* , в Ь