Мы можем теперь выполнить обобщение на случай произвольного двумерного безвихревого движения жидкости между двумя твердыми цилиндрами Ci и С]. Комплексный потенциал любого такого движения может быть выражен в виде суммы w+wo, где ш-потенциал ациклического движения, а Wo - потенциал циклического движения с неподвижными границами. В этом случае полная кинетическая энергия жидкости (на единицу толщины) выражается следующей формулой:

r=lQj (w+Wo){dw+dwo)= I/qJ wdw + jiQ{ wdwo + T, (5)

(с) (с) (с)

7=j/qJ ( da>e-ba>oda>) = -J/Q j {a (d o-2dфo)--(ш o-f 2Фо)Лр}.

где

Далее, по теореме Коши \ wdw9= \ Wndw-Q; функция фо, как и

(с) (с)

прежде, постоянна на границах С| и С|. Следовательно, 7 = yQ J ( йфо-фо) = 0,

так как функции а> и фо являются однозначными и интегралы вдоль линий АВ и ВА сокращаются. Таким образом,

Г=.в5 шЛгг-1-яхс1(ф,)в-(фо)А1,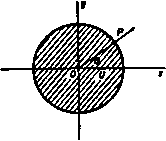

Рнс. 162.

другими словами, кинетическая энергия Т является суммой кинетических энергий каждого движения, если их рассматривать независимо. Так как функция W однозначна, то интеграл в формуле (6) ие зависит от перегородки АВ.

В качестве примера вычисления кинетической энергии циклического движения рассмотрим случай движения с циркуляцией интенсивности x между двумя круговыми цилиндрами радиусов а и 6 (п. 7.11). В этом случае

Т= nxQix Inft -x lna) = nx*Qln.

9.20. Круговой цилиндр, движущийся поступательно. Рассмотрим цилиндр радиуса а, помещенный в поток жидкости, у которого скорость на бесконечности направлена вдоль

отрицательной части оси х и равна U (рис. 162). Возьмем начало координат в центре цилиндра, тогда, согласно п. 6.22, комплексный потенциал течения имеет вид

Если мы наложим на наше течение поток, скорость которого равна V и направлена вдоль положительной части осн х, то получим цилиндр, движущийся со скоростью и в жидкости, которая покоится на бесконечности. Потенциал этого течения задается формулой

=.. О)

Сравнивая эту формулу с результатами п. 8.23, мы видим, что комп-.1ексный потенциал нашего течения в точности совпадает с потенциалом

ПЛОСКОГО диполя, помещеииого в центр цилиндра. Ось этого диполя направлена вдоль положительны! части оси х, а интенсивность равна Ua. Из формулы (1) получаем комплексную скорость течения

и -to-.

Отсюда радиальная и трансверсальная ктшоненты скорости в точке с координатами {г, 6) выражаются формулами

f/a cose (/aslne

7i * г

Следует подчеркнуть, что эти выражения являются компонентами абсолютной скорости жидкости в движущихся осях для фиксированной точки пространства, координаты которой в рассматриваемый момент времени равны гид. Единственное свойство, которое требуется от комплексного потенциала, это то, чтобы его производная давала бы выражение для скорости. Учитывая также, что

получаем, что скорость имеет одну и ту же величину во всех точках, равноудаленных от центра цилиндра. В частности, q=:U при г=а, т. е. скорость на поверхности цилиндра равна U.

9.21. Траектории частиц. Рассмотрим фиксированные оси Ох и Оу в тот момент времени, когда центр цилиндра совпадает с точкой О (рис. 163). Частица, находящаяся в точке Р{х, у), движется со скоростью UaVr*,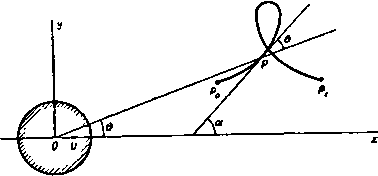

Рис. 163.

направленной под углом в к радиусу-вектору (п. 9.20). Следовательно, касательная к траектории в точке Р составляет с осью Ох угол о =20, Отсюда, если /? -радиус кривизны траектории в точке Р, то

J da d(2Q) dy db .

R -4k---djT ®*

Далее, когда жидкость обтекает неподвижный цилиндр, то частица Р движется вдоль линии тока, уравнение которой (п. 6.22)) имеет вид

) Это соотношение между у и в имеет место для наблюдателя, движущегося вместе с вилиидром. Когда цилиндр неподвижен, данное соотношение является уравнением линии тока.

Продифференцируем последнее равенство по у; после несложных преобразований получим

Следовательно,

-sl 2e=(i,-i,).

Мы получили уравнение эластики, т. е. кривой, форму которой принимает абсолютно гибкий прут, подверженный продольному сжатию. Когда цилиндр движется из - со в + со, точка Р движется из точки Ро в точку Pi, которые являются точками эластики и в которых касательная параллельна оси X.

Теперь вычислим дрейфе) точки Р, т. е. длину отрезка 6 = ЯоЯ| (см. рис. 163).

В дальнейшем мы будем рассматривать движение жидкости по отношению к цилиндру, который будем считать неподвижным, т. е. жидкость будет двигаться справа налево со скоростью U. Используя выражение для радиальной и трансверсальной компонент скорости из п. 9.20, мы получаем следующие уравнения для относительного движения:

- = -9(-1), -sino(+l), ,2)

Один из интегралов этих уравнений есть функция тока (1), где постоянная 11 задает начальное и конечное расстояние частицы от линии движения центра цилиндра. Тогда из формул (1) и (2) находим величину дрейфа в виде

-со о

Это движение может быть описано эллиптическими функциями, если положить

и со5в= - sno, откуда следует, что v изменяется от -/С до К, где К - полный эллиптический интеграл первого рода. Тогда все движение выразится через параметр v с помощью формул

i(o) = (ft + dnt ). 6(i) = j{(l-**)w-£( )

t (t ) = sci;(ft-fdnr)-bS(w).

где \(v), /( ) -декартовы координаты частицы в момент времени / (i) относительно первоначального невозмущенного положения.

Эти уравнения дают нам возможность построить траектории) и вычислить величину дрейфа

Е=¥{(-у*)- }- <5)

) Этот термин и соответствующее исследование, изложенное ниже появились благодаря Дарвину, который, по-видимому, был первым, кто дал физически удовлетворительную интуитивную картину этого явления и ввел понятие виртуальной массы. См Darwin С. Ргос. СатЬг. Phil. Soc, 49 (1953), 342-354.

*) Milne-Thomson L. М., Jacobian elliptic function tables, N.Y., 1958.

Некоторые из этих траекторий показаны на рис. 164, взятом из статьи Дарвина. Начало отсчета времени соответствует моменту положения цилиндра в начале координат. Цифры на кривых отмечают выбранные в подходящем масштабе моменты времени, в которые частицы находились в данных положениях. Так, например, точка на кривой, отмеченная цифрой 2, дает положение жидкой частицы, когда цилиндр продвинулся вперед на 2 радиуса от начального положения. Для рассматриваемых частиц жидкости штриховая кривая в левой части рисунка показывает начальные положения частиц, когда цилиндр находился в -с , а штриховая кривая в правой части - конечные положения частиц, когда цилиндр ушел в --оо.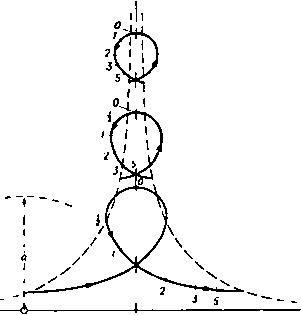

Рис. 164.

Таким образом, в самом деле существует дрейф жидкости слева направо. Масса жидкости между начальным и конечным положением частиц (берется слой жидкости единичной толщины) может быть названа дрейф-массой qD и вычислена по формуле

+а>

qD=.q5Ut. (6)

Непосредственным интегрированием можно показать, что qD = na*q = М', т. е. массе жидкости, вытесненной цилиндром.

9.22. Кинетическая энергия. Если круговой цилиндр радиуса а движется в жидкости поступательно со скоростью U, то кинетическая энергия жидкости определяется по формуле

Г/= - jQ wdw.

Кроме того,

- Ua*

.- Ua* -

Далее, на поверхности цилиндра г = ае, 2=ае-*, dz= -iae-* dQ, так что

Т,= -1Q i/ae-ede = l ea f/ .

Пусть М'= яоа*. Очевидно, М' есть масса жидкости (приходящаяся на единицу толщины), вытесненная цилиндром.

Тогда если Л1 -масса цилиндра, приходящаяся на единицу толщины, то общая кинетическая энергия жидкости и цилиндра равна

Обозначим через F внешнюю силу, действующую в направлении движения цилиндра и необходимую для поддержания его движения. Тогда мощность силы F должна быть равна скорости увеличения общей кинетической энергии и. следовательно.

FU==(M + M)UJ,

F-M at=dr

Если бы жидкость отсутствовала, второй член в левой части последнего уравнения обратился бы в нуль. Таким образом, вследствие присутствия жидкости цилиндр при движении испытывает сопротивление, величина которого (приходящаяся на единицу толщины жидкости) равна

di-

9.221. Виртуальная масса. Из последнего уравнения п. 9.22 следует, что присутствие жидкости увеличивает массу движущегося цилиндра от М до уИ-f/kl. где уИ -масса вытесненной жидкости. Масса М + М' называется виртуальной массой цилиндра). Виртуальная масса получается увеличением массы цилиндра М на присоединенную массу, или гидродинамическую массу, которая в случае кругового цилиндра равна М'. Заметим, что эта гидродинамическая масса М' равна дрейф-массе qD, вычисленной в п. 9.21. Оказывается, что все движущиеся тела, если движение происходит в некоторой сплошной среде, как бы приобретают добавочную массу, так что во всех динамических экспериментах массы проявляются как виртуальные массы типа M-kM, где коэффициент k зависит от формы тела и типа движения. Дарвин в цитированной выше статье доказал, что для тела, движущегося прямолинейно в неограниченной жидкости, гидродинамическая масса равна дрейф-массе, т. е.

kM = QD, а в случае кругового цилиндра ft = 1.

9.222. Виртуальная масса в двумерном движении. Рассмотрим цилиндр произвольной формы, совершающий в неограниченной жидкости прямолинейное плоское движение со скоростью U. В системе координат, связанной с цилиндром, течение описывается комплексным потенциалом w=Uz + -i-(/-r g)- Если ввести потенциал скорости ф и функцию тока ф, то

>) В отечественной литературе обычно рассматривается масса М', называемая присоединенной массой цилиндра.- pujK. перев.

получим

Ф= t = Uy+g (I)

Так как функция f + ig описывает возмущение, вносимое в течение присутствием цилиндра, то эта функция должна стремиться к нулю на бесконечности и, следовательно, может быть разложена в ряд по отрицательным степеням г. Отсюда следует, что и функции ф и могут быть разложены в ряды по отрицательным степеням г, причем члены рядов будут стремиться к нулю на бесконечности. Таким образом, мы имеем

9-их + + + +.... (2)

-(у-+-+--- (3)

Граничные условия могут быть выражены или в виде

фв const на границе тела, (4)

или в виде

Ifx + mfg -UI на границе тела, (5)

где (/, т) - направляющие косинусы внешней нормали иа границе тела, а индексы означают частное дифференцирование. Движение частицы задается уравнениями

-=-и-Ы, g=-/,. (6)

Функция тока дает один интеграл этих уравнений вида

yp=Uy+g=Ur\, (7)

где постоянная г\ определяет асимптоты к линиям тока в -f оо и - оо. Кроме того, вследствие уравнений Коши-Римана (1) п. 6.0 имеют место равенства

где д (ф, ф)/д (jc, у) - якобиан. Таким образом, величина дрейфа I задается формулой

-оо -оо

Здесь в подннтегральном выражении необходимо перейти от переменных X, у к переменным ф, ф. Тогда интегрирование должно производиться по переменной ф при постоянной ф.

Дрейф-объем D определяется теперь по формуле

D= f =И S (-М ф = 5 5 (-U)dxdy. (9)

Здесь область интегрирования распространяется на всю плоскость движения, кроме поперечного сечения цилиндра. Но важно заметить, что интеграл сходится не абсолютно и может принимать разные значения в зависимости от порядка интегрирования. В настоящем случае, без сомнения, должно быть выполнено сначала интегрирование по ф, а после - по ф. Так как вдали от цилиндра функция qiUx, ypUy (что видно из формул (2) и (3)1, тб в последнем интеграле формулы (9) первым должно быть выполнено интегрирование по х. Это означает, что величина D

вычисляется следующим образом: надо взять интеграл по области х= ±Х и у=±ц. затем Яиц устремить к бесконечности. Тогда порядок стремления Я к бесконечности должен быть больше, чем порядок стремления i. Рассмотрим возможные значения интеграла

J= 11 {-U)dxdy= 5 5 (U-v,)dxdy. (10)

Применим теорему Стока и введем функцию тока ф, тогда рассматриваемый интеграл прео15разуется к виду

(0) (00)

У= J J {U-%)dxdy= - J (Uy-) mds- 5 {Uy-)mds, (11)

где (0) обозначает интегрирование по поверхности тела, а (оо)-интегрирование по поверхности, удаленной на бесконечность. Далее, вследствие условия (4) величина ф постоянна на поверхности тела, поэтому соответствующий интеграл обращается в нуль, тогда как

\ ymdsV, (12)

где V-объем тела.

Таким образом, первый член правой части равенства (11) всегда дает - VU. Что касается второго члена, то определим область интегрирования как ящик х=±Я, у=±\1, где и Я и ц должны быть устремлены в бесконечность. Подставим формулу (3) в последний член равенства (И), тогда легко видеть, что только один член ряда дает интеграл, отличный от нуля. В результате получим

J = -VU + iAaTctg . (13)

Таким образом, крайними значениями, которые может принимать интеграл являются величины

У = - VU, когда ц велико по сравнению с Я, (14)

J = 2nA-VU, когда ц мало по сравнению с Я. (15)

Покажем, что величина (15) пропорциональна гидродинамической массе. Мы уже видели, что когда Я велико по сравнению с то формула (9) определяет дрейф-объем, так что в этом случае J = DU. Однако существуют и другие интерпретации. В системе координат, в которой движется тело, скорость жидкости в направлении оси х равна u = f/-ф^. Общий

расход жидкости через любую трансверсальную плоскость равен udy.

Полный перенос жидкости равен интегралу по времени от последнего выражения; интеграл по времени, умноженный на величину V, есть интеграл по х, который равен интегралу J. Отсюда следует, что интеграл по времени равен J/U. Здесь интегрирование по у проводится первым, т. е. мы должны взять i по порядку большим, чем Я, и в результате интегрирования fcM. формулу (14)] мы получаем величину -К, количество жидкости, вытесненной телом.

Если Q -плотность жидкости, то количество движения жидкости выражается интегралом

Qudxdy=Qj, (16)

Кинетическая энергия жидкости равна

-1я(/ = j J\Q{(U-4>.) + 4>l}dxdy. (17)

Этот интеграл является абсолютно сходящимся и определяет гидродинамическую массу Н. Но если гидродинамическая масса Н входит в выражение для кинетической энергии, то она должна также входить в выражение для количества движения. Поэтому равенства (16) и (17) должны быть взаимосвязаны. Это и на самом деле следует из равенств (16) и (17). Составим разность

==9\\{li<f-xU)4 + §-(<f-xU)q>y}dxdy =

(18)

= - в jj (Ф - Щ (/ф, -t- тф ) ds - в J (ф - Ux) (/ф, + т%) ds.

Здесь мы воспользовались теоремой Стокса и равенством u=U - (fx.

Далее, вследствие формулы (5) на поверхности тела /ф1 + тф = 0, тогда как на бесконечности, как следует из формулы (2), ф^-а ф„-0. Поэтому только главный член в разложении (2) дает отличный от нуля интеграл в формуле (18), который равен 4Л arctg ц/Я. Таким образом, если ц мало по сравнению с Я., то из формул (15) и (18) следует

HU-Jq=0, J=2nA-VU,

т. с. гидродинамическая масса равна

(2nA--VU)Q П=-jj-.

Это доказывает, что в безграничной жидкости дрейф-объем определяет гидродинамическую массу. Таким образом, присоединенная масса действительно представляет собой массу жидкости, заключенную в цилиндре.

С

9.23. Круговой цилиндр, падающий под действием силы тяжести. Предположим, что цилиндр радиуса а и плотности а, ось которого остается горизонтальной, падает в жидкости плотности q. Будем рассматривать цилиндр единичной длины, ограниченный гладкими вертикальными стенками (рис. 165); тогда его вес равен na*<sg.

По закону Архимеда со стороны жидкости на цилиндр действует подъемная сила, равная яа^{. Рис. 165. Отсюда следует, что действующая на цилиндр вертикальная сила равна ла*(о-q)£r и направлена вниз. Если обозначить через у глубину жидкости, отсчитываемую по вертикали от поверхности, то, согласно п. 9.22, уравнение движения цилиндра

имеет вид

()тсюда

d*y о -Q

т. е. цилиндр падает с постоянным ускорением при условии, что величина у достаточно велика, чтобы можно было не учитывать условия на поверхности жидкости. Когда о < q, что имеет место в случае баллона, цилиндр

поднимается с ускорением gff-

9.24. Круговой цилиндр с циркуляцией. Пусть цилиндр поперечного кругового сечения радиуса а с центром С движется со скоростью U-\-iV и пусть в момент времени / центр С находится в точке г. Тогда

z = U-\-iV, (1)

где точкой обозначено дифференцирование по времени. Если циркуляция

равна 2ях, то на цилиндр действует подъемная сила, равная 2nnQU

(см. п. 7.45). Кроме того, так как ускорение центра г отлично от нуля,

то существует еще сила сопротивления, равная -М'г (п. 9.22).

Таким образом, со стороны жидкости на цилиндр действует сила

X+iY=- М'г + 2nxQiz.

Если больше нет никаких внешних сил. то уравнение движения цилиндра массы М имеет вид

Mz=X + iY.

(М + М') Z- 2nnQiz = 0. (2)

Интеграл этого линейного дифференциального уравнения второго порядка с постоянными коэффициентами может быть найден или подобран в виде

г=го + АеНш.е), 0.= -..

где Ае* и Zg -произвольные постоянные, причем Л - действительная величина. Отсюда получим

г-го = Л.

т. е. центр цилиндра описывает окружность с центром в точке Zq. Кроме того,

U+iV=z = i<aAe < >+ ).

т. е. эта окружность описывается с постоянной скоростью, причем одни оборот совершается за время 2п/(а, а радиус этой окружности равен

~ 2лхе

9.25. Цилиндр с циркуляцией, движущийся под действием силы

тяжести. Пусть на цилиндр, рассмотренный в п. 9.24, действует еще сила тяжести. Пусть ось цилиндра направлена горизонтально, а ось у вертикально вверх. Сила тяжести, действующая на цилиндр, направлена вниз и равна Mg; кроме того, на цилиндр действует архимедова сила Mg. направленная вертикально вверх. Следовательно, уравнение (1) п. 9.24 принимает вид

(М+М') Z- 2яхв/г = -i{M-M)g,

шли

z - i<az= -igo,

где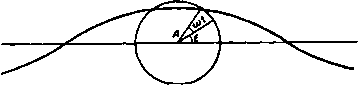

Рис. 166.

вращается с угловой скоростью ш. в то время как центр круга движется вдоль горизонтальной прямой с постоянной скоростью go/a (рис. 166).

Точная величина радиуса А будет зависеть от начальной скорости и направления движения центра цилиндра. Эти величины можно подобрать так, что А = 0, тогда траектория центра будет прямой линией. Кроме того, когда траектория является трохоидой, движение в среднем направлено

горизонтально. Другими словами, цилиндр ие проявляет тенденции погрузиться под дейст->уW вием силы тяжести. Это явление может быть

хт \ выдвинуто в качестве некоторого объяснения

X \ наблюдающегося поведения теннисного мяча.

i* 9.30. Уравнение для давления в движу-

и щейся системе координат. Пусть начало коор-

динат имеет составляющие скорости U и V Рис. 167. вдоль мгновенного положения осей, и пусть

ш - угловая скорость вращения системы координат. Уравнение для давления было выведено в п. 3.61. Чтобы применить его к нашему случаю, мы должны вычислить квадрат скорости в точке г (рис. 167). В данном случае, сохраняя обозначения пп. 3.61 и 5.10, для скорости в точке г мы получаем следующее выражение:

U + vtXr = lU + iV + u>kx{x\-\-yi)>~l(U - y<u) + (y + x<u)kx]i = {W-\-i<az)i.

где W = U + iV. Таким образом, квадрат скорости в точке г равен

{W+im)(W-iioz),

а уравнение, определяющее давление, имеет вид

+ + 5-(Я^ + шг)(Г-шг) = С(/),

где (7г -скорость жидкости относительно движущихся осей.

Если относительное движение установившееся, как, например, в случае наблюдателя, находящегося на корабле, который движется с постоянной скоростью по постоянному курсу, то уравнение для давления принимает вид

+q + Q-.(W + шг) (TF- iW) = С,

где С -теперь некоторая постоянная.

Ясно, что частное решение этого уравиеиия имеет вид z = got/ф и, еле довательно. общее решение уравнения задается формулой

2 = го+ .

Отсюда х=>Хо + +Acos{<at + t), y = yQ + Asm(iotA-t).

Таким образом, траекторией центра цилиндра является трохоида, описы ваемая точкой, расположенной на окружности круга радиуса А, который