момент отраженного

ж

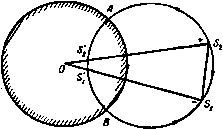Рнс. 157.

Поскольку OA = OSiOS\, то прямая OA касается окружности S,S25jS и, следовательно, две окружности пересекаются ортогонально в точках А и В (ср. п. 4.6).

Направление потока на разветвляющейся линии тока указано на рис. 157.

8.81. Отображение диполя относительно кругового цилиндра. Пусть точка S, на рис. 157 приближается к точке Sj, тогда как произведение mSiSt = \i остается конечным. В пределе мы получим диполь с моментом р; построим его отображение относительно окружности.

Так как треугольники OSjSj и OSjSj подобны, то

SjSt OSi SiSz ~ OSz (Следовательно, диполя равен

где точка С характеризует положение диполя с моментом р. а точка D характеризует положение диполя с моментом ц' (рис. 158). Поскольку С и D - есть инверсии, то если ОС = f, то OD=aVf и поэтому

Обращаясь снова к рис. 157, мы видим, что если точка Si в пределе совпадает с точкой 5j, то окружность, проходящая через точки SiS,SiSJ, ш'ресечет оси диполей в точках С и D. Следовательно, отображением

диполя с моментом (i, находящегося на расстоянии f от центра цилиндра радиуса а, является диполь в точке инверсии с моментом Оси

диполя и его отображения одинаково наклонены к соединяющей их линии, но не параллельны. (Такие линии удобно называть антипараллельными.)

Вышеуказанная окружность, которая касается осей диполя в точках С и D, по-прежнему является линией тока и пересекает цилиндр в точках i4 и В.

Рис. 158. 8.82. Сила, действующая на ци-

линдр, обусловленная диполем. Пусть диполь находится на расстоянии f от центра цилиндра радиуса а и помешается на действительной оси, как показано на рис. 158.

Пусть (1 и а обозначают момент и угол наклона диполя. Тогда если ff=a*. то мы имеем (см. п. 8.23) комплексный потенциал вида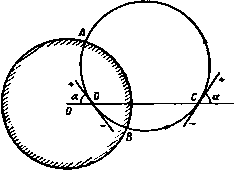

г-f ft г-f

причем второй член обусловлен наличием в точке D отображения диполя, находящегося в точке С. Отсюда получаем следующее соотношение:

X-iY = -iQ2ni-

(ft-а*)

л - (/i e ) -

Полученное выражение для силы, действующей на единицу длины цилиндра, показывает, что цилиндр движется по направлению к диполю. Интересно отметить, что сила не зависит от ориентации диполя.

Так как все силы давления, действующие на границу, проходят через центр цилиндра, то момент этих сил относительно центра равен нулю.

8.83. Распространение теоремы Лагалли на диполи. Диполю в комплексном потенциале будет соответствовать член \ieV(z-a). Таким образом, в обозначениях п. 8.63 имеем

члены, содержащие множитель т, теперь исчезнут. Формула (5) п. 8.63 примет вид

где /(z) снова обозначает часть комплексной скорости, полученной отбрасыванием диполя в комплексном потенциале. По теореме Тейлора имеем

f (Z) = / 1{г-а) +а] = f{a)+ (г-а) f (а) + ... .

Вычет в точке г=а оказывается равным 2°/(а). Таким образом, формула (6) п. 8.63 принимает вид

X-iY= - 2nQix (fJ - iV) -f- 2nQ(ie* / (a).

Это и есть искомое обобщение теоремы Лагалли.

Для того чтобы применить эту формулу к случаю п. 8.82, отбросим в комплексном потенциале w член, обусловленный диполем в точке z=f. Тогда получим

Согласно теореме Чаплыгина - Блазиуса, результирующую силу можно записать в виде

Здесь интеграл берется по окружности. Единственным полкхгом внутри контура является точка z = /. Следовательно, вычет представляет собой коэффициент при (z-/) если третий член вышеприведенного соотношения записать в виде суммы простых дробей или разложить по возрастающим степеням (z-/). Положим j/ = z - /, тогда искомое разложение можно записать следующим образом:

> ! !-rl V

г-n{г-n~ У^(y+r-f) ~ yHf-fTK f-fJ ~

~ У (/-/) V /-/ + (/-/) J Отсюда коэффициент при (z -/) , или y~ равен

2 2/

(/-/) ~ (/ -а )

Следовательно,

Следовательно, как прежде, получим формулу

8.90. Источник в сжимаемом потоке. Пусть имеется двумерный источник мощности 2лт в единицу времени и пусть q обозначает скорость на расстоянии г от источника (рис. 159). Тогда уравнение неразрывности дает

2пге<7 = 2пт,

откуда, используя обозначения п. 1.63 и формулу (7) п. 1.63, получаем

т

т

1+ (Y 1)M

2(V-1)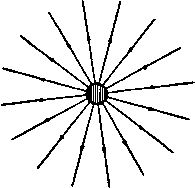

где М -число Маха.

Дифференцируя это соотнощение по М, р и с. 159.

легко показать, что г имеет минимальное значение при М = 1, и, следовательно, по формуле (1) получаем

г Г 2 , Y- мЛ*

Таким образом, движение жидкости имеется только вне окружности радиуса fmin и не может быть продолжено внутрь окружности. Следовательно, для размера источника имеется физическая нижняя грань. Источник не может сжаться в точку. Вне окружности мы имеем или чисто дозвуковой поток, в котором q постепенно уменьшается до тех пор, пока число М не станет равным нулю в бесконечности, или сверхзвуковой поток, в котором q постоянно увеличивается до тех пор, пока число М не станет равным бесконечности в бесконечности. Такие потоки могут иметь место между двумя твердыми плоскостями, наклоненными под углом, как показано на рис. 152, при этом источник находится в угловой точке.

ПРИМЕРЫ К ГЛАВЕ 8

1. Построить по методу Рэикнна линии тока для течения, обусловленного двумя равными по мощности источниками.

2. Провести линии тока для течения, обусловленного равными по мощности источником и стоком в двух случаях:

(I) когда только они одни находятся в жидкости;

(II) когда они расположены в течении, перпендикулярном к линии, соединяющей источник и сток.

S. Источник и сток одинаковой мощности помещены на данном расстоянии друг от друга в бесконечной покоящейся жидкости. Показать, что линиями тока являются окружности и что скорость жидкости вдоль любой линии тока обратно пропорциональна расстоянию до линии, соединяющей источник и сток.

4. Два источника одинаковой мощности расположены соответственно в точках (±4. О) неограниченной жидкости. Показать, что в любой точке окружности дг*4-у*=<* скорость движения жидкости параллельна оси у и обратно пропорциональна координате точки. Требуется также определить точку оси у, в которой скорость наибольшая.

Показать, что если равномерный поток, параллельный осн у, скомбинировать с двумя источниками, то обязательно существуют две точки, в которых скорость обращаетса иуль.

с ах . 2Ь*ху \

Vl+lxS+yWJ

5. Пусть в точке А имеется источник мощности т, а в точке В -сток мощности -т. Пусть равномерный поток со скоростью U направлен по ВА. Найти критические точки и доказать, что оии лежат на линии АВ или на перпендикуляре к ней, проведенном в ее середине, в зависимости от величины скорости потока. Провести в каждом случае линии тока.

в. Имеется источник в точке А и равный ему по мощности сток в точке В. Линия АВ совпадает с направлением равномерного потока. Определить форму линий тока. Пусть точка А имеет координаты (в, 0), точка В-координаты (-о, 0); пусть отношение величины потока жидкости, вытекающего из точки А в единицу времени к скорости потока, равно 2пЬ. Показать, что функция тока имеет вид

*=Vl,-V*arctg5:,-.

Доказать, что характерные размеры овала (длина 21, ширина 2d), который представляет собой часть разветвляющейся линии тока, определяютси формулами

Доказать также, что геометрическое место точек, в которых скорость равна скорости равномерного потока, имеет следующий вид

х*-у*=а*+аЬ.

7. Двумерный источник мощности т расположен в точке (о, 0); при этом ось у является неподвижной границей. Найти на границе точки, в которых скорость жидкости имеет максимальное значение.

Показать, что результирующее давление на ту часть оси у, которая находится между точками у=Ь, равно

2p.*-2m e{-arctgA * },

где Ро -давление в бесконечности.

8. Определить действующую на стенку силу, вызванную диполем с моментом и, находящимся на расстоянии а от стенки и с осью, наклоненной к ней под углом а. По какому направлению действует эта сила иа стенку/

9. Доказать, что при конформном преобразовании диполь преобразуется в диполь, ио что моменты этих диполей будут различны.

to. Два источника, каждый мощности т, помещены в точках (-а, 0) и (а, 0): сток мощности 2т помещен в начале координат. Показать, что линиями тока являются фивые

x+y) = aHx-y+)y),

где X-переменный параметр.

Показать также, что скорость жидкости в любой точке равна

где /-1, Г2, Гз-соответственно расстояния точки от источников и стока.

11. Если в точках (о, 0), (-о, 0) имеются источники и в точках (О, а), (О, -а) стоки, причем все одинаковой мощности, то показать, что окружность, проходящая через эти четыре точки, является линией тока.

12. Пусть оси Ох, Оу являются неподвижными твердыми границами и пусть в точке (о, Ь) находится источник. Найти вид лннни тока и показать, что разветвляющаяся линия тока определяется уравнением

ху(х*-у'-а'+Ь*)=0.

13. В жидкости, ограниченной осями х и у, в первом квадранте иа биссектрисе угла хОу на расстоянии а от начала координат имеется источник мощности т. Доказать, что комплексный потенциал течения имеет вид -m\n{a*-\-i*).

14. Между неподвижными границами в = я/4 и в=-я/4 имеется двумерное движение, которое создается источником мощности m в точке г=а, 6 = 0 и равным по мощности стоком в точке г=Ь, 6=0. Показать, что функция тока имеет вид

*- ягг ., M(a -M)s!n4e

15. Показать, что компоненты скорости, задаваемые формулами

Примеры 219

представляют возможное двумерное движение жидкости. Показать, что это движение безвихревое, и выяснить смысл членов, входящих в выражение комплексного потенциала.

1в. Пусть дан равносторонний треугольник ABC. Имеются источник мощности 2 единицы в точке А и стоки мощности 1 единица в точках В С. Пусть имеется равномерный поток, направленный от точки А перпендикулярно к ВС. Определить вид линий тока, если относительные мощности таковы, что разветвляющаяся линия тока частично состоит из преграждающей стенки.

17. Показать, что комплексный потенциал i =x In (г*-/ ) задает движение жидкости, обусловленное двумерным источником при наличии неподвижной стенки. С помощью преобразования, определяемого формулой

dl А

dz (г1 1) /

получить рещение для такого источника в полубесконечном прямоугольнике.

18. Используя преобразование 2 = °, найти линии тока двумерного движения, обусловленного источником, находящимся посредине между двумя бесконечно длинными параллельными границами, предполагая, что жидкость вытекает через стоки в конце области. Если давление стремится к нулю на концах потока, то доказать, что на плоскости действуют силы, изменяющиеся обратно пропорционально расстоянию между плоскостями.

19. Источник помещен посредине между двумя плоскостями, отстоящими друг от друга на расстоянии 2а. Найти уравнение линий тока в двумерном движении и показать, что те частицы, которые в бесконечности находятся на расстоянии /зa от одной нз границ, вытекают из источника в направлении, образующем угол л/4 с этой границей.

20. Безвихревое двумерное движение жидкости, ограниченное линиями у=4:Ь, обу-с.ювлено диполем с моментом ц, находящимся в начале координат, при этом ось диполя совпадает с положительным направлением осн х. Доказать, что движение дается формулой

<f+i=cb 1я1х+{у)/Щ.

Показать также, что кривая ch (лх/Ь) = sec (л| 6) является геометрическим местом точек, скорости которых параллельны осн у.

21. Пространство с одной стороны бесконечно длинной плоской стены у = 0 заполнено невязкой несжимаемой жидкостью, движущейся в бесконечности со скоростью U в направлении оси X. Движение двумерное и происходит в плоскости (х, у). Диполь с моментом 1 находится на расстоянии а от стенки, ось диполя направлена вдоль отрицательной части оси X. Показать, что если ц меньще, чем 4вЧ/, то давление жидкости на стенку максимально в точках, находящихся иа расстоянии аУЪ от точки О -основания перпендикуляра, опущенного из центра диполя на стенку; показать также, что давление минимально в точке О.

Если 1 = 4аЧ/, то найти критические точки и показать, что семейство линий тока содержит в себе окружность х*+(у-а)* = 4а*, причем начало координат находится в точке О.

22. Рассмотрим двумерное движение жидкости. Имеются источники полной мощности 2ят, равномерно распределенные вдоль действительной оси на отрезке от х - 0 до х=а. Показать, что соответствующий комплексный потенциал равен

а

ю= - In (г-У<<5= -m In г- In (г-а). о

Скомбинировать это движение с равномерным потоком скорости U, параллельным ни X, и показать, что разветвляющаяся линия тока задается уравнением

f/ -f-{(e2-e,)-f овг-Ьу In--яа}- = 0.

где г расстояния и 61, вг-соответствующие углы, которые образуют лучи, проведенные из точек этой линии к крайним источникам. Изобразить графически вид этих линий.

S3. Вдоль оси X на каждом участке от х=2па до х=(2л--1)а имеется двумерный источник мощности к на единицу длины, а на каждом участке от х=(2п-1)а до х=2па-двумерный сток такой же мощности, причем п принимает все положительные и отрицательные целые значения. Если tv-комплексный потенциал, то найтн ~dw/dz.

Если в канале, ограниченном стенками х=в и х=-а, имеются равномерно распределенные источники, расположенные на отрезке от х=0 до х = а, и равной мощности стоки, расположенные на отрезке от х=0 до х=-а, то требуется найти скорость в ли>-*вЛ точке вдоль стенок канала.

30. Двумерный источник / мощности m расположен вне неподвижной окружности с центром в точке С. Доказать, что скорость q в любой точке Р равна mrrjrfirz, где через г, гу, rj, г / обозначены расстояния точки соответственно до точек С, I, J, А, В, прн этом /-центр источника, 7 -инверсия точки /, у4 и В-точки, в которых прямая С/ пересекает окружность.

31. Пусть окружность, рассеченная пополам осью у, образует вместе с этой осью твердую границу и пусть на оси х помещен источник мощности m на расстоянии а от центра, равном половине радиуса. Доказать, что уравнение линий тока имеет вид

(16o*--r4)cos2e-17aV =(16a -r )sln2ectg() ,

где Ь-зиачення функции тока.

показать, что линия тока ф=/пя/2 выходит из источника в направлении, перпендикулярном оси Ох, а входит в сток под углом я/4 к оси Ох; начертить линии тока.

32. При двумерном движении бесконечной жидкости имеется твердая граница, состоящая из части окружности х*-{-у>=а*, занимающей первый и четвертый квадранты, и части оси у, лежащей вне окружности. Простой нсточинк мощности т расположен в точке (/, 0), причем /><>. Доказать, что скорость жидкости в точках (а cos 6, asinO) иа граничной полуокружности равна

4/на/* sin 29

a -f/ -2aV*cos2e

Определить, в каких точках границы давление будет наименьшим.

33. Внутрь круга радиуса а с твердой границей поступает вода через центр круга О. Через небольшое отверстие в точке А окружности вода вытекает во внешнюю неограниченную область, также занятую водой. Движение предполагается двумерным. Доказать следующее: 1) асимптоты линий тока проходят через фиксированную точку; 2) касательные в точке О к линии тока и к соответствующей асимптоте одинаково наклонены к линии OA; 3) точка А является двойной точкой линии тока, касательные к которой взаимно перпендикулярны. Начертить одну из линий тока.

34. Внутри круга радиуса а помешен источник мощности m на расстоянии / oi центра и сток такой же мощности расположен в центре. Найтн соответствующий комплексный потенциал и показать, что результирующее воздействие иа гр нииу равно

гярт /

at(a* - f*)

Найти направление этой силы. Как предельный случай получить комплексный потен цнал скоростей, обусловленный диполем, помещенным в центре.

35. Источник помещен в точке (с, с) в области, ограниченной осью х и окружностью х*-\-у*==а*, причем источник находится вне окружности. Показать, что скорость равна

24. Доказать непосредственным расчетом, что радиальная скорость иа круговом цилиндре, обусловленная источником и его отображением, равна нулю.

25. Проверить, что источник и его отображение относительно кругового цилиндра имеют окружность цилиндра в качестве линии тока.

26. Доказать, что в случае источника, расположенного вне кругового цилиндра, уравнение линий тока ф = const имеет вид

(х -Н!, ) {сх+у)-{хг+у^ с (l+V)+a* ( -j/) = 0,

где c=tg(/m); =о .

27. В примере 26 доказать, что:

(1) асимптотой линий тока является прямая cx-\-y-c(l-\-l)=Q\,

(2) все асимптоты проходят через точку (f+f, 0);

(3) каждой линии тока внутри цилиндра соответствует замкнутая кривая. Целиком лежащая внутри цилиндра.

28. Доказать, что прн наличии источника в точке А вне круглого диска скорость обтекания на окружности диска наибольшая в точках, где окружность пересекается линиями, соединяющими точку А с коьцами диаметра, перпендикулярного к линии OA. Доказать также, что величина этой скорости равна а* О-центр окружности диска, а-радиус этой окружности.

29. Пусть ось у и окружность х*-\-у*=а* являются неподвижными границами. Пусть в точке (с, 0), причем с>а, находится двумерный источник. Показать, что радиус, проведенный из начала координат до той точки окружности, где скорость максимальна, составляет с осью х угол, равный

в -(-с arccos ----

примеры Ш

нулю в точках (± а, 0) и что она будет обращаться в нуль еще в одной точке на окружности, если 2с<(2+У2)а.

36. Граница полубесконечной жидкости состоит из неограничен ной плоскости, на которой помещен цилиндрический выступ с поперечным сечением в виде полуокружности радиуса а; в жидкости помещена лииия источников на расстоянии с от плоскости и от оси выступа, причем c=atgX,. Показать, что в точках на поверхности выступа скорости достигают наибольшей величины вдоль образующих, лежащих в осевых плоскостях, которые составляют угол 6 с осевой плоскостью. Последняя содержит линию источников, задаваемую уравнением tge=cos2X.

37. Показать, что комплексный потенциал

а =m In {(2-zi) (2-2г)/2}.

где 22:2]-действительное число, задает движение жидкости, соответствующее двумерному стоку мощности ffl, расположенному в точке 2=Z прн наличии неподвижного аилнндра с центром в начале координат н с радиусом а, причем a*=2i22l. Применяя преобразование

2 = 2-Ьс /2. (c<a<l2,),

получить решение для движения жидкости, обусловленного наличием стока вне неподвижного эллипса, и найти результирующую силу давления, действующего на эллипс.

38. Источники равной мощности т расположены в точках г=Ша; при этом п принимает значения

п = ..., -2, -I, О, I, 2, 3,

Доказать, что соответствующий комплексный потенциал равен

w= -т In sh (яг/а).

Исходя из этого показать, что комплексный потенциал диполей с осями, параллельными оси X, и моментами расположенными в тех же точках, задается формулой

=icth (яг/а).

39. Если последовательность диполей, рассмотренная в примере 38, расположена в равномерном потоке, имеющем скорость -U, параллельную оси х, то доказать, что лииия тока 1(1=0 удовлетворяет уравнению

оу sin (2яу/о) я6 ch (2ЯХ/0) - cos (2яу/а)

Показать, что эта лииия состоит из части оси х и из овальной кривой, близкой к окружности (диаметра 2Ь), если величина b мала по сравнению с величиной а. Показать, что полученный результат дает решение задачи обтекания последовательности ровноотстоя-оих параллельных прсфилсй, близких к круговым.

40. Доказать или проверить, что комплексный потенциал, задаваемый формулой

имеет в качестве линий тока 1=тя прямые, выходящие из начала координат. Доказать, что поток втекает в начало координат под одним углом, а вытекает под другим.

41. Пусть ю = /(2) и v=-<fe/d . Показать, что точки v и в являются точками инверсии иа векторной диаграмме. Показать, что если v можно определить как функци от а , то

V dw.

Доказать, что предположение о наличии в плоскости v источника с комплексным потенциалом

aU, / I \ , aU, I

приводит к формуле

=-+f->(-S)-

Доказать также, что определяемый отсюда комплексный потенциал задает течение воды иа открытого пространства в канал ширины 2а, причем скорость внутри канала в бесконечности равна и.

41. Исследовать результаты примера 41 для доказательства того, что комплексный потенциал течения, имеющего скорость U в бесконечности н вытекающего из устья кана-

ла бесконечной длины и ширины 2а, имеет вид

яг nw , , nw

43. Две бесконечные плоскости сходятся под углом 2а=2пп, но они не пересекаются, а образуют насадок, через который течет жидкость. Показать, что соответствующая векторная диаграмма в плоскости v{v=-dz/dw) соответствует диаграмме, рассмо-трениной в примере 40, и вывести, что для течения в насадке выполняется соотношение

Положив C=m/(nU), показать, что отсюда можно вывести результаты примера 42.

44. Пусть жидкость движется внутри тонкой оболочки, состоящей из двух плоских пластинок. Показать, что соответствующее движение внутри тонкой сферичесюй оболочки можно получить путем инверсии линий тока первого движения относительно некоторого центра; определить множитель, на который нужно помножить скорости первого движения, чтобы преобразовать одно движение в другое.

Одинаковые по мощности источник и сток помещены в двух точках тонкой сферической оболочки. Показать, что линиями тока и равного тютеициала на сфере будут малые окружности.

Глава 9 ДВИЖЕНИЕ ЦИЛИНДРОВ

9.10. Кинетическая энергия ациклического безвихревого движения.

Рассмотрим двумерное ациклическое безвихревое движение жидкости, ограниченной изнутри цилиндром Си а снаружи цилиндром Сг (рис. 160). Слой жидкости имеет единичную толщину, т. е. жидкость расположена между двумя плоскостями, параллельными плоскостям течения и отстоящими друг от друга на единицу длины. Из теоремы (1) п. 3.77 следует, что, для того чтобы такое течение существовало, один или оба цилиндра должны двигаться.

Если обозначить область, ограниченную кривыми Ci и Сг, через S, то выражение для кинетической энергии жидкости в данном случае имеет вид

(S) (s)

Использовав теорему Стокса в комплексной форме (см. п. 5. 43), мы получим соотношение

(Ci) (Сг)

в котором оба контура интегрирования обходятся против часовой стрелки.

9.11. Кинетическая энергия циклического движения. Рассмотрим циклическое безвихревое движение жидкости, заключенной в двусвязной области между неподвижными цилиндрами Ci и Сг-

Рис. 160.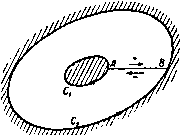

Рнс. 161.

Обозначим через а о комплексный потенциал. По предположению, существует циркуляция интенсивности х, поэтому при обходе контура Ci против часовой стрелки функция а о уменьшается до величины а о -2ях.

Проведем мысленно перегородку АВ между цилиндрами, превратив таким образом область, занятую жидкостью, в односвязную (рис. 161). Перегородка АВ является лишь геометрическим понятием и не влияет на движение жидкости; это будет иметь место в том случае, если АВ состоит

все время из одних и тех же частиц жидкости. Перегородка позволяет образовать односвязную область, в которой функция Шо является однозначной.

Обозначим через С контур Ct + BA + Ci + AB, где кривая С, обходится против часовой стрелки, а кривая Ci по часовой стрелке. Так как Шо = = Шо-2 ф и, следовательно, dwo = dWo - 2id, то кинетическую энергию жидкости можно записать в виде

(C) (C) (C)

Функция Wq является однозначной в области, ограниченной контуром С, поэтому первый интеграл вследствие теоремы Коши обращается в нуль. Так как функция фо постоянна на линиях тока Ct и С то последний интеграл сводится к интегралу вдоль кривой АВ + В А. На дуге АВ комплексный потенциал имеет значение Wo, а на дуге ВА он имеет значение щ - - 2ях. Следовательно,

= Т в S 0 Фо + уQ 5 {Wo - 2ях) йфо = nxQ [(фо)й - (фо)л1, (2)

где (фо)в н (Фо)а - значения функции фо в точках В н А. Таким образом,

Го=яхвт, (3)

где т - расход жидкости, протекающей справа налево через перегородку АВ. Из формулы (3) следует также, что

Г, = -5 в 5 2ях-Й5= С nxc9 ds, (4)

.где 9 -составляющая гкорости, нормальная к перегородке АВ. Последнее выражение представляет собой работу, совершенную импульсивным давлением величины 2яхо, приложенным к перегородке АВ, если жидкость первоначально покоилась.

Таким образом, данное циклическое движение могло бы возникнуть из состояния покоя под действием импульса 2ях(}, приложенного к перегородке, если предположить, что перегородка немедленно исчезает после приложения импульса. Обратно, если установилось циклическое движение, жидкость можно было бы привести в состояние покоя путем приложения импульсивного давления противоположного знака к перегородке, подобной АВ. Отсюда следует, что циклическое движение не может быть создано или остановлено импульсивным давлением, приложенным только к границам Ci и Cj.

Итак, мы можем обобщить теорему II п. 3.77 следующим образом (по крайней мере для двумерного движения).

Если жидкость, занимающая двусвязную область, ограниченную твердыми стенками, совершает ациклическое движение, то движение мгновенно прекращается, если границы приводятся в состояние покоя. Однако ест движение является циклическим, то циклическая часть будет сохраняться при остановке границ.

Теорема VI допускает подобное же обобщение. И вообще, если задана интенсивность циркуляции, то безвихревое движение в двусвязной области полностью определено.

Эти теоремы, доказанные здесь для случая двумерных двусвязных областей, приложимы к областям любой связности в трехмерном пространстве.