плоскости JC = О и отображенная система S состоит из источника в точке В (рис. 149).

Заметим, что точка В является оптическим отражением точки А относительно данной плоскости, рассматриваемой как отражающая поверхность.

8.41. Действие на стенку точечного источника. Пусть источник находится в точке А (а, 0), а стенка представляет собой плоскость х = 0. Отображением источника относительно стенки является источник той же мощности, расположенной в точке В (-0,0), и, следовательно,

w= -т1п{г - а) - т\п{г + а)= -m\n{z* - a*),

dw - 2тг ~d~z~ z*-a*

На стенке х = 0, и поэтому

dw -2mty dw 2miy dz ~ -yi-a* -yt-at

отсюда находим

Ч {yt+ai)i

где g -скорость, направленная вдоль стенки, которая является линией тока. Следовательно, давление на стенку задается формулой

jn 1 а П 2т уД

Q - С 2 - Q {у*+а*)*

где П -давление в бесконечности.

Если жидкость находится в покое, то давление повсюду равно П. Таким образом, эффект движения состоит в уменьшении давления на стенку. Следовательно, стенка действует на источник с силой (на единицу ширины стенки), определяемой формулой

Полагая y = atg6 (рис. 150), из формулы (1) мы получим, что на стенке имеет место выражение

=f-T 2e. РИС. i50.

так что наибольшая скорость на стенке достигается при 6 = ± я/4.

8.42. Общий метод отображений относительно плоскости. Мы можем поступать почти так же, как в случае теоремы о круге, рассмотренной в п. 6.21. Так, если функция

f(z)= -2т,1п(г-гг)

является комплексным потенциалом источников и стоков, которые находятся в полуплоскости у>0, то наличие плоского барьера вдоль прямой у = О приводит к комплексному потенциалу вида

w = f(z)+f (г) = - 2тг In (г - 2,) - Znir In (г - 2,),

- 2ят = J йф = J йф.

(О (V)

Мы можем брать окружность с сколь угодно малой, и кривая у также будет уменьшаться, ио интеграл от йф вдоль кривой у будет оставаться постоянным и, следовательно, в точке П имеется источник. Если кривая у охватывает точку П только один раз (обычный случай), то источники в обеих плоскостях будут одинаковой мощности.

поскольку при у = О мы имеем г = 2, так что w действительно и у=0 является линией тока tp = 0. Кроме того, если точки Zr лежат в области у >0, то точки Zr расположены в области у < О, так что этот прием ие вводит новых особенностей в область у>0.

Аналогично, если все источники и стоки лежат в полуплоскости х>0, то наличие плоского барьера вдоль прямой х = 0 приводит к комплексному потенциалу вида

w= f{z)+]( - z) = - Lnir In (г-Zr) - 2шг In ( - z-Zr),

так как здесь при ж = 0 мы имеем -z = г и t)=0. Этот метод также применим к прямолинейным вихрям (гл. 13).

8.43. Отображение диполя относительно плоскости. Если взять двумерный диполь с моментом наклоненный под углом а к оси х, то его можно

рассматривать как предельный случай стока в точке А и источника в точке В, причем прямая АВ образует угол а с осью х.

Отображениями источника и стока яв-

/g ляются точки В' и А'; они получаются как

x оптические отражения точек В н А относи- тельно оси у, представляющей данную пло-

скость. Переходя к пределу при А-В, мы имеем А'->В', и, следовательно, отображение представляет собой диполь с моментом Р (1, ось которого образует с осью х угол

я -а (рис. 151).

Используя метод п. 8.42, мы имеем для изолированного диполя в точке Zq комплексный потенциал /(z) = ie**/(2 -Zo), и, следовательно, при наличии плоскости л: = 0 получаем

W= -1---* - .

8.50. Источники при конформном преобразовании. Если отобразить плоскость Z на плоскость с помощью конформного преобразования

C=f(2),

то источник в плоскости 2 преобразуется в источник в соответствующей точке плоскости С-

Доказательство. Пусть имеется источник мощности т в точке Р с координатой г = Zo в плоскости z и пусть точка П с координатой С = Со в плоскости I соответствует точке Р. Проведем малую окружность с с центром в точке Zo, и пусть у -кривая в плоскости Ci соответствующая этой окружности. Эта кривая у должна окружать точку П.

Поскольку функция тока ф имеет одинаковое значение в соответствующих точках обеих плоскостей, то

Если кривая у охватывает п раз точку П, когда окружность с охватывает точку Р один раз, то источник в точке П имеет мощность т/п.

Для примера предположим, что C=z и что в точке г = 0 имеется источник мощности т.

Так как

arg С = 3 arg г,

то, когда величина arg г увеличивается на 2п, величина argj увеличивается на 6л и, следовательно, кривая у будет охватывать точку С = 0 три раза. Таким о(5разом, в точке 1=0 имеется источник мощности т/3. С другой стороны, если C = z, то кривая у охватывает точку i = 0 один раз, когда окружность с охватывает точку г=0 три раза; поэтому в точке t, = 0 имеется источник мощности Зт.

8.51. Источник, расположенный в углу между двумя стенками. Пусть источник мощности т находится в точке Zo между двумя стенками, накло-

л I

г-плослость С-ллос/юсло Чо

Рис. 152.

ненными друг к другу под углом л/п, и пусть одна стенка совпадает с осью х (рис. 152).

Рассмотрим преобразование

С = г ,

тогда

arg С = п arg г,

и, следовательно, когда величина arg г увеличивается от О до л/п, величина arg увеличивается от О до л, а внутренняя область угла отображается на верхнюю половину плоскости С-

Источнику в точке Zo соответствует равный по мощности источник в точке

Со = 2?.

Отображением этого источника является равный по мощности источник в точке to. и, следовательно, комплексный потенциал источника вместе с еги отображением выразится в виде

w= -mln(C-W-nln(C-Co).

Таким образом, в плоскости z имеем

w= - т1п(г -zj) -mln(z -zy).

8.60. Источник вне кругового цилиндра. Пусть в точке z = f, где /-действительная величина, имеется источник мощности т, расположенный вне цилиндра радиуса а с центром в начале координат. Если источник один, то комплексный потенциал равен - m 1п (z - /). Если цилиндр поместить

в поток, то, согласно теореме об окружности (см. п. 6.21), получим следующий потенциал:

)= -mln(z-f)-mln(y -/) .

8.61. Отображение источника, расположенного вне кругового цилиндра.

Если к комплексному потенциалу из предыдущего пункта добавить константу

/п1п(-1 ), то получим потенциал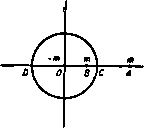

- /nln{z-f)-/n\n -У } +fnlm.

Этот комплексный потенциал (рис. 153) дает:

1) источник мощности т в точке А, z = f;

2) источник мощности т в точке В, z = a*/f;

3) сток мощности -m в начале координат. Так как ОАОВ= а', то точки А и В являются

инверсиями относительно кругового сечения цилиндра и, следовательно, точка В находится внутри цилиндра.

Таким образом, отображение источника, расположенного вне кругового цилиндра, дает систему, состоящую из одинакового по мощности источника

Рис. 153.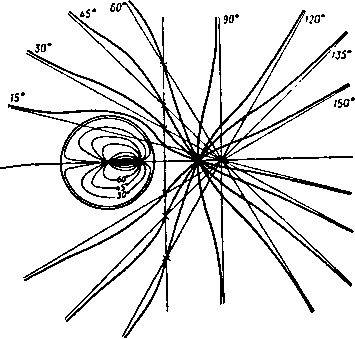

Рис. 154.

в точке инверсии и равного по мощности стока в центре цилиндра. Линии тока изображены на рис. 154. Отсюда следует, что источник внутри цилиндра и равный по мощности сток в центре цилиндра имеют в качестве отраженной системы равный по мощности источник в точке инверсии данного источника. Скорость в любой точке Р дается формулой

I dw

т

(г-Пг(г-а*/П

= т

РСРр РАРОРВ

где С и D -точки, в которых прямая АВ пересекает окружность.

Если точка Р находится на окружности, то треугольники ОВР нОРА подобны и поэтому

PB:PA=a:f.

8.62. Сила, действующая на круговой цилиндр от источника. Если взять, как это показано на рис. 153, обтекаемый цилиндр с источником в точке А на оси х, то по теореме Чаплыгина -Блазиуса имеем

где интеграл берется по контуру цилиндра. Теперь заметим, что w-m\nz-m ln(z - f)-mIn(z -/).

где

0Л = /, ов=г = ,

dw tn ftt ftt

Возводя в квадрат последнее соотношение и выражая результат в виде суммы дробей, получаем

(dw \* т* . т* т* 2т* 2т* ,

dx J - г*- (г-Пг (x-f)* г/ Цх~П +

2д| 2т* 2д| 2т

(z-f){f-n (z-nU-f) гГ (г-ПГ

Внутри контура имеются такие полюсы: z = О, z=f, следовательно, сумма вычетов равна

2т* 2т* 2т* 2т* 2m*f 2т*а* I r-t г г ~ fU-f) ~ f(a*-P)

Поэтому

f(a*-f*)

V п V 2пдт*а*

Следовательно, результирующая сила притягивает цилиндр к источнику. Исследование линий тока показывает, что давление имеет большее значение со стороны, наиболее удаленной от источника. То же самое верно для стока.

8.63. Теорема Лагалли. Рассмотрим равномерный поток и источник; комплексный потенциал для потока с компонентами скорости (-U, -V) в бесконечности и при наличии источника мощности т в точке г = а имеет вид

(i;-/V)z-m in(z-a).

Если в поток поместить цилиндр, то комплексный потенциал изменится из-за добавления функции, которая должна равняться нулю в бесконечности, так как присутствие цилиндра не может оказывать воздействия на удаленные части жидкости. Для общности предположим, что вокруг цилиндра имеет место циркуляция х. Тогда полный комплексный потенциал на достаточно большом расстоянии от цилиндра имеет вид

a) = ((/-iy)z-mln{z-a) + /ifelnz-f4 + --+---

Причем последние члены выражают наличие циркуляции и возмущение вносимое цилиндром.

Комплексную скорость запишем следующим образом:

Для нахождения силы, действующей на цилиндр, по теореме Чаплыгина - Блазиуса имеем

-у-Ц (

Пусть 5 -окружность большого радиуса, содержащая внутри себя цилиндр и источник (рис. 155). По методу п. 5.54 мы можем расширить контур цилиндра до S и, таким образом, написать

(8) (с) (v)

где у-малый контур, проведенный вокруг источника. Поэтому находим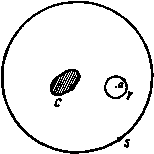

X-iY

(8) (V)

Рис. 155.

Далее, на окружности S в силу того, что \г\ велик, мы можем разложить l/(z -а) по степеням 1/г. Следовательно, из формулы (2) получим

а отсюда

iQ I (ydz - 2nQ (U - iV) (/n - ix).

где A, B,... - некоторые константы. Таким образом яо теореме о вычетах находим

Для вычисления второго интеграла в формуле (3) мы заметим, что, согласно формуле (2),

-=Мг) + 7.

где

Мг)= --[w-{-m\n(z-a))].

Следовательно, функция / (г) представляет собой комплексную скорость, полученную при исключении источника из первоначального комплексного потенциала; функция f(z) аналитична внутри контура у. Далее имеем

По теореме Тейлора находим

f{z)fl{z-a)+a]f{a) + {2~a)r(a) + ....

Неяшмнят и owwat til

Огазда ычет шражения (- в точке г -а равен 2mf{a). Исоояьвуа еще раз теорему о вычетах, нз формул (3) и (4) получаем

X -/У - 2яв ((/- У) (т - ix) + 2>1в /(а)-

~-2яQiк^U-iV) + 2яvn(U-iV + fa)). (б)

Здесь величина / (а) является комплексной скоростью в точке а, снаду-онроваииой той частью комплексного потенциала, которая остается оосяе удаления источника мощности т. Таким образом, обозначая ату сиидушн рованнук скорость через и. -мы окончательно получаем

X-ZK- 23i9in(U-iV) + 2 vn(U-iV+u -io). (7)

Эта формула выражает теорему Лагалли, которую можно распространять на любое число источников, добавляя каждый раз член такого же вида, как последний член в формуле (7). Чтобы найти соответствующее выражение для момента М, имеем

Вычислив вычеты по предыдущей формуле, получим

М-\ iN-ш -tt9il(m-in)*-m*-2(U-iV){A + ma)-2amf(a)]

- 2яА {U-iV) + xQix(x + 2im) + TuQima (U-iV + u-/о.). (8)

Момент Af является дейстштельноА частью этого выражения. Теорема Лагалли принимает ннтересиую форму в случае, когда поток и luipKyxiun отсутствуют, так что поле источника находятся только один шитдр. В этом случае формула (7) принимает вид

X-f У-2явт(н,-Ц|>,). (9)

в то время как выражение, определяющее момент

Af -f iW 2nQima (и - /v.).

показывает, что Af является моментом силы (X, Y). действующей в точке о. Следовательно, на цилиндр действует сила (X. К) по линии, проходящей через источник и в том же направлении, что и скорость, нидуциропниаа а источнике.

Таким образом, мы получили следующую теорему.

Теорема. Источник мощности т при наличии цилиндрадейетвцет на цилиндр с комплексной силой 2xQin (и Ч-/о.), линиш действия которой проходит через источник, где u + iv-KOsuueKCHOM скорость, индицированном той частью комплексного потенциала, которая остается после удаления источника.

Когда имеется несколько источников, то каждому нз них соответст-ует своя сила (9) со своей линией действия ). Эту теорему мы можем применить сразу же для нахождения силы, действующей на круглый цилиндр от источника.

Таким образом, в обозначениях п. 8.62 имеем

w = m\m-m 1п(г -/) -m In (г - /).

Отсюда находим

т , т то*

и- -ip- - - у { - .

М Соогктстиуюшаа Tptncpua теорема машметса в в. I&.42.

следовательно,

X-iY=

как это уже было получено ранее.

2 gm a

8.64. Источник вне эллиптического цилиндра. В п. 6.31 преобразование Жуковского было использовано для получения потока вокруг эллиптического цилиндра, после того как был получен соответствующий поток вокруг кругового цилиндра. Подобным же образом комплексный потенциал, обусловленный источником вне кругового цилиндра, может быть использован для получения комплексного потенциала источника вне эллиптического цилиндра. Рассмотрим круговой цилиндр радиуса {а+Ь)/2 с источником в точке Zp. Тогда в плоскости Z имеем

ш= -l-mlnZ-/nln(Z-Ze)-/nln(Z-Z;), где Zj-инверсия точки Zg, и, следовательно, если

Zp = re ,

то мы получим

с помощью преобразования п. 6.31

мы получим комплексный потенциал для источника мощности т в точке Zp при наличии в потоке эллиптического цилиндра с полуосями а н Ь.

8.70. Отображение иа единичный круг. Рассмотрим в плоскости Z круг единичного радиуса с центром в начале координат. Координаты любой точки окружности этого круга можно представить в форме XcosQ,

г-пйосность

Рис. 156.

У = sin 9. Так как угол 9 увеличивается от О до 2я, то точка (X, Y) описывает окружность в направлении против часовой стрелки. Поскольку мы будем рассматривать область вне этой окружности, то удобно написать 0=-, так что при увеличении 5 от О до 2п точка (л, У) описывает окружность по часовой стрелке и, следовательно, область, внешняя по отношению к окружности, остается слева (рис. 156). Таким образом, каждая точка окружности может быть выражена в виде

Z = X-b/K = cos5-/sin = e- . (1)

Если координаты точки заданной кривой можно представить в виде z = ape- -l-6p-l-M -l-6te2 -l-.... (2)

где кривая описывается по часовой стрелке при увеличении £ от О до 2л, то область, внешняя относительно данной кривой, отображается на область, внешнюю относительно единичного круга, с помощью формулы

2 = f(Z) = fl,Z-l-6p + - + +.... (3)

Этот результат получается путем исключения из формул (1) и (2). так как направления обхода кривых одинаковы.

Например, в случае эллипса с полуосями (а, 6) мы имеем

Z = а cos 6 - ib sin 5 -1 (а + b) +(а - b) е% (4)

так что требуемое отображение

z = Z + (5)

является преобразованием Жуковского.

Семейство кривых, обладающих этим свойством, было изучено Рничем *); оно описывается уравнением

г=-ф-е- +-е* +бе 1. 0<Ь<а. (6)

Рассматриваемые кривые отображаются на единичную окружность IZI = 1 с помощью формулы

2=42+-+-. (7)

которую следует сравнить с формулой (5).

Это семейство состоит из кривых, начиная от гипоциклоид с тремя точками возврата, если а= 6, и кончая симметричными профилями крыльев, если 6<ViO.

8.71. Источники вне цилнщра. Пусть область в плоскости г, внешняя относительно кривой С. отображается на область, внешнюю относительно окружности Zf=l в плоскости Z, с помощью функции

z=f(Z). (1)

Если в рассматриваемой области вне кривой С в плоскости г имеется источник мощности т в точке Zo. то в соответствующей точке Z вие окружности имеется источник мощности т и, следовательно, по теореме об окружности имеем

а =-/nln(2-Zq)-mln(--Z,) , (2)

что вместе с формулой (1) определяет комплексный потенциал w в плоскости Z.

В случае диполя имеем, как в п. 8.23,

/п -mfiZo- ln(Z-Zo)-m6Z,-ln Q-Zo .

) Wrinch D., Phil. Mag. (6), 48(1924).

Далее, если положим (ic°=m6zo, то из формулы (1) получим таким образом.

(Z-:zo)/(Zn) (i-2Zo)7(Zo)

8.72. Сила, действующая на цилиндр. Воспользуемся теоремой Дагалли из п. 8.63, согласно которой

Х - Г = 2п(уп (ы„ -

где индуцированная скорость вычисляется путем отбрасывания источника в комплексном потенциале. Таким образом, Um -iVm= F (Zo)> где F(z) = = -w-mln{2-2o): z={{Z).

Следовательно, воспользовавшись формулой (2) п. 8.71, получим

F (г) = m In (2-Zo) 4 m In f Z - 4Л - m InZ-m In{/ (Z) - / (Z,)j. Таким образом, имеем

Um-lVm =

mf (Z) mZo

Z-Zo l{Z)-l(Zo) zZo-l Z Воспользуемся разложением в ряд Тейлора,

/ (Z) = / (Zo) Ч- (Z - Zo) / (Z,) + J- (Z - Zo) r (Zo) Ч ...,

откуда после приведения к одному знаменателю получим

~ / (Zo) I 2/ (Zo) + z (2oZo-1) J

По теореме, доказанной в п. 8.63, линия действия этой силы проходит через точку Zo. так что нет необходимости отдельно вычислять момент этой силы.

Простой иллкхгтрацией этого результата является применение к эллиптическому цилиндру, отображение которого дается преобразованием Жуковского (5) п. 8.70. Анализ этого случая предлагается выполнить в качестве упражнения.

8.80. Источник и сток вне кругового цилиндра. Рассмотрим сток мощности т в точке S, и равный с ним по мощности источник в точке 5 . оба расположенные вне кругового цилиндра с центром О. Если SJ и 5 - точки инверсии, то отображенная относительно окружности система состоит из стока мощности - m в точке SJ, источника мощности т в точке О, источника мощности т в точке 5 и стока мощности - m в точке О. Она сводится к стоку мощности - m в точке S. и источнику мощности m в точке 5, так как источник и сток в точке О нейтрализуют друг друга.

Поскольку

OSrOS[ = a* = OStOS

точки Si, St, 5j, являются циклически сопряженными.

Так как линиями тока для источника и равного по мощности стока являются окружности, то окружность, проходящая через вышеуказанные четыре точки, является линией тока. Следовательно, окружности пересекаются в критических точках А н В.