а

г' = -1-\-ае* выражается формулой Af = 2neW sin 2а.

II. Показать, что внешность окружности 2 = а в плоскости Z преобразуется во внешность дуги круга на плоскости г с помощью конформного отображения, определяемого соотношением

г-ое2< Z-ffl у.

г аг-2<а \ z+iae- У

при этом дуга круга имеет центральный угол, равный 4а. Показать также, что отношение г/2 стремится к sin а в бесконечности.

Цилиндр, поперечным сечением которого является рассматриваемая здесь дуга круга, помещен в поток, имеющий в бесконечности скорость V. Скорость V перпендикулярна к образующим цилиндра и составляет положительный угол § с радиусом, соединяющим центр круга с серединой дуги. Кроме того, вокруг цилиндра имеет место положительная циркуляция X. Показать, что соответствующий комплексный потенциал w можно получить, исключая переменное Z из предыдущего соотношения и следующего уравиения:

w= -V sin а

Доказать, что скорость у верхней кромки будет конечной тогда и только тогда, когда

x = 2naV (sin P-l-sin (2а-р)1.

12. Окружность lt = e отображается на профиль в плоскости г с помощью преобразования 2= (4-а*, Доказать, что в окрестности точки г = 2а справед.1иво разложение

icHHTb построение, приведенное в п. i.oi, для вычерчивания профилен, окружностей, проходящих через заданную точку В. Центры окружностей оответственно в точках 1/10 е* *, 10 е* /. Измерить в каждом случае

dz 2 yjH

13. Для профиля Жуковского, изображенного на рис. 131, показать, что центр окружности расположен в точке se*, а длина хорды 17* выражается формулой

4s* cos* ц

г-/2$со$ц

Показать, что для тонких профилей малой кривизны длина хорды приближенно равна 4а.

14. Применить построение, приведенное в п. 7.31, для вычерчивания профилей, получаемых нз расположены соответственно относительную кривизну н толщину.

15. Окружность 1С 1 = 0 в плоскости I преобразуется в тонкий профиль крыла на п.юскостн г с помощью формул

г' = 11+ А„1ат An = Bn+iCn, г=г'+ЬЧг',

где b - действительное число, мало отличающееся от величины а, причем величина 6 выбрана так, что для z = -b соответствующая точка в плоскости лежит на окружности; постоянные величины В„ и С„ малы. Найти зависимость толщины профиля и ординаты его кредней линии от величин В„, С„.

Лока1ать. что если циркуляция выбрана из условия конечности скорости на задней кромке, то коэффициент подъемной силы профиля равен С^ = 2л (a-f-X). При этом угол атаки а считается малым, а величина к выражается в виде

n=l о

rje у -ордината средней лнинн, равная величине 26 cos 6 и отсчитываемая от середины .динни. соединяющей переднюю кромку с задней.

Кроме того, показать, что коэффициент момента относительно передней кромки приближенно равен /4Сь + /2яХ. -/iCj. Показать также, что если коэффициент момента обращается в нуль вместе с подъемной силой, то центр давлений расположен на расстоянии четверти длины хорды от передней кромки для всех малых значений угла атаки.

Тогда показать, что скорость потока направлена по касательной в точке возврата и имеет величину (а+Р) показать, что момент сил давления М относительно точки

Глава 8 ИСТОЧНИКИ и СТОКИ

8.10. Двумерный источник. Определение. Если двумерное движение жидкости представляет собой течение жидкости от какой-либо точки по радиусам симметрично во всех направлениях координатной плоскости, то эта точка называется простым источником (рис. 140, 141).

Рис. 140. Рис. 141.

Двумерный источник можно рассматривать как прямую ось (единичной длины между двумя фиксированными плоскостями), из которой вытекает жидкость описанным выше образом.

Определение. Если 2пт есть полное количество жидкости, вытекающей в единицу времени, то т называется мощностью источника^).

Источник является чисто абстрактным понятием; таких источников в действительности не существует. Тем не менее это понятие оказывается полезным, так как многие движения жидкости можно описать, считая их обусловленными источниками, расположенными вне области, занятой жидкостью. Источник, таким образом, является точкой, в которой жидкость непрерывно образуется и вытекает. Так как скорость вблизи источника очень велика, то по теореме Бернулли давление должно быть большой отрицательной величиной.

Один этот факт показывает, что источник в вышеуказанном смысле не может физически существовать. Однако расширяющийся пузырек газа отталкивает окружающую жидкость и, таким образом, приближенно имитирует источник. Если мощность источника с течением времени не изменяется, то источник называется установившижя.

Определение. Стоком называется отрицательный источник. Таким образом, сток - это точка, в которую радиально втекает поток и в которой жидкость непрерывно поглощается.

Если Up - радиальная скорость на расстоянии г от источника, то полное количество жидкости, вытекающее в единицу времени через окружность радиуса г, равно

2яг г = 2пт. Таким образом, т

) Некоторые авторы обозначают через m объемный расход. Тогда мощность равна т/2л. Цель настоящего обозначения состоит в том, чтобы избежать повторения множителя 2л в последующем исследовании (ср. интенсивность циркуляции в п. 7.10).

это выражение представляет собой полную скорость для изолированного источника.

8.1Й. Комплексный потенциал для простого источника. Если источник мощности m находится в начале координат, то радиальная скорость в точке с координатами (г, Q) равна т/г Следовательно,

- = ы -/ =-у-(cos в -1 sin в) =, w= -minx. Функция тока имеет вид ф = -тв.

Если источник находится в точке Zo, то, перенося в нее начало координат, получаем

w= -т\п{г-гщ).

Интересно сравнить этот результат с комплексным потенциалом для вихря интенсивности х, данным в п. 13.21. Математически вихрь является источником с мнимой мощностью.

Следует заметить, что с увеличением радиуса г скорость уменьшается, так что на большом расстоянии от источника жидкость почти иеподиижиа.

Характерным для источника (или стока) является то, что скорость стремится к бесконечности, кргда мы приближаемся к источнику, и, следовательно, в непосредственной близости от источника скорость всегда радиальна, как бы жидкость ни двигалась в далеких точках.

8.20. Комбинация источника н стока. Движения, обусловленные равномерным потоком и любым числт источников, можно получить сложением соответствующих комплексных потенциалов, если жидкость безгранична.

Для доказательства рассмотрим комплексный потенциал

ю= -f/z -ntilnz-miln( -Zt).

Покажем, что этот потенциал задает равномерный поток в бесконечности и источники мощности mi, mt в точках 2-0, z=Zo-Так как

-< =-- + ?+7.

то при z-*oo получаем u=U, о=0, так что имеется равномерный поток. С другой стороны, в окрестности точки z=2 положим z = Zo+re*; здесь г мало. Тогда

Первые два члена в правой части этого соотншпення малы по сравнению с третьим, следовательно.

ы = -со8в. oesinO,

так что в точке Zq имеется направленный наружу радиальный поток, обус.ювленный источником мощности т, в этой точке.

Таким же путем доказывается, что в начале координат имеется источник мощности mi. Это доказательство может быть распространено на любое число источников и стоков.

Мы намеренно доказали свойство аддитивности потоков, так как оно не очевидно для источников и вообще не выполнимо в других случаях.

Например, обтекание кругового цилиндра с центром в начале координат задается комплексным потенциалом

Движение, обусловленное источником в точке Zq, задается функцией - mln(z -Zo).

Если оба эти потенциала сложить, то получим

f/(z + -)-mln(2-Zo).

Эта функция является комплексным потенциалом некоторого движения, но не соответствует обтеканию цилиндра при наличии источника. Нарушение свойства аддитивности здесь очевидно, так как функция тока не равна постоянной величине на окружности г=а, поэтому цилиндр не является линией тока.

8.21. Источник в равномерном потоке. Рассмотрим комбинацию источника мощности ш, расположенного в начале координат, и равномерного потока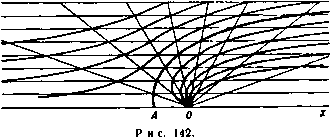

скорости и, параллельного оси х. Тогда, сложив соответствующие потенциалы (п. 8.20), получим

ш= -Uz - mlnz, dw

Здесь z=-mlU является единственной критической точкой. Она расположена на действительной оси в точке, где скорость потока и скорость, обусловленная источником, уничтожают друг друга. Функция тока имеет вид

ф= -i/y -marctg= -Uy - mQ;

линии тока легко провести по методу Рэнкина, как показано на рис. 142.

Мы видим, что линии тока симметричны относительно оси х, через которую нет потока жидкости. Разветвляющаяся линия тока проходит через критическую точку А и делит поток на две части. Следовательно, можно предположить, что эта кривая заменена твердой стенкой. Тогда функция тока (1) задает возмущение в равномерном потоке, обусловленное присутствием этой стенки; источник расположен вне жидкости, и, таким образом, мы получили представление действительного движения жидкости.

Рассмотрим часть потока, для которой у>0. Если мы будем отсчитывать угол 0 против часовой стрелки от нулевого значения для точек, находящихся на положительной части оси х, то на отрицательной части оси X имеем у = 0 и 0 = я. Следовательно, для этой части потока

формула (1) дает ф - тя и разветвляющаяся линия тока имеет уравнение

- тя= -Uy-mQ.

Она включает стенку и отрицательную часть оси х. Далее, y-mn/U = h при 6- О, следовательно, имеется асимптота y = h (рис. 143). В силу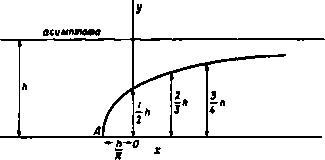

Рис. 143.

симметрии имеется вторая асимптота у = -h. Тогда из формулы (1) находим уравнение стенки в виде

l= ltg

яу

у ° А

Например, найдем, что x t = 31,9 при у/А = 0,99. Полученный результат допускает некоторые интересные физические интерпретации.

Мы можем рассматривать соотношение (1) как функцию тока для потока в окрестности одного конца длинного затупленного тела, обращенного передней частью к потоку, например длинный остров в широкой реке.

С другой стороны, если мы сосредоточим внимание на части кривой выше оси X, то получим картину течения у дна океана; при этом ординаты дна изменяются от О до Л достаточно постепенно.

Эту картину можно также рассматривать как поток ветра, встречающий отвесную скалу. В этой связи интересно отметить, что критическая точка А будет наиболее защищенным местом.

Кроме того, мы можем рассматривать любую линию тока как твердую стенку и тогда получим поток ветра над более пологой поверхностью земли, но здесь уже не имеется критической точки.

8.22. Источник и сток одинаковой мощности. Пусть имеются соответственно источник и сток (каждый мощности т) в точках А н В с аффиксами

ае* , - ог**. Тогда комплексный потенциал имеет вид

ш= - mln(z-аг* )--т1п(г+ав* ),

так что для произвольной точки Р с координатой г функция тока имеет вид

ф=-m.(Z АРВ). Линии тока задаются уравнением ф = const, или /.APB - coxtsX, и, следовательно, они представляют собой соосные окружности, проходящие через точки А н В.

Поток направлен от источника к стоку, так что дуги одной окружности, расположенные по разные стороны линии АВ, описываются в противоположных направлениях. Линия тока, совпадающая с прямой АВ, является предельным случаем окружности. Направление течения на этой линии указано на рис. 144.

8.23. Диполь, или двойной источник. Предположим, что в только что рассмотренном случае течения жидкости точки А и В расположены очень близко друг к двугу, так что а мало. Тогда, используя разложение в ряд функции \n{\ + k), можем записать равенства

y=-mln[z(l--2)]-fmln[z(l +f)] = = ; ,n(l )+; ln(n-) =

2тае

Пусть 2та = ц, тогда

,3ie

Пусть теперь а->0, но величина i остается постоянной, так что т-*оо. Тогда, если точки i4 и fl совпадут, мы получим

Эта комбинация источника и стока бесконечной мощности, находящихся на бесконечно малом расстоянии друг от друга, иазывается диполем

с моментом i. Линиями тока по-прежнему являются окружности (см. рис. 101), имеющие общую касательную, образующую с осью X угол а. Эта общая касательная называется осью диполя, при этом положительным направлением вдоль оси считается направление от стока к источнику. Для лучшего физического понимания диполя можно рассматривать его приближенно как короткую двумерную трубку, в один конец которой жидкость втекает и тотчас же вытекает с другого конца; при этом направление трубки является осью диполя.

Комплексный потенциал можно получить другим путем, который является весьма поучительным. Рассмотрим сток в точке Zo и источник в точке Zo + 6zo; в этом случае имеем

Рис. 144.

- mln(z -Zo -6ze)+mln(z -Zo).

Отсюда можно получить приближенное равенство

w = - m6zo In (г-2о).

Пусть б2о = ге*< . Тогда, если mr = \i н остается константой при/-- О, то мы получаем для комплексного потенциала диполя с моментом ц.

в точке Zo следующее выражение:

W= .

При этом ось диполя имеет направление а.

8.24. Эквивалентный слой диполей по Грину. Рассмотрим безвихревое движение жидкости в области L, ограниченной контуром С (см. рис. 88). Пусть движение жидкости задано комплексным потенциалом w{2), аналитическим во всей области. Это условие исключает особенности и циркуляцию. Тогда по формуле Коши из п. 5.59 имеем

j(,) 0. (1)

смотря по тому, будет ли г внутри или вне области L.

Если ds обозначает элемент дуги С, проведенный в положительном направлении обхода, то мы можем написать d = dse и, следовательно, для точки Z области L формула (1) запишется в виде

(С) (С)

где

fiex = ii (C)e* * b)/(2 ). (3)

Это уравнение определяет действительное положительное число ц и угол Х- Заметим теперь, что <fs/(z-С) является комплексным потенциалом в точке Z для диполя мощности [ids, расположенного в точке ось которого имеет направление %. Следовательно, формула (2) показывает, что комплексный потенциал w{z) можно рассматривать как непрерывное распределение диполей вдоль контура С; при этом плотность распределения на единицу длины дуги дается формулой (3). Это распределение известно как эквивалентный слой диполей по Грину. Относительно другого вида эквивалентного слоя, также данного Грином, см. п. 13.64.

Заметим, что если точка z находится вне области L, то скорость, обусловленная распределением, равна нулю, поскольку, как это видно из формулы (1), w(z) тогда является константой, а именно нулем.

Если область L двусвязная (как на рис. 161), то мы можем сделать ее односвязной, проводя воображаемый барьер АВ. Тогда можно применить предыдущие соображения, если, кроме того, поместить диполи с каждой стороны барьера АВ.

8.30. Источник и сток в равномерном потоке. Пусть имеется источник мощности т в точке А (а, 0), сток мощности т в точке В ( - а, 0) и равномерный поток скорости и, параллельный действительной оси. Интересен случай, когда поток направлен от источника к стоку, т. е. в направлении отрицательных значений х.

Тогда имеем

а =t/z-/я 1 п (Z - а)-f m 1 п (Z-f а). Критические точки определяются из уравнения

И, следовательно, даются формулой

, / , , 2ат г=± уа* + -.

тогда имеем

Пусть

и

г=±Ь,

так что критическими точками являются точки L и М, где 0L = ОМ = Ь. Функция тока имеет вид

ф = {/ / -marctg +m arctg =Uy - maxc\.g-

x-j-fl - + -a

Функция тока ф = О содержит действительную ось у = О и, следовательно, разветвляющаяся линия тока имеет вид

х*-\-у*-а* т После преобразования получаем

x*+y*-a* = 2aycig =2at/ctg- .

Это уравнение представляет кривую, симметричную относительно обеих осей, так как если на ней находится точка с координатами (дс, у), то на

ней также находятся точки (± х, ± у).

Значение у не может быть бесконечным на этой кривой, так как, когда мы удаляемся от АВ, поток становится параллельным оси х. Следовательно, кривая имеет вид замкнутого овала типа, указанного на рис. 145.

Пусть ОН = с, тогда у = с при д: = О и поэтому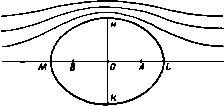

Рис. 145.

c*-a = 2accig

hi -а*

величину с можно найти графически.

Если мы возьмем эту кривую в качестве фиксированной границы, то получим обтекание цилиндра, поперечным сечением которого является вышеупомянутая кривая.

Когда а мало, то приближенно имеем

следовательно.

Таким образом, с-*Ь при а-*О и овал становится окружностью. В этом случае источник и сток образуют диполь и мы снова имеем обтекание кругового цилиндра радиуса Ь. Момент диполя 2am = \i, и, следовательно, имеем

что совпадает с результатом, уже полученным в п. 6.22.

Комплексный потенциал обтекания кругового цилиндра имеет вид

Первый член представляет собой равномерный поток, второй -возмущение, обусл(яленное цилиндром. Таким образом, цилиндр радиуса а, помещенный в поток скорости U, ведет себя как диполь с моментом Ua* на оси цилиндра.

8.31. Два равных по мощности источника. Источники одинаковой мощности т, расположенные в точках А (а, 0), В { - а, 0), характеризуются комплексным потенциалом

w= -т]п(г-а) - т]п(г + а), ff + i=s-mln{x*-y* - a + 2ixy). (1)

2jr/J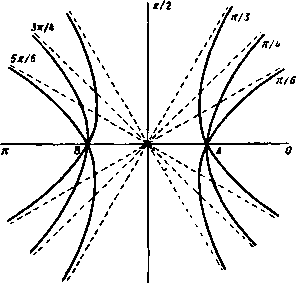

Рис. 146.

Следовательно, функция тока выражается в виде

x + 2xycig -у* = а*.

Таким образом, линиями тока являются равносторонние гиперболы с центрами в начале координат. Это видно, если уравнение (2) записать в форме

Отсюда также видно, что асимптоты, полученные приравниванием нулю каждого множителя, стоящего в левой части, пересекаются под прямыми углами.

Задавая величине ф/(2т) последовательно значения

я я ji 2я Зя 5я

б'432* 34* 6

мы получим картину, представленную на рис. 146, на которой пунктирные линии являются асимптотами.

Оси координат представляют собой линии тока, пересекающиеся под прямым углом в начале координат, которое является критической точкой.

Так как поток все-таки направлен вдоль асимптот, то на большом расстоянии от начала координат два источника ведут себя как один источник мощности 2т, помещенный посредине между ними.

Если мы заменим линии тока Ох и Оу твердыми стенками, то формула (1) дает поток в бесконечной области, ограниченной двумя прямоугольными стенками, вытекающий через узкую щель в одной из стенок, как указано на рис. 147.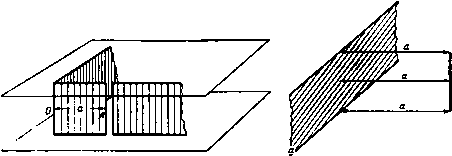

Р II с. 147.

Рис. 148.

Если в качестве твердой границы взята одна ось у, то тогда формула (1) дает поток, обусловленный источником, параллельным плоскости, ограничивающей жидкость с одной стороны, как показано на рис. 148, где, как обычно, мы предполагаем, что жидкость ограничена также параллельными плоскостями, находящимися на единичном расстоянии друг от друга.

Этот последний результат имеет большое теоретическое значение, так как он дает основы метода отображений, к изложению которого мы переходим.

8.40. Метод отображений. В предыдущем пункте мы видели, что поток, обусловленный источником мощности m в точке А (а, 0), при наличии плоскости ж = О дается формулой

w= -m 1п(г -а) -m 1п(г + а).

У

Рис. 149.

Это есть тот самый комплексный потенциал, ко-

торый мы получили бы, если бы поместили источник мощностью m в точку В {-а, 0) и представили бы себе, что жидкость имеет доступ во всю область по обе стороны от плоскости д; = 0. Если ось у является линией тока для этой системы, то плоскость можно считать удаленной. Источник мощности m в точке В называется отображением источника мощности m в точке А относительно данного плоского барьера. Это простейший случай метода отображений, который кратко можно описать следующим образом.

Предположим, что в жидкости, имеющей одну или более границ С, находится система S источников и стоков. Далее, если поместить систему S источников и стоков вне области, занятой жидкостью, и затем дать возможность жидкости иметь доступ во всю область и если при этом мы получим С как линию тока, то говорят, что система S является отображением системы S относительно границы С. В случае плоского точечного источника система состоит из единственного источника, находящегося в точке А, граница С состоит из