Наконец, для получения точки г сложим комплексные числа, представляемые точками Р и Pi, путем построения параллелограмма OPiRP. Тогда четвертая вершина параллелограмма R и есть точка г; тем самым преобразование завершается.

Пусть теперь в рассматриваемой задаче тока Р описывает окружность. Тогда точка Р' будет описывать инверсию этой окружности. Как будет показано ниже, эта инверсия является также окружностью и, следовательно, точка Pi будет описывать окружность, симметричную геометрическому месту точек Р' относительно действительной оси. Исследуем теперь геометрическое построение для нахождения геометрического места точек Pi.

7.31. Геометрическое построение преобразования. Пусть точка С - центр данной окружности, пересекающей действительную ось в точках Ан В, где ОВ = / (рис. 129).

Пусть Р -любая точка данной окружности и пусть точка Р' - ее инверсия относительно окружности радиуса / с центром в точке О, т. е.

0Р0Р' = 1* = 0В*, (1)

причем точка Р' лежит на отрезке ОР.

Пусть продолжение отрезка РО пересекает окружность в точке Q; проведем отрезок Р'С' параллельно CQ до пересечения с прямой СО в точке С. Сначала докажем, что геометрическое место точек Р' является кругом с центром в точке С

Доказательство. Так как АОВ и POQ-хорды круга, пересекающиеся в точке О, то

OPOQ = OAOB. (2)

Если разделить формулу (1) на формулу (2), то получим равенство

ОР ОВ OQ~OA

Теперь видим, что треугольники ОРС, OQC подобны, так как стороны Р'С и QC параллельны. Следовательно,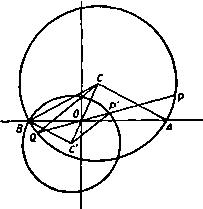

Рис. 129.

ОС CP ОР

ОС ~~ CQ ~ 0Q

ОВ OA

Таким образом, отношение ОС : ОС есть величина постоянная. Отсюда следует, что точка С-фиксированная точка.

Поскольку CQ = a есть радиус данного круга и отношение CP .CQ- константа, то отрезок CP имеет постоянную длину.

Таким образом, точка Р' описывает окружность с центром в точке С.

В силу того что 0В = 1, точка В является инверсией самой себя и, следовательно, геометрическое место точек Р' также проходит через точку В.

Так как

ОС ОВ ОС ~ OA

то треугольники ОАС и ОВС подобны и расположены подобно. Отсюда

следует, что стороны ВС и СА параллельны н поэтому

Z ABC = Z ВАС = Z Cfli4.

Таким образом, стороны ВС и ВС образуют одинаковые углы с действительной осью. Следовательно, если мы зеркально отразим окружность,

являющуюся геометрическим местом точек Р' относительно действительной оси, то мы получим такую же окружность, центр которой лежит в точке D и которая проходит через точку В (рис. 130). Это и есть искомая окружность-геометрическое место точек Pi, являющихся зеркальными отражениями точек Р'.

Так как точка В находится на линии центров CD, то две окружности должны коснуться в точке В.

Так как стороны ОС и ОС образуют одинаковые углы с осью Оу и так как отрезок 0D является зеркальным отражением отрезка ОС, то отсюда следует, что отрезки 0D и ОС образуют одинаковые углы с осью Оу. Это замечание дает нам возможность найти точку D и провести без каких-либо затруднений окружность. Теперь остается построить, согласно п. 7.30, точку R, представляющую искомое преобразование г = С+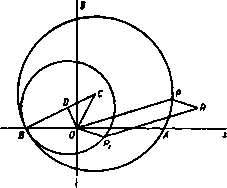

Рис. 130.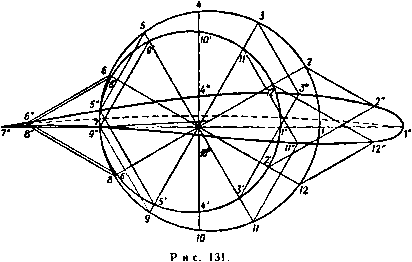

На рис. 131 показан профиль крыла, полученный путем построения радиусов-векторов через интервалы в 30°. На профиле крыла и на окружности имеется одинаковое число соответствующих точек.

Профили, полученные таким построением, известны как профили Жуковского). Они имеют затупленную переднюю кромку и острую заднюю кромку, соответствующую точке В на окружности.

>) Независимо от Н. Е. Жуковского профили этих крыльев были получены С. А. Чаплыгиным как инверсии параболы. Поэтому их иногда называют профилями Жуковского-Чаплыгина. -Лрил. перев.

7.32. Характер задней кромки крыла. Преобразование 2 = С + дает производную = ~

так что dz/d обращается в нуль в точках -I, Z = Следовательно, отображение перестает быть конформным в непосредственной окрестности этих точек. Точка С *= / находится внутри круга и преобразуется во внутреннюю точку профиля крыла. Поэтому она в дальнейшем не рассматривается. Точка / преобразуется в точку г =-21, т. е. заднюю кромку профиля. Рассматриваемое преобразование можно записать в виде

В окрестности точек С=-/ и г=-2/ положим

t /+,.e*e, 2=-2l + se% Рис. 132.

где г и S-бесконечно малые величины. Тогда можно получить приближенное равенство

и г еЧ -4/ 4/

и, следовательно,

X-f я = 2в.

Прн обходе вокруг точки В угол 0 увеличивается на я, следовательно, угол X увеличивается на 2я (рис. 132).

Отсюда следует, что обе ветви профиля крыла касаются друг друга в задней кромке, которая является поэтому геометрическим местом точек

возврата.

Обобщенный вид формулы (1), т. е.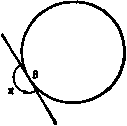

-у

р с, 133, также используется при проектировании про-

филей крыльев. Этому преобразованию соответствует класс кривых, известных под названием профилей Кармана - Треффтца. Используя те же обозначения, находим

Х + л = пв,

так что если п = 2 - Х/я, то увеличение угла 0 на я дает для угла % увеличение на 2я - X (рис. 133). Следовательно, в задней кромке две различные ветви профиля крыла теперь пересекаются под углом X.

Преобразование (2) не позволяет получить такой простой геометрической картины, которая получается при п = 2.

7.40. Постулат Жуковского). Пусть q - скорость в точке В окружности, которая преобразуется в заднюю кромку профиля крыла, ад- соответствую-шдя скорость на задней кромке. Тогда, согласно п. 6.03, можем записать соотношение

>) в отечественной литературе этот постулат называется постулатом Чаплыгина-4(укоаского, что более соответствует действительности.-/7р л. перев.

Мы видели, что иа задней кромке dz/dg = О, и, следовательно, величина q бесконечна. Этого можно избежать, если считать точку В критической точкой, т. е. в этой точке скорость = 0.

Исследование положения критических точек, проведенное в п. 7.12, показывает, что благодаря подходящему выбору интенсивности циркуляции х критические точки можно расположить в любой точке на нижней половине цилиндра, так что точку В всегда можно сделать критической точкой.

Постулат Чаплыгина - Жуковского состоит в том, что циркуляция в случае соответствующим образом спроектированного профиля всегда устанавливается такая, что точка В является критической и скорость у задней кромки профиля конечна. Это условие'), по-видимому, будет удовлетворяться

Рис. 134.

Рис. 135.

с достаточной точностью в области рабочего режима у хорошо спроектированного крыла.

Физическое происхождение циркуляции, вероятно, можно объяснить следующим образом (см. также фото 7-12).

В начале движения, т. е. прн малых скоростях воздушного потока, картина обтекания имеет обычные плавные линии тока и задняя критическая точка расположена впереди задней кромки на верхней поверхности крыла (рис. 134). Когда скорость увеличивается, даже при малой вязкости воздуха, силы вязкости возрастают и поэтому воздух перестает огибать острые края профиля, в результате чего образуется вихрь (рис. 135).

Так как в начальный момент времени циркуляция по любому замкнутому контуру, охватывающему профиль, и вихрь в рассматриваемом течении равнялись нулю, то в дальнейшем сумма циркуляции и вихря также должна оставаться равной нулю; поэтому должна существовать циркуляция вокруг профиля, равная по величине и противоположная по знаку образовавшемуся вихрю. При установившемся обтекании профиля вихрь уносится потоком, а циркуляция вокруг профиля остается.

7.45. Теорема Кутта -Жуковского*). Если неподвижный профиль крыла обтекается с циркуляцией К равномерным плоско-параллельным потоком воздуха со скоростью V в бесконечности, то на крыло действует подъемная сила, равная KqV и направленная перпендикулярно скорости V. Направление вектора подъемной силы получается поворотом вектора V на прямой угол в сторону, противоположную направлению циркуляции.

Доказательство. Так как поток воздуха равномерный и его скорость в бесконечности задана, то при достаточно больших значениях г\ имеет место следующее разложение в ряд:

.= v ..+4+4+....

>) За крылом имеется вихревой след, который является причиной того, что измеряемая циркуляция меньше, чем циркуляция, соответствующая постулату Чаплыгина-Жуковского. Влияние вихревого следа увеличивается с увеличением угла атаки.

*) В отечественной литературе эта теорема обычно называется теоремой Жуковского.-Ярил, ред.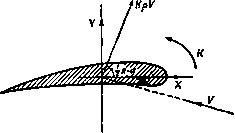

где а -угол атаки (рис. 127). Отсюда находим ш = Уе* г -/4 Inz+ - +----

Поскольку циркуляция равна К, то надо положить

-Л = . (2)

так как Inz увеличивается на 2ni при одном обходе профиля в положительном направлении. Из формул (1) и (2) получаем

(-y ,v +i-i!Hf!l .... ,3,

Если мы проинтегрируем это выражение по окружности достаточно большого радиуса, чтобы разложение (3) было справедливо, то, согласно теореме Блазиуса - Чаплыгина (см. п. 6.41), получим результнрукнцую силу

= -iKQVeo , изменив здесь / на -/, получаем

Рис. 136.

Сравнение этой формулы с рис. 136 показывает, что полученная здесь сила удовлетворяет всем условиям теоремы.

Замечания.

(I) Эта теорема была открыта Кутта в 1902 г. и независимо от него Жуковским в 1906 г. )

(II) Подъемная сила не зависит от формы профиля.

(III) Рассмотренная теория не позволяет определить лобовое сопротивление профиля, так как не учтено наличие вихревого следа и сил вязкости (см. п. 19.74).

(IV) Если крыло движется в неподвижном воздухе, то направление подъемной силы получается путем поворота вектора скорости крыла на прямой угол в направлении циркуляции.

(V) Используя теорему Блазиуса - Чаплыгина и формулу (3), легко получить следующую величину для момента силы относительно начала координат:

М = Re 2лiQBVe. (5)

7.50. Подъемная сила крыла в равномерном потоке. Преобразование Жуковского

z = Z + lVl

является частным случаем более общего преобразования следующего вида:

z = Z + f-hf+ .... (1)

Зто преобразование, примененное к окружности радиуса а с центром С в точке = s плоскости С. дает на плоскости z профиль крыла.

) Теорема доказана Кутта в 1902 г. в неопубликованной диссертации. Первая публикация принадлежит Н. Е. Жуковскому (1906 г.) (Собр. сочинений т. IV, ГТТИ, 1949 г.).- Прим. перев.

Аэродинамическая сила, действующая на крыло, обусловлена аэродинамическим давлением на элементы его поверхности. Известно, что систему сил. действующих на твердое тело (мы предполагаем, что крыло является твердым), можно заменить для любой заданной точки приведения одной силой, действующей в этой точке, и парой сил. Кроме того, величина и направление равнодействующей в точке приведения не зависит от выбора точки приведения, тогда как момент пары сил зависит от этого выбора.

Для дальнейшего исследования примем в качестве точки приведения точку С - центр окружности. Эта точка называется центром профиля: Действительное положение, которое она занимает относительно профиля, можно определить, если точки окружности и соответствующие точки профиля изобразить на одной и той же векторной диаграмме, как это, например, сделано на рис. 131. В настоящем случае мы примем точку С за начало координат. Это достигается путем замены в формуле (1) величины г на 2-f s и величины \ на

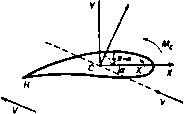(- ллоскост г - плосмст

Рис. 137.

i+ S. Тогда для достаточно больших значений С I мы получим следующий сходящийся ряд:

2 = C + f+ -+ .... (2)

Заметим также, что для уравнения (2) можно записать обратное уравнение: тогда получим

С=.-Д...=.(1--...). (3,

Последнее равенство легко проверить с любой степенью точности путем подстановки в уравнение (2).

На рис. 137 показано положение точки С на профиле и на окружности, причем эта точка является началом координат на обеих плоскостях.

Пусть а-угол атаки, тогда, согласно теореме п. 6.21, для комплексного потенциала обтекания окружности можно записать выражение

Ve% + - . Пусть окружность обтекается с циркуляцией, равной 2ях. тогда получим

a*Ve

+ ы In с.

Заменяя здесь величину С его выражением через величину г, согласно формуле преобразования, мы найдем комплексный потенциал обтекания заданного крылового профиля. ,В настоящем случае для достаточно больших значений г| мы можем применить формулы (3) и (4), тогда для

комплексного потенциала в плоскости г получим следующее выражение: + ix[\m + \n(\l--...y =

Здесь опущены члены с -j в степенях выше первой.

Сравнеиние с п. 7.45 показывает, что в данном случае

у4 = - ix, В= Ve-* a* - Ve a,. (6)

Поэтому, согласно формулам (4) и (5) п. 7.45, получим формулы

X + iY = 2я1Х(}Ке-* = 2nxQVe (7)

Mc = Re{- 2nQV*/a,e2< ). (8)

Здесь Afс -момент силы относительно центра С.

Пусть L -подъемная сила, Af-момент силы и с -хорда, тогда безразмерные величины

г г М

соответственно называются коэффициентом подъемной силы и коэффициентом момента. Коэффициент момента зависит от выбора точки, относительно которой берутся моменты.

Заметим, что подъемная сила равна произведению скорости потока в бесконечности на плотность воздуха и на циркуляцию и поэтому она не зависит от формы крыла.

7.51. Оси профиля. Начертим окружность и профиль на одной и той же векторной диаграмме; тогда прямая, соединяющая центр С с задней критической точкой на круге, называется первой осью профиля (ось I). Согласно обозначениям рис. 137, можно записать x = 2aV smfi. Таким образом, подъемная сила L пропорциональна sinP; она обращается в нуль при Р = О, т. е. когда скорость потока в бесконечности направлена по первой оси (направление CHi на рис. 137). Поэтому первую ось также называют осью нулевой подъемной силы.

С другой стороны, если в формуле (2) п. 7.50 мы положим ai= l*e, то по формуле (8) п. 7.50 получим равенство

Af с = 2nQl*V* sin (2а -f ц),

так что момент Afc обращается в нуль, если угол атаки равен-i/,p. Прямая, параллельная этому направлению потока и проходящая через центр С. называется второй осью профиля (ось II), или осью нулевого момента. Если через у обозначим угол между первой и второй осями, то

получим

Mc2nQl*V*sm (2р-2у).

7.52. Фокус профиля. Фокусом профиля называется такая точка, момент аэродинамической силы относительно которой не зависит от угла атаки.

>) А6С0.1ЮТНЫМ углом атаки иазывается угол между скоростью потока в бесконечности и осью нулевой подъемной силы.

Для доказательства существования фокуса заметим, что момент силы L относительно некоторой точки F выражается в виде

Л| = Af с-Cf cos (р - y - ф) i.

где ф -угол между прямой CF и второй осью профиля, как указано на рис. 138. Отсюда, учитывая соотношения

Мс = 2aQW sin 2 (р - v), L = AnqaV* sin p,

получаем

Mf = 2neV* {/ sin (2p - 2y)-2aCf sin p cos (p - v-ф)} =

= 2явК {/ sin (2p - 2y) - a. CF. sin (2p - y - Ф) - a Cf sin (y+Ф)}.

Это соотношение не будет зависеть от угла р-абсолютного угла атшш*), если положить

l*=aCF, 9=y.

Таким образом, доказано, что существует фокус F и что он расположен на расстоянии Р/а от центра на линии, являющейся зеркальным

отображением первой оси профиля относительно второй его оси.

Момент относительно фокуса выражается в виде

Мр--2neV i sin2Y.

Чертеж был сделан в предполо-женин, что первая ось профиля распо-Р ложена выше его второй оси в на-

правлении, указанном на рис. 138. В этом случае момент относительно фокуса отрицателен. Если, однако, вторая ось была бы выше первой, то угол y изменил бы знак и момент стал бы положительным. Относительное расположение первой и второй оси профиля соответствует, таким образом, различным динамическим свойствам профиля.

Кроме того, если y = 0, то момент Мр = 0 при любых углах атаки и поэтому вектор подъемной силы всегда проходит через фокус. В рассматриваемом случае говорят, что профиль имеет центр подъемной силы.

Для плоского крыла фокус расположен на одной четверти расстояния от центра до передней кромки крыла.

7.53. Парабола метацентров. Пусть L - линия действия подъемной силы, равной 4jiQaVsin р. Направление силы L перпендикулярно скорости потока в бесконечности. Пусть в точке Р линия действия силы L пересекает линию KF, которая проведена через фокус параллельно скорости потока в бесконечности; при этом точка К находится на первой оси профиля (рис. 139). Момент относительно фокуса F выражается в виде

Aff-fFPL-O,

отсюда, применяя теорему синусов для треугольника FKC, получаем

СП Мр \ sln2Y i гр - Fff

1~~2 Т sinp -2*7С- 2

Примеры 1да

Таким образом, геометрическое место точек Р является прямой линией, параллельной первой оси профиля, и средней линией между этой осью и фокусом F. О)гласно известному свойству параболы, основание перпендикуляра, опушенного на касательную из фокуса, лежит на касательной к параболе, проведенной в ее вершине. Отсюда следует, что линии действия подъемной силы касаются параболы, фокусом которой служит точка F, а директрисой является первая ось профиля. Эта парабола называется параболой метацентров^).

I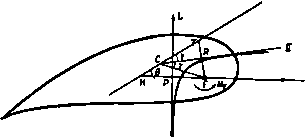

Рис. 139.

Для получения линии действия подъемной силы достаточно провести касательную к параболе метацентров перпендикулярно направлению скорости потока в бесконечности.

Вторая ось профиля касается параболы метацентров, так как если линия FRT перпендикулярна ко второй осн, то FR = RT и, следовательно, точка R лежит на касательной в вершине параболы.

Так как взаимно перпендикулярные касательные пересекаются на директрисе, то соответствующая подъаиная сила проходит через точку С, если скорость потока в бесконечности направлена по второй оси профиля.

ПРИМЕРЫ К ГЛАВЕ 7

I. Пусть профиль крыла получен преобразованием окружности, как показано в п. 7.31. Доказать, что момент сил давления относительно центра окружности равен 2ле1/* sin 2а.

2. Пусть окружность, центр которой расположен на мнимой осн, преобразуется, как показано в п. 7.31. Доказать, что получающийся при этом профиль вырождается в дугу круга, описываемую дважды; если же центр окружности лежит на действительной оси, то получается симметричный профиль.

3. Применить геометрическое построение, отвечающее простейшему преобразованию Жуковского, к следующим случаям:

а) окружность с центром в начале координат, радиус которой равен параметру / в преобразовании Жуковского;

б) окружность с центром в начале координат, радиус которой больше параметра /.

4. Рассмотреть типы преобразования, которые переводят течение идеальной жидкости прн обтекании с циркуляцией и без нее кругового цилиндра, в течение при обтекании профиля крыла. В частности, объяснить, как найти обтекание дуги круга и сечения стойки.

Какое преобразование следует применить для получения обтекания профиля заданной формы при переменном угле атаки?

5. Пользуясь обычными обозначениями для двумерного движения идеальной жидкости, определить w как функцию г для течения с проекциями скорости {U, V) при обтекании кругового цилиндра \г-го\ = Ь, если задана циркуляция / вокруг цилиндра.

Применяя преобразование

г'=г-Ьа /г,

где a - zo\ = b, -малая величина, а-действительное положитсльяое число, построить <бтекание профиля Жуковского. Путем выбора величины цнркуяяцяи получить конечное значение скорости в точке возврата.

I) Впервые парабола метацентров была введена С. А. Чаплыгиным для моноплана и М. В. Келдышем для полиплана, см. Го л у бе в В. В., Теория Крым. - Прим. перев.

е. Пусть неподвижный круговой цилиндр радиуса Ь с центром в точке (с, 0) помещен в поток, имеющий в бесконечности скорость V, направленную под углом а к оси х. Кроме того, задана циркуляция / вокруг цилиндра. Доказать, что комплексный потенциал имеет внд

w= V {(г-с)J-l- In г-c).

Применяя преобразование z=z-f о*/г, где а=Ь-с, показать, что если с мало, то преобразование дает такой же поток около крыла с симметричным профилем Жуковского. Показать, что условие конечности скорости в точке возврата имеет вид

/+4nV6sina = 0.

Отсюда иайти подъемную силу профиля.

7. Граница цилиндрического препятствия в плоскости г отображается иа окружность g = a в плоскости g с помощью преобразования

Показать, что движение жидкости вокруг препятствия дается комплексными потенциалами вида

Ф+/ф= К (e* 5+e e-* C- ) --(А/2я) In (Ш-

Доказать, что результирующая сила, действующая иа единицу длины препятствия, равна xqV, а ее момент относительно центра круга, отнесенный к единице длины, равен

2яоЬ*У* sin 2 (а+ц),

где

ej= -6 exp<2i .

8. Окружность (=а преобразуется в тонкий профиль с помощью формулы

Найти выражения комплексных величин а„ через толщину и кривизну профиля. Получить следующую формулу для подъемной силы:

L-4ncalsin(a-)-p),

и показать, что момент силы относительно центра равен

Af=2ngW sin2(a4-n),

где а-угол атаки, величины Р, 6 и ц-параметры преобразования.

9. Пусть профиль получен из окружности \Z-be*\=a с помощью следующего конформного отображения:

Предполагается, что все нули производной dz/dZ лежат внутри круга, кроме одного, расположенного иа окружности в точке J= -/= бе*-ае *; здесь о, 6 и / - действительные числа; коэффициенты а вообще говоря, считаются комплексными числами. Кроме того, пусть циркуляция вокруг профиля выбрана в соответствии с постулатом Чаплыгина-Жуковского. Показать, что иа крыло, помещенное в рассматриваемое течение, действует подъемная сила, направленная перпендикулярно к скорости в бесконечности и обращающаяся в нуль при некоторых углах атаки. Найти выражение для Of из условия, чтобы момент относительно центра круга обращался в нуль вместе с подъемной силой.

10. Преобразование г' = г-\-1*/г, где / - действительное число, переводит окружность I г4-/-вер 1=а, где а и р-действительные числа, в профиль Жуковского на плоскости г' с точкой возврата при г'=-21. Показать, что касательная в точке возврата образует угол 2fi с осью х'.

Пусть неподвижный профиль помещен в потоке несжимаемой невязкой жидкости плотности Q, комплексная скорость которого в бесконечности равна -u-\-iv=Ve. Циркуляция вокруг профиля выбрана так, что в жидкости не имеется бесконечной скорости.