Примеры 175

2. Доказать или проверить, что функция скорости

Ф = У созв

описывает потенциальное обтекание неподвижного кругового цилиндра.

При заданном давлении на бесконечности вычислить главный вектор сил, действую ших со стороны жидкости на единицу длины полуцилиндра, лежащего на плоскости, проведенной через ось цилиндра параллельно направлению потока на бесконечности.

3. Имеется плоское установившееся безвихревое течение жидкости в области, поперечное сечение которой ограничено неподвижной границей, состоящей из линий в=±л/и и кривой г cos 5в = ik*.

Пусть скорость жидкости р точке, лежащей на одной из граничных плоскостей и отстоящей на единицу длины от линии пересечения граничных плоскостей, равна V.

Доказать, что объем жидкости, проходящей за единицу времени через круговую площадку в плоскости 0 = 0, равен

4-nVo (a -bl2a c -(-8c*).

о

где а -радиус площадки, -расстояние центра площадки от точки пересечения граничных плоскостей.

4. Изобразить схематично линии тока течения, заданного комплексным потенциалом р-(ф = Лг*, и показать, что в любой точке об.1асти течения величина скорости жидкости пропорциональна расстоянию этой точки от начала координат.

5. Исследовать течение, заданное конп.1екснын потенциа.юм w-U{a*/z>), н показать, что линии тока этого течения являются лемнискатами.

В. Дан комплексный потенциал ю* = г -I. Доказать, что линией тока, на которой у^=\. является линия i/* (1-f л*) = **. Взяв эту линию за фиксированную границу течения, показать, что данный комплексный потенциал описывает обтекание этой границы равномерным потоком.

7. Пусть дано твердое тело, границы которого задаются уравнениями

(x-f 1) +у = 2, (x-l) -f , = 2.

Проверить, что потенциальное обтекание этого тела равномерным потоком, направленным на бесконечности вдоль оси у, задается функциями

Ф= -Uy

12 2 1

2(х4-1) , 2(х-1) -1

xi+yi (x+\)t+y* (x-\)*+yt J

8. Начертить линию тока, на которой ф = 0, а ф изменяется от -\-со до -оо, для двух течений:

1) г* = 4ю ,

2) z = (w-l)*/ -l-(w+l)**

Изобразить схематически вид линий тока, на которых функция ф положительна.

9. Пусть в* = 1/ (г*-Нс*). Получить уравнение линий тока в виде

yf*\Ui(xi+ci)+yi] * и* (Uix*-j-i)

ш'камть, что данный комплексный потенциал описывает обтекание бесконечным потоком тоиксго препятствия, выступающего перпендику.пярно из прямолинейной границы.

10. Применив конформное отображение z = S-f-e*/J к обтеканию цилиндра г -с пкккпсти г потоком, скорость которого равна U, получить соответствующее решение 1л ..Лтекаиия потоком той же скорости плоской области, форма которой задается ветвью припой

(х +.j/*)-fa*-f 2а (х -е (x -f / ) = 0.

Начертить *ту кривую д.1я разных значений отношения а/с и исследовать физический МЫС! мо.пучеиных результатов.

11. Пусть функция * = /(г) задает некоторое течение несжимаемой жидкости. Обо-1ИДЧИМ чер1ч p) давление в точке, в котор<)й скорость жидкости равна V. Доказать, что сгч-танлиющие (X, V) главного вектора сил давления жидкости слева от некоторой линии пта на жидкость справа от нее, приложенные к дуге АВ этой линии тока, задаются

Считать, что луч 6 = 0 направлен против скорости потока на бесконечности.

12. Применить к равномерному потоку, задаваемому комплексным потенциалом w=Uz, последовательно конфюрмные отображения

, (а+Ь)* ia , а -ЬЗ

и показать, что плоское движение в плоскости гз соответствует обтеканию неподвижного эллиптического цилиндра равномерным потоком, у которого направление скорости на бесконечности составляет угол а с большой осью эллипса. Показать также, что аргумент Zj определяет эксцентрический угол точек на эллипсе.

Доказать, что давление на поверхности эллиптического цилиндра достигает минимума в точках, у которых эксцентрический угол 6 удовлетворяет уравнению

fl tg64-6 ctga=0.

13. Пусть комплексный потенциал w = f(z), где а' = <р-}-ф и z = x-\-iy, определяет двумерное течение. Найти вид функции / для обтекания неподвижного кругового цилиндра х*+у*=а* равномерным потоком, скорость которого иа бесконечности равна по величине V и составляет угол а с осью х.

Используя конформное отображение г'~г+с*/г (с<а) или любым другим способом найти комплексный потенциал обтекания э.1Липтического цилиндра

X* и*

---4--- = 4с* ch psh2p

где Р=:1па/с, тем же потоком и вычислить момент, стремящийся повернуть цилиндр вокруг его оси.

14. Показать, что функция тока обтекания эллиптического цилиндра потоком, параллельным малой оси эллипса, имеет вид

if=-Vceb)sh (l-lo)cosn.

Здесь использованы обычные обозначения.

Пользуясь последней формулой, показать, что функция тока обтекания эллиптического цилиндра потоком, скорость которого на бесконечности q образует угол 6 с осью ОХ, имеет вид

ф = (?геЬ)5Ь a-?o)sin (Tj-B).

15. Эллиптический цилиндр 5 = go помещен в поток, скорость которого U параллельна большой оси эллипса. Доказать, что скорость q течения задается формулой

п2- гЧ±1 (S-So) + sin Ti

и что скорость достигает максимального значения U (а+Ь)1а на концах малой оси эллипса.

16. Эллиптический цилиндр обтекается потоком, у которого на бесконечности составляющие скорости вдоль большой н малой осей эллипса, образующего поперечное сечение цилиндра, равны соответственно - Vcosf и - Vsinp. Течение вокруг цилиндра обладает циркуляцией x. Найти главный вектор и главный момент сил, действующих со стороны жидкости на единицу длины цилиндра.

17. Показать, что комп.1ексный потенциал

w= -uz-ub /Й* .-(5+ )-ь'3).

где z=Vo*-b*cb (l+ir\), задает обтекание неподвижного эллиптического анлнндра с полуосями а и Ь потоком со скоростью U, направленной вдоль большой оси цилиндра;

соотношением

X + (ро + у QV ) (!/в-Уа) ] - [ i- (ро + у eV ) (хв - ха) ] =

Интеграл в правой части соотношения берется вдоль любой дуги, которая может быть непрерывно деформирована в дугу АВ без пересечения особых точек течения.

Цилиндр, радиус которого а, помещен в поток жидкости, скорость на бесконечности которого равна V, а давление ро. Показать, что главный вектор сил давления жидкости на единицу длины четверти цилиндра, вырезанной плоскостями 6-0 и в = я/2, имеет составляющие

Примеры 177

прн этом течение вокруг цилиндра имеет циркуляцию /. Найти также главный вектор сил давления жидкости на цилиндр.

18. Жидкость, плотность которой равна q, совершает безвихревое движение в области между двумя софокусными эллиптическими цилиндрами 4=а и g = p, где

ж+<,=ссЬ (6+ т1).

Доказать, что если циркуляция равна k, то кинетическая энергия слоя жидкости единичной толщины равна

19. Пусть x+iy={l-\-ii\)*. Доказать, что функция тока потенциального обтекания параболы потоком, скорость которого U параллельна оси параболы, имеет вид

Ф=21/(5-5о)т1-

20. Доказать, что комплексный потенциал 1в*=г задает течение между двумя софокусными и коаксиальными параболическими цилиндрами.

21. Однородный поток жидкости, скорость которого V направлена вдоль положительной оси X, обтекает бесконечный параболический цилиндр

/Fcos- = /5.

Доказать, что потенциал скорости этого течения имеет вид

= Vrcose-l-2V /fl/rcos-

и что главный вектор сил давления на единицу длины цилиндра равен ngaV*. Давление на бесконечности принять равным нулю.

22. Доказать, что формула

x+iy-\-c

где Jb-действительная величина, определяет безвихревое движение жидкости, циркулирующей около двух неподвижных цилиндров, причем циркуляция около одного цилиндра равна 2лк, а циркуляция около другого цилиндра равна -2nk,

Найтн течение, полученное с помощью конформного отображения

x+iy=----,

x+iy-c

где а-действите^пьная величина, а также определить границы области, в которой это течение происходит.

23. Задано обтекание цилиндрического тела радиуса а, лежащего на дне глубокого потока. Показать, что разность давлений в верхней и нижней точках тела равна a*QU*/32, где t/-скорость потока на бесконечности.

24. Используя коаксиальные координаты, проверить, что комплексный потенциал

=t/2ctg п п

определяет равномерный поток при л = 2, а прн п=1-течение около кругового цилиндра.

25. Однородная несжимаемая невязкая жидкость занимает область, ограниченную плоскостью х=0 и цилиндром (х-6)*-j-y*=a*, где 6>а. Жидкость движется со скоростью V вдоль отрицательной оси у. Доказать, что это движение описывается комплексным потенциалом

9--,tt)= .Vz--2iYfl z

1 , VI а*

=1 II (b-l-x,) (zt x )

где

z = x-f- y, Xo=b, х„=6-

b+Xn-t

Глава 7 ПРОФИЛИ КРЫЛЬЕВ

7.10. Циркуляция вокруг кругового цилиндра. Рассмотрим комплексный потенциал

где X - действительное число.

На цилиндреzI = а имеем г = ае (рис. 123). Отсюда w = -х0. так что ф = О и ф = -хв. Таким образом, цилиндр является линией тока ф = 0.

Кроме того, если мы обойдем один раз вокруг цилиндра в положительном направлении, то угол О примет значение О -- 2я и, следовательно, величина ф уменьшится на 2лх.

Таким образом, как следует из формулы (2) п. 3.71, вокруг цилиндра имеет место циркуляция величиной 2лх. В общем случае формула (1) дает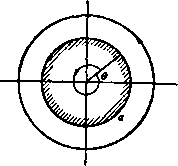

-хв, ф = х1п-.

Рис. 123.

так что циркуляция равна 2лх по каждой окружности, охватывающей один раз цилиндр (см. п. 3.71). Линиями тока являются концентрические окружности с центрами на оси цилиндра.

Определение. Если циркуляция по окружности равна 2лх, то мы будем называть х интенсивностью циркуляции.

Цель этого определения - избежать постоянного повторения множителя 2п при анализе.

В рассматриваемом случае имеем

так что X есть скорость течения на единичном расстоянии от начала координат. Формулу (1) можно представить в виде

ш=*х Inz-/х In а.

Так как добавление к потенциалу константы не оказывает никакого физического действия, то мы можем пользоваться комплексным потенциалом /х1п г. Действительно, такой вид комплексного потенциала часто оказывается более удобным, несмотря на кажущееся отсутствие согласованности в физических размерностях. В этом случае х по-прежнему является скоростью на единичном расстоянии от начала координат. Отбрасывание константы приводит к тому, что границей цилиндра становится линия тока ф = х In о вместо ф = 0.

Очень важно иметь в виду, что описываемое здесь движение жидкости происходит без вращения в том смысле, что вихрь равен нулю. В самом деле.

вихрь, вычисленный по формуле (см. п. 4.20)

,., <? <dq я ,dq к х

оказывается равным нулю.

7.11. Циркуляционное движение жидкости между концентрическими цилиндрами. Комплексный потенциал w = tx In z применим также для описания циркуляционного движения жидкости, заключенной между двумя концентрическими круговыми цилиндрами, так как функция тока ф = xin г постоянна на цилиндрах г = а, г = 6.

Циклическое движение в данном случае, а также в случае, рассмотренном в предыдущем пункте, оказывается возможным в силу того, что область, занятая жидкостью, является двусвязной (см. п. 3.70).

7.12. Обтекание кругового цилиндра с циркуляцией и без циркуляции.

Обтекание кругового цилиндра радиуса а без циркуляции задается комплексным потенциалом

0+4)-

Обтекание кругового цилиндра с циркуляцией интенсивности х задается комплексным потенциалом ix Inz/a.

Комбинируя эти движения жидкости, мы получаем следующий комплексный потенциал:

= (г + ) + х1п|. (1)

Цилиндр по-прежнему остается частью линии тока ф = 0. Действительно, полагая z=ae*e, найдем, что ш-действительная величина и, следовательно, ф= 0.

Для отыскания общей формы линий тока исследуем прежде всего критические точки, определяемые уравнением

dz или

Теперь мы должны рассмотреть три случая

X < 2aV, X = 2aV, х > 2aV.

Случай I. Если х < 2aV, то можно положить x/2aV = sinp. Тогда г - а (- sin Р ± cos Р), так что критические точки являются точками пересечения цилиндра с прямой линией, расположенной ниже центра цилиндра и проведенной параллельно действительной оси.

На рис. 124 показаны критические точки Лив, угол Р и расположение линий тока.

Воздействие циркуляции приводит к тому, что увеличивается скорость жидкости в точках, расположенных над цилиндром, н уменьшается скорость в точках, расположенных под цилиндром. Таким образом, давление над цилиндром уменьшается, а под цилиндром увеличивается, и поэтому на цилиндр будет действовать сила, направленная вверх по оси у.

Функция тока

не изменится, если вместо х напишем -дг, т, е. линии тока симметричны относительно оси у. Поэтому результирующая сила в направлении оси X равна нулю, т. е. цилиндр не испытывает лобового сопротивления.

Рис. 124.

Если циркуляция равна нулю, то критические точки лежат на оси х. Таким образом, другое воздействие циркуляции заключается в том, что эти точки передвигаются вниз.

Случай П. Пусть jt = 2aV, тогда угол Р = я/2. В этом случае критические точки совпадают в точке С (рис. 125) иа нижней половине цилиндра.

Случай III. Пусть х > 2aV, положим x/2aVechp. Тогда находим 2 = ш (-ch р ± sh Р) = -а/в±Р, Обозначая эти точки через Zi, Zg, имеем \ziZi\ = a*.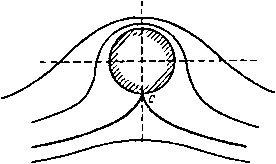

Рис. 125.

Таким образом, критические точки теперь являются точками инверсии относительно окружности на мнимой оси; одна из них находится внутри цилиндра и не принадлежит рассматриваемой области течения.

В критической точке линии тока пересекаются обязательно под прямым углом (см. п. 4.60), и, таким образом, жидкость внутри образовавшейся петли может циркулировать вокруг цилиндра, никогда не соединяясь с основным потоком (рис. 126).

Для нахождения давления в точках на цилиндре определим производную

- = V (1 е-2в)+e-ie = e-ie 2iV sin 0 -Ь Отсюда

и, следовательно,

£. + 4v. (4K.sin0-b-blfsin0).

Результирующая сил, действующих со стороны жидкости на цилиндр, имеет следующие компоненты:

2я 2я

Х= - J pcos0arf0, К=-J psin0arf0.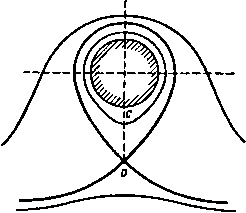

Рис. 126.

Если в выражении для давления р заменить 9 на 9 4-л, то изменится только последнее слагаемое. Следовательно, давление в диаметрально противоположных точках выражается следующим образом:

где

Pi-:esin0, pi + tQsinQ,

= + .V 2V*sin 0-g

Ясно, что слагаемые pi не оказывают никакого действия на цилиндр, так как они взаимно уничтожаются. Следовательно,

2я 2я

X = 2хVe I sin 9 cos 0 d0, К = 2xKq sin* 0 dQ,

X = 0, Кв2лхоУ.

Таким образом, на цилиндр действует сила 2nxQV, стремящаяся поднять его под прямым углом к направлению основного потока. Эту силу обычно называют подъемной силой.

Расчет подъемной силы, даже в этом очень простом случае, весьма облегчается благодаря применению теоремы Чаплыгина-Блазиуса. В рассматриваемом случае эта теорема дает следующее выражение для силы:

Здесь интеграл берется по замкнутому контуру цилиндра. Единственным полюсом подинтегральной функции внутри контура является точка z = 0.

Вычет в этой точке равен коэффициенту при ~ в подннтегральном выражении, т. е. величине 2iVx.

Отсюда по теореме Коши о вычетах находим

Х- <Г = у /Q-2я/ 2<Ух = - / 2яе^ .

так что, как и прежде, Х = 0, У = 2яхдУ.

Преимущество теоремы Чаплыгина -Блазиуса состоит в том, что в ней используется единственная переменная z, а все остальные переменные исключены с помощью теоремы о вычетах.

7.13. Равномерное течение с поперечным градиентом скорости. Пусть ось X расположена горизонтально, скажем на уровне земли, а ось у направлена вертикально вверх. Пусть распределение скоростей имеет следующий вид:

и=-щ, v = 0, ca = const, (1)

причем скорость уменьшается, когда мы приближаемся к земле; поперечный градиент скорости равен ди/ду=-ш. Этот тип распределения скоростей часто встречается при ветре в природных условиях и известен как равномерное течение с поперечным градиентом скорости. Вихрь равен dv/dx-ди/ду = (а. Таким образом, течение с поперечным градиентом скорости имеет постоянный вихрь, поэтому дадим более точное определение такого течения.

Определение. Течение с постоянным вихрем называется равномерным течением с поперечным градиентом скорости.

Для течения с постоянным вихрем ш в соответствии с формулами (6) п. 4.40 и с формулами из п. 5.33 можно получить для функции тока ф следующее уравнение:

Отсюда путем интегрирования находим

ф = /(г) + 7(г) + а)гг, (2)

причем произвольные функции f (г) и ] (г) должны быть комплексными сопряженными, поскольку ф - действительная величина. Следовательно, самое общее течение с поперечным градиентом скорости можно получить путем наложения течения с равномерным поперечным градиентом скорости, функция тока которого имеет вид фо = (1/4)сог2. и безвихревого течения, комплексный потенциал которого равен 2i7(z).

В качестве примера рассмотрим течение с циркуляцией около кругового цилиндра (см. п. 7.12). на которое накладывается течение, определяемое

функцией тока фо = (l/4)(ozz. Комплексный потенциал для безвихревого течения задается формулой п. 7.12 (1), и, следовательно, по формуле (2) получим

2/ф = К (г - г) + Ve* (у - j) + х 1пгг+ тгг.

Для нахождения силы, действующей на цилиндр, используем формулу (7) п. 6.41. На цилиндре гг - а*, или г = а*1г, следовательно,

и, таким образом, по формуле (7) п. 6.41 находим результирующую силу X - /К = - 2ie- 2я1 res (дф/аг)? о = =--2яе (х-1-<йа*)К.

Итак, подъемная сила увеличивается нз-за наличия течения с поперечным градиентом скорости, если <о/х положительно, и уменьшается, если а>/х отрицательно. Заметим, что течение с поперечным градиентом скорости создает подъемную силу даже при отсутствии циркуляции.

7.20. Профиль крыла. Крыло, используемое в современных самолетах, имеет профиль, похожий по форме на рыбу (рис. 127). Такое крыло имеет затупленную переднюю кромку и острую заднюю кромку. Проекция профиля на касательную, показанную на рнс. 127, называется хордой. Отношение размаха крыла к хорде профиля называется удлинением.

Рис. 127.

Линией кривизны профиля называется геометрическое место точек, расположенных посредине между точками, в которых ордината, перпендикулярная к хорде, пересекает крыло./Сривизмо(2 профиля является отношение максимальной ординаты линии кривизны профиля к его хорде.

Рассмотрим основы теории обтекания такого профиля крыла прн следующих предположениях:

1. Воздух ведет себя как несжимаемая невязкая жидкость.

2. Крыло представляет собой цилиндр, поперечное сечение которого является кривой вышеуказанного типа.

3. Рассматриваемое течение представляет собой двумерное безвихревое циклическое движение жидкости.

Вышеуказанные предположения являются, конечно, только приближениями к действительному состоянию вопроса. Однако эти предположения дают возможность понять основные принципы решения рассматриваемой задачи. По данному вопросу имеется значительная библиография, которую мы здесь не можем охватить даже в общих чертах. Наша цель состоит только в том, чтобы дать вводный обзор простейших сторон явления

Было установлено, что профили, полученные путем конформного преобразования круга преобразованием Жуковского (см. п. 6.30). имееют хорошую обтекаемую форму. Подъемная сила для таких профилей может быть вычислена по известной формуле для кругового цилиндра. Существуют два способа получения крыльевых профилей указанного вида.

а) Профиль крыла получается путем преобразования данной окружности.

б) Профиль крыла задан. Требуется найти окружность, которая преобразуется в заданный профиль. Естественно, что способ (б) является более сложным. Мы ограничимся исслепованием способа (а). Для этой цели рассмотрим подробнее преобразование Жуковского.

7.30. Дальнейшее исследование преобразования Жуковского. Преобразование

рассматриваемое как отображение плоскости С на плоскость г, эквивалентно последовательным преобразованиям

Если задать С и Ci, то второе из этих преобразований сводится к простому сложению на векторной диаграмме. Попытаемся теперь получить Ctt если С

задано. Положив

будем иметь

Рис. 128.

жем записать равенства

следовательно.

Рассмотрим точки Р (J) и Р, (Ci), изображенные на рис. 128.

Если мы проведем прямую Р,Р' перпендикулярно действительной оси и пересекающую ОР в точке Р'. то смо-

0Р.0Р' = 1*.

Таким образом, точка Р' является инверсией точки Р относительно центра инверсии 0. Для нахождения точки Pi мы должны сначала найти точку инверсии Р', а затем отражение отрезка ОР относительно действительной оси, тем самым мы получим точку Р,.

1) Для более подробного ознакомления см. Theoretical Aerodynamics, Lnd., 1958.

Мили-Томсон (Milne-Thomson),