случае а=с, и мы получаем комплексный потенциал обтекания пластины, наклоненной под углом а к направлению потока на бесконечности, в виде w = Uach(i - ia). Критические точки и в этом случае лежат на гиперболических ветвях линии тока (рис. 114)

т)=о, 11=л-Ьа.

На передней и задней кромках пластины скорость обращается в бесконечность, так что найденное рещение не может полностью представить реальную картину обтекания пластины.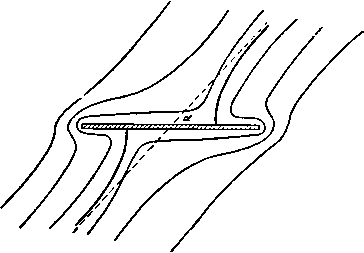

Рис. 114.

Если перейти к переменной г, то мы получим

u)=i/(zcosa -/)/г* -a*sino ).

Если пластина перпендикулярна направлению потока на бесконечности, то комплексный потенциал течения имеет вид

ш= -iUV z-a*.

6.35. Общий метод. Рассмотрим цилиндр с поперечным сечением С, помещенный в поток, комплексный потенциал которого равен Uze-*<. Аналогично тому, как были введены эллиптические координаты, введем функцию

z = f(t.), (1)

определяющую систему координат (s, г\), в которой кривая С задается уравнением 1= lo- Тогда С=2?о-С а кривой С. Таким образом, комплексный потенциал

w=F{l) + F{2lo-t) (2)

на кривой С принимает действительные значения. Следовательно, кривая С является линией тока ф = 0.

Далее, комплексный потенциал равномерного потока можно представить в виде

иге-= f/MC) = /1 (С) + (О (3)

Мы будем предполагать, что функция РгЦ) содержит лишь члены, обра-щающиеся в нуль на бесконечности. Если мы добьемся, кроме того, чтобы

функция fi(25o-С), сопряженная функции f, из последнего равенства, обращалась в нуль на бесконечности, то искомый потенциа[л обтекания будет иметь следующий вид:

w=Fi{l)+Fi(2lo-t). (4)

Так, например, для эллипса мы имеем г = с ch С. тогда из равенства (3) получаем

Следовательно,

что совпадает с равенством (1) п. 6.33.

Чтобы определить искомую систему координат, предположим, что кривая С задана в параметрическом виде уравнениями x=fi{t), y=ft{t)-Возьмем вместо параметра / переменную/(So-С) > тогда получим-соотношение

z=-h{ilo-il) + if2{ilo-il). (5)

которое обладает требуемыми свойствами.

Так, например, в случае эллипса jc=acos/, y = bsmt, и мы приходим к соотношению

2 = (о ch -6sh 6о) ch С + {Ь сЫо-а sh So) sh С.

которое после подстановки a = cchSo> 6 = cshSo переходит в известное соотношение для эллиптических координат.

Заметим, что содержание этого пункта представляет собой общий метод решения рассматриваемых задач. Частный вид выражения для системы координат, использованного здесь для иллюстрации общих положений, нисколько не ограничивает общности данного метода.

6.41. Теорема блазиуса*). Пусть неподвижный цилиндр помещен в установившееся безвихревое течение жидкости. Обозначим через X, Y

проекции главного вектора сил давления, действующих на цилиндр, на оси некоторой системы координат, а через М-главный момент этих сил относительно начала координат. Тогда, если пренебречь внешними силами, можно записать равенства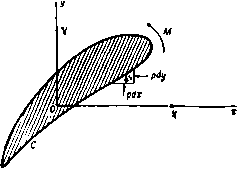

М

Рис. 115.

где ш -комплексный потенциал течения, q-плотность жидкости, а интегралы берутся вдоль контура цилиндра.

Доказательство. В точке Р на элемент дуги ds действуют силы dX = -pdy, dY=pdx, которые создают момент dM=л (jcdjc-}-у dy) (рис. 115).

1) В русской литературе эту теорему называют теоремой Чаплыгина -Блазиуса. (Эта теорема была доказана С. А. Чаплыгиным в 1910 г. независимо от Блазиуса.)- Прим. перев.

Таким образом,

d{X-iY) = -ipdl (1)

dM=Re{pzdz]. (2)

Из уравнения для давления имеем

p = a-lQ9 , (3)

где а -некоторая постоянная.

Так как постоянное давление ие дает результирующей силы, мы можем принять, что

I \ dw dw

Р= - о Q<? - --9 Q

2 W--dz а

откуда следует, что

d(X-iY)=iQdw, dM==Re{-QZ-dw} Но ф = 0 на контуре С и, следовательно, dw=dw, так что

dM = Re{-l,z(ydz}.

Проинтегрировав последние два равенства вдоль контура С, получим искомое выражение для силы и момента, что и требовалось доказать. Иногда оказывается полезным рассматривать равенство

M + iN=-i, \z(ydz,

где Л^-мнимая часть интеграла.

Если движение жидкости неустановившееся, то уравнение для давления содержит член Qd<f/dt и, следовательно, к выражениям для силы и момента мы должны добавить члены

(с) (С)

Однако на цилиндре функция ф принимает постоянное значение с{/). Следовательно,

Таким образом, в полученное выражение для X - iY и М-\ iN надо добавить соответственно члены

-iQ-wdz и Q~ J [ш+ ic {t)\zdz.

В только что сформулированной теореме Блазиуса все интегралы брались по контуру цилиндра. Этот контур может быть расширен произвольным образом, если только он не охватывает прн этом новых особых точек подинтегральной функции. В гидродинамике такие особые точки встречаются в тех случаях, когда в жидкости имеются источники и стрки. Однако с этими явлениями мы будем иметь дело позже, а теперь рассмотрим несколько простых примеров на применение теоремы к различным случаям обтекания тел.

Следовательно,

Пусть цилиндр движется с постоянной скоростью в покоящейся жидкости. Тогда силы можно вычислять по теореме Блазиуса, так как динамические условия не изменяются, если на это движение наложить постоянную скорость, равную и противоположно направленную скорости цилиндра. При этом цилиндр будет находиться в покое, а жидкость будет обтекать цилиндр.

Мы можем, кроме того, получить формулы для силы и момента, выраженные через функцию ф, которая существует, если данное движение жидкости вихревое. В самом деле, с помощью формулы (1) п. 5.33 мы получаем

- -(4) Следовательно, положив в выражении (3) а = 0, находим

pdz=-2Qdz. (5)

Но ф=ф(г, 2) -постоянна на контуре С, поэтому

-dz+-dz=0 на контуре С. (6)

Комбинируя равенства (I), (2), (5) и (6), мы находим равенства

X-iY=-211 Г ydz, MRe{2Q]z(ydz}. (7)

(с) (с)

Далее, заметим, что хотя ф зависит от г и г, на контуре С переменная Z является функцией г, и, следовательно, после исключения г в равенствах (7) мы можем использовать теорему о вычетах и теорему об изменении контура интегрирования.

6.42. Действие равномерного потока на эллиптический цилиндр. Возвращаясь к п. 6.23, мы видим, что комплексный потенциал обтекания эллиптического цилиндра имеет вид

ш=ЫсЬ(С -Ы; z = cchC,

где

cA = U{a + b), Со = ;о + /а.

Силу и момент, действующие иа цилиндр, можно вычислить по теореме Блазиуса. Мы имеем

=-§ = = 4*t.-b£..j) .

При вычислении силы и момента мы будем брать интегралы по окружности, охватывающей цилиндр, радиус которой настолько велик, что функция dw/dz может быть разложена в сходящийся ряд по степеням 1/z. Тогда интеграл по замкнутому контуру будет содержать только коэффициенты при членах 1/z разложения подинтегрального выражения (п. 5.57).

В нашем случае

Отсюда получаем X - iY = 0 или Х=0, К=0, а

M + iN--1Q. 2ш- (- cM e-t sh Со) = Qc** (1 - e-2U) =

= iJiQcM* 11 - e-2U (cos 2a -1 sin 2a)J.

Следовательно, M = - nQcAe- sin a cos a. Далее, из п. 6.33 получим равенство

с* \fl-b J

M = - nQ (a* - fr*) (/* sin a cos a.

Знак минус означает, что на цилиндр действует пара сил, которая стремится поставить его поперек потока. Из рис. 113 видно, откуда появляется эта пара сил: критические точки, или точки максимума давления, расположены на контуре несимметрично.

Полученный результат является характерным для любого продолговатого тела, помещенного в поток. В частности, он дает объяснение поведения лодки, дрейфующей по течению.

Заметим, что момент пары сил обращается в нуль, если а = 6. т. е. в случае кругового цилиндра. Этого можно было ожидать заранее.

Момент пары сил обращается в нуль также и при а = О, т. е. в случае, если большая ось эллипса параллельна потоку на бесконечности. Небольшое отклонение от такой ориентации большой оси вызывает возмущающую пару сил, момент которой будет возрастать до тех пор, пока а не станет равным я/4. Таким образом, эллиптический цилиндр с большой осью, параллельной направлению потока на бесконечности, неустойчив. Это явление хорошо иллюстрируется на примере корабля, который требует постоянного внимания рулевого для поддержания заданного курса.

Пара сил обращается в нуль, когда а=я/2, т. е. когда цилиндр расположен поперек потока. Однако это положение цилиндра устойчиво, так как отклонение от него вызывает восстанавливающую пару сил, момент которой возрастает с отклонением.

6.50. Коаксиальные координаты. Возьмем точки Л и Б с координатами соответственно (с, 0) и ( - с, 0). Выберем ось х за начало отсчета углов, а точки Л и Б в качестве полюсов. Тогда координатами произвольной точки Р будут соответственно {г^, в,) и (гг, Oj). Числа г, и г, называются биполярными координатами точки Р (рис. 116).

Если точка Р описывает некоторую окружность, проходящую через точки 4 и В, то ЛРВ = 01 - 02 остается постоянным. Такие окружности образуют коаксиальное семейство. Семейство окру ж- Рис. 116. ностей, ортогональное к указанному, имеет

точки i4 и В предельными точками. Когда точка Р описывает некоторую окружность этого семейства, величина Гг/л остается постоянной.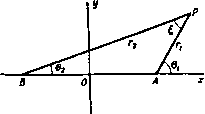

Введем обозначения

5=9,-91, ti = In.

тогда

таким образом.

Т)- ig = In (Г,в*в ) - In (Г|в*в1),

г+с г-с

Если положить С=5+Л. то из последнего равенства следует

г-с

Положение точки Р определено, если мы знаем, в каком квадранте она находится, и известны постоянные S и т) на окружностях, проходящих через эту точку. Таким образом, мы можем назвать величины I, г\, определяемые формулой (1), коаксиальными координатами *) аналогично тому,

как мы ввели эллиптические координаты.

Из равенства (1) мы получим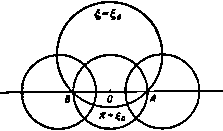

tj-comt

Рис. 117.

так что

z = /cctgyC- (2)

Это равенство аналогично выражению, определяющему эллиптические координаты.

Кривая I = const является окружностью с центром в точке (О, ctgS) и радиусом, равным ccosecg. Кривая т) = const является окружностью с центром в точке (с cthr), 0) и радиусом, равным cchr\. Так как г= -/cctgViC, то мы находим

Т= Т (*=*8Т Y О' 7 (tgj С+ctg 1С ).

Но так как имеет место равенство

2 sin у CsinyC = cosiT) -cosi = chTi -cosS,

то мы заключаем, что

X shT) у sing

c~chT-cos с chtj-cos

На действительной оси 1=0, за исключением точек, расположенных между А и В, для которых = я.

Заметим, что £ < я, когда у>0. Кроме того, если 1=1о на дуге окружности, проходящей через точки А и В, для которой у>0. то на дуге той же самой окружности, для которой у<0, =1о + л (рис. 117).

Если точка Р уходит в бесконечность, то прямые РА и РВ стремятся стать параллельными, причем РА=РВ. Таким образом, г]->Опри Р->со, а 1->0 или g -> 2я соответственно для у>0 и у <0.

В заключение заметим, что в точках А н В величина т) обращается в бесконечность.

1) Эти координаты называют также биполярными координатами.-Прим. перев.

6.51. Обтекание впадины или выступа дна. Комплексный потенциал a =i/ctg. z=/cctglc,

где п-действительная величина, описывает течение с линией тока ф = 0,

соответствующей 6=0 или 1=пл, так как в обоих случаях функция w

принимает действительные значения.

Таким образом, функция w описывает обтекание границы, которая состоит из дуги окружности, проходящей через точки Л и В, на которой i = Vtnn, и части оси х, лежащей вне этой дуги (рис. 118).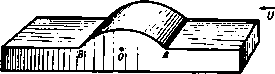

Рис. 118.

Для определения скорости течения мы имеем формулу

sin у С

dm dm dt 4 j

sin-

Ha бесконечности 1-*0 и u - iv -U, т. е. н% бесконечности имеется однородный поток. Далее,

1Ы/ /sin -2 М / ch-cos6

sin I-sin 4

ch --COS-

Когда мы подходим к точке А, ц->оо; в этом случае имеет место приближенное равенство

- 16У 2(1-4)ч

Таким образом, если л<2, то ->0, а если л>2, то 9-*оо, когда

ц - оо.

Если п < 2, то мы имеем обтекание выступа дна, причем скорость жидкости во всех точках конечна. В частности, если п = 1, мы имеем обтекание выступа, образованного полуокружностью, и задача становится аналогичной задаче обтекания кругового цилиндра (см. п. 6.22).

Если п = 3, то мы имеем обтекание впадины на дне, образованной половиной окружности, причем в точках А и В скорость обращается в бесконечность. На дне этой впадины т) = О, g = Зя/2. Следовательно, скорость в этой точке равна */JU.

Отметим также, что при п < 2 найденный комплексный потенциал описывает обтекание цилиндра, поперечное сечение которого состоит из двух

равных круговых сегментов, построенных на общем отрезке, так как это течение симметрично относительно общего отрезка сегментов.

На рис. 119 показаны два таких поперечных сечения. Круговой цилиндр является частным случаем этих цилиндров.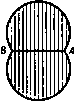

Рис. 119.

Если мы наложим на течение однородный поток со скоростью и {w= -Uz), направленной слева направо, то получим комплексный потенциал

u>=i/ctg- i/icctg-C,

который описывает течение жидкости при движении цилиндра с заданным поперечным сечением в направлении ВА со скоростью U. Комплексный потенциал

w= ~ f/cosactg sinacosec-

задает обтекание описанных выше твердых тел потоком со скоростью на бесконечности, равной (-f/cosa, -i/sina). В самом деле, при = :t: пя/2

величина w обращается в действительную функцию, при этом ф=0. С другой стороны, при С->0 имеем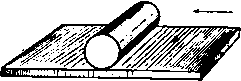

dw dz

>-U COS а-fit/ sin a.

6.52. Обтекание цилиндрического Рис. 120. тела. Потенциал обтекания выступа

на дне, полученный в предыдущем пункте, может быть использован для описания обтекания цилиндрического тела, лежащего на дне, если устремить точку А к точке В (рис. 120).

Радиус а окружности, дуга АВ которой стягивает угол I, определяется равенством

20=.

sin g

в случае выступа 1 - пл/2 и, следовательно.

sin-

z = i с ctg у С. .= MLctgl.

(2) (3)

Теперь если точку А устремить к точке В, то с-*0. Тогда из формулы (1) следует, что п->0, а из формулы (2) следует, что С-*0.

Поэтому можно предположить, что величина с является малой, и равенства (I) и (2) записать в виде

2с , 2ic

Подставив эти равенства в формулу (3), мы получим комплексный потенциал обтекания цилиндрического тела радиуса а, лежащего на дне, в следующем виде:

W = ianU ctg -ij - anU cth .

Этот результат можно проверить следующим образом. Из формулы

а,= Ф+1> = алг/с1Ь(--), г*=х* + у'

видно, что функция W принимает действительные значения при у = О, т.е. линия у = 0 является линией тока ф=0. Функция w принимает действительные значения также и при алу/г*= л/2.

Таким образом, линия тока z состоит из действительной оси у=0 и окружности х* + у* = 2ау.

Далее, заметим, что при больших значениях \г\ комплексный потенциал имеет вид

w = anU-=Uz. ал

Следовательно, на бесконечности комплексный потенциал w определяет однородный поток, параллельный действительной оси и направленный слева направо.

Скорость жидкости можно вычислить следующим образом:

t dwdi .гиг^!-!--!-

г

а*я*и*Г 2 12

а*п*и* Г

. /ал , ал \ . f ал ая \

7Г

2алд; 2ал1/ ch-j--cos-

На поверхности цилиндра г*=2ау и. следовательно.

/ 2 \ . , . 2алх

а*л*и* 4,.ch.

На плоскости у = 0 к, следовательно,

. а*л*и*

6.53. Цилиндр в тоннеле. Если положить

ГО ф= - Хб. ф=-хп. Функция ф обращается в постоянную на линии 1)= const. Функция ф уменьшается на 2лх, если мы обойдем окружность П= const. Из формулы (2) п. 3.71 следует, что комплексный потенциал w

представляет собой течение жидкости с циркуляцией *) 2пх вокруг цилинд ра Т1 = Л1> окруженного цилиндром г\ = г\г (цилиндр в тоннеле, рис. 121). Исключив переменную С. мы получим

2=- cctg-, tt;=2xarcctg-, dw 2х(с

dz z*-c* г -с г-\-с

Таким образом, по теореме Блазиуса, сила, действующая на внутрен НИИ цилиндр, равна

I 2.1

.v-,r.-S,.

L {г-о* (z-c) (г+с)+ (г+с)* J

d2 =

Спедовательно.

т. е. главный вектор сил давления жидкости на внутренний цилиндр стре мится увеличить расстояние между осью цилиндра и осью тоннеля.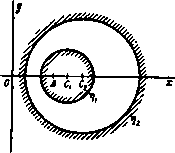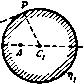

Рис. 121.

Рис. 122.

Интересно отметить один частный случай, когда радиус окружности tit становится бесконечным, т. е. когда эта окружность вырождается в мнимую ось (рис. 122). В этом случае мы имеем обтекание цилиндра, ось которого параллельна стенке. На цилиндр действует сила, равная nv?Qlc, которая стремится прижать цилиндр к стенке.

Так как А является предельной точкой, то, проведя касательную, мы получим

с =0Л = ОР =ОСГ-а = Л -а ,

где /{ - расстояние оси цилиндра до стенки, а -радиус цилиндра. Следовательно, сила, действующая на цилиндр, равна

ях*£

ПРИМЕРЫ К ГЛАВЕ 6

I. Неподвижный круговой диск обтекается однородным потенциальным потоком /килкости. Скорость потока иа бесконечности и постоянна по направлению, но изменяется по величине. Показать, что сила, которую необходимо приложить к диску, чтобы удержать его в покое, равна 2m{du/dt), где т -масса жидкости, вытесненная диском.

М Заметим что область является двусвязной (п. 3.70).