Линии тока этого течения симметричны относительно оси у, так как вид уравнений линий тока ие изменяется при изменении знака переменной X. Из соображений симметрии следует, что линии тока, лежащие над осью х, получаются отражением относительно этой оси линий тока, лежащих под осью х.

Если изменить направление скорости U на обратное, то картина течения не изменится.

Если положить ф = Ша, то уравнения линий тока примут вид

Легко видеть, что y->ka при г-*оо, следовательно, прямые у^ка являются асимптотами линий тока. Кроме того, если > О, то у > ka, т. е. линии тока приближаются к своим асимптотам сверху.

С другой стороны, рассмотрим линии тока, асимптоты которых задаются уравнениями

y = ka, у-(Л-Ь1)а.

Пусть у, и уа -координаты точек пересечения этих линий с осью х=:0. Тогда

(* + 1)а-й(1-;).

Если из первого равенства вычесть второе, то после преобразований мы найдем, что

У2-У1 ytSi

Так как правая часть этого равенства положительна и больше единицы, то мы заключаем, что у%>yi и уг - у^Ка. Но на бесконечности расстояние между этими линиями равно а. Следовательно, проходя около цилиндра, линии тока сближаются. Так как через каждое сечение трубки тока должна проходить одна и та же масса жидкости, то скорость жидкости на данной линии тока около цилиндра больше, чем скорость на бесконечности, и вследствие теоремы Бернулли давление меньше давления на бесконечности, если отсутствуют внешние силы.

в.23. Разветвляющаяся линия тока. При обтекании цилиндра контур цилиндра должен быть частью линии тока. Так как функция тока имеет вид

Ф=г/у(1-;).

то мы заключаем, что контур цилиндра г = а соответствует отрезку линии тока ф = 0. Полная линия тока ф = 0 состоит, следовательно, из линий у = 0 и г = с, т. е. окружности г^а и той части оси x, которая лежит вне этой окружности (рис. 106).

Таким образом, эта линия тока идет к цилиндру вдоль оси X, пока ие достигает точки L цилиндра, затем разветвляется и идет в противоположных направлениях вдоль контура цилиндра, далее соединяется снова в точке М и вновь идет вдоль оси х.

Рассматриваемая линия тока называется разветвляющейся линией тока. Знание положения этой линии тока сразу дает нам возможность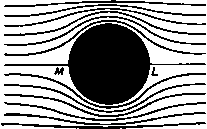

Рис. 106.

или

p-n = 4-Q(l-4sin*e).

\ / Мы можем представить это рас-

пределенне давления на полярной ди- аграмме, на которой давление в каж-

дой точке измеряется длиной отрезка. Рис. 107. отложенного на радиусе, проведенном

через данную точку. Прн этом давление на бесконечности П измеряется длиной радиуса цилиндра а. В этом случае мы видим (рис. 108), что в точках Л^ Л^а. Ni, Ni, полярные углы О которых равны 30, 150, 210, 330°, давление равно П. На дугах NiLNf и NfMNf давление превосходит величину П, причем максимум избыточного давления равен VaQf и достигается в точках L и М. На дугах NxANt и NtBNi давление меньше П, и максимум отрицательного избыточного давления равен /zQU* и достигается в точках А н В. Диаграмма давления симметрична, давления в точках с полярными углами О и О 4-л равны, так что равнодействующая гидродинамических сил

качественно нарисовать картину течения, если мы проведем последовательные линии тока, сначала близкие по форме к разветвляющейся линии, а затем все менее и менее искривленные. Изображенная на рис. 106 картина течения поясняет приведенные рассуждения.

Критическая точка определяется из уравнения dw/dz -О, которое в данном случае имеет вид

Следовательно, критическими являются точки с координатами г -а и 2=-а, т. е. точки I и Af, в которых разветвляющаяся линия тока встречает цилиндр. Мы видим, что в соответствии с общими свойствами пересекающихся линий тока (см. п. 4.60) точки L и М являются двойными точками, в которых касательные к линиям тока пересекаются под прямым углом.

6.24. Распределение давления на цилиндре. Для вычисления скорости в точке 2 = аев на цилиндре мы имеем соотношение

g = £/(l-f)=£/(l - е-2*в) = . 2U sin 0.

Следовательно,

9-2£/sine. (1)

Таким образом, величина д* достигает максимума при в=±я/2; скорость в этих точках равна 2U, т. е. удвоенной скорости течения на бесконечности.

Итак, скорость имеет наибольшую величину в точках А п В, в которых диаметр, перпендикулярный направлению течения на бесконечности, пересекает контур цилиндра (рис. 107).

Из формулы (1) следует также, Что скорость в точке Р на цилиндре пропорциональна площади треугольника LPM.

Если обозначить через П давление на бесконечности, то для величины гидродинамического давления в точке на поверхности цилиндра теорема . Бернулли дает нам следующее вы-

-Д.. ражение:

/ 4-b2f/ sin e = ?

давления, действующих на цилиндр, равна нулю. Эти результаты согласуются с экспериментом только на передней части цилиндра NiLNi] на остальных частях поверхности цилиндра действительные давления, вообще говоря, меньше приведенного на диаграмме.

и

Рис. 108.

6.25. Кавитация. Обычно полагают, что жидкость не способна выдерживать отрицательное давление. При относительном движении твердой границы и жидкости последняя соприкасается всюду с границей только до тех пор, пока давление в каждой точке на границе остается положительным. Так, в точке, где давление обращается в нуль, дальнейшее небольшое уменьшение давления сделало бы давление отрицательным и должен был бы образоваться вакуум. Образование вакуумных полостей в жидкости называется кавитацией. Это явление часто встречается; например, его можно наблюдать около концов быстро вращающихся лопастей пропеллера.

При обтекании цилиндра кавитация может наступить в том случае, когда давление обращается в нуль в тех точках, где оно минимально, т. е. в точках А и В (В = ± я/2). Условие для этого выражается равен-<:твом

- 3 е

Если скорость и превышает эту величину, то в точках А н В на поверхности цилиндра возникает кавитация.

6.29. Применение конформного отображения. Рассмотрим конформное отображение плоскости J на комплексную плоскость г с помощью функции

z = /(a (1)

Пусть при этом область R, внешняя по отношению к контуру С в плоскости С. переходит в область S, внешнюю по отношению к контуру А в плоскости г. Тогда контур С переходит в контур А (рис. 109).

Пусть течение жидкости в области R плоскости С задается комплексным потенциалом

а (С) = ш=ф-Ь<ф. (2)

Тогда в соответствующих точках Сиг, связанных соотношением (1), функция W и, следовательно, функции ф и ф имеют те же значения.

Далее, контур С является границей и вследствие этого линией тока течения в плоскости С- Следовательно, ф=)&= const во всех точках

контура С. Так как точки контура А отображаются в точки контура С, то = k ьа всех точках контура А. Следовательно, контур А является линией тока течения, определяемого в плоскости г функциями (1) и (2).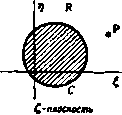

2-плоскость

Рис. 109.

Явный вид комплексного потенциала в плоскости г можно было бы получить путем исключения С из формул (1) и (2), ио часто предпочтительнее рассматривать J в качестве параметра и воздерживаться от исключения. Так, например, для определения скорости в точке Q плоскости г. соответствующей точке Р плоскости мы имеем равенство

Следовательно,

dwd dzddi-

UQ-tVQ = -

Up-iVp

Пусть через и 9, обозначены скорости венно. Тогда имеет место равенство

в точках Р н Q соответст-

Пусть через dSi и dS, обозначены соответствующие элементы площади в точках Р н Q. Так как отображение конформно, то мы знаем, что элементы d5, и dSj подобны и что отношение соответствующих длин в элементах dSt и dS, равно Id/dz]. Таким образом.

dSi dS.:

и, следовательно.

9?dS,= 9 dS

отсюда следует равенство

н котором интегралы берутся по соответствующим площадям. Но эти интегралы измеряют кинетическую энергию жидкости, занимающей соответствующие площади. Таким образом, кинетическая энергия в обоих движениях одна и та же.

Теперь мы видим применение конформного отображения в гидродинамике. Если мы знаем комплексный потенциал движения жидкости, заданный выражением (2), и если мы затем отобразим плоскость С на плоскость г с помощью функции (1), то получим комплексный потенциал движения жидкости в плоскости Z. При этом границами движения в плоскости г будут линии, связанные выражением (1) с границами движения в плоскости С-Линии тока в одной плоскости переходят в линии тока в другой плоскости, а скорости в соответствующих точках связаны равенством (3).

6.30. преобразование Жуковского. Преобразование

является одним из самых простых и наиболее важных преобразовании двумерных течений жидкости. С помощью этого преобразования мы можем отобразить плоскость Z на плоскость z и наоборот.

Мы начнем с замечания, что при больших значениях \\г\ мы имеем приближенное равенство Z=z, так что окрестности бесконечно удаленных точек обеих плоскостей переходят друг в друга без изменений. Таким

Z мосяост

Рве 110.

образом, однородный поток на бесконечности в плоскости г соответствует однородному потоку того же направления и той же скорости в плоскости Z.

Теперь рассмотрим, как преобразуется окружность с центром в начале координат в плоскости Z при преобразовании Жуковского.

Сначала заметим, что точкам L, М в плоскости Z с координатами Z = Va с, Z = - 4t с соответствуют точки S, Н в плоскости г с координатами z = c, z = -с (рис. 110).

Пусть точка Р' плоскости z соответствует точке Р, лежащей на окружности \Z\ = 4i (а + Ь) в плоскости Z; предположим, что а*-6 = с*. Тогда преобразование Жуковского дает нам следующие равенства:

Z + -c = z-c, Z + -\-c = z + c.

PS = \z-c\ =

PH=\z + c\ =

2PL

a + b

и. следовательно.

SP+PH.

2(PL +PM ) a+b

Ho так как OP является медианой треугольника MPL, то PL*+PM* = 2(0L* + 0P%

и. следовательно,

SP + HP = 2a,

откуда следует, что точка Р' описывает эллипс, фокусы которого находятся в точках S к Н, а большая ось равна 2а.

Далее, если обозначить через В конец малой полуоси этого эллипса, а через С -его центр, то можно написать равенство

CB* = SB*-CS*b*.

Следовательно, полуоси эллипса равны соответственно а н Ь.

Итак, концентрические окружности с центрами в начале координат в плоскости Z отображаются в софокусные эллипсы в плоскости z.

В частности, если мы возьмем 6 = 0, то окружность Z=Vaa перейдет*) в прямую линию SH, соединяющую фокусы, так как малая полуось соответствующего эллипса равна нулю и а = с.

Этот результат легко получить и аналитически. Для любой точки на окружности Z = Va оеу следовательно, z = Va с^*® + Va ое-* = а cos 0.

Zплоскости

г-плоскость

Рис. 111.

Отсюда следует, что когда угол 0 принимает значения О, я/2, я, % я, 2я, Z принимает значения а, О, -а, О, а; когда точка Р описывает полуокружность LDM, точка Р' описывает прямую SH, а когда точка Р завершает окружность, описывая дугу MEL, точка Р' движется в обратном направлении по прямой HS (рис. 111).

Теперь рассмотрим обратное преобразование, при котором Z задается в зависимости от г. Из формулы (1) получаем

Z -zZ-fc =0,

Знак плюс перед квадратным корнем означает, что должна быть взята та ветвь функции Yz - c*, которая действительна и положительна, когда точка Z находится на действительной положительной оси вне эллипса. Когда величина z велика, из формулы (2) получаем приближенные равенства Z = z или Z=0 в зависимости от того, положительный или отрицательный знак берется перед корнем. Следовательно, если мы выберем знак плюс перед корнем, то функция (2) будет отображать точку, внешнюю по отношению к эллипсу в плоскости 2, на точку, внешнюю по отношению к окружности в плоскости Z.

Следовательно, преобразование

Z = 4-(2 + K?). с = а -6

отображает внешность эллипса с полуосями а н Ь в плоскости г на внешность окружности радиуса Va(a + 6) в плоскости Z.

) В нашем случае dzldZ=-Q в точках L и М. Следовательно, мы должны предположить, что окружность стремится к этим точкам в смысле п. 5.63.

6.31. Обтекание эллиптического цилиндра. Согласно п. 6.22, комплексный потенциал обтекания цилиндра в плоскости Z потоком, скорость которого на бесконечности равна U и направлена под углом а к оси х, имеет вид

,= i/(z.- +<).

Внешность круга отображается на внешность эллипса в плоскости г с полуосями а н Ь, центром в начале координат и осью а, направленной вдоль оси X, с помощью преобразования

Z={z + Vz), c* = a*-b*.

Следовательно, комплексный потенциал обтекания эллиптического цилиндра имеет вид

Но так как

w = -U{a + b)

то окончательное решение задачи имеет вид

а+Ь т- J

Однако это выражение для комплексного потенциала неудобно для детального исследования картины течения. Чтобы упростить его, мы введем эллиптические координаты.

6.32. Эллиптические координаты. Пусть

г=ссЬС. (1)

где

Тогда

x + iy==cc\\{l + It]) = с ch S cos т) -f- /с sh i sin т), откуда следует, что

дг = с ch g cos т), y = cshisinT) (2)

и. следовательно.

= 1. (3)

.= 1. (4)

ccosSt) c*sin*t)

Из уравнения (3) видно, что если I имеет постоянное значение 1о. то точка с координатами (д:, у) лежит на эллипсе, большая и малая полуоси которого а и b равны соответственно

а=сс\\1о, 6 = csho. (5)

и, следовательно.

Эллипсы, соответствующие постоянным значениям') I, образуют семейство софокусных эллипсов, расстояние между фокусами которых

М В дальнейшем мы будем предполагать, что каждому значению 5о соответствует некоторый эллипс, и буд.:м считать, что О .< <с , 0< т|<я Можно было бы считать, что >0 для у>0 и 1<0 для у<0. Тогда соответствующие неравенства имели бы яд со<К+сг., 0<Л> т-

равно 2с. Кривые (4), соответствующие постоянным значениям т), являются гиперболами, софокусными друг с другом и с эллипсами.

Далее, через любую точку плоскости мы можем провести два конических софокусных сечения, одно из которых является эллипсом, а другое-гиперболой. На эллипсе величина \ сохраняет постоянное значение, а на гиперболе -величина ц. Если мы знаем эти значения и ц, то мы можем провести конические сечения, а их пересечение фиксирует нам точку. Поэтому параметры \ л х\ называются эллиптическими координатами.

Рассмотрим подробнее эллипс Из формулы (3) мы видим, что т)

является эксцентрическим углом точки (х, у) на эллипсе. Геометрический

смысл сказанного ясен из рис. 112.

На этом рисунке АА является главной осыо эллипса = , а точки S и Н являются его фокусами. На рис. 112 показана также софокусная гипербола, пересекающая эллипс в точке Р. На АА, как на диаметре, построена вспомогательная окружность. Ордината PN пересекает эту окружность в точке Q. Угол Q ON = г\.

Полуоси эллипса суть а и Ь, поэтому сравнение выражений (2) и (5) показывает, что т) есть эксцентрический угол точки Р. Но

JC = ОЛ = СХ? cos QON = а cos QON,

и, следовательно, имеет место необходимый результат.

Мы можем теперь видеть, что если т) = т)о на ветви гиперболы, лежащей в первом квадранте, то на ветвях той же самой гиперболы, лежащих во втором, третьем и четвертом квадрантах, г\ принимает значения соответственно я -т)о, я-Ьцо, 2я -т)о.

Из формулы (4) видно также, что прямая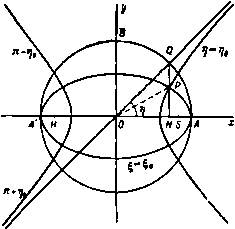

Рис. 112.

JL..

tgri.

является асимптотой для гиперболы, проходящей через точку Р. Эта асимптота совпадает с радиусом 0Q.

Чтобы закончить описание эллипса S = lo. рассмотрим уравнения (5). Складывая и вычитая эти уравнения, получаем равенства

a-Hfr = c(cho + sh 1о) = свЧ

а -ft=c(cho -sh o)=< ~* -

Разделив первое равенство (6) на второе, найдем, что

а+Ь

а - Ь

И. следовательно.

а+Ь а - Ь

Это равенство определяет параметр 1о в зависимости от полуосей эллипса а и Ь.

Наконец, заметим, что фокусы (с, 0), { - с, 0) соответствуют значениям geO. Т1=0 и 1 = 0, т) = я. Это непосредственно следует из формул (2).

6.33. Применение эллиптических координат к изучению обтекания эллипса. Комплексный потенциал обтекания эллипса был найден в п. 6.31. Если мы положим z = cchC. то получим Vz-c* =cshC и отсюда найдем равенства

г 4-i/iTZ = с (ch С + sh С) = cet,

г-yrZt* = с (ch C-sh I) = ce-i.

Кроме того, из формулы (6) п. 6.32 следует, что на эллипсе = So имеют место соотношения

а+ 6 = се* , а - Ь = се-.

Следовательно.

или

w=U{a+b)ch{i-lo-ia)- (1)

Мы получили выражение для комплексного потенциала обтекания эллипса в эллиптических координатах.

Если положить S=lo. то получим соотношение

w= и (а +Ь) ch i -а) = и (а + Ь) cos (т) -о).

т. е. ф=0. Таким образом, эллипс 1=1о образует часть линии тока ф=0. которая является, следовательно, разветвляющейся линией тока.

Из равенства (1) следует, что функция тока имеет вид

ф = i/ (а + 6) sh (£- lo) sin (т)-о).

Отсюда следует, что вся разветвляющаяся линия тока задается уравнениями

sh(i-i,)=0 и sin(T)-o)=0. т. е. уравнениями

S=b . 1==о, Ti=o-fn.

Последние значения г\ соответствуют ветвям гиперболы, конфокальной с эллипсом, и, следовательно, пересекающей эллипс под прямым углом.

Линия, параллельная направлению потока на бесконечности и проходящая через точку О, явля- Рис. из.

ется асимптотой к этой гиперболе.

Общий вид линий тока исследуемого течения показан на рис. ПЗ. Асимптота для разветвляющейся линии тока проведена штриховой линией. Разветвляющаяся линия тока пересекает эллипс в точках М и L, которые являются, следовательно, критическими точками. В этих точках М н L на поверхности эллиптического цилиндра действует пара сил, стремящаяся поставить цилиндр поперек потока. Мы вычислим величину этой пары сил в п. 6.42.

Для определения скорости мы имеем формулу

аж <<; U(a+b)sb(Z - lo-ia) it ~ dl йг ~ cshC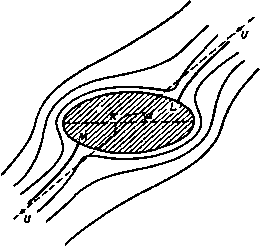

И, следовательно, в критических точках

С -1о -0=0 или in,

откуда следует, что равенства 6 = 5о. г\ = а или а + я дают нам точки L и М, найденные уже из уравнения разветвляющейся линии тока. Кроме того.

f/(a-f- )sh(S-&,-/a) Ща \-b)sh(t~l,+ia)

и*(а-{-Ь)* ch (С+ё - ago) - ch (£ - ё- 2 Д) ch(;-ft)-ch(C-C)

* (Д + *) сЬ2(6-Ь))- со52(л-а) о -ft ch2g-cos2ti

t/ (o-i-b) shMS-b,) + sin(Tl-a) a-b sh J+sin Tj

Так как S = О только в фокусе эллипса, отсюда следует, что знаменатель последнего выражения не может обращаться в нуль и. следовательно, скорость жидкости нигде не обращается в бесконечность.

Распределение давления по поверхности эллиптического цилиндра находится по уравнению Бернулли, которое имеет следующий вид:

р . 1 иЦа^Ь) l-cos2(n-a) П , \ ,

е 2 а~Ь ch2b,-cos24 Q 2

где через П обозначено давление на бесконечности. Условие dp/dr\=0 дает соотношение для определения точек, в которых давление достигает максимума и минимума, а именно

sin 2 (п - а) ch 21о- sin 2т) + sin 2а = О,

или

sin - а) (cos (tj - а) ch 25 -cos (ij + a)) = 0.

Корни уравнения stn(T) -a) = 0 определяют координаты точек, в которых давление максимально. Точки, в которых давление минимально, находятся, следовательно, из уравнения

Отсюда с использованием результатов п. 6.32 получаем

Если через Р обозначить точку, определяемую этим уравнением, то последний результат означает, что касательная к поверхности эллипса в точке Р параллельна нормали к поверхности в критической точке.

Если значение tgii= - 6 /a*clga подставить в уравнение (2), то после некоторых преобразований получим величину минимального давления

n + lef/ [l-(a4-6) ( + )J. Условие отсутствия кавитации, следовательно, имеет вид

6.34. Обтекание пластины. Если положить fc=0. то рассматриваемый эллипс выродится в линию, соединяющую фокусы эллипса So = 0- В этом